A Spatial Pattern Extraction and Recognition Toolbox Supporting Machine Learning Applications on Large Hydroclimatic Datasets
Abstract
:1. Introduction
2. Method
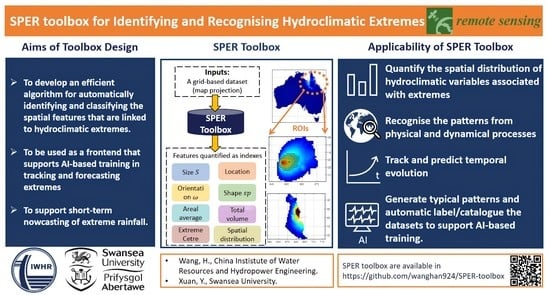
2.1. The Design of the SPER Toolbox
2.2. Thresholding Segmentation and Boundary Detection
2.3. The Algorithm for Extracting and Quantifying the Spatial Features of the ROI
2.4. The Algorithm for Quantifying the Physical Features of the ROI
3. Results
3.1. Illustrative Case 1: Catchment-Orientated Extreme Rainfall Variation in England and Wales
3.2. Illustrative Case 2: Pattern Recognition of Daily Rainfall over the Last Century in Great Britain
3.3. Illustrative Case 3: Tracing Rainfall Area and Spatial Distribution in 24 h in Guangdong, China
4. Discussion
4.1. Potential Use as the Frontend of Supporting AI-Based Training
4.2. Limitations and Recommendations to Further Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bárdossy, A.; Filiz, F. Identification of flood producing atmospheric circulation patterns. J. Hydrol. 2005, 313, 48–57. [Google Scholar] [CrossRef]
- Montanari, A. Hydrology of the Po River: Looking for changing patterns in river discharge. Hydrol. Earth Syst. Sci. 2012, 16, 3739–3747. [Google Scholar] [CrossRef] [Green Version]
- Shaharudin, S.; Ahmad, N.; Zainuddin, N.; Mohamed, N. Identification of rainfall patterns on hydrological simulation using robust principal component analysis. Indones. J. Electr. Eng. Comput. Sci. 2018, 11, 1162–1167. [Google Scholar] [CrossRef]
- Rinaldi, A.; Djuraidah, A.; Wigena, A.H.; Mangku, I.W.; Gunawan, D. Identification of Extreme Rainfall Pattern Using Extremogram in West Java. IOP Conf. Ser. Earth Environ. Sci. 2018, 187, 012064. [Google Scholar] [CrossRef]
- Panu, U.S.; Unny, T.; Ragade, R. A feature prediction model in synthetic hydrology based on concepts of pattern recognition. Water Resour. Res. 1978, 14, 335–344. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Qiu, M.; Zhao, P.; Zhang, K.; Huang, J.; Shi, X.; Wang, X.; Chu, W. A short-term rainfall prediction model using multi-task convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017. [Google Scholar] [CrossRef]
- O’Gorman, P.A.; Dwyer, J.G. Using machine learning to parameterize moist convection: Potential for modeling of climate, climate change, and extreme events. J. Adv. Model. Earth Syst. 2018, 10, 2548–2563. [Google Scholar] [CrossRef] [Green Version]
- Gentine, P.; Pritchard, M.; Rasp, S.; Reinaudi, G.; Yacalis, G. Could machine learning break the convection parameterization deadlock? Geophys. Res. Lett. 2018, 45, 5742–5751. [Google Scholar] [CrossRef]
- Petersik, P.J.; Dijkstra, H.A. Probabilistic Forecasting of El Niño Using Neural Network Models. Geophys. Res. Lett. 2020, 47, e2019GL086423. [Google Scholar] [CrossRef]
- Liu, Y.; Racah, E.; Correa, J.; Khosrowshahi, A.; Lavers, D.; Kunkel, K.; Wehner, M.; Collins, W. Application of deep convolutional neural networks for detecting extreme weather in climate datasets. arXiv 2016, arXiv:1605.01156. [Google Scholar]
- Nayak, M.A.; Ghosh, S. Prediction of extreme rainfall event using weather pattern recognition and support vector machine classifier. Theor. Appl. Climatol. 2013, 114, 583–603. [Google Scholar] [CrossRef]
- Nguyen-Le, D.; Yamada, T.J. Using weather pattern recognition to classify and predict summertime heavy rainfall occurrence over the Upper Nan river basin, northwestern Thailand. Weather Forecast. 2019, 34, 345–360. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Hassanzadeh, P.; Pasha, S. Predicting clustered weather patterns: A test case for applications of convolutional neural networks to spatio-temporal climate data. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Hally, D. Calculation of the Moments of Polygons. 1987. Available online: https://apps.dtic.mil/sti/citations/ADA183444 (accessed on 4 August 2022).
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Pham, D.T.; Dimov, S.S.; Nguyen, C.D. Selection of K in K-means clustering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 103–119. [Google Scholar] [CrossRef] [Green Version]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat.-Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Morissette, L.; Chartier, S. The k-means clustering technique: General considerations and implementation in Mathematica. Tutor. Quant. Methods Psychol. 2013, 9, 15–24. [Google Scholar] [CrossRef] [Green Version]
- Ochoa-Rodriguez, S.; Wang, L.P.; Gires, A.; Pina, R.D.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; van Assel, J. Impact of spatial and temporal resolution of rainfall inputs on urban hydrodynamic modelling outputs: A multi-catchment investigation. J. Hydrol. 2015, 531, 389–407. [Google Scholar] [CrossRef]
- Anquetin, S.; Braud, I.; Vannier, O.; Viallet, P.; Boudevillain, B.; Creutin, J.-D.; Manus, C. Sensitivity of the hydrological response to the variability of rainfall fields and soils for the Gard 2002 flash-flood event. J. Hydrol. 2010, 394, 134–147. [Google Scholar] [CrossRef]
- Sangati, M.; Borga, M.; Rabuffetti, D.; Bechini, R. Influence of rainfall and soil properties spatial aggregation on extreme flash flood response modelling: An evaluation based on the Sesia river basin, North Western Italy. Adv. Water Resour. 2009, 32, 1090–1106. [Google Scholar] [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation using 3620 flood events. Hydrol. Earth Syst. Sci. 2014, 18, 575–594. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Xuan, Y. Spatial variation of catchment-oriented extreme rainfall in England and Wales. Atmos. Res. 2022, 266, 105968. [Google Scholar] [CrossRef]
- Tanguy, M.; Dixon, H.; Prosdocimi, I.; Morris, D.G.; Keller, V.D.J. Gridded Estimates of Daily and Monthly Areal Rainfall for the United Kingdom (1890–2015) [CEH-GEAR]. NERC Environmental Information Data Centre. 2016. Available online: https://catalogue.ceh.ac.uk/documents/33604ea0-c238-4488-813d-0ad9ab7c51ca (accessed on 4 August 2022). [CrossRef]
- Kirono, D.G.; Chiew, F.H.; Kent, D.M. Identification of best predictors for forecasting seasonal rainfall and runoff in Australia. Hydrol Process. 2010, 24, 1237–1247. [Google Scholar] [CrossRef]
- Muthusamy, M.; Schellart, A.; Tait, S.; Heuvelink, G. Geostatistical upscaling of rain gauge data to support uncertainty analysis of lumped urban hydrological models. Hydrol. Earth Syst. Sci. 2017, 21, 1077–1091. [Google Scholar] [CrossRef] [Green Version]
- Sohn, B.; Han, H.-J.; Seo, E.-K. Validation of satellite-based high-resolution rainfall products over the Korean Peninsula using data from a dense rain gauge network. J. Appl. Meteorol. Climatol. 2010, 49, 701–714. [Google Scholar] [CrossRef]
- Salio, P.; Hobouchian, M.P.; Skabar, Y.G.; Vila, D. Evaluation of high-resolution satellite precipitation estimates over southern South America using a dense rain gauge network. Atmos. Res. 2015, 163, 146–161. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Zhu, D.; Xuan, Y.; Cluckie, I. Hydrological appraisal of operational weather radar rainfall estimates in the context of different modelling structures. Hydrol. Earth Syst. Sci. 2014, 18, 257–272. [Google Scholar] [CrossRef] [Green Version]
- Sokol, Z.; Szturc, J.; Orellana-Alvear, J.; Popová, J.; Jurczyk, A.; Célleri, R. The role of weather radar in rainfall estimation and its application in meteorological and hydrological modelling—A Review. Remote Sens. 2021, 13, 351. [Google Scholar] [CrossRef]
- He, T.; Einfalt, T.; Zhang, J.; Hua, J.; Cai, Y. New Algorithm for Rain Cell Identification and Tracking in Rainfall Event Analysis. Atmosphere 2019, 10, 532. [Google Scholar] [CrossRef] [Green Version]
- Schultz, M.; Betancourt, C.; Gong, B.; Kleinert, F.; Langguth, M.; Leufen, L.; Mozaffari, A.; Stadtler, S. Can deep learning beat numerical weather prediction? Philos. Trans. R. Soc. A 2021, 379, 20200097. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Cho, D.; Yoo, C.; Im, J.; Cha, D.H. Comparative assessment of various machine learning-based bias correction methods for numerical weather prediction model forecasts of extreme air temperatures in urban areas. Earth Space Sci. 2020, 7, e2019EA000740. [Google Scholar] [CrossRef] [Green Version]
- Salomonson, V.V.; Barnes, W.L.; Maymon, P.W.; Montgomery, H.E.; Ostrow, H. MODIS: Advanced facility instrument for studies of the Earth as a system. IEEE Trans. Geosci. Remote Sens. 1989, 27, 145–153. [Google Scholar] [CrossRef]
- Bergemann, M.; Jakob, C.; Lane, T.P. Global Detection and Analysis of Coastline-Associated Rainfall Using an Objective Pattern Recognition Technique. J. Clim. 2015, 28, 7225–7236. [Google Scholar] [CrossRef] [Green Version]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Van Esesn, B.C.; Awwal, A.A.S.; Asari, V.K. The history began from alexnet: A comprehensive survey on deep learning approaches. arXiv 2018, arXiv:180301164. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Pedamonti, D. Comparison of non-linear activation functions for deep neural networks on MNIST classification task. arXiv 2018, arXiv:180402763. [Google Scholar]







| Location | |||
|---|---|---|---|
| England |  : 1.5~2.0 : 45°~75° |  : 1.0~1.6 : −75°~−45° |  : 1.2~2.0 : −45°~−15° |
| Wales |  : 1.0~1.2 : −15°~15° |  : 1.0~1.2 : 15°~45° |  : 1.0~1.4 : 15°~45° |
| Scotland |  : 1.0~1.5 : −75°~−15° |  : 1.0~1.5 : −75°~−15° |  : 1.2~1.6 : −30°~0° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Xuan, Y. A Spatial Pattern Extraction and Recognition Toolbox Supporting Machine Learning Applications on Large Hydroclimatic Datasets. Remote Sens. 2022, 14, 3823. https://doi.org/10.3390/rs14153823
Wang H, Xuan Y. A Spatial Pattern Extraction and Recognition Toolbox Supporting Machine Learning Applications on Large Hydroclimatic Datasets. Remote Sensing. 2022; 14(15):3823. https://doi.org/10.3390/rs14153823
Chicago/Turabian StyleWang, Han, and Yunqing Xuan. 2022. "A Spatial Pattern Extraction and Recognition Toolbox Supporting Machine Learning Applications on Large Hydroclimatic Datasets" Remote Sensing 14, no. 15: 3823. https://doi.org/10.3390/rs14153823
APA StyleWang, H., & Xuan, Y. (2022). A Spatial Pattern Extraction and Recognition Toolbox Supporting Machine Learning Applications on Large Hydroclimatic Datasets. Remote Sensing, 14(15), 3823. https://doi.org/10.3390/rs14153823