Reliability of Gridded Precipitation Products for Water Management Studies: The Case of the Ankavia River Basin in Madagascar
Abstract
:1. Introduction
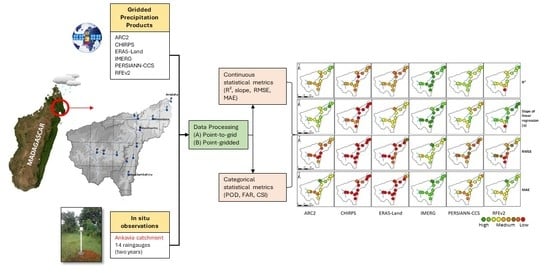
2. Materials and Methods
2.1. Study Area
2.2. Ground-Based Precipitation Data
2.3. Gridded Precipitation Products
2.3.1. ARC2
2.3.2. CHIRPS
2.3.3. ERA5
2.3.4. IMERG
2.3.5. PERSIANN
| Dataset | Full Name | Spatial Resolution | Timescale (Highest Resolution) | Period of Availability | Reference |
|---|---|---|---|---|---|
| ARC2 | African Rainfall Climatology version 2 | 0.10° | Daily | 1983–Present | [45] |
| CHIRPS | Climate Hazards Group Infrared Precipitation with station data | 0.05° | Daily | 1981–Present | [47] |
| ERA5 | ECMWF Reanalysis version 5 on global land surface | 0.10° | Hourly | 1979–Present | [50] |
| IMERG | Integrated Multi-satellitE Retrievals for Global Precipitation Measurement | 0.10° | Half-hourly | 2000–Present | [53] |
| PERSIANN | Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks—Cloud Classification System | 0.04° | Hourly | 2003–Present | [55] |
| RFEv2 | Climate Prediction Center (CPC) African Rainfall Estimates version 2 | 0.10° | Daily | 2001–Present | [57] |
2.3.6. RFEv2
2.4. Data Comparison Methodology
2.4.1. Data Quality Control
2.4.2. Data Processing
2.4.3. Rainfall Event Definition and Properties
2.4.4. Metrics for Accuracy Assessment
3. Results
3.1. Overall GPP Performance at Daily Time-Scale
3.2. GPP Performance at Daily Time Scale across the Watershed
3.3. Daily Rainfall Probability Distribution Function
3.4. Precipitation Detection Ability
3.5. Different Time Scales Assessment (Hourly to Yearly)
3.6. Event Scale Assessment
4. Discussion
5. Conclusions
- The point gridded approach is better suited than the point-to-grid approach in terms of continuous statistical metrics to evaluate gridded precipitation products against rain gauge data;
- At a daily scale, IMERG outperforms all other tested gridded precipitation products, followed by RFEv2 and ARC2;
- GPPs tend to overestimate the 0–0.2 mm/day rainfall class but underestimate the >0.2 mm/day ranges. Only GPPs with smaller grid sizes (0.04°, 0.05°) accurately estimate the >150 mm/day precipitation class;
- IMERG is shown to perform well in detecting rain events up to 100 mm/day but is surpassed by PERSIANN in detecting rain events larger than 150 mm/day. Nevertheless, a substantial proportion of rainy days are not correctly estimated by IMERG;
- IMERG shows good performance at monthly, daily, and event time scales in our case study; nevertheless, its capacity to reproduce spatial variability of rainfall is very subpar at the catchment scale.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Burton, J. Integrated Water Resources Management on a Basin Level: A Training Manual; UNESCO; Éditions MultiMondes: Paris, France; Sainte-Foy, QC, Canada, 2003; ISBN 978-92-9220-003-9. [Google Scholar]
- WMO. Tropical Hydrology; Operational Hydrology: Geneva, Switzerland, 1987; Volume 25, pp. 16–22. Available online: https://library.wmo.int/doc_num.php?explnum_id=1688 (accessed on 10 August 2020).
- Dai, Q.; Bray, M.; Zhuo, L.; Islam, T.; Han, D. A Scheme for Rain Gauge Network Design Based on Remotely Sensed Rainfall Measurements. J. Hydrometeorol. 2017, 18, 363–379. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Yilmaz, A.G.; Muttil, N. Optimal Design of Rain Gauge Network in the Middle Yarra River Catchment, Australia. Hydrol. Process. 2015, 29, 2582–2599. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Love, T.B.; Kumar, V.; Xie, P.; Thiaw, W. P5. 4 A 20-Year Daily Africa Precipitation Climatology Using Satellite and Gauge Data. In Proceedings of the 14th Conference on Applied Climatology, Seattle, WA, USA, 12–16 January 2004. [Google Scholar]
- Gosset, M.; Viarre, J.; Quantin, G.; Alcoba, M. Evaluation of Several Rainfall Products Used for Hydrological Applications over West Africa Using Two High-Resolution Gauge Networks. Q. J. R. Meteorol. Soc. 2013, 139, 923–940. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Roy, T.; Weedon, G.P.; Pappenberger, F.; Van Dijk, A.I.; Huffman, G.J.; Adler, R.F.; Wood, E.F. Daily Evaluation of 26 Precipitation Datasets Using Stage-IV Gauge-Radar Data for the CONUS. Hydrol. Earth Syst. Sci. 2019, 23, 207–224. [Google Scholar] [CrossRef]
- Bonsor, H. A Review of Continent Scale Hydrological Datasets Available for Africa; British Geological Survey: Nottingham, UK, 2010; 28p. [Google Scholar]
- Dahri, Z.H.; Ludwig, F.; Moors, E.; Ahmad, S.; Ahmad, B.; Shoaib, M.; Ali, I.; Iqbal, M.S.; Pomee, M.S.; Mangrio, A.G. Spatio-Temporal Evaluation of Gridded Precipitation Products for the High-Altitude Indus Basin. Int. J. Climatol. 2021, 41, 4283–4306. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A Quasi-Global Precipitation Time Series for Drought Monitoring: U.S. Geological Survey Data Series 832; U.S. Geological Survey: Sioux Falls, SD, USA, 2014; 4p.
- Khan, S.; Maggioni, V. Assessment of Level-3 Gridded Global Precipitation Mission (GPM) Products Over Oceans. Remote Sens. 2019, 11, 255. [Google Scholar] [CrossRef]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K. Developing Intensity-Duration-Frequency (IDF) Curves From Satellite-Based Precipitation: Methodology and Evaluation. Water Resour. Res. 2018, 54, 7752–7766. [Google Scholar] [CrossRef]
- Maggioni, V.; Massari, C. On the Performance of Satellite Precipitation Products in Riverine Flood Modeling: A Review. J. Hydrol. 2018, 558, 214–224. [Google Scholar] [CrossRef]
- Camberlin, P.; Barraud, G.; Bigot, S.; Dewitte, O.; Imwangana, F.M.; Mateso, J.-C.M.; Martiny, N.; Monsieurs, E.; Moron, V.; Pellarin, T.; et al. Evaluation of Remotely Sensed Rainfall Products over Central Africa. Q. J. R. Meteorol. Soc. 2019, 145, 2115–2138. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzambwa, S.; Ceccato, P.; Connor, S.J.; Ropelewski, C.F. Validation of High-Resolution Satellite Rainfall Products over Complex Terrain. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- van Genderen, J.L. Advances in Environmental Remote Sensing: Sensors, Algorithms, and Applications. Int. J. Digit. Earth 2011, 4, 446–447. [Google Scholar] [CrossRef]
- Hossain, F.; Anagnostou, E.N. A Two-Dimensional Satellite Rainfall Error Model. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1511–1522. [Google Scholar] [CrossRef]
- Dezfuli, A.K.; Ichoku, C.M.; Huffman, G.J.; Mohr, K.I.; Selker, J.S.; van de Giesen, N.; Hochreutener, R.; Annor, F.O. Validation of IMERG Precipitation in Africa. J. Hydrometeor. 2017, 18, 2817–2825. [Google Scholar] [CrossRef] [PubMed]
- Adeyewa, Z.D.; Nakamura, K. Validation of TRMM Radar Rainfall Data over Major Climatic Regions in Africa. J. Appl. Meteorol. 2003, 42, 331–347. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; Levizzani, V.; Roo, A.D. Validation of Satellite-Based Precipitation Products over Sparsely Gauged African River Basins. J. Hydrometeorol. 2012, 13, 1760–1783. [Google Scholar] [CrossRef]
- Asadullah, A.; McINTYRE, N.; Kigobe, M. Evaluation of Five Satellite Products for Estimation of Rainfall over Uganda/Evaluation de Cinq Produits Satellitaires Pour l’estimation Des Précipitations En Ouganda. Hydrol. Sci. J. 2008, 53, 1137–1150. [Google Scholar] [CrossRef]
- Yeh, H.-C.; Chen, Y.-C.; Chang, C.-H.; Ho, C.-H.; Wei, C. Rainfall Network Optimization Using Radar and Entropy. Entropy 2017, 19, 553. [Google Scholar] [CrossRef]
- Ageet, S.; Fink, A.H.; Maranan, M.; Diem, J.E.; Hartter, J.; Ssali, A.L.; Ayabagabo, P. Validation of Satellite Rainfall Estimates over Equatorial East Africa. J. Hydrometeorol. 2021, 23, 129–151. [Google Scholar] [CrossRef]
- Van Soesbergen, A.; Mulligan, M. Uncertainty in Data for Hydrological Ecosystem Services Modelling: Potential Implications for Estimating Services and Beneficiaries for the CAZ Madagascar. Ecosyst. Serv. 2018, 33, 175–186. [Google Scholar] [CrossRef]
- Atiah, W.A.; Amekudzi, L.K.; Aryee, J.N.A.; Preko, K.; Danuor, S.K. Validation of Satellite and Merged Rainfall Data over Ghana, West Africa. Atmosphere 2020, 11, 859. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS Satellite Rainfall Estimates over Eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale Issues in Hydrological Modelling: A Review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Desbureaux, S.; Damania, R. Rain, Forests and Farmers: Evidence of Drought Induced Deforestation in Madagascar and Its Consequences for Biodiversity Conservation. Biol. Conserv. 2018, 221, 357–364. [Google Scholar] [CrossRef]
- Tadross, M.; Randriamarolaza, L.; Rabefitia, Z.; Zheng, K.Y. Climate Change in Madagascar; Recent Past and Future; World Bank: Washington, DC, USA, 2008; p. 18. [Google Scholar]
- Rabefitia, Z.; Randriamarolaza, L.Y.A.; Rakotondrafara, M.L.; Tadross, M.; Yip, Z.K. Le Changement Climatique à Madagascar; Direction Générale de la Météorologie: Antananarivo, Madagascar, 2008.
- Gay-des-Combes, J.M.; Robroek, B.J.M.; Hervé, D.; Guillaume, T.; Pistocchi, C.; Mills, R.T.E.; Buttler, A. Slash-and-Burn Agriculture and Tropical Cyclone Activity in Madagascar: Implication for Soil Fertility Dynamics and Corn Performance. Agric. Ecosyst. Environ. 2017, 239, 207–218. [Google Scholar] [CrossRef]
- Styger, E.; Rakotondramasy, H.M.; Pfeffer, M.J.; Fernandes, E.C.M.; Bates, D.M. Influence of Slash-and-Burn Farming Practices on Fallow Succession and Land Degradation in the Rainforest Region of Madagascar. Agric. Ecosyst. Environ. 2007, 119, 257–269. [Google Scholar] [CrossRef]
- Otto, F.E.; Zachariah, M.; Wolski, P.; Pinto, I.; Barimalala, R.; Nhamtumbo, B.; Bonnet, R.; Vautard, R.; Philip, S.; Kew, S. Climate Change Increased Rainfall Associated with Tropical Cyclones Hitting Highly Vulnerable Communities in Madagascar, Mozambique & Malawi. 2022. Available online: http://www.indiaenvironmentportal.org.in/files/file/climate_change_rainfall_madagascar.pdf (accessed on 2 April 2021).
- AFD Madagascar—Rural Drinking Water Supply and Sanitation Programme—Appraisal Report. 2005. 75. Available online: https://www.afdb.org/fileadmin/uploads/afdb/Documents/Project-and-Operations/MG-2005-138-EN-ADF-BD-WP-MADAGASCAR-RURAL-WATER-SUPPLY-AND-SANITATION-PROGRAMME.PDF (accessed on 23 July 2021).
- Rasolofomanana, L.H. Vilatily&Vulnerability of Water Resources in Madagascar. Available online: https://www.pseau.org/outils/ouvrages/wateraid_vitality_and_vulnerability_of_water_ressources_in_madagascar_2016_en.pdf (accessed on 11 March 2022).
- Macron, C.; Richard, Y.; Garot, T.; Bessafi, M.; Pohl, B.; Ratiarison, A.; Razafindrabe, A. Intraseasonal Rainfall Variability over Madagascar. Mon. Wea. Rev. 2016, 144, 1877–1885. [Google Scholar] [CrossRef]
- Mc Nally, A.; Verdin, K.; Harrison, L.; Getirana, A.; Jacob, J.; Shukla, S.; Arsenault, K.; Peters–Lidard, C.; Verdin, J. P Acute Water-Scarcity Monitoring for Africa. Water 2019, 11, 168, 1968. [Google Scholar]
- Chaperon, C.; Danloux, J.; Ferry, L. (Eds.) Fleuves et Rivières de Madagascar; Monographies Hydrologiques ORSTOM; Office de la Recherche Scientifique et Technique Outre-mer: Paris, France, 1974; ISBN 978-2-7099-0344-8.
- CREAM Monographie de La Région SAVA. 2013. Available online: http://www.monographiemada.com/ (accessed on 23 July 2021).
- Aldegheri, M. Rivers and Streams on Madagascar. In Biogeography and Ecology in Madagascar; Springer: Berlin/Heidelberg, Germany, 1972; pp. 261–310. [Google Scholar]
- UPDR. Monographie de La SAVA. 2003, 115. Available online: http://www.gem-madagascar.com/sites/default/files/Sava.pdf (accessed on 5 August 2021).
- CPGU Atlas de La Vulnérabilité Sectorielle de La Région SAVA. 2012. Available online: https://drmims.sadc.int/fr/documents/database/atlas-de-la-vulnerabilite-sectorielle-de-la-region-sava (accessed on 5 August 2021).
- Novella, N.S.; Thiaw, W.M. African Rainfall Climatology Version 2 for Famine Early Warning Systems. J. Appl. Meteorol. Climatol. 2013, 52, 588–606. [Google Scholar] [CrossRef]
- Peterson, P.; Funk, C.C.; Husak, G.J.; Pedreros, D.H.; Landsfeld, M.; Verdin, J.P.; Shukla, S. The Climate Hazards Group InfraRed Precipitation (CHIRP) with Stations (CHIRPS): Development and Validation. AGUFM 2013, 2013, 150066. [Google Scholar]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The Climate Hazards Infrared Precipitation with Stations—a New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Emmanouil, S.; Langousis, A.; Nikolopoulos, E.I.; Anagnostou, E.N. An ERA-5 Derived CONUS-Wide High-Resolution Precipitation Dataset Based on a Refined Parametric Statistical Downscaling Framework. Water Resour. Res. 2021, 57, e2020WR029548. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Z.; Yan, S.; Peng, J. Do ERA5 and ERA5-Land Precipitation Estimates Outperform Satellite-Based Precipitation Products? A Comprehensive Comparison between State-of-the-Art Model-Based and Satellite-Based Precipitation Products over Mainland China. J. Hydrol. 2022, 605, 127353. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H. ERA5-Land: A State-of-the-Art Global Reanalysis Dataset for Land Applications. Earth Syst. Sci. Data Dis. 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Sabater, M. ERA5-Land Hourly Data from 1950 to Present. In Copernicus Climate Change Service (C3S) Climate Data Store (CDS); 2019; Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.e2161bac?tab=overview (accessed on 7 July 2022). [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-SatellitE Retrievals for GPM (IMERG) Technical Documentation. NASA/GSFC Code 2020, 612, 83. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J. Integrated Multi-Satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement; Springer: Berlin/Heidelberg, Germany, 2020; pp. 343–353. [Google Scholar]
- Sungmin, O.; Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG Early, Late, and Final Rainfall Estimates Using WegenerNet Gauge Data in Southeastern Austria. Hydrol. Earth Syst. Sci. 2017, 21, 6559–6572. [Google Scholar]
- Hong, Y.; Hsu, K.; Sorooshian, S. Precipitation Estimation from Remotely Sensed Imagery Using an Artificial Neural Network Cloud Classification System. J. Appl. Meteor 2004, 43, 1834–1853. [Google Scholar] [CrossRef]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Thorstensen, A.R. The PERSIANN Family of Global Satellite Precipitation Data: A Review and Evaluation of Products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef]
- Herman, A.; Kumar, V.B.; Arkin, P.A.; Kousky, J.V. Objectively Determined 10-Day African Rainfall Estimates Created for Famine Early Warning Systems. Int. J. Remote Sens. 1997, 18, 2147–2159. [Google Scholar] [CrossRef]
- Molina-Sanchis, I.; Lázaro, R.; Arnau Rosalén, E.; Calvo Cases, A. Rainfall Timing and Runoff: The Influence of the Criterion for Rain Event Separation. J. Hydrol. Hydromech. 2016, 64, 226–236. [Google Scholar] [CrossRef]
- da S.Freitas, E.; Coelho, V.H.R.; Xuan, Y.; de C.D.Melo, D.; Gadelha, A.N.; Santos, E.A.; de O.Galvão, C.; Ramos Filho, G.M.; Barbosa, L.R.; Huffman, G.J.; et al. The Performance of the IMERG Satellite-Based Product in Identifying Sub-Daily Rainfall Events and Their Properties. J. Hydrol. 2020, 589, 125128. [Google Scholar] [CrossRef]
- Rozante, J.R.; Gutierrez, E.R.; de Almeida FernandesCenter, A.; Vila, D.A. Performance of Precipitation Products Obtained from Combinations of Satellite and Surface Observations. Int. J. Remote Sens. 2020, 41, 7585–7604. [Google Scholar] [CrossRef]
- Gebere, S.; Alamirew, T.; Merkel, B.; Melesse, A. Performance of High Resolution Satellite Rainfall Products over Data Scarce Parts of Eastern Ethiopia. Remote Sens. 2015, 7, 11639–11663. [Google Scholar] [CrossRef]
- Mayor, Y.; Tereshchenko, I.; Fonseca-Hernández, M.; Pantoja, D.; Montes, J. Evaluation of Error in IMERG Precipitation Estimates under Different Topographic Conditions and Temporal Scales over Mexico. Remote Sens. 2017, 9, 503. [Google Scholar] [CrossRef]
- Veloria, A.; Perez, G.J.; Tapang, G.; Comiso, J. Improved Rainfall Data in the Philippines through Concurrent Use of GPM IMERG and Ground-Based Measurements. Remote Sens. 2021, 13, 2859. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Aryastana, P.; Liu, G.-R.; Huang, W.-R. Assessment of Satellite Precipitation Product Estimates over Bali Island. Atmos. Res. 2020, 244, 105032. [Google Scholar] [CrossRef]
- Tian, F.; Hou, S.; Yang, L.; Hu, H.; Hou, A. How Does the Evaluation of the GPM IMERG Rainfall Product Depend on Gauge Density and Rainfall Intensity? J. Hydrometeorol. 2018, 19, 339–349. [Google Scholar] [CrossRef]
- Sahlu, D.; Nikolopoulos, E.I.; Moges, S.A.; Anagnostou, E.N.; Hailu, D. First Evaluation of the Day-1 IMERG over the Upper Blue Nile Basin. J. Hydrometeorol. 2016, 17, 2875–2882. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Mohammed, S.A.; Hamouda, M.A.; Mohamed, M.M. Impact of Topography and Rainfall Intensity on the Accuracy of IMERG Precipitation Estimates in an Arid Region. Remote Sens. 2021, 13, 13. [Google Scholar] [CrossRef]
- Tan, M.L.; Duan, Z. Assessment of GPM and TRMM Precipitation Products over Singapore. Remote Sens. 2017, 9, 720. [Google Scholar] [CrossRef]
- Wang, W.; Lu, H.; Zhao, T.; Jiang, L.; Shi, J. Evaluation and Comparison of Daily Rainfall From Latest GPM and TRMM Products Over the Mekong River Basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2540–2549. [Google Scholar] [CrossRef]
- Tan, M.L.; Santo, H. Comparison of GPM IMERG, TMPA 3B42 and PERSIANN-CDR Satellite Precipitation Products over Malaysia. Atmos. Res. 2018, 202, 63–76. [Google Scholar] [CrossRef]
- Li, G.; Yu, Z.; Wang, W.; Ju, Q.; Chen, X. Analysis of the Spatial Distribution of Precipitation and Topography with GPM Data in the Tibetan Plateau. Atmos. Res. 2021, 247, 105259. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 Legacy Products over Mainland China at Multiple Spatiotemporal Scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Zorzetto, E.; Marani, M. Downscaling of Rainfall Extremes from Satellite Observations. Water Resour. Res. 2019, 55, 156–174. [Google Scholar] [CrossRef]
- Moazami, S.; Najafi, M.R. A Comprehensive Evaluation of GPM-IMERG V06 and MRMS with Hourly Ground-Based Precipitation Observations across Canada. J. Hydrol. 2021, 594, 125929. [Google Scholar] [CrossRef]
- Khodadoust Siuki, S.; Saghafian, B.; Moazami, S. Comprehensive Evaluation of 3-Hourly TRMM and Half-Hourly GPM-IMERG Satellite Precipitation Products. Int. J. Remote Sens. 2017, 38, 558–571. [Google Scholar] [CrossRef]
- Rahmawati, N.; Lubczynski, M.W. Validation of Satellite Daily Rainfall Estimates in Complex Terrain of Bali Island, Indonesia. Theor. Appl. Climatol. 2018, 134, 513–532. [Google Scholar] [CrossRef]











| Name/Symbol | Formula | Optimal Value |
|---|---|---|
| Coefficient of determination/R2 | 1 | |
| Slope of linear regression/a | Y = aX + b | 1 |
| Root Mean Square Error/RMSE | 0 | |
| Mean Absolute Error/MAE | 0 | |
| Categorical statistical metrics | ||
| Probability of Detection/POD | 1 | |
| False Alarm Ratio/FAR | 0 | |
| Critical Success Index/CSI | 1 | |
| References/Study Area | Study Period/ Number of Rain Gauges for Validation | Validation Approach | CC or | RMSE mm/Day | MAE mm/Day | POD | FAR | CSI |
|---|---|---|---|---|---|---|---|---|
| [25]/East Africa | 2000–2018/36 | grid-to-grid | 0.41 | 12.4 | 7.6 | 0.88 | ||
| [66]/East Africa | 2014/37 | grid-to-grid | 0.53 | 0.87 | 0.04 | |||
| [68]/Singapore | 2014–2016/48 | grid-to-grid | 0.53 | 11.83 | 0.78 | 0.28 | 0.60 | |
| [63]/Philippines | 2014–2017/55 | grid-to-grid | 0.81 | 5.66 | 3.74 | |||
| [64]/Bali | 2015–2017/27 | point-to-grid | 0.32 | 17.19 | 0.84 | 0.54 | 0.44 | |
| [69]/Vietnam | 2014–2016 53 | grid-to-grid | 0.58 | 0.73 | 0.22 | 0.61 | ||
| [70]/Malaysia | 2014–2016/31 | point-to-grid | 0.54 | 14.93 | 0.89 | 0.20 | 0.73 | |
| [62]/Mexico | 2014–2015/99 | point-gridded | 0.54 | 7.93 | 0.2–0.6 | 0.2–0.6 | 0.2–0.8 | |
| Ankavia | 2018–2020/14 | point-gridded | 0.80 | 12 | 5.5 | 0.5–0.6 | 0.2–0.4 | 0.4–0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramahaimandimby, Z.; Randriamaherisoa, A.; Jonard, F.; Vanclooster, M.; Bielders, C.L. Reliability of Gridded Precipitation Products for Water Management Studies: The Case of the Ankavia River Basin in Madagascar. Remote Sens. 2022, 14, 3940. https://doi.org/10.3390/rs14163940
Ramahaimandimby Z, Randriamaherisoa A, Jonard F, Vanclooster M, Bielders CL. Reliability of Gridded Precipitation Products for Water Management Studies: The Case of the Ankavia River Basin in Madagascar. Remote Sensing. 2022; 14(16):3940. https://doi.org/10.3390/rs14163940
Chicago/Turabian StyleRamahaimandimby, Zonirina, Alain Randriamaherisoa, François Jonard, Marnik Vanclooster, and Charles L. Bielders. 2022. "Reliability of Gridded Precipitation Products for Water Management Studies: The Case of the Ankavia River Basin in Madagascar" Remote Sensing 14, no. 16: 3940. https://doi.org/10.3390/rs14163940
APA StyleRamahaimandimby, Z., Randriamaherisoa, A., Jonard, F., Vanclooster, M., & Bielders, C. L. (2022). Reliability of Gridded Precipitation Products for Water Management Studies: The Case of the Ankavia River Basin in Madagascar. Remote Sensing, 14(16), 3940. https://doi.org/10.3390/rs14163940