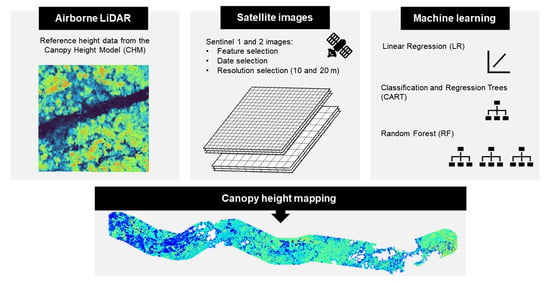
Canopy Height Mapping by Sentinel 1 and 2 Satellite Images, Airborne LiDAR Data, and Machine Learning
Abstract
:1. Introduction
- Evaluate the relationship between the vegetation height measured by LiDAR and S1 and S2 features, in two spatial resolutions (10 and 20 m) and different periods of the year.
- Define the best approach to modeling the vegetation height, in order to evaluate the best set of S1 and S2 features and their spatial resolution, the proper time of year, and the most suitable machine learning algorithms (LR, CART, or RF).
- To analyze the generalization ability of a model trained with orbital data from a given date to estimate height based on data from other periods of the year.
2. Materials and Methods
2.1. Study Area and Datasets
- sum = VV + VH
- ratio = VV/VH
- Normalized Difference Index or NDI = (VV − VH)/(VV + VH)
- Radar Vegetation Index or RVI = 4×VH/(VV+VH)
2.2. Vegetation Height Modeling and Mapping
3. Results
3.1. Relationship between LiDAR Height and Sentinel Features
3.2. Vegetation Height Estimation Based on Sentinel 1 SAR Data
3.3. Vegetation Height Estimation Based on Sentinel 2 Multispectral Data
3.4. Vegetation Height Estimation Based on the Integration of Sentinel 1 SAR Data and Sentinel 2 Multispectral Data
3.5. Generalization Ability of the Best Models
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abelleira Martínez, O.J.; Fremier, A.K.; Günter, S.; Ramos Bendaña, Z.; Vierling, L.; Galbraith, S.M.; Bosque-Pérez, N.A.; Ordoñez, J.C. Scaling up Functional Traits for Ecosystem Services with Remote Sensing: Concepts and Methods. Ecol. Evol. 2016, 6, 4359–4371. [Google Scholar] [CrossRef] [PubMed]
- Karna, Y.K.; Hussin, Y.A.; Gilani, H.; Bronsveld, M.C.; Murthy, M.S.R.; Qamer, F.M.; Karky, B.S.; Bhattarai, T.; Aigong, X.; Baniya, C.B. Integration of WorldView-2 and Airborne LiDAR Data for Tree Species Level Carbon Stock Mapping in Kayar Khola Watershed, Nepal. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 280–291. [Google Scholar] [CrossRef]
- Hyde, P.; Dubayah, R.; Walker, W.; Blair, J.B.; Hofton, M.; Hunsaker, C. Mapping Forest Structure for Wildlife Habitat Analysis Using Multi-Sensor (LiDAR, SAR/InSAR, ETM+, Quickbird) Synergy. Remote Sens. Environ. 2006, 102, 63–73. [Google Scholar] [CrossRef]
- Arroyo, L.A.; Pascual, C.; Manzanera, J.A. Fire Models and Methods to Map Fuel Types: The Role of Remote Sensing. For. Ecol. Manag. 2008, 256, 1239–1252. [Google Scholar] [CrossRef] [Green Version]
- Stojanova, D.; Panov, P.; Gjorgjioski, V.; Kobler, A.; Džeroski, S. Estimating Vegetation Height and Canopy Cover from Remotely Sensed Data with Machine Learning. Ecol. Inform. 2010, 5, 256–266. [Google Scholar] [CrossRef]
- Mills, S.J.; Gerardo Castro, M.P.; Li, Z.; Cai, J.; Hayward, R.; Mejias, L.; Walker, R.A. Evaluation of Aerial Remote Sensing Techniques for Vegetation Management in Power-Line Corridors. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3379–3390. [Google Scholar] [CrossRef]
- Wulder, M.A.; Seemann, D. Forest Inventory Height Update through the Integration of Lidar Data with Segmented Landsat Imagery. Can. J. Remote Sens. 2003, 29, 536–543. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Ongé, B.; Flood, M. LiDAR Remote Sensing of Forest Structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef] [Green Version]
- Trier, Ø.D.; Salberg, A.B.; Haarpaintner, J.; Aarsten, D.; Gobakken, T.; Næsset, E. Multi-Sensor Forest Vegetation Height Mapping Methods for Tanzania. Eur. J. Remote Sens. 2018, 51, 587–606. [Google Scholar] [CrossRef] [Green Version]
- Lang, N.; Schindler, K.; Wegner, J.D. Country-Wide High-Resolution Vegetation Height Mapping with Sentinel-2. Remote Sens. Environ. 2019, 233, 111347. [Google Scholar] [CrossRef] [Green Version]
- Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integration of Lidar and Landsat ETM+ Data for Estimating and Mapping Forest Canopy Height. Remote Sens. Environ. 2002, 82, 397–416. [Google Scholar] [CrossRef] [Green Version]
- Belgiu, M.; Dragut, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of Machine-Learning Classification in Remote Sensing: An Applied Review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.M.; Behera, M.D.; Paramanik, S. Canopy Height Estimation Using Sentinel Series Images through Machine Learning Models in a Mangrove Forest. Remote Sens. 2020, 12, 1519. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Goetz, S.J.; Turubanova, S.; Tyukavina, A.; Krylov, A.; Kommareddy, A.; Egorov, A. Mapping Tree Height Distributions in Sub-Saharan Africa Using Landsat 7 and 8 Data. Remote Sens. Environ. 2016, 185, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping Global Forest Canopy Height through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.; Saatchi, S.; Yu, Y.; Myneni, R.B. Estimation of Forest Aboveground Biomass in California Using Canopy Height and Leaf Area Index Estimated from Satellite Data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 Imagery for Forest Variable Prediction in Boreal Region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Korhonen, L.; Hadi; Packalen, P.; Rautiainen, M. Comparison of Sentinel-2 and Landsat 8 in the Estimation of Boreal Forest Canopy Cover and Leaf Area Index. Remote Sens. Environ. 2017, 195, 259–274. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Siachalou, S.; Patias, P. Assessing the Relationships between Growing Stock Volume and Sentinel-2 Imagery in a Mediterranean Forest Ecosystem. Remote Sens. Lett. 2017, 8, 508–517. [Google Scholar] [CrossRef]
- Luckman, A.; Baker, J.; Kuplich, T.M.; Corina da Costa, F.Y.; Alejandro, C.F. A Study of the Relationship between Radar Backscatter and Regenerating Tropical Forest Biomass for Spaceborne SAR Instruments. Remote Sens. Environ. 1997, 60, 1–13. [Google Scholar] [CrossRef]
- Bispo, P.d.C.; Rodríguez-Veiga, P.; Zimbres, B.; do Couto de Miranda, S.; Giusti Cezare, C.H.; Fleming, S.; Baldacchino, F.; Louis, V.; Rains, D.; Garcia, M.; et al. Woody Aboveground Biomass Mapping of the Brazilian Savanna with a Multi-Sensor and Machine Learning Approach. Remote Sens. 2020, 12, 2685. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Cuozzo, G.; Padovano, A.; Notarnicola, C.; Albinet, C. Machine-Learning Applications for the Retrieval of Forest Biomass from Airborne P-Band SAR Data. Remote Sens. 2020, 12, 804. [Google Scholar] [CrossRef] [Green Version]
- Soja, M.J.; Quegan, S.; d’Alessandro, M.M.; Banda, F.; Scipal, K.; Tebaldini, S.; Ulander, L.M.H. Mapping Above-Ground Biomass in Tropical Forests with Ground-Cancelled P-Band SAR and Limited Reference Data. Remote Sens. Environ. 2021, 253, 112153. [Google Scholar] [CrossRef]
- Schlund, M.; Davidson, M.W.J. Aboveground Forest Biomass Estimation Combining L- and P-Band SAR Acquisitions. Remote Sens. 2018, 10, 1151. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Gong, W.; Xing, Y.; Hu, X.; Gong, J. Estimation of the Forest Stand Mean Height and Aboveground Biomass in Northeast China Using SAR Sentinel-1B, Multispectral Sentinel-2A, and DEM Imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 277–289. [Google Scholar] [CrossRef]
- Moghaddam, M.; Dungan, J.L.; Acker, S. Forest Variable Estimation from Fusion of SAR and Multispectral Optical Data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2176–2187. [Google Scholar] [CrossRef]
- Morin, D.; Planells, M.; Baghdadi, N.; Bouvet, A.; Fayad, I.; Le Toan, T.; Mermoz, S.; Villard, L. Improving Heterogeneous Forest Height Maps by Integrating GEDI-Based Forest Height Information in a Multi-Sensor Mapping Process. Remote Sens. 2022, 14, 2079. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-Resolution Mapping of Forest Canopy Height Using Machine Learning by Coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 Data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Nasirzadehdizaji, R.; Sanli, F.B.; Abdikan, S.; Cakir, Z.; Sekertekin, A.; Ustuner, M. Sensitivity Analysis of Multi-Temporal Sentinel-1 SAR Parameters to Crop Height and Canopy Coverage. Appl. Sci. 2019, 9, 655. [Google Scholar] [CrossRef] [Green Version]
- Osborne, J.; Waters, E. Four Assumptions of Multiple Regression That Researchers Should Always Test. Pract. Assess. Res. Eval. 2002, 8, 1. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Pourshamsi, M.; Xia, J.; Yokoya, N.; Garcia, M.; Lavalle, M.; Pottier, E.; Balzter, H. Tropical Forest Canopy Height Estimation from Combined Polarimetric SAR and LiDAR Using Machine-Learning. ISPRS J. Photogramm. Remote Sens. 2021, 172, 79–94. [Google Scholar] [CrossRef]
- Kugler, F.; Lee, S.K.; Hajnsek, I.; Papathanassiou, K.P. Forest Height Estimation by Means of Pol-InSAR Data Inversion: The Role of the Vertical Wavenumber. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5294–5311. [Google Scholar] [CrossRef]
- Fatoyinbo, T.; Armston, J.; Simard, M.; Saatchi, S.; Denbina, M.; Lavalle, M.; Hofton, M.; Tang, H.; Marselis, S.; Pinto, N.; et al. The NASA AfriSAR Campaign: Airborne SAR and Lidar Measurements of Tropical Forest Structure and Biomass in Support of Current and Future Space Missions. Remote Sens. Environ. 2021, 264, 112533. [Google Scholar] [CrossRef]
- Banda, F.; Giudici, D.; Le Toan, T.; d’Alessandro, M.M.; Papathanassiou, K.; Quegan, S.; Riembauer, G.; Scipal, K.; Soja, M.; Tebaldini, S.; et al. The BIOMASS Level 2 Prototype Processor: Design and Experimental Results of above-Ground Biomass Estimation. Remote Sens. 2020, 12, 985. [Google Scholar] [CrossRef] [Green Version]
- Wood, E.M.; Pidgeon, A.M.; Radeloff, V.C.; Keuler, N.S. Image Texture as a Remotely Sensed Measure of Vegetation Structure. Remote Sens. Environ. 2012, 121, 516–526. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Inkinen, M.; Engdahl, M.; Linko, S.; Zhu, Y.H. Accuracy Comparison of Various Remote Sensing Data Sources in the Retrieval of Forest Stand Attributes. For. Ecol. Manag. 2000, 128, 109–120. [Google Scholar] [CrossRef]











| S2 Band | Description | Central Wavelength | Resolution |
|---|---|---|---|
| B02 | Blue | 490 nm | 10 m (original) and 20 m (resampled) |
| B03 | Green | 560 nm | 10 m (original) and 20 m (resampled) |
| B04 | Red | 665 nm | 10 m (original) and 20 m (resampled) |
| B05 | Red Edge 1 | 705 nm | 20 m (original) |
| B06 | Red Edge 2 | 740 nm | 20 m (original) |
| B07 | Red Edge 3 | 783 nm | 20 m (original) |
| B08 | NIR 1 | 842 nm | 10 m (original) and 20 m (resampled) |
| B8A | NIR 2 | 865 nm | 20 m (original) |
| B11 | SWIR 1 | 1610 nm | 20 m (original) |
| B12 | SWIR 2 | 2190 nm | 20 m (original) |
| Vegetation Index | Formula | Resolution |
|---|---|---|
| Simple Ratio (SR) | SR = B08/B04 | 10 and 20 m |
| Normalized Difference Vegetation Index (NDVI) | NDVI = (B08 − B04)/(B08 + B04) | 10 and 20 m |
| Green Normalized Difference Vegetation Index (GNDVI) | GNDVI = (B08 − B03)/(B08 + B03) | 10 and 20 m |
| Vegetation Index green (VIgreen) | VIgreen = (B03 − B04)/(B03 + B04) | 10 and 20 m |
| Red Edge Normalized Difference Vegetation Index (RENDVI) | RENDVI = (B07 − B04)/(B07 + B04) | 20 m |
| Red Edge Simple Ratio (SRRE) | SRRE = B05/B04 | 20 m |
| Red edge Ratio Index 1 (RRI1) | RRI1 = B8A/B05 | 20 m |
| Inverted Red Edge Chlorophyll Index (IRECI) | IRECI = (B07−B04)/(B05/B06) | 20 m |
| Moisture Stress Index (MSI) | MSI = B11/B8A | 20 m |
| Normalized Difference Infrared Index (NDII) | NDII = (B8A − B11)/(B8A + B11) | 20 m |
| Normalized Burn Ratio (NBR) | NBR = (B8A − B12)/(B8A + B12) | 20 m |
| Specific Leaf Area Vegetation Index (SLAVI) | SLAVI = B8A/(B05 + B12) | 20 m |
| Algorithm | Features (*) | Resolution | Date | MAE | RMSE | R2 |
|---|---|---|---|---|---|---|
| LR | raw (2) | 10 m | May 22 | 6.13 | 7.65 | 0.16 |
| ind (2) | 10 m | May 22 | 6.10 | 7.62 | 0.16 | |
| all (3) | 10 m | May 22 | 6.19 | 7.69 | 0.15 | |
| raw (2) | 10 m | Sep 07 | 5.77 | 7.16 | 0.28 | |
| ind (2) | 10 m | Sep 07 | 5.73 | 7.13 | 0.29 | |
| all (3) | 10 m | Sep 07 | 5.76 | 7.15 | 0.29 | |
| raw (2) | 10 m | Oct 25 | 5.95 | 7.38 | 0.20 | |
| ind (2) | 10 m | Oct 25 | 6.00 | 7.40 | 0.20 | |
| all (3) | 10 m | Oct 25 | 5.97 | 7.39 | 0.20 | |
| raw (2) | 20 m | May 22 | 5.33 | 6.55 | 0.12 | |
| ind (2) | 20 m | May 22 | 5.31 | 6.54 | 0.12 | |
| all (3) | 20 m | May 22 | 5.37 | 6.61 | 0.10 | |
| raw (2) | 20 m | Sep 07 | 5.12 | 6.30 | 0.20 | |
| ind (2) | 20 m | Sep 07 | 5.08 | 6.27 | 0.20 | |
| all (3) | 20 m | Sep 07 | 4.97 | 6.19 | 0.24 | |
| raw (2) | 20 m | Oct 25 | 5.14 | 6.32 | 0.20 | |
| ind (2) | 20 m | Oct 25 | 5.19 | 6.33 | 0.19 | |
| all (3) | 20 m | Oct 25 | 5.10 | 6.42 | 0.15 | |
| CART | raw | 10 m | May 22 | 6.80 | 8.37 | 0.23 |
| ind | 10 m | May 22 | 6.35 | 7.81 | 0.17 | |
| all | 10 m | May 22 | 7.36 | 9.07 | 0.21 | |
| raw (2) | 10 m | Sep 07 | 5.52 | 7.10 | 0.30 | |
| ind (2) | 10 m | Sep 07 | 5.69 | 7.36 | 0.34 | |
| all (3) | 10 m | Sep 07 | 5.64 | 7.11 | 0.32 | |
| raw (2) | 10 m | Oct 25 | 6.70 | 8.52 | 0.12 | |
| ind (2) | 10 m | Oct 25 | 6.55 | 8.39 | 0.18 | |
| all (3) | 10 m | Oct 25 | 6.57 | 8.54 | 0.11 | |
| raw (2) | 20 m | May 22 | 5.99 | 7.61 | 0.06 | |
| ind (2) | 20 m | May 22 | 6.05 | 7.37 | 0.06 | |
| all (3) | 20 m | May 22 | 6.13 | 7.70 | 0.05 | |
| raw (2) | 20 m | Sep 07 | 5.24 | 6.64 | 0.30 | |
| ind (2) | 20 m | Sep 07 | 5.17 | 6.59 | 0.26 | |
| all (3) | 20 m | Sep 07 | 5.27 | 6.65 | 0.30 | |
| raw (2) | 20 m | Oct 25 | 5.40 | 6.95 | 0.14 | |
| ind (2) | 20 m | Oct 25 | 5.73 | 7.29 | 0.15 | |
| all (3) | 20 m | Oct 25 | 5.79 | 7.29 | 0.13 | |
| RF | raw | 10 m | May 22 | 6.52 | 8.17 | 0.17 |
| ind | 10 m | May 22 | 6.39 | 7.74 | 0.16 | |
| all | 10 m | May 22 | 6.58 | 8.06 | 0.13 | |
| raw (2) | 10 m | Sep 07 | 5.81 | 7.44 | 0.25 | |
| ind (2) | 10 m | Sep 07 | 5.93 | 7.47 | 0.30 | |
| all (3) | 10 m | Sep 07 | 5.84 | 7.44 | 0.27 | |
| raw (2) | 10 m | Oct 25 | 6.52 | 8.16 | 0.13 | |
| ind (2) | 10 m | Oct 25 | 6.33 | 8.26 | 0.11 | |
| all (3) | 10 m | Oct 25 | 6.29 | 8.05 | 0.14 | |
| raw (2) | 20 m | May 22 | 6.21 | 7.58 | 0.04 | |
| ind (2) | 20 m | May 22 | 5.84 | 7.27 | 0.04 | |
| all (3) | 20 m | May 22 | 6.01 | 7.36 | 0.02 | |
| raw (2) | 20 m | Sep 07 | 5.27 | 6.79 | 0.27 | |
| ind (2) | 20 m | Sep 07 | 5.18 | 6.66 | 0.23 | |
| all (3) | 20 m | Sep 07 | 5.22 | 6.73 | 0.27 | |
| raw (2) | 20 m | Oct 25 | 5.44 | 6.70 | 0.15 | |
| ind (2) | 20 m | Oct 25 | 5.46 | 6.85 | 0.16 | |
| all (3) | 20 m | Oct 25 | 5.42 | 6.80 | 0.15 |
| Algorithm | Features (*) | Resolution | Date | MAE | RMSE | R2 |
|---|---|---|---|---|---|---|
| LR | raw (4) | 10 m | May 19 | 6.73 | 8.24 | 0.15 |
| ind (3) | 10 m | May 19 | 7.40 | 10.37 | 0.14 | |
| all (7) | 10 m | May 19 | 6.81 | 8.81 | 0.20 | |
| raw (4) | 10 m | Oct 26 | 5.55 | 7.08 | 0.36 | |
| ind (3) | 10 m | Oct 26 | 5.95 | 7.37 | 0.35 | |
| all (7) | 10 m | Oct 26 | 5.43 | 6.68 | 0.38 | |
| raw (4) | 10 m | Nov 30 | 5.46 | 6.71 | 0.33 | |
| ind (3) | 10 m | Nov 30 | 5.60 | 6.86 | 0.29 | |
| all (7) | 10 m | Nov 30 | 5.68 | 7.31 | 0.34 | |
| raw (6) | 20 m | May 19 | 5.02 | 6.31 | 0.26 | |
| ind (8) | 20 m | May 19 | 5.90 | 8.84 | 0.27 | |
| all (14) | 20 m | May 19 | 5.35 | 7.08 | 0.31 | |
| raw (6) | 20 m | Oct 26 | 4.35 | 5.61 | 0.45 | |
| ind (8) | 20 m | Oct 26 | 4.62 | 6.18 | 0.43 | |
| all (14) | 20 m | Oct 26 | 4.02 | 5.15 | 0.56 | |
| raw (6) | 20 m | Nov 30 | 4.50 | 5.85 | 0.37 | |
| ind (8) | 20 m | Nov 30 | 4.57 | 6.09 | 0.47 | |
| all (14) | 20 m | Nov 30 | 3.92 | 4.91 | 0.54 | |
| CART | raw (4) | 10 m | May 19 | 7.52 | 8.79 | 0.08 |
| ind (3) | 10 m | May 19 | 6.82 | 8.33 | 0.13 | |
| all (7) | 10 m | May 19 | 7.34 | 8.94 | 0.09 | |
| raw (4) | 10 m | Oct 26 | 6.59 | 7.94 | 0.17 | |
| ind (3) | 10 m | Oct 26 | 5.62 | 7.17 | 0.31 | |
| all (7) | 10 m | Oct 26 | 5.93 | 7.60 | 0.25 | |
| raw (4) | 10 m | Nov 30 | 6.04 | 7.28 | 0.29 | |
| ind (3) | 10 m | Nov 30 | 6.04 | 7.45 | 0.28 | |
| all (7) | 10 m | Nov 30 | 6.17 | 7.79 | 0.25 | |
| raw (6) | 20 m | May 19 | 5.73 | 7.03 | 0.23 | |
| ind (8) | 20 m | May 19 | 5.83 | 7.07 | 0.15 | |
| all (14) | 20 m | May 19 | 5.67 | 6.97 | 0.16 | |
| raw (6) | 20 m | Oct 26 | 4.56 | 5.78 | 0.43 | |
| ind (8) | 20 m | Oct 26 | 4.93 | 6.34 | 0.36 | |
| all (14) | 20 m | Oct 26 | 5.01 | 6.22 | 0.38 | |
| raw (6) | 20 m | Nov 30 | 4.41 | 5.38 | 0.46 | |
| ind (8) | 20 m | Nov 30 | 4.68 | 5.60 | 0.38 | |
| all (14) | 20 m | Nov 30 | 4.82 | 5.60 | 0.40 | |
| RF | raw (4) | 10 m | May 19 | 6.91 | 8.31 | 0.14 |
| ind (3) | 10 m | May 19 | 6.78 | 8.19 | 0.14 | |
| all (7) | 10 m | May 19 | 6.69 | 8.05 | 0.17 | |
| raw (4) | 10 m | Oct 26 | 6.07 | 7.44 | 0.24 | |
| ind (3) | 10 m | Oct 26 | 6.00 | 7.32 | 0.25 | |
| all (7) | 10 m | Oct 26 | 5.71 | 6.98 | 0.33 | |
| raw (4) | 10 m | Nov 30 | 5.87 | 6.92 | 0.33 | |
| ind (3) | 10 m | Nov 30 | 6.16 | 7.62 | 0.22 | |
| all (7) | 10 m | Nov 30 | 5.64 | 6.76 | 0.35 | |
| raw (6) | 20 m | May 19 | 5.17 | 6.31 | 0.23 | |
| ind (8) | 20 m | May 19 | 4.95 | 6.06 | 0.28 | |
| all (14) | 20 m | May 19 | 4.98 | 6.08 | 0.25 | |
| raw (6) | 20 m | Oct 26 | 3.88 | 4.92 | 0.58 | |
| ind (8) | 20 m | Oct 26 | 4.05 | 5.06 | 0.50 | |
| all (14) | 20 m | Oct 26 | 3.95 | 4.90 | 0.55 | |
| raw (6) | 20 m | Nov 30 | 3.92 | 4.79 | 0.55 | |
| ind (8) | 20 m | Nov 30 | 4.00 | 4.94 | 0.51 | |
| all (14) | 20 m | Nov 30 | 3.97 | 4.84 | 0.53 |
| Algorithm | Features (*) | Resolution | Date | MAE | RMSE | R2 |
|---|---|---|---|---|---|---|
| LR | raw (6) | 10 m | May 22 (S1) and 19 (S2) | 6.55 | 8.15 | 0.17 |
| ind (5) | 10 m | May 22 (S1) and 19 (S2) | 7.22 | 10.24 | 0.15 | |
| all (10) | 10 m | May 22 (S1) and 19 (S2) | 6.91 | 9.31 | 0.17 | |
| raw (6) | 10 m | Oct 25 (S1) and 26 (S2) | 5.36 | 7.03 | 0.42 | |
| ind (5) | 10 m | Oct 25 (S1) and 26 (S2) | 5.36 | 6.76 | 0.38 | |
| all (10) | 10 m | Oct 25 (S1) and 26 (S2) | 5.03 | 6.17 | 0.45 | |
| raw (8) | 20 m | May 22 (S1) and 19 (S2) | 5.15 | 6.49 | 0.25 | |
| ind (10) | 20 m | May 22 (S1) and 19 (S2) | 5.78 | 8.56 | 0.24 | |
| all (17) | 20 m | May 22 (S1) and 19 (S2) | 5.47 | 7.27 | 0.26 | |
| raw (8) | 20 m | Oct 25 (S1) and 26 (S2) | 4.34 | 5.54 | 0.50 | |
| ind (10) | 20 m | Oct 25 (S1) and 26 (S2) | 4.22 | 5.76 | 0.48 | |
| all (17) | 20 m | Oct 25 (S1) and 26 (S2) | 4.19 | 5.29 | 0.56 | |
| CART | raw (6) | 10 m | May 22 (S1) and 19 (S2) | 7.33 | 8.84 | 0.12 |
| ind (5) | 10 m | May 22 (S1) and 19 (S2) | 6.37 | 7.76 | 0.20 | |
| all (10) | 10 m | May 22 (S1) and 19 (S2) | 7.38 | 9.13 | 0.14 | |
| raw (6) | 10 m | Oct 25 (S1) and 26 (S2) | 6.44 | 7.85 | 0.25 | |
| ind (5) | 10 m | Oct 25 (S1) and 26 (S2) | 5.73 | 7.35 | 0.29 | |
| all (10) | 10 m | Oct 25 (S1) and 26 (S2) | 5.73 | 7.37 | 0.33 | |
| raw (8) | 20 m | May 22 (S1) and 19 (S2) | 5.38 | 6.70 | 0.21 | |
| ind (10) | 20 m | May 22 (S1) and 19 (S2) | 5.55 | 6.74 | 0.17 | |
| all (17) | 20 m | May 22 (S1) and 19 (S2) | 5.25 | 6.58 | 0.22 | |
| raw (8) | 20 m | Oct 25 (S1) and 26 (S2) | 4.20 | 5.28 | 0.50 | |
| ind (10) | 20 m | Oct 25 (S1) and 26 (S2) | 4.89 | 6.22 | 0.38 | |
| all (17) | 20 m | Oct 25 (S1) and 26 (S2) | 5.06 | 6.25 | 0.37 | |
| RF | raw (6) | 10 m | May 22 (S1) and 19 (S2) | 6.37 | 7.78 | 0.13 |
| ind (5) | 10 m | May 22 (S1) and 19 (S2) | 6.20 | 7.55 | 0.16 | |
| all (10) | 10 m | May 22 (S1) and 19 (S2) | 6.35 | 7.71 | 0.15 | |
| raw (6) | 10 m | Oct 25 (S1) and 26 (S2) | 5.80 | 7.22 | 0.28 | |
| ind (5) | 10 m | Oct 25 (S1) and 26 (S2) | 5.09 | 6.38 | 0.45 | |
| all (10) | 10 m | Oct 25 (S1) and 26 (S2) | 5.19 | 6.52 | 0.40 | |
| raw (8) | 20 m | May 22 (S1) and 19 (S2) | 5.02 | 6.15 | 0.21 | |
| ind (10) | 20 m | May 22 (S1) and 19 (S2) | 4.83 | 5.94 | 0.31 | |
| all (17) | 20 m | May 22 (S1) and 19 (S2) | 4.90 | 5.97 | 0.24 | |
| raw (8) | 20 m | Oct 25 (S1) and 26 (S2) | 3.62 | 4.86 | 0.60 | |
| ind (10) | 20 m | Oct 25 (S1) and 26 (S2) | 3.77 | 4.83 | 0.56 | |
| all (17) | 20 m | Oct 25 (S1) and 26 (S2) | 3.67 | 4.71 | 0.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres de Almeida, C.; Gerente, J.; Rodrigo dos Prazeres Campos, J.; Caruso Gomes Junior, F.; Providelo, L.A.; Marchiori, G.; Chen, X. Canopy Height Mapping by Sentinel 1 and 2 Satellite Images, Airborne LiDAR Data, and Machine Learning. Remote Sens. 2022, 14, 4112. https://doi.org/10.3390/rs14164112
Torres de Almeida C, Gerente J, Rodrigo dos Prazeres Campos J, Caruso Gomes Junior F, Providelo LA, Marchiori G, Chen X. Canopy Height Mapping by Sentinel 1 and 2 Satellite Images, Airborne LiDAR Data, and Machine Learning. Remote Sensing. 2022; 14(16):4112. https://doi.org/10.3390/rs14164112
Chicago/Turabian StyleTorres de Almeida, Catherine, Jéssica Gerente, Jamerson Rodrigo dos Prazeres Campos, Francisco Caruso Gomes Junior, Lucas Antonio Providelo, Guilherme Marchiori, and Xinjian Chen. 2022. "Canopy Height Mapping by Sentinel 1 and 2 Satellite Images, Airborne LiDAR Data, and Machine Learning" Remote Sensing 14, no. 16: 4112. https://doi.org/10.3390/rs14164112
APA StyleTorres de Almeida, C., Gerente, J., Rodrigo dos Prazeres Campos, J., Caruso Gomes Junior, F., Providelo, L. A., Marchiori, G., & Chen, X. (2022). Canopy Height Mapping by Sentinel 1 and 2 Satellite Images, Airborne LiDAR Data, and Machine Learning. Remote Sensing, 14(16), 4112. https://doi.org/10.3390/rs14164112