Figure 1.
(
A) Phoenix Lidar Systems
® Scout-32, featuring a Velodyne
® HDL–32E Lidar Scanner and Sony
® Alpha A6000 24 MP camera, with a (
B) diagram of Velodyne
® HDL–32E, highlighting (a) 32 individual, vertically stacked scanner/receiver pairs that rotate about (b) a central axis oriented through (c) a focal point as they scan a target area. Adapted from [
13].
Figure 1.
(
A) Phoenix Lidar Systems
® Scout-32, featuring a Velodyne
® HDL–32E Lidar Scanner and Sony
® Alpha A6000 24 MP camera, with a (
B) diagram of Velodyne
® HDL–32E, highlighting (a) 32 individual, vertically stacked scanner/receiver pairs that rotate about (b) a central axis oriented through (c) a focal point as they scan a target area. Adapted from [
13].
Figure 2.
Livox® Mid–40 as mounted on a camera tripod.
Figure 2.
Livox® Mid–40 as mounted on a camera tripod.
Figure 3.
Rosette-style scan pattern of the Livox® Mid–40, over a course of three seconds of operation. From left to right, each circle depicts the addition of one-second’s worth of data from a stationary scanner observing a stationary target surface.
Figure 3.
Rosette-style scan pattern of the Livox® Mid–40, over a course of three seconds of operation. From left to right, each circle depicts the addition of one-second’s worth of data from a stationary scanner observing a stationary target surface.
Figure 4.
Orientation of (A) the Velodyne® HDL–32E and (B) Livox® Mid–40 during indoor data collection. The scanner orientations shown here were used for all data collection (indoor and outdoor) throughout the duration of this study.
Figure 4.
Orientation of (A) the Velodyne® HDL–32E and (B) Livox® Mid–40 during indoor data collection. The scanner orientations shown here were used for all data collection (indoor and outdoor) throughout the duration of this study.
Figure 5.
Velodyne® HDL–32E raw observations as points representing scan lines from all 32 individual channels (even numbers 0 through 30 from left to right, followed by odd numbers 1 through 31 from left to right).
Figure 5.
Velodyne® HDL–32E raw observations as points representing scan lines from all 32 individual channels (even numbers 0 through 30 from left to right, followed by odd numbers 1 through 31 from left to right).
Figure 6.
Velodyne® HDL – 32E measurement analysis workflow.
Figure 6.
Velodyne® HDL – 32E measurement analysis workflow.
Figure 7.
Breakdown of example Mid–40 data from (A) raw observations, colorized by measured distance, to (B) a 100 × 100 array of cells colorized by range of average distance measurements per cell.
Figure 7.
Breakdown of example Mid–40 data from (A) raw observations, colorized by measured distance, to (B) a 100 × 100 array of cells colorized by range of average distance measurements per cell.
Figure 8.
Study site and target surface at the University of Florida. Top: The scanners were oriented at the side of an adjacent parking garage (yellow) at standoff distances to reflect a sUAS topographic data collection. Bottom: Scanner observations relative to each scanner are shown with extracted subsections highlighted in red. In order to facilitate reporting of results, the subsections of the target surface are designated W1 through W4, with W1 being the lowest and W4 being the highest observed by the scanners.
Figure 8.
Study site and target surface at the University of Florida. Top: The scanners were oriented at the side of an adjacent parking garage (yellow) at standoff distances to reflect a sUAS topographic data collection. Bottom: Scanner observations relative to each scanner are shown with extracted subsections highlighted in red. In order to facilitate reporting of results, the subsections of the target surface are designated W1 through W4, with W1 being the lowest and W4 being the highest observed by the scanners.
Figure 9.
(A) Alignment targets used for absolute accuracy assessment and their locations as observed with the (B) Livox® Mid–40 and (C) Velodyne® HDL–32E are shown in selections from each scanner’s point clouds.
Figure 9.
(A) Alignment targets used for absolute accuracy assessment and their locations as observed with the (B) Livox® Mid–40 and (C) Velodyne® HDL–32E are shown in selections from each scanner’s point clouds.
Figure 10.
Point clouds generated by the Riegl® VZ-400, representing the (A) Livox® Mid–40 and the (B) Velodyne® HDL–32E.
Figure 10.
Point clouds generated by the Riegl® VZ-400, representing the (A) Livox® Mid–40 and the (B) Velodyne® HDL–32E.
Figure 11.
Velodyne® HDL–32E with individual scanner and receiver pairs (32 total) plotted along central axis with focal point locations plotted for every 0.01° of rotation (A) with and (B) without the scanner point cloud.
Figure 11.
Velodyne® HDL–32E with individual scanner and receiver pairs (32 total) plotted along central axis with focal point locations plotted for every 0.01° of rotation (A) with and (B) without the scanner point cloud.
Figure 12.
Projection of Velodyne® HDL–32E scan lines in (A) the Riegl® VZ-400 point clouds and (B) their interpolation as an additional scalar field on the target surface.
Figure 12.
Projection of Velodyne® HDL–32E scan lines in (A) the Riegl® VZ-400 point clouds and (B) their interpolation as an additional scalar field on the target surface.
Figure 13.
Alignment of (A) the Livox® Mid–40-point cloud with (B) the Riegl® VZ-400 point cloud using alignment targets placed on the target surface and (C) subsequent interpolation of scalar fields.
Figure 13.
Alignment of (A) the Livox® Mid–40-point cloud with (B) the Riegl® VZ-400 point cloud using alignment targets placed on the target surface and (C) subsequent interpolation of scalar fields.
Figure 14.
Velodyne® HDL–32E average distance measurements over time (average of all points from all 32 scanners within the −8° to +8° scan window) with variations in scanner precision highlighted.
Figure 14.
Velodyne® HDL–32E average distance measurements over time (average of all points from all 32 scanners within the −8° to +8° scan window) with variations in scanner precision highlighted.
Figure 15.
Comparison of individual channels’ average measured distances for the Velodyne® HDL–32E. The two pairs shown are the ones with the highest (channel 20) and lowest (channel 7) precision in their averaged measurements over time.
Figure 15.
Comparison of individual channels’ average measured distances for the Velodyne® HDL–32E. The two pairs shown are the ones with the highest (channel 20) and lowest (channel 7) precision in their averaged measurements over time.
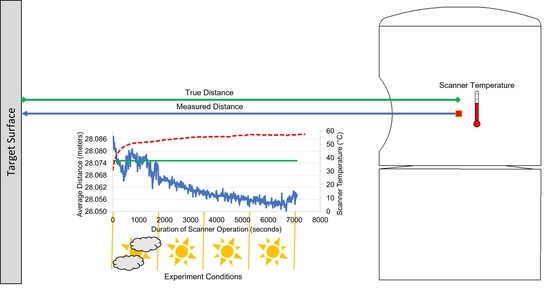
Figure 16.
Velodyne® HDL–32E indoor experiment overall average measured distances (m) plotted over time elapsed with scanner internal temperature (°C).
Figure 16.
Velodyne® HDL–32E indoor experiment overall average measured distances (m) plotted over time elapsed with scanner internal temperature (°C).
Figure 17.
Linear relationship and correlation between Velodyne® HDL–32E internal temperature and overall average measured distance through the duration of indoor experiments. Equation for linear line of best fit and corresponding R2 values are shown on the figure.
Figure 17.
Linear relationship and correlation between Velodyne® HDL–32E internal temperature and overall average measured distance through the duration of indoor experiments. Equation for linear line of best fit and corresponding R2 values are shown on the figure.
Figure 18.
R2 values for the linear trendlines and internal temperature/average measured distance for each of the Velodyne® HDL – 32E’s individual channels.
Figure 18.
R2 values for the linear trendlines and internal temperature/average measured distance for each of the Velodyne® HDL – 32E’s individual channels.
Figure 19.
Linear relationship and correlation between Velodyne® HDL – 32E internal temperature and average measured distances for the individual channels with the highest (channel 14) and lowest (channel 29) R2 through the duration of indoor experiments. Equation for linear line of best fit and corresponding R2 values are shown on the figure.
Figure 19.
Linear relationship and correlation between Velodyne® HDL – 32E internal temperature and average measured distances for the individual channels with the highest (channel 14) and lowest (channel 29) R2 through the duration of indoor experiments. Equation for linear line of best fit and corresponding R2 values are shown on the figure.
Figure 20.
Average measured distance of all 32 individual channels versus internal scanner temperature and “true” distance value for both (A) night and (B) day iterations of the Velodyne® HDL–32E absolute accuracy experiment.
Figure 20.
Average measured distance of all 32 individual channels versus internal scanner temperature and “true” distance value for both (A) night and (B) day iterations of the Velodyne® HDL–32E absolute accuracy experiment.
Figure 21.
Calculated error (m) per individual channel, per subsections of target surface in Velodyne® HDL–32E during a 30 m (A) night experiment and a (B) day experiment. The green box highlights the reduced error observed when individual channels with offset angles greater than 15° are removed from the results, with the red box encompassing the total observed error by all individual scanners.
Figure 21.
Calculated error (m) per individual channel, per subsections of target surface in Velodyne® HDL–32E during a 30 m (A) night experiment and a (B) day experiment. The green box highlights the reduced error observed when individual channels with offset angles greater than 15° are removed from the results, with the red box encompassing the total observed error by all individual scanners.
Figure 22.
RMSE (m) per Velodyne® HDL–32E observation file for both (A) night and (B) day iterations of absolute accuracy experiments.
Figure 22.
RMSE (m) per Velodyne® HDL–32E observation file for both (A) night and (B) day iterations of absolute accuracy experiments.
Figure 23.
Weather conditions during Velodyne® HDL–32E night and day absolute accuracy experiments: (A) air temperature (°C), (B) barometric pressure (inches of mercury), and (C) solar radiation (watts per square meter) at study site. (D) Comparison between solar radiation and measured distance.
Figure 23.
Weather conditions during Velodyne® HDL–32E night and day absolute accuracy experiments: (A) air temperature (°C), (B) barometric pressure (inches of mercury), and (C) solar radiation (watts per square meter) at study site. (D) Comparison between solar radiation and measured distance.
Figure 24.
Linear relationship between Velodyne® HDL–32E average distance measurements and internal temperature for both night and day experiments, (A) with and (B) without the interference caused by solar radiation, with average truth values plotted for each experiment.
Figure 24.
Linear relationship between Velodyne® HDL–32E average distance measurements and internal temperature for both night and day experiments, (A) with and (B) without the interference caused by solar radiation, with average truth values plotted for each experiment.
Figure 25.
Average measured distance of the Livox® Mid–40’s field of view over time during indoor experiments.
Figure 25.
Average measured distance of the Livox® Mid–40’s field of view over time during indoor experiments.
Figure 26.
Raster of Livox® Mid–40 field of view, colorized by range of distance measurements per cell over duration of three-hour indoor experiments.
Figure 26.
Raster of Livox® Mid–40 field of view, colorized by range of distance measurements per cell over duration of three-hour indoor experiments.
Figure 27.
Livox® Mid–40 indoor point cloud (subset of 10 observation files), colorized by surface point density (points per cm).
Figure 27.
Livox® Mid–40 indoor point cloud (subset of 10 observation files), colorized by surface point density (points per cm).
Figure 28.
Raw observations of the Livox® Mid–40 during outdoor experiments, colored by measured distance from scanner origin.
Figure 28.
Raw observations of the Livox® Mid–40 during outdoor experiments, colored by measured distance from scanner origin.
Figure 29.
(A) Average measured distance and (B) running average measured distance per 60 s of the Livox® Mid–40’s field of view over time during outdoor accuracy assessments.
Figure 29.
(A) Average measured distance and (B) running average measured distance per 60 s of the Livox® Mid–40’s field of view over time during outdoor accuracy assessments.
Figure 30.
Range of measurements for the Livox® Mid–40 during (A) night and (B) day experiments, (C) colored by percentile.
Figure 30.
Range of measurements for the Livox® Mid–40 during (A) night and (B) day experiments, (C) colored by percentile.
Figure 31.
(
A) Livox
® Mid–40 and (
B) Riegl
® VZ-400 point clouds generated from observations of the target surface. CloudCompare [
21] was used to register the two datasets using the targets towards extraction of conjugate points for measured distance comparison (RMSE of 0.007 m, and 0.005 m for night and day target registrations, respectively).
Figure 31.
(
A) Livox
® Mid–40 and (
B) Riegl
® VZ-400 point clouds generated from observations of the target surface. CloudCompare [
21] was used to register the two datasets using the targets towards extraction of conjugate points for measured distance comparison (RMSE of 0.007 m, and 0.005 m for night and day target registrations, respectively).
Figure 32.
Livox® Mid–40 distribution of error in (A) night and (B) day experiments, (C) colored by percentile.
Figure 32.
Livox® Mid–40 distribution of error in (A) night and (B) day experiments, (C) colored by percentile.
Figure 33.
Livox® Mid–40 distance measurements (running average, per 60 s) and ongoing weather conditions (A) air temperature, (B) barometric pressure, and (C) solar radiation during day experiment.
Figure 33.
Livox® Mid–40 distance measurements (running average, per 60 s) and ongoing weather conditions (A) air temperature, (B) barometric pressure, and (C) solar radiation during day experiment.
Figure 34.
Temporal Stability of Velodyne® HDL–32E and Livox® Mid–40 during indoor experiments.
Figure 34.
Temporal Stability of Velodyne® HDL–32E and Livox® Mid–40 during indoor experiments.
Figure 35.
Calculated (A) standard deviation and (B) range of Velodyne® HDL–32E and Livox® Mid–40 over duration for all experiments.
Figure 35.
Calculated (A) standard deviation and (B) range of Velodyne® HDL–32E and Livox® Mid–40 over duration for all experiments.
Figure 36.
Distribution of precision (measurement range) for the (A) Velodyne® HDL–32E and (B) Livox® Mid–40 across their fields of view, (C) colorized by respective percentiles.
Figure 36.
Distribution of precision (measurement range) for the (A) Velodyne® HDL–32E and (B) Livox® Mid–40 across their fields of view, (C) colorized by respective percentiles.
Figure 37.
Accuracy of Velodyne® HDL–32E over time in night and day outdoor experiments. Shift in measured and “true” distance between night and day experiments is the result of minor adjustments made to scanner position after night iteration.
Figure 37.
Accuracy of Velodyne® HDL–32E over time in night and day outdoor experiments. Shift in measured and “true” distance between night and day experiments is the result of minor adjustments made to scanner position after night iteration.
Figure 38.
Amount of error observed in Livox® Mid–40 measurements in night and day scan conditions, by percentile.
Figure 38.
Amount of error observed in Livox® Mid–40 measurements in night and day scan conditions, by percentile.
Figure 39.
Application of error mitigation techniques on Velodyne® HDL–32E measurements.
Figure 39.
Application of error mitigation techniques on Velodyne® HDL–32E measurements.
Figure 40.
Applications of linear regressions on subsections of Velodyne® HDL–32E observations, split by scan azimuth.
Figure 40.
Applications of linear regressions on subsections of Velodyne® HDL–32E observations, split by scan azimuth.
Table 1.
Velodyne
® HDL–32E Select Specifications [
13].
Table 1.
Velodyne
® HDL–32E Select Specifications [
13].
| Platform |
|---|
| Overall Dimensions | 24.6 cm × 11.6 cm × 11.6 cm |
| Operating Temperature | −10 °C to +40 °C |
| Weight | 2.40 kg |
| Sensor |
| Laser Wavelength | 903 nm |
| Laser Classification | Class 1 Eye Safe |
| Channels | 32 |
| Measurement Range (min, max) | 1 m, 100 m |
| Measurement Range (resolution) | 0.002 m |
| Manufacturer’s Reported Range Accuracy | ±0.02 m |
| Measured Returns | 1 or 2 |
| Field of View (Vertical) | +10.67° to −30.67° (41.33°) |
| Field of View (Horizontal) | 360° |
| Angular Resolution (Vertical) | 1.33° |
| Angular Resolution (Horizontal/Azimuth) | 0.08°–0.33° |
| Beam Divergence | 3 mrad |
| Rotation Rate | 5 Hz to 20 Hz |
| 3D Lidar Data Points Generated: | |
| Single/Dual Return Mode | 695,000/1,390,000 points per second |
Table 2.
Livox
® Mid–40 Select Specifications [
15].
Table 2.
Livox
® Mid–40 Select Specifications [
15].
| Platform |
|---|
| Overall Dimensions | 8.8 cm × 7.6 cm × 6.9 cm |
| Operating Temperature | −20 °C to +65 °C |
| Weight | 760 g |
| Sensor |
| Laser Wavelength | 905 nm |
| Laser Classification | Class 1 (IEC 60825-1:2014) eye safe |
| Channels | 1 |
| Measurement Range (min) | 1 m |
| Measurement Range (max) | 90 m at 10% reflectivity |
| | 130 m at 20% reflectivity |
| | 260 m at 80% reflectivity |
| Manufacturer’s Reported Measurement Range (precision) (1 σ at 20 m) | 2 cm |
| Beam Divergence | 0.28° (vertical) × 0.03° (horizontal) |
| Measured Returns | 1 |
| Field of View (Circular) | 38.4° |
| Angular Accuracy | <0.1° |
| Point Generation Rate | 100,000 points per second |
Table 3.
Experiment List and Conditions.
Table 3.
Experiment List and Conditions.
| Lidar Scanner | Standoff Distance | Day/Night | Experiment Date |
|---|
| HDL–32E | 30 m | Day | 4 June 2021 |
| HDL–32E | 30 m | Night | 9 July 2021 |
| HDL–32E | 30 m | Day | 13 July 2021 |
| HDL–32E | 60 m | Night | 15 July 2021 |
| Mid–40 | 30 m | Night | 4 November 2021 |
| HDL–32E | 30 m | Night | 21 November 2021 * |
| Mid–40 | 30 m | Night | 21 November 2021 * |
| HDL–32E | 30 m | Day | 21 November 2021 * |
| Mid–40 | 30 m | Day | 21 November 2021 * |
Table 4.
Summary of Velodyne® HDL–32E indoor experiment indoor measurements (average of all points from each scanner within the −8° to +8° scan window).
Table 4.
Summary of Velodyne® HDL–32E indoor experiment indoor measurements (average of all points from each scanner within the −8° to +8° scan window).
| Scanner | Offset | Range (m) | St Dev (m) | Average (m) |
|---|
| 31 | 10.67° | 0.011 | 0.001 | 2.226 |
| 29 | 9.33° | 0.013 | 0.001 | 2.217 |
| 27 | 8.00° | 0.011 | 0.002 | 2.196 |
| 25 | 6.67° | 0.016 | 0.001 | 2.180 |
| 23 | 5.33° | 0.012 | 0.002 | 2.172 |
| 21 | 4.00° | 0.018 | 0.002 | 2.162 |
| 19 | 2.67° | 0.016 | 0.002 | 2.143 |
| 17 | 1.33° | 0.024 | 0.003 | 2.158 |
| 15 | 0.00° | 0.021 | 0.002 | 2.124 |
| 13 | −1.33° | 0.015 | 0.001 | 2.119 |
| 11 | −2.67° | 0.015 | 0.001 | 2.111 |
| 9 | −4.00° | 0.018 | 0.002 | 2.107 |
| 7 | −5.33° | 0.026 | 0.004 | 2.105 |
| 5 | −6.67° | 0.021 | 0.002 | 2.101 |
| 3 | −8.00° | 0.027 | 0.003 | 2.099 |
| 1 | −9.33° | 0.014 | 0.001 | 2.093 |
| 30 | −10.67° | 0.017 | 0.002 | 2.103 |
| 28 | −12.00° | 0.019 | 0.002 | 2.105 |
| 26 | −13.33° | 0.013 | 0.002 | 2.105 |
| 24 | −14.67° | 0.019 | 0.002 | 2.114 |
| 22 | −16.00° | 0.019 | 0.002 | 2.120 |
| 20 | −17.33° | 0.011 | 0.001 | 2.131 |
| 18 | −18.67° | 0.017 | 0.002 | 2.128 |
| 16 | −20.00° | 0.013 | 0.002 | 2.144 |
| 14 | −21.33° | 0.022 | 0.003 | 2.150 |
| 12 | −22.67° | 0.021 | 0.003 | 2.160 |
| 10 | −24.00° | 0.018 | 0.002 | 2.168 |
| 8 | −25.33° | 0.015 | 0.002 | 2.192 |
| 6 | −26.67° | 0.017 | 0.002 | 2.207 |
| 4 | −28.00° | 0.010 | 0.001 | 2.225 |
| 2 | −29.33° | 0.015 | 0.002 | 2.250 |
| 0 | −30.67° | 0.012 | 0.001 | 2.253 |
| Average | 0.017 | 0.002 | 2.151 |