The Regional Disparity of Urban Spatial Expansion Is Greater than That of Urban Socioeconomic Expansion in China: A New Perspective from Nighttime Light Remotely Sensed Data and Urban Land Datasets
Abstract
:1. Introduction
2. Study Area and Data Sources
2.1. Study Area
2.2. Data Sources and Data Processing
3. Methods
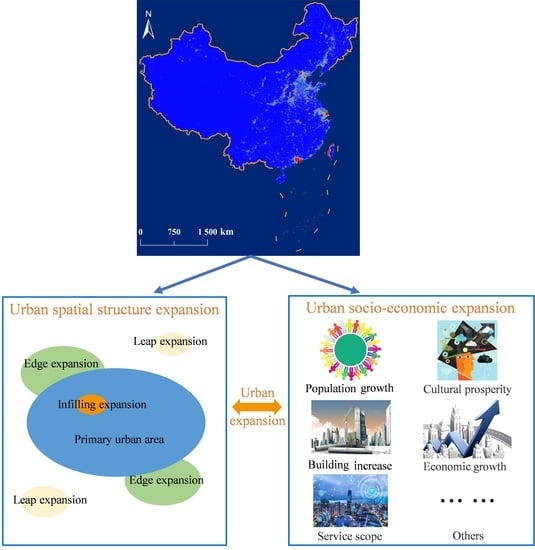
3.1. Defining Urban Expansion
3.2. Calculating Dagum Gini Coefficient
3.3. Stochastic Convergence Test
4. Results and Discussion
4.1. Accuracy Evaluation of Urban Expansion
4.2. Regional Disparity in Urban Expansion in China
4.3. Decomposition of Regional Disparity in Urban Expansion
4.4. Stochastic Convergence Test of Urban Expansion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, X.; Shi, P.; Liu, Y.J.N. Society: Realizing China’s urban dream. Nature 2014, 509, 158–160. [Google Scholar] [CrossRef]
- Gong, P.; Li, X.; Zhang, W.J.S.B. 40-Year (1978–2017) human settlement changes in China reflected by impervious surfaces from satellite remote sensing. Sci. Bull. 2019, 64, 756–763. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, Z.; Liu, F.; Zhao, X.; Wang, X.; Liu, B.; Hu, S.; Wen, Q.; Zuo, L.; Yi, L.; et al. City size distribution and its spatiotemporal evolution in China. Chin. Geogr. Sci. 2016, 26, 703–714. [Google Scholar] [CrossRef]
- United Nations. About the Sustainable Development Goals. 2016. Available online: https://www.un.org/sustainabledevelopment/sustainable-development-goals/ (accessed on 20 May 2021).
- Zhang, X.; Brandt, M.; Tong, X.; Ciais, P.; Yue, Y.; Xiao, X.; Zhang, W.; Wang, K.; Fensholt, R. A large but transient carbon sink from urbanization and rural depopulation in China. Nat. Sustain. 2022, 5, 321–328. [Google Scholar] [CrossRef]
- Zhao, J.; Xiao, Y.; Sun, S.; Sang, W.; Axmacher, J.C. Does China’s increasing coupling of ‘urban population’ and ‘urban area’ growth indicators reflect a growing social and economic sustainability? J. Environ. Manag. 2022, 301, 113932. [Google Scholar] [CrossRef]
- Shi, K.; Wu, Y.; Liu, S. Does China’s City-Size Distribution Present a Flat Distribution Trend? A Socioeconomic and Spatial Size Analysis From DMSP-OLS Nighttime Light Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5171–5179. [Google Scholar] [CrossRef]
- Du, P.; Hou, X.; Xu, H. Dynamic Expansion of Urban Land in China’s Coastal Zone since 2000. Remote Sens. 2022, 14, 916. [Google Scholar] [CrossRef]
- Bernt, M. The limits of shrinkage: Conceptual pitfalls and alternatives in the discussion of urban population loss. Int. J. Urban Reg. Res. 2016, 40, 441–450. [Google Scholar] [CrossRef]
- Liu, S.; Shen, J.; Liu, G.; Wu, Y.; Shi, K. Exploring the effect of urban spatial development pattern on carbon dioxide emissions in China: A socioeconomic density distribution approach based on remotely sensed nighttime light data. Comput. Environ. Urban Syst. 2022, 96, 101847. [Google Scholar] [CrossRef]
- Wu, Y.; Li, C.; Shi, K.; Liu, S.; Chang, Z. Exploring the effect of urban sprawl on carbon dioxide emissions: An urban sprawl model analysis from remotely sensed nighttime light data. Environ. Impact Assess. Rev. 2022, 93, 106731. [Google Scholar] [CrossRef]
- Li, X.; Gong, P.; Liang, L. A 30-year (1984–2013) record of annual urban dynamics of Beijing City derived from Landsat data. Remote Sens. Environ. 2015, 166, 78–90. [Google Scholar] [CrossRef]
- Liu, S.; Shi, K.; Wu, Y.; Chang, Z. Remotely sensed nighttime lights reveal China’s urbanization process restricted by haze pollution. Build. Environ. 2021, 206, 108350. [Google Scholar] [CrossRef]
- Shi, K.; Chang, Z.; Chen, Z.; Wu, J.; Yu, B. Identifying and evaluating poverty using multisource remote sensing and point of interest (POI) data: A case study of Chongqing, China. J. Clean. Prod. 2020, 255, 120245. [Google Scholar] [CrossRef]
- Chen, Z.; Wei, Y.; Shi, K.; Zhao, Z.; Wang, C.; Wu, B.; Qiu, B.; Yu, B. The potential of nighttime light remote sensing data to evaluate the development of digital economy: A case study of China at the city level. Comput. Environ. Urban Syst. 2022, 92, 101749. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, C.; Zhou, Y.; Li, X.; Shen, S.; Song, C. A global dataset of annual urban extents (1992–2020) from harmonized nighttime lights. Earth Syst. Sci. Data 2022, 14, 517–534. [Google Scholar] [CrossRef]
- Pandey, B.; Joshi, P.K.; Seto, K.C. Monitoring urbanization dynamics in India using DMSP/OLS night time lights and SPOT-VGT data. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 49–61. [Google Scholar] [CrossRef]
- Shi, K.; Yu, B.; Huang, Y.; Hu, Y.; Yin, B.; Chen, Z.; Chen, L.; Wu, J. Evaluating the ability of NPP-VIIRS nighttime light data to estimate the gross domestic product and the electric power consumption of China at multiple scales: A comparison with DMSP-OLS data. Remote Sens. 2014, 6, 1705–1724. [Google Scholar] [CrossRef]
- Liu, Z.; He, C.; Zhang, Q.; Huang, Q.; Yang, Y.J.L. Extracting the dynamics of urban expansion in China using DMSP-OLS nighttime light data from 1992 to 2008. Landsc. Urban Plan. 2012, 106, 62–72. [Google Scholar] [CrossRef]
- He, C.; Liu, Z.; Tian, J.; Ma, Q. Urban expansion dynamics and natural habitat loss in China: A multiscale landscape perspective. Glob. Change Biol. 2014, 20, 2886–2902. [Google Scholar] [CrossRef]
- Cao, X.; Chen, J.; Imura, H.; Higashi, O. A SVM-based method to extract urban areas from DMSP-OLS and SPOT VGT data. Remote Sens. Environ. 2009, 113, 2205–2209. [Google Scholar] [CrossRef]
- Wang, H.; Liu, G.; Shi, K. What Are the Driving Forces of Urban CO2 Emissions in China? A Refined Scale Analysis between National and Urban Agglomeration Levels. Int. J. Environ. Res. Public Health 2019, 16, 3692. [Google Scholar] [CrossRef] [PubMed]
- Shi, K.; Chen, Y.; Yu, B.; Xu, T.; Yang, C.; Li, L.; Huang, C.; Chen, Z.; Liu, R.; Wu, J. Detecting spatiotemporal dynamics of global electric power consumption using DMSP-OLS nighttime stable light data. Appl. Energy 2016, 184, 450–463. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, L.; Shi, P.; Ichinose, T. The Study on Urbanization Process in China Based on DMSP/OLS Data: Development of a Light Index for Urbanization Level Estimation. J. Remote Sens. 2003, 7, 168–175. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, H.; Yang, Q. An Empirical Analysis on China’s Regional Disparity of Brand Economic Development and Its Influencing Factors: Based on Dagum’s Gini Coefficient Decomposition Method and China’s 500 Most Valuable Brands from 2004 to 2011. Econ. Rev. 2012, 3, 57–65. [Google Scholar]
- Carlino, G.; Mills, L. Testing neoclassical convergence in regional incomes and earnings. Reg. Sci. Urban Econ. 1996, 26, 565–590. [Google Scholar] [CrossRef]
- Evans, P.; Karras, G. Convergence revisited. J. Monet. Econ. 1996, 37, 249–265. [Google Scholar] [CrossRef]
- Press, C.S. China Statistical Yearbook. 2016. Available online: http://www.stats.gov.cn/tjsj/ (accessed on 19 April 2021).
- Wu, Y.; Shi, K.; Chen, Z.; Liu, S.; Chang, Z. Developing Improved Time-Series DMSP-OLS-like Data (1992–2019) in China by Integrating DMSP-OLS and SNPP-VIIRS. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Yang, S. Research on Governance of Real Estate Bubble from the Perspective of National Economic Security. Manag. Obs. 2015, 29, 13–73. [Google Scholar]
- Tan, Z.; Zhao, L. A Historical Analysis of the Process of the Great-leap-forward Development of West China. J. Yunnan Univ. Natl. 2013, 30, 101–107. (In Chinese) [Google Scholar]
- Fang, C.; Zeng, Z.; Cui, N. The economic disparities and their spatio-temporal evolution in China since 2000. Geogr. Res. 2015, 34, 234–246. (In Chinese) [Google Scholar]
- Chen, Z.; Song, P. WTO entry and the development of Chinese cities in the era of globalization. Urban Plan. Overseas 2002, 5, 1–2. [Google Scholar]
- Min, J. The Effect of the SARS Illness on Tourism in Taiwan: An Empirical Study. Int. J. Manag. 2005, 22, 497. [Google Scholar]
- Lu, H.; Ou, X.; Li, X.; Ye, L.; Sun, D. Space-Time Analysis on the Regional Economic Inequality and Polarization in China. Econ. Geogr. 2013, 33, 15–21. [Google Scholar]
- Liang, Q.; Chen, Q.; Wang, R. Household Registration Reform, Labor Mobility and Optimization of the Urban Hierarchy. Soc. Sci. China 2015, 36, 130–151. [Google Scholar]
- Ye, C.; Sun, C.; Chen, L. New evidence for the impact of financial agglomeration on urbanization from a spatial econometrics analysis. J. Clean. Prod. 2018, 200, 65–73. [Google Scholar] [CrossRef]
- Zhao, K.; Li, P.; Zhang, A. Impact of quality of economic growth on expansion of land use for urban construction: Perspective from total factor productivity. J. Huazhong Agric. Univ. 2012, 2, 53–57. (In Chinese) [Google Scholar] [CrossRef]
- Yang, B.; Xu, T.; Shi, L. Analysis on sustainable urban development levels and trends in China’s cities. J. Clean. Prod. 2017, 141, 868–880. [Google Scholar] [CrossRef]
- Liu, H.; Du, G. Regional Inequality and Stochastic Convergence in China. J. Quant. Tech. Econ. 2017, 34, 43–59. [Google Scholar] [CrossRef]
- Liao, C.J.; Huang, J.; Sheng, L.; You, H.Y. Grey Correlation Analysis between Urban Built-up Area Expansion and Social Economic Factors: A Case Study of Hangzhou, China. Appl. Mech. Mater. 2012, 209–211, 1615–1619. [Google Scholar] [CrossRef]
- Choi, C.-Y. A Variable Addition Panel Test for Stationarity and Confirmatory Analysis; Mimeo Department of Economics, University of New Hampshire: Durham, NH, USA, 2002. [Google Scholar]











| Year | Overall Regional Disparity | Intra-Regional | Between Regions | Contribution Rate (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ER | NER | CR | WR | NER-ER | CR-ER | CR-NER | WR-ER | WR-NER | WR-CR | Gw | Gnb | Gt | ||
| 1993 | 0.785 | 0.772 | 0.617 | 0.61 | 0.747 | 0.823 | 0.794 | 0.623 | 0.86 | 0.696 | 0.698 | 30.486 | 51.845 | 17.669 |
| 1995 | 0.783 | 0.763 | 0.613 | 0.591 | 0.734 | 0.829 | 0.797 | 0.613 | 0.857 | 0.686 | 0.680 | 30.468 | 54.098 | 15.434 |
| 1996 | 0.773 | 0.75 | 0.548 | 0.582 | 0.725 | 0.806 | 0.793 | 0.573 | 0.854 | 0.657 | 0.671 | 30.312 | 55.061 | 14.627 |
| 1998 | 0.764 | 0.744 | 0.538 | 0.568 | 0.713 | 0.799 | 0.781 | 0.560 | 0.852 | 0.646 | 0.662 | 30.278 | 55.713 | 14.009 |
| 1999 | 0.758 | 0.734 | 0.540 | 0.557 | 0.702 | 0.797 | 0.776 | 0.556 | 0.846 | 0.638 | 0.650 | 30.158 | 56.307 | 13.535 |
| 2000 | 0.754 | 0.730 | 0.542 | 0.553 | 0.694 | 0.793 | 0.773 | 0.554 | 0.843 | 0.634 | 0.643 | 30.096 | 56.309 | 13.595 |
| 2001 | 0.753 | 0.726 | 0.546 | 0.551 | 0.693 | 0.797 | 0.777 | 0.555 | 0.837 | 0.634 | 0.638 | 30.031 | 56.094 | 13.876 |
| 2002 | 0.742 | 0.707 | 0.551 | 0.543 | 0.690 | 0.798 | 0.765 | 0.558 | 0.827 | 0.635 | 0.633 | 29.730 | 55.961 | 14.310 |
| 2003 | 0.734 | 0.691 | 0.551 | 0.54 | 0.688 | 0.805 | 0.754 | 0.565 | 0.821 | 0.634 | 0.631 | 29.458 | 56.422 | 14.121 |
| 2004 | 0.730 | 0.684 | 0.551 | 0.538 | 0.688 | 0.808 | 0.750 | 0.566 | 0.816 | 0.636 | 0.629 | 29.335 | 56.416 | 14.249 |
| 2005 | 0.727 | 0.678 | 0.554 | 0.538 | 0.685 | 0.807 | 0.744 | 0.569 | 0.812 | 0.636 | 0.627 | 29.252 | 56.406 | 14.341 |
| 2006 | 0.723 | 0.675 | 0.556 | 0.539 | 0.680 | 0.808 | 0.739 | 0.575 | 0.809 | 0.634 | 0.625 | 29.200 | 56.233 | 14.568 |
| 2007 | 0.721 | 0.671 | 0.556 | 0.543 | 0.677 | 0.809 | 0.736 | 0.579 | 0.807 | 0.633 | 0.626 | 29.134 | 56.229 | 14.637 |
| 2008 | 0.719 | 0.669 | 0.558 | 0.545 | 0.675 | 0.807 | 0.733 | 0.582 | 0.805 | 0.634 | 0.626 | 29.103 | 56.081 | 14.816 |
| 2009 | 0.712 | 0.660 | 0.560 | 0.544 | 0.670 | 0.798 | 0.727 | 0.579 | 0.799 | 0.630 | 0.623 | 28.982 | 55.873 | 15.145 |
| 2010 | 0.708 | 0.654 | 0.567 | 0.544 | 0.665 | 0.794 | 0.725 | 0.581 | 0.793 | 0.630 | 0.619 | 28.890 | 55.654 | 15.456 |
| 2012 | 0.681 | 0.629 | 0.572 | 0.520 | 0.634 | 0.781 | 0.698 | 0.575 | 0.759 | 0.620 | 0.588 | 28.630 | 54.740 | 16.630 |
| 2015 | 0.670 | 0.619 | 0.565 | 0.512 | 0.623 | 0.776 | 0.686 | 0.573 | 0.746 | 0.612 | 0.579 | 28.543 | 54.365 | 17.092 |
| Year | Overall Regional Disparity | Intra-Regional | Between Regions | Contribution Rate (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ER | NER | CR | WR | NER-ER | CR-ER | CR-NER | WR-ER | WR-NER | WR-CR | Gw | Gnb | Gt | ||
| 1993 | 0.677 | 0.679 | 0.609 | 0.555 | 0.645 | 0.682 | 0.701 | 0.607 | 0.733 | 0.646 | 0.609 | 28.806 | 38.895 | 32.299 |
| 1995 | 0.664 | 0.656 | 0.599 | 0.538 | 0.605 | 0.680 | 0.697 | 0.589 | 0.721 | 0.618 | 0.580 | 28.769 | 42.785 | 28.446 |
| 1996 | 0.651 | 0.648 | 0.532 | 0.524 | 0.593 | 0.644 | 0.696 | 0.555 | 0.718 | 0.590 | 0.566 | 28.687 | 44.600 | 26.713 |
| 1998 | 0.638 | 0.636 | 0.519 | 0.491 | 0.588 | 0.634 | 0.678 | 0.529 | 0.711 | 0.578 | 0.551 | 28.610 | 45.012 | 26.378 |
| 1999 | 0.627 | 0.620 | 0.517 | 0.479 | 0.575 | 0.630 | 0.672 | 0.522 | 0.698 | 0.565 | 0.537 | 28.484 | 45.558 | 25.958 |
| 2000 | 0.624 | 0.618 | 0.527 | 0.476 | 0.561 | 0.627 | 0.673 | 0.531 | 0.691 | 0.565 | 0.528 | 28.406 | 45.537 | 26.056 |
| 2001 | 0.625 | 0.617 | 0.529 | 0.476 | 0.553 | 0.632 | 0.680 | 0.533 | 0.686 | 0.558 | 0.523 | 28.405 | 46.498 | 25.098 |
| 2002 | 0.618 | 0.605 | 0.529 | 0.465 | 0.550 | 0.638 | 0.672 | 0.519 | 0.680 | 0.550 | 0.516 | 28.337 | 46.515 | 25.149 |
| 2003 | 0.621 | 0.602 | 0.536 | 0.463 | 0.542 | 0.657 | 0.674 | 0.515 | 0.685 | 0.546 | 0.509 | 28.300 | 47.366 | 24.334 |
| 2004 | 0.619 | 0.596 | 0.534 | 0.465 | 0.542 | 0.662 | 0.675 | 0.512 | 0.681 | 0.542 | 0.511 | 28.241 | 47.559 | 24.200 |
| 2005 | 0.617 | 0.592 | 0.538 | 0.466 | 0.542 | 0.662 | 0.672 | 0.514 | 0.677 | 0.544 | 0.511 | 28.202 | 47.328 | 24.470 |
| 2006 | 0.612 | 0.587 | 0.537 | 0.463 | 0.542 | 0.663 | 0.666 | 0.511 | 0.668 | 0.543 | 0.510 | 28.190 | 46.556 | 25.255 |
| 2007 | 0.608 | 0.582 | 0.536 | 0.466 | 0.538 | 0.661 | 0.662 | 0.512 | 0.662 | 0.541 | 0.509 | 28.140 | 46.030 | 25.830 |
| 2008 | 0.606 | 0.580 | 0.534 | 0.469 | 0.537 | 0.659 | 0.659 | 0.512 | 0.658 | 0.539 | 0.510 | 28.145 | 45.535 | 26.320 |
| 2009 | 0.598 | 0.571 | 0.530 | 0.466 | 0.534 | 0.644 | 0.655 | 0.510 | 0.646 | 0.536 | 0.508 | 28.037 | 45.303 | 26.660 |
| 2010 | 0.592 | 0.566 | 0.529 | 0.463 | 0.529 | 0.641 | 0.651 | 0.507 | 0.634 | 0.533 | 0.505 | 28.018 | 45.220 | 26.762 |
| 2012 | 0.567 | 0.539 | 0.516 | 0.439 | 0.509 | 0.626 | 0.626 | 0.489 | 0.604 | 0.519 | 0.487 | 27.781 | 45.386 | 26.834 |
| 2015 | 0.550 | 0.528 | 0.503 | 0.429 | 0.492 | 0.618 | 0.601 | 0.477 | 0.583 | 0.506 | 0.470 | 27.852 | 43.802 | 28.347 |
| Region | USS | USE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IPS | Prob | Hadri | Prob | CA Result | IPS | Prob | Hadri | Prob | CA Result | |
| All cities | −0.980 | 0.164 | 18.629 | 0.000 | Ⅱ | −0.5930 | 0.267 | 10.865 | 0.000 | Ⅱ |
| NER | −1.331 | 0.129 | 3.467 | 0.001 | Ⅱ | −0.122 | 0.452 | 3.873 | 0.000 | Ⅱ |
| ER | 0.046 | 0.518 | 7.909 | 0.000 | Ⅱ | 1.338 | 0.910 | 7.687 | 0.000 | Ⅱ |
| CR | −0.559 | 0.288 | 3.124 | 0.001 | Ⅱ | −1.223 | 0.111 | 2.684 | 0.004 | Ⅱ |
| WR | −0.663 | 0.254 | 6.542 | 0.000 | Ⅱ | −1.282 | 0.099 | 6.214 | 0.000 | Ⅱ |
| Province | USS | USE | ||
|---|---|---|---|---|
| ADF | KPSS | ADF | KPSS | |
| Anhui | −3.206 | 0.093 | −4.314 ** | 0.089 |
| Beijing | −1.648 | 0.194 ** | −1.520 | 0.164 ** |
| Chongqing | −3.221 | 0.080 | −2.883 | 0.076 |
| Fujian | −0.686 | 0.188 ** | −1.212 | 0.188 ** |
| Guangdong | −4.134 ** | 0.186 ** | −2.052 | 0.184 ** |
| Gansu | −1.168 | 0.138 * | −2.812 | 0.163 ** |
| Guangxi | −4.308 ** | 0.068 | −2.847 | 0.104 |
| Guizhou | −3.023 | 0.094 | −3.570 * | 0.072 |
| Hebei | −2.897 | 0.147 ** | −3.147 | 0.091 |
| Henan | −0.680 | 0.175 ** | −1.374 | 0.175 ** |
| Heilongjiang | −3.422 * | 0.160 ** | −2.351 | 0.159 ** |
| Hainan | −2.343 | 0.132 * | −2.097 | 0.126 * |
| Hubei | −1.525 | 0.170 ** | −3.31 ** | 0.144 * |
| Hunan | −1.898 | 0.119 * | −2.291 | 0.120 * |
| Jilin | −2.124 | 0.152 ** | −2.286 | 0.160 ** |
| Jiangsu | −1.363 | 0.151 ** | −0.607 | 0.142 * |
| Jiangxi | −1.823 | 0.113 | −1.979 | 0.108 |
| Liaoning | −2.721 | 0.123 * | −2.055 | 0.161 ** |
| Inner Mongolia | −2.176 | 0.100 | −1.944 | 0.106 |
| Ningxia | −3.325 * | 0.069 | −2.124 | 0.119 * |
| Qinghai | −2.750 | 0.178 ** | −3.826 ** | 0.109 |
| Sichuan | −1.492 | 0.129 * | −1.835 | 0.120 * |
| Shaanxi | −2.068 | 0.107 | −3.269 * | 0.090 |
| Shandong | −1.453 | 0.154 ** | −1.026 | 0.161 ** |
| Shanghai | −2.305 | 0.180 ** | −1.228 | 0.177 ** |
| Shanxi | −4.761 *** | 0.076 | −2.234 | 0.104 |
| Tianjin | −3.284 * | 0.103 | −2.991 | 0.086 |
| Xinjiang | −1.878 | 0.069 | −2.571 | 0.119 * |
| Tibet | −1.313 | 0.174 ** | −1.697 | 0.167 ** |
| Yunnan | −0.871 | 0.155 ** | −0.706 | 0.159 ** |
| Zhejiang | −1.168 | 0.176 ** | −1.355 | 0.176 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Z.; Liu, S.; Wu, Y.; Shi, K. The Regional Disparity of Urban Spatial Expansion Is Greater than That of Urban Socioeconomic Expansion in China: A New Perspective from Nighttime Light Remotely Sensed Data and Urban Land Datasets. Remote Sens. 2022, 14, 4348. https://doi.org/10.3390/rs14174348
Chang Z, Liu S, Wu Y, Shi K. The Regional Disparity of Urban Spatial Expansion Is Greater than That of Urban Socioeconomic Expansion in China: A New Perspective from Nighttime Light Remotely Sensed Data and Urban Land Datasets. Remote Sensing. 2022; 14(17):4348. https://doi.org/10.3390/rs14174348
Chicago/Turabian StyleChang, Zhijian, Shirao Liu, Yizhen Wu, and Kaifang Shi. 2022. "The Regional Disparity of Urban Spatial Expansion Is Greater than That of Urban Socioeconomic Expansion in China: A New Perspective from Nighttime Light Remotely Sensed Data and Urban Land Datasets" Remote Sensing 14, no. 17: 4348. https://doi.org/10.3390/rs14174348
APA StyleChang, Z., Liu, S., Wu, Y., & Shi, K. (2022). The Regional Disparity of Urban Spatial Expansion Is Greater than That of Urban Socioeconomic Expansion in China: A New Perspective from Nighttime Light Remotely Sensed Data and Urban Land Datasets. Remote Sensing, 14(17), 4348. https://doi.org/10.3390/rs14174348