We compare our methods with several state-of-the-art methods: the SVM applied to spectral data [
17], the SVM applied to contextual data (CSVM) [
50], the spectral dictionary learning (SDL) [
12], the simultaneous orthogonal matching pursuit (SOMP) [
14], the spatial-aware dictionary learning (SADL) [
13], the generalized tensor regression (GTR) [
58], HybridSN [
22], ASTDL-CNN [
61] and SpectralFormer [
32]. Among these methods, SVM, CSVM, SDL, and SADL belong to SVM-based methods. Simultaneously, SDL, SADL, SOMP, and ASTDL-CNN are sparse representation methods. HybridSN, ASTDL-CNN, and SpectralFormer belong to neural network methods. The proposed TDSL extracts features by sparse representation and classifies features with SVM, thus we compare it with both SVM-based methods and sparse representation methods. To demonstrate the effectiveness of feature extractors trained from other unlabeled data, we compare TDSL with SVM. CSVM is an improved SVM method. To demonstrate the effectiveness of dictionary learning in TDSL, we compare it with SDL and SADL. SDL is a spectral-based method, and SADL incorporates spectral information with spatial information. SOMP is a sparse representation method without the SVM classifier. It is worth comparing our methods with GTR because GTR utilizes tensor technology and it is necessary to compare our methods with neural network methods and our previous works. The codes of SVM, CSVM, SDL, SOMP, and SADL are available on the website (
http://ssp.dml.ir/research/sadl/ (accessed on 7 May 2020)), the codes of GTR are available on the website (
https://github.com/liuofficial/GTR (accessed on 25 July 2022)), the codes of HybridSN are available on the website (
https://github.com/MVGopi/HybridSN (accessed on 25 July 2022)), and the codes of SpectralFormer are available on the website (
https://github.com/danfenghong/IEEE_TGRS_SpectralFormer (accessed on 12 August 2022)).
For our proposed methods, the new number of spectral bands
B is set to 50 for all experiments [
60]. Ref. [
60] demonstrates when B is larger than 40, the information preserved by PCA is sufficient to achieve high classification accuracy. The size of the extracted samples is set to
(i.e.,
P is set to 7, which is the same as in [
32]). Ref. [
65] demonstrates the K-HOSVD can achieve convergence in about 5 iterations. Therefore, the maximum number of iterations for updating dictionaries in Algorithm 1 is set to 10 to guarantee convergence. Ref. [
67] states when tolerance
, a sparse representation is correctly recovered. Moreover, the higher precision required, the smaller tolerance and more training time are needed. In our method, the tolerance
in the NBOMP algorithm is set as
. The SVM used in the proposed methods is performed by using the radial basis function (RBF) kernel. In SVM, RBF-kernel parameter
and regularization parameter
C can be optimally determined by five-fold cross-validation on the training set in the range of
and
.
4.1. Data Sets Description
The five representative HSI data sets used in this paper are briefly described as follows.
Figure 2 shows the composite three-band false-color maps, the ground truth maps, and the details of the samples for Salinas, Pavia Center, Indian Pines, and Pavia University.
Table 3 shows the information of the Houston2013 dataset.
We first introduce the data sets used as unlabeled data sets, i.e., data set #1.
(1) Salinas: This data set is collected by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor over Salinas Valley in California. The HSI consists of
pixels with a spatial resolution of
meters per pixel. The AVIRIS gathers 224 bands in the wavelength range 0.4–2.5
m, whereas we remove 20 bands, which are noisy or cover the water absorption region. Therefore, we use 204 spectral bands in the experiments. The ground truth of Salinas contains 16 classes, including bare soils, vegetables, and vineyard fields. The details of these classes are displayed in the corresponding table in
Figure 2. We use
samples of every class as the unlabeled samples to train feature extractors.
(2) Pavia Center: This data set is gathered by the Reflective Optics Spectrometer (ROSIS) over Pavia in northern Italy. The HSI consists of
pixels, and the spatial resolution is
meters per pixel. The ROSIS sensor captures 115 bands with a spectral range of 0.43–0.86
m. The number of spectral bands is 102 after removing the noisy bands. The ground truth contains 9 classes, and the detailed information of every class is shown in the corresponding table in
Figure 2. We randomly choose 200 samples from every class as the unlabeled samples to train feature extractors.
Next, we introduce the data sets used as labeled training data and testing data, i.e., data set #2.
(1) Indian Pines: This data set is collected by the AVIRIS sensor over the Indian Pines in Northwestern Indiana. The scene consists of
pixels, and the spatial resolution is 20 meters per pixel. We preserve 200 bands after removing noisy bands in the experiments. The ground truth contains 16 classes, including agriculture, forest, and natural perennial vegetation. The details of the information, including the name of every class, the numbers of training samples, and the numbers of testing samples, are displayed in the corresponding table in
Figure 2. The number of training samples accounts for about
of the total samples with annotation.
(2) Pavia University: This data set is gathered by the ROSIS sensor surrounding the university of Pavia. The image consists of
pixels, and the number of spectral bands for the experiments is 103. The spatial resolution is the same as the Pavia Center. The ground truth contains 9 classes, and the classes are different from the classes of Pavia Center. The details of every class are displayed in the corresponding table in
Figure 2. We randomly choose 300 or 400 samples from every class as the labeled training samples, and the total proportion is less than
.
Finally, we introduce the Houston2013 dataset. This data set is gathered by the ITRES CASI-1500 sensor over the campus of the University of Houston and its neighboring rural areas in the USA. The image consists of
pixels and 144 bands with a spectral range of 0.364–1.046
m. The ground truth contains 15 classes. The details of every class are displayed in
Table 3, whose background colors indicate different classes of land-covers, and the numbers of training samples are set according to [
32].
4.2. Influence of the Sparsity Levels
In the proposed TDSL classification method, there are two sparsity level parameters, one is in Equation (
26) to train feature extractors on data set #1 via the STDL algorithm, and the other one is in Equations (
27) and (
28) to extract tensor features on data set #2 via the NBOMP algorithm. Equations (
26)–(
28) show that the sparsity level parameters decide the number of nonzero coefficients in feature tensors, and the number of nonzero coefficients in feature tensors is also related to the size of the input data. The number of nonzero coefficients in feature tensors affects the classification accuracy. Therefore, the sparsity level parameters are selected according to the size of the input data and ensure that the number of nonzero coefficients in each feature tensor is enough. We suggest that the number of nonzero coefficients in each feature tensor should be over 20. In this study, we analyze the impacts of the two sparsity level parameters
and
according to the experiment results of methods: TDSL-S on the Indian Pines data set, TDSL-P on the Indian Pines, TDSL-S on Pavia University, and TDSL-P on Pavia University. The numbers of training samples in the two data sets and the numbers of testing samples in data set #2 are set as
Figure 2. The results are displayed in
Figure 3. In
Figure 3, the red dots are the actual experiment results, and the three-dimensional surfaces are fitted according to these red dots. The surfaces can clearly show the influence of the sparsity level parameters on classification results. We evaluate the sparsity level parameters by the OA, AA, and Kappa. Furthermore, the actual number of nonzero coefficients in the sparse feature tensor for every sample in data set #2 is denoted as
K, and the average
K for the whole data set #2 is also displayed in
Figure 3.
Figure 3 shows the variation of classification accuracies with the two sparsity level parameters
and
. Moreover,
,
together decide the actual numbers of nonzero coefficients in tensor features
K, and affect the classification results. Furthermore, for different data set #2, the variation tendency is different. The first row and the second row from top to bottom indicate the results on Indian Pines, i.e., data set #2 is the Indian Pines in the experiments. The third row and the fourth row indicate the results on Pavia University, i.e., data set #2 is the Pavia University in the experiments. The first row and the second row have a similar variation tendency, the third row and the fourth row also have a similar variation tendency.
Figure 3a–h show that OA, AA, and Kappa of TDSL-S and TDSL-P on Indian Pines increase with the decrease in
, while
K decreases with the decrease in
, when
is fixed. Moreover, when
is fixed, with the change of
, the OA, AA, Kappa, and
K remain the same or fluctuate within a certain range.
Figure 3i–p show that the OA, AA, and Kappa of TDSL-S and TDSL-P on Pavia University increase first and then fluctuate within a certain range, with the increase in
when
is fixed. Moreover, when
is fixed, the OA, AA, Kappa increase first and then fluctuate within a certain range with the increase in
.
According to
Figure 3, it is obvious that the classification accuracies are affected by both
and
. Furthermore,
Figure 4,
Figure 5,
Figure 6 and
Figure 7 display the classification accuracies and
K are affected by
or
when the other one is fixed.
Figure 4 shows the results of TDSL-S on Indian Pines, and
Figure 5 shows the results of TDSL-P on Indian Pines.
Figure 4a and
Figure 5a show that
K remains the same and accuracies fluctuate within a certain range when
is fixed.
Figure 4b and
Figure 5b shows that accuracies increase first and then decrease with the increase in
when
is fixed and
K increases with the increase in
.
Figure 6 shows the results of TDSL-S on Pavia University, and
Figure 7 shows the results of TDSL-P on Pavia University.
Figure 6a and
Figure 7a show that accuracies increase first and then fluctuate within a certain range with the increase in
when
is fixed and
K increases step by step with the increase in
.
Figure 6b and
Figure 7b show that accuracies increase first and then fluctuate within a certain range with the increase in
when
is fixed. Moreover,
K increases first and then remains the same with the increase in
when
is fixed.
For all the experiments, the classification accuracies are related to the average
K. The classification accuracies increase with the increase in the average
K, at first. It is because the average
K represents the number of features in the sparse feature tensor. When the number of features is small, the information represented by these features is not enough to classify. Whereas, when the average
K is larger than a certain value, the classification accuracies fluctuate in a certain range or decrease. It is because when the number of features is large enough, the information is enough for classification. The fluctuation is due to noise and the SVM model. However, if there are too many features, the classifier will be difficult to classify. The average
K is related to the two sparsity level parameters
,
, and the error of the least-squares optimization problem Equations (
26)–(
28). For different data set #2, the satisfied optimization termination conditions of NBOMP are different. For Indian Pines, when the number of nonzero coefficients gets to
, the optimization of sparse representation stops. Therefore, in
Figure 3d,h,
Figure 4b and
Figure 5b, the
K increases with the increase in
. Whereas the influence of
on
K is small. For Pavia University, the error of sparse representation satisfies the conditions for loop termination, before the number of nonzero coefficients gets to
. In this case, the
decides the maximum of
K, and the
decides the actual number of
K. When the
is smaller than
, the average
K increases with the increase in
first but when the
gets to
, the average
K keeps the same, despite the
continuing to increase. This phenomenon is obvious in
Figure 3l,p,
Figure 6b and
Figure 7b.
According to these experiment results, we determine the parameters. The two sparsity level parameters in the experiments for the two data sets are set as in
Table 4.
4.5. Comparisons with Different Classification Methods
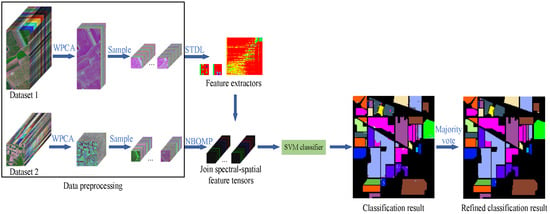
We evaluate the proposed methods by comparing them with the aforementioned methods on two wildly used data sets (the Indian Pines, and the Pavia University). Moreover, the two data sets correspond to data set #2 in our proposed methods. When we train feature extractors on the data set Salinas (i.e., data set #1 is the salinas), the methods are denoted with ‘-S’, and when data set #1 is the Pavia Center, the methods are denoted with ‘-P’. We evaluate the proposed TDSL and TDSLMV at the same time. To demonstrate that the proposed methods are effective in the cross-scene classification, we perform TDSL-S, TDSLMV-S on the Indian Pines data, and perform TDSL-P, TDSLMV-P on the Pavia data, where data set #1 and data set #2 are gathered by the same sensor but over different scenes. Furthermore, to demonstrate that the proposed methods can work in the cross-scene and cross-sensor classification, we perform TDSL-S, TDSLMV-S on Pavia University, and perform TDSL-P, TDSLMV-P on the Indian Pines, where the data set #1 and data set #2 are gathered by different sensors over difference scenes.
We perform the experiments with randomly extracted samples ten times for every method, and the numbers of training samples and testing samples are as shown in
Figure 2. The classification results for the Indian Pines data are reported in
Table 5. We report the results in the form of ‘mean value ± standard deviation’.
Table 5 shows that SVM and SDL obtain poor results since they just utilize spectral data. SpectralFormer obtains better results than SVM and SDL, although the input of SpectralFormer is also spectral data. It demonstrates the superiority of neural network methods. CSVM gets better results than SVM, and SADL obtains better results than SDL, which demonstrates that contextual information is important for HSI classification. SOMP provides worse results than SADL, though they are both sparse representation methods applied to both spectral and contextual data. This implies that training dictionaries from training samples and classifying the corresponding sparse coefficients by SVM can improve the classification. Furthermore, SVM can not only give the classification results but also can extract further features from the sparse coefficients. GTR provides better results than other methods except for the proposed methods, this stresses that the tensor technology is more beneficial to the HSI classification. The results of HybridSN are better than SVM, CSVM, SDL, SOMP, SADL, and SpectralFormer, because HybridSN extracts spectral-spatial features by 3-D CNN and 2-D CNN. ASTDL-CNN obtains better results than HybridSN, because ASTDL can extract intrinsic tensor features, which are more conducive to classification. HybridSN and ASTDL-CNN are CNN-based methods and need more labeled data than GTR, therefore, the results of GTR are better than those of HybridSN and ASTDL-CNN. The results of TDSL-S are better than those of SVM, which demonstrates that the feature extractors learned from another unlabeled data set can extract discriminative features for classification. The results of TDSL-P demonstrate that the proposed method can provide very high classification accuracies even meeting the cross-scene and cross-sensor task. TDSLMV-S provides the best results in terms of the OA, AA, and Kappa. The OA of TDSLMV-S achieves as high as
, and even the OA of TDSLMV-P achieves as high as
in cross-scene and cross-sensor classification tasks. Compared with GTR, the average OA of TDSLMV-S is improved by
. Furthermore, the standard deviations are small which means that the proposed methods are robust.
Figure 9 illustrates the classification maps obtained by the thirteen aforementioned methods for the Indian Pines. It can be easily observed that many isolated misclassified pixels appear in the classification maps of the spectral methods SVM, SDL, and SpectralFormer. From
Figure 9b,d,e we can easily observe that the utilization of contextual information can effectively reduce the isolated misclassified pixels. From
Figure 9g,h,j–m, we can observe that very few isolated misclassified pixels appear in the classification maps of the tensor-based methods (GTR, HybridSN, ASTDL-CNN, and our methods). However, the misclassified pixels are more likely to appear together in the classification maps for tensor-based methods. Especially, the misclassified pixels appear at the edges between two different homogenous regions.
Figure 9g,h show that the misclassified pixels tend to appear in small homogenous regions. This is because the tensor samples may contain pixels belonging to different classes, especially when extracting samples at the edges between different homogenous regions.
Figure 9l,m show that the majority vote can refine the classification, correcting most of the misclassified pixels in the large homogenous regions and at the edges of different homogenous regions. Therefore, the classification map of TDSLMV-S is the most similar to the ground truth map of the Indian Pines.
Table 5.
Classification accuracies (Mean Value ± Standard Deviation %) of different methods for the Indian Pines data set, bold values indicate the best result for a row.
Table 5.
Classification accuracies (Mean Value ± Standard Deviation %) of different methods for the Indian Pines data set, bold values indicate the best result for a row.
| CLASS | SVM [17] | CSVM [50] | SDL [12] | SOMP [14] | SADL [13] | GTR [58] | HybridSN [22] | ASTDL-CNN [61] | SpectralFormer [32] | TDSL-S | TDSL-P | TDSLMV-S | TDSLMV-P |
|---|
| 1 | | | | | | | | | | | | | |
| 2 | | | | | | | | | | | | | |
| 3 | | | | | | | | | | | | | |
| 4 | | | | | | | | | | | | | |
| 5 | | | | | | | | | | | | | |
| 6 | | | | | | | | | | | | | |
| 7 | | | | | | | | | | | | | |
| 8 | | | | | | | | | | | | | |
| 9 | | | | | | | | | | | | | |
| 10 | | | | | | | | | | | | | |
| 11 | | | | | | | | | | | | | |
| 12 | | | | | | | | | | | | | |
| 13 | | | | | | | | | | | | | |
| 14 | | | | | | | | | | | | | |
| 15 | | | | | | | | | | | | | |
| 16 | | | | | | | | | | | | | |
| OA | | | | | | | | | | | | | |
| AA | | | | | | | | | | | | | |
| Kappa | | | | | | | | | | | | | |
The classification results for Pavia University are reported in
Table 6, and the corresponding classification maps are illustrated in
Figure 10. The results of HybridSN and ASTDL-CNN are better than CSVM, SOMP, SADL, and GTR, and the results of SpectralFormer are better than SVM and SDL. It demonstrates that neural network-based methods can achieve better results when the labeled samples are enough. The results of TDSL-S are higher than the comparison methods, which means the proposed method is superior to the other methods even for the cross-scene and cross-sensor classification tasks. Moreover, TDSLMV-P provides the highest accuracies in terms of the OA, AA, and Kappa. The average OA of TDSLMV-P achieves
, which is very high in all methods for HSI classification. Even for the cross-scene and cross-sensor classification, the average OA of TDSLMV-S achieves as high as
. Compared with ASTDL-CNN, the average OA of TDSLMV-P is improved by
. Furthermore, the standard deviations of OA, AA, and Kappa, for our proposed methods (i.e., TDSL-S, TDSL-P, TDSLMV-S, TDSLMV-P) are smaller than those for the other methods. This further demonstrates the robustness of our methods.
Figure 10 illustrates the classification maps and the corresponding error maps for the aforementioned methods. Unlike the Indian Pines, Pavia University consists of many small homogenous regions, which means that Pavia University contains more edge. Therefore, the performance of GTR on Pavia University data is worse than it on Indian Pines data.
Figure 10a,c,i show that the misclassified pixels for spectral methods appear not only at the edges but also in the large homogenous regions. From
Figure 10b,e, we can infer that the utilization of contextual information can reduce the misclassified pixels in large homogenous regions. Furthermore, the misclassified pixels for tensor-based methods mainly appear at the edges and in the small homogenous regions, which is observed from
Figure 10f–h,j,k. However,
Figure 10j,m show that the majority vote can also correct the misclassified pixels at edges and in the little homogenous regions.
Table 6.
Classification accuracies (Mean Value ± Standard Deviation %) of different methods for the Pavia University data set, bold values indicate the best result for a row.
Table 6.
Classification accuracies (Mean Value ± Standard Deviation %) of different methods for the Pavia University data set, bold values indicate the best result for a row.
| CLASS | SVM [17] | CSVM [50] | SDL [12] | SOMP [14] | SADL [13] | GTR [58] | HybridSN [22] | ASTDL-CNN [61] | SpectralFormer [32] | TDSL-S | TDSL-P | TDSLMV-S | TDSLMV-P |
|---|
| 1 | | | | | | | | | | | | | |
| 2 | | | | | | | | | | | | | |
| 3 | | | | | | | | | | | | | |
| 4 | | | | | | | | | | | | | |
| 5 | | | | | | | | | | | | | |
| 6 | | | | | | | | | | | | | |
| 7 | | | | | | | | | | | | | |
| 8 | | | | | | | | | | | | | |
| 9 | | | | | | | | | | | | | |
| OA | | | | | | | | | | | | | |
| AA | | | | | | | | | | | | | |
| Kappa | | | | | | | | | | | | | |
To discuss the performance of the proposed methods when meeting the cross-scene and cross-sensor classification tasks, we display the OA of the proposed methods on the two data sets in
Figure 11. It can be easily observed that on the Indian Pines data, TDSL-S and TDSLMV-S provide higher OA than TDSL-P and TDSLMV-P, respectively. Whereas, on the Pavia University data, the accuracies of TDSL-P and TDSLMV-P are higher than those of TDSL-S and TDSLMV-S, respectively. This means that the proposed methods provide higher accuracies for the cross-scene task than for the cross-scene and cross-sensor tasks. Furthermore, applying the majority vote not only can refine the classification results, but also close the gaps of accuracies caused by cross-sensor.
To evaluate the impact of different amounts of labeled training samples from data set #2, we perform all the proposed methods three times with
,
,
,
,
, and
training samples of the labeled data. We illustrate the results in
Figure 12. In
Figure 12a, the accuracies with
and
labeled training samples are not very high on Indian Pines data. Because some classes contain very few samples, for
, the numbers of labeled training samples in some classes are less than five. However, when the number of labeled training samples gets over
, the accuracies of TDSLMV are more than
. In
Figure 12b, the accuracies of TDSLMV with
labeled training samples can obtain
on Pavia University. This demonstrates that our proposed methods can work well with a small labeled training set.
To evaluate the impact of different amounts of unlabeled training samples from data set #1, we perform the proposed TDSL and TDSLMV three times with
,
,
, and
training samples from the unlabeled data set Salinas, and we perform classification on Pavia University to evaluate the performance of the feature extractors in cross-scene and cross-sensor classification task.
Figure 13 displays the results. The accuracies with
unlabeled training samples from Salinas are not very high, the OA of TDSL-S is about
, and the OA of TDSLMV-S is lower than
. This demonstrates that when the amount of unlabeled samples is too small, the trained feature extractors can not extract effective generalization features but the accuracies with
unlabeled training samples from Salinas are very high, and the number of unlabeled training samples is about 1000. This demonstrates that at least a thousand unlabeled samples are needed to train the feature extractors.
We report the time of the aforementioned methods in
Table 7. It is easily observed that SVM is the fastest among these methods, CSVM and GTR are the second-fastest methods. The speeds of SDL, SADL, and ASTDL-CNN are slower than SVM, CSVM, and GTR, because the dictionary learning and sparse representation methods need more time. In SOMP, testing samples are sparsely represented by training samples directly, therefore, it does not need training time. In general, neural network methods need much time to train the model, therefore, the training time of HybridSN is the longest. SpectralFormer needs less training time than HybridSN and ASTDL-CNN, because the input of SpectralFormer is the spectrum, and the number of parameters in the model is small. The training time of ASTDL-CNN is shorter than HybridSN, because ASTDL simplifies the 2-D CNN. The proposed methods take the most time except HybridSN and ASTDL-CNN. The training time of TDSL and TDSLMV includes the time of training dictionaries, the time of sparse representation for labeled training samples, and the time of training SVM. The testing time of TDSL includes the time of sparse representation for testing samples and the time of classification with SVM. The testing time of TDSLMV includes the extra time of the majority vote than TDSL. Although the proposed methods are not the fastest, they provide high accuracies and can complete the cross-scene and cross-sensor classification tasks. Therefore, for applications that are not time critical the proposed methods have distinct advantages.
According to the above experimental results and analysis, the proposed TDLSMV achieves the highest classification accuracies, including the OA, AA, and Kappa, on both Indian Pines and Pavia University in all compared methods. Additionally, the standard deviations of TDSL and TDSLMV are smaller than the other compared methods. It demonstrates the robustness of the proposed methods. Furthermore, TDSL and TDSLMV can achieve high accuracies with a small labeled training set. The disadvantage of the proposed TDSL and TDSLMV is that their speeds are not the fastest.
4.6. Application on a Complex Dataset
We evaluate the classification performance of the trained feature extractor model applied to the Houston2013 dataset directly. The trained feature extractor models come from the aforementioned comparison experiments, in which the feature extractor models are trained on Salinas and Pavia Center data, and the parameters
and
are set as those in experiments on Indian Pines and Pavia University data, i.e.,
and
are set as in
Table 4. We just use the Houston2013 data to retrain the SVM model, because it is necessary for a classification task. Further, the window size of the majority vote is set as
, which is the same as in experiments on Pavia University data.
Table 7.
Speeds (Seconds) of different methods on the two data sets (the Indian Pines and the Pavia University).
Table 7.
Speeds (Seconds) of different methods on the two data sets (the Indian Pines and the Pavia University).
| Data Set | SVM [17] | CSVM [50] | SDL [12] | SOMP [14] | SADL [13] | GTR [58] | HybridSN [22] | ASTDL-CNN [61] | SpectralFormer [32] | TDSL-S | TDSL-P | TDSLMV-S | TDSLMV-P |
|---|
| Indian Pines | training time | 0.38 | 2.29 | 869.55 | — | 126.19 | 4.35 | 3786.11 | 1543.04 | 216.96 | 565.21 | 329.99 | 565.21 | 329.99 |
| testing time | 3.16 | 3.34 | 27.95 | 116.90 | 7.16 | 3.43 | 248.39 | 126.18 | 0.91 | 717.88 | 748.80 | 718.37 | 749.34 |
| Pavia University | training time | 0.74 | 8.49 | 833.13 | — | 482.50 | 4.98 | 3328.64 | 1972.61 | 1425.93 | 777.43 | 964.78 | 777.43 | 964.78 |
| testing time | 7.54 | 22.08 | 97.42 | 447.06 | 134.82 | 16.62 | 265.37 | 181.16 | 2.479 | 885.61 | 1466.14 | 888.17 | 1468.62 |
Table 8 displays the classification results of the SpectralFormer method and the trained model of the proposed methods. The models of TDSL-S and TDSLMV-S with
,
, TDSL-P and TDSLMV-P with
, are the models trained in the aforementioned comparison experiments on Indian Pines. The models of TDSL-S and TDSLMV-S with
, TDSL-P and TDSLMV-P with
,
, are the models trained in the aforementioned comparison experiments on Pavia University data. It is obvious that the trained model is efficient when applied to a new dataset. The results of the trained models are superior to the results of SpectralFormer. In particular, the OAs of models trained in the experiments on Pavia University are more than
. The results of models trained in the experiments on Pavia University are better than the results of models trained in the experiments on Indian Pines. It is because the Houston2013 and Pavia University are both gathered over the city, while Indian Pines just contains agriculture, forest, and natural perennial vegetation. The classification results of the TDSLMV model trained in the experiments on Indian Pines achieve
and
, which are enough for general applications.
Figure 14 shows the three-band false-color composite image, ground truth map, classification maps, and the corresponding error maps for the Houston2013 dataset.
Figure 14a shows that the dataset is complex and the labeled categories are scattered. The classification map of SpectralFormer has many misclassified pixels, and the classification maps of the trained models just have a few misclassified pixels. This demonstrates that the trained feature extractor models are efficient when applied to a complex dataset.