Can Satellite and Atmospheric Reanalysis Products Capture Compound Moist Heat Stress-Floods?
Abstract
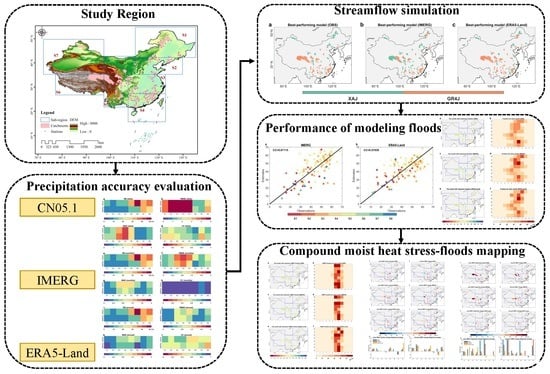
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.1.1. Meteorological Dataset
2.1.2. Observed Streamflow Data
2.2. Methods
2.2.1. Precipitation Indices for Evaluating Precipitation Estimation Accuracy
2.2.2. Hydrological Simulations
2.2.3. Identifying Compound Moist Heat-Flood Events
3. Results
3.1. Performance Assessments of IMERG and ERA5-Land Precipitation
3.2. Calibration and Validation of Hydrological Models
3.3. Performance of Modeling Extreme Streamflow
3.4. CMHF Mapping and Performance Assessment
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Soe, K.M.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Applications of TRMM- and GPM-Era Multiple-Satellite Precipitation Products for Flood Simulations at Sub-Daily Scales in a Sparsely Gauged Watershed in Myanmar. Remote Sens. 2019, 11, 140. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, B.; Ma, Z.; Chen, X.; Qiu, J.; Liu, D. Comprehensive Comparisons of State-Of-The-Art Gridded Precipitation Estimates for Hydrological Applications over Southern China. Remote Sens. 2020, 12, 3997. [Google Scholar] [CrossRef]
- Almagro, A.; Oliveira, P.T.S.; Brocca, L. Assessment of bottom-up satellite rainfall products on estimating river discharge and hydrologic signatures in Brazilian catchments. J. Hydrol. 2021, 603, 126897. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The tropical rainfall measuring mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Nesbitt, S.W.; Cifelli, R.; Rutledge, S.A. Storm Morphology and Rainfall Characteristics of TRMM Precipitation Features. Mon. Weather Rev. 2006, 134, 2702–2721. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Immerzeel, W.; Rutten, M.; Droogers, P. Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula. Remote Sens. Environ. 2009, 113, 362–370. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Teng, W.; Kempler, S. Tropical Rainfall Measuring Mission (TRMM) Precipitation Data and Services for Research and Applications. Bull. Am. Meteorol. Soc. 2012, 93, 1317–1325. [Google Scholar] [CrossRef] [Green Version]
- Pombo, S.; de Oliveira, R.P. Evaluation of extreme precipitation estimates from TRMM in Angola. J. Hydrol. 2015, 523, 663–679. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. Integrated Multi-satellitE Retrievals for GPM (IMERG) technical documenta-tion. Nasa/Gsfc Code 2019, 612, 2019. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J. Integrated multi-satellite retrievals for the Global Precipitation Measurement (GPM) mission (IMERG). In Satellite Precipitation Measurement; Springer: Cham, Germany, 2020; pp. 343–353. [Google Scholar]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Al-Falahi, A.H.; Saddique, N.; Spank, U.; Gebrechorkos, S.H.; Bernhofer, C. Evaluation the Performance of Several Gridded Precipitation Products over the Highland Region of Yemen for Water Resources Management. Remote Sens. 2020, 12, 2984. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Z.; Yan, S.; Peng, J. Do ERA5 and ERA5-land precipitation estimates outperform satellite-based precipitation products? A comprehensive comparison between state-of-the-art model-based and satellite-based precipitation products over mainland China. J. Hydrol. 2022, 605, 127353. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Jiang, L.; Madsen, H.; Bauer-Gottwein, P. Simultaneous calibration of multiple hydrodynamic model parameters using satellite altimetry observations of water surface elevation in the Songhua River. Remote Sens. Environ. 2019, 225, 229–247. [Google Scholar] [CrossRef]
- Xiong, W.; Tang, G.; Wang, T.; Ma, Z.; Wan, W. Evaluation of IMERG and ERA5 Precipitation-Phase Partitioning on the Global Scale. Water 2022, 14, 1122. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Smith, A.; Bates, P.D.; Wing, O.; Sampson, C.; Quinn, N.; Neal, J. New estimates of flood exposure in developing countries using high-resolution population data. Nat. Commun. 2019, 10, 1814. [Google Scholar] [CrossRef] [Green Version]
- Rentschler, J.; Salhab, M.; Jafino, B.A. Flood exposure and poverty in 188 countries. Nat. Commun. 2022, 13, 3527. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, B.; Rapuc, W.; Amann, B.; Anselmetti, F.S.; Arnaud, F.; Blanchet, J.; Brauer, A.; Czymzik, M.; Giguet-Covex, C.; Gilli, A.; et al. Impact of warmer climate periods on flood hazard in the European Alps. Nat. Geosci. 2022, 15, 118–123. [Google Scholar] [CrossRef]
- Wing, O.E.J.; Lehman, W.; Bates, P.D.; Sampson, C.C.; Quinn, N.; Smith, A.M.; Neal, J.C.; Porter, J.R.; Kousky, C. Inequitable patterns of US flood risk in the Anthropocene. Nat. Clim. Chang. 2022, 12, 156–162. [Google Scholar] [CrossRef]
- Cappucci, M. Storms Deluge New York City, Abruptly Ending Sweltering Heat Wave. The Washington Post, 23 July 2019. [Google Scholar]
- Zhang, W.; Villarini, G. Deadly Compound Heat Stress-Flooding Hazard Across the Central United States. Geophys. Res. Lett. 2020, 47, e2020GL089185. [Google Scholar] [CrossRef]
- Matthews, T.; Wilby, R.L.; Murphy, C. An emerging tropical cyclone–deadly heat compound hazard. Nat. Clim. Chang. 2019, 9, 602–606. [Google Scholar] [CrossRef]
- Wang, S.S.Y.; Kim, H.; Coumou, D.; Yoon, J.H.; Zhao, L.; Gillies, R.R. Consecutive extreme flooding and heat wave in Japan: Are they becoming a norm? Atmos. Sci. Lett. 2019, 20, e933. [Google Scholar] [CrossRef]
- Chen, Y.; Liao, Z.; Shi, Y.; Tian, Y.; Zhai, P. Detectable Increases in Sequential Flood-Heatwave Events Across China During 1961–2018. Geophys. Res. Lett. 2021, 48, e2021GL092549. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X.J. A gridded daily observation dataset over China region and comparison with the other datasets. Chin. J. Geophys. 2013, 56, 1102–1111. [Google Scholar] [CrossRef]
- Ning, G.; Luo, M.; Zhang, W.; Liu, Z.; Wang, S.; Gao, T. Rising risks of compound extreme heat-precipitation events in China. Int. J. Clim. 2022, 42, 5785–5795. [Google Scholar] [CrossRef]
- Yang, F.; Lu, H.; Yang, K.; He, J.; Wang, W.; Wright, J.S.; Li, C.; Han, M.; Li, Y. Evaluation of multiple forcing data sets for precipitation and shortwave radiation over major land areas of China. Hydrol. Earth Syst. Sci. 2017, 21, 5805–5821. [Google Scholar] [CrossRef] [Green Version]
- Nie, Y.; Sun, J. Evaluation of High-Resolution Precipitation Products over Southwest China. J. Hydrometeorol. 2020, 21, 2691–2712. [Google Scholar] [CrossRef]
- Shi, X.; Xu, X. Regional characteristics of the interdecadal turning of winter/summer climate modes in Chinese mainland. Chin. Sci. Bull. 2007, 52, 101–112. [Google Scholar] [CrossRef]
- Li, H.; Hong, Y.; Xie, P.; Gao, J.; Niu, Z.; Kirstetter, P.; Yong, B. Variational merged of hourly gauge-satellite precipitation in China: Preliminary results. J. Geophys. Res. Atmos. 2015, 120, 9897–9915. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q. Comparative analysis of CMIP3 and CMIP5 global climate models for simulating the daily mean, maximum, and minimum temperatures and daily precipitation over China. J. Geophys. Res. Atmos. 2015, 120, 4806–4824. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q. Changes in the Spatial Heterogeneity and Annual Distribution of Observed Precipitation across China. J. Clim. 2017, 30, 9399–9416. [Google Scholar] [CrossRef]
- Miao, C.; Duan, Q.; Sun, Q.; Lei, X.; Li, H. Non-uniform changes in different categories of precipitation intensity across China and the associated large-scale circulations. Environ. Res. Lett. 2019, 14, 025004. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Gu, L.; Zeng, Z.; Liu, D.; Chen, J.; Shen, Y.; Xu, C.-Y. Blending multi-satellite, atmospheric reanalysis and gauge precipitation products to facilitate hydrological modelling. J. Hydrol. 2021, 593, 125878. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Gentine, P.; Sullivan, S.C.; Gu, L.; He, S.; Chen, J.; Liu, P. Does the Hook Structure Constrain Future Flood Intensification Under Anthropogenic Climate Warming? Water Resour. Res. 2021, 57, e2020WR028491. [Google Scholar] [CrossRef]
- Ren-Jun, Z. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, J.; Elmahdi, A.; Li, X.; Liu, J.; Liu, Y.; Jin, J.; Liu, Y.; Bao, Z.; Liu, C.; et al. The Capacity of the Hydrological Modeling for Water Resource Assessment under the Changing Environment in Semi-Arid River Basins in China. Water 2019, 11, 1328. [Google Scholar] [CrossRef]
- Gu, L.; Chen, J.; Yin, J.; Xu, C.; Zhou, J. Responses of precipitation and runoff to climate warming and implications for future drought changes in China. Earth’s Futur. 2020, 8, e2020EF001718. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model?: Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Valéry, A.; Andréassian, V.; Perrin, C. ‘As simple as possible but not simpler’: What is useful in a temperature-based snow-accounting routine? Part 2—Sensitivity analysis of the Cemaneige snow accounting routine on 380 catchments. J. Hydrol. 2014, 517, 1176–1187. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Xu, C.; Zhang, J.; Chen, H. A Framework to Quantify the Uncertainty Contribution of GCMs Over Multiple Sources in Hydrological Impacts of Climate Change. Earth’s Futur. 2020, 8, e2020EF001602. [Google Scholar] [CrossRef]
- Arsenault, R.; Essou, G.R.C.; Brissette, F.P. Improving Hydrological Model Simulations with Combined Multi-Input and Multimodel Averaging Frameworks. J. Hydrol. Eng. 2017, 22, 04016066. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, J.; Zhang, X.J.; Xu, C.-Y.; Chen, H. Impacts of Using State-of-the-Art Multivariate Bias Correction Methods on Hydrological Modeling Over North America. Water Resour. Res. 2020, 56, e2019WR026659. [Google Scholar] [CrossRef]
- Gu, L.; Chen, J.; Yin, J.; Slater, L.J.; Wang, H.; Guo, Q.; Feng, M.; Qin, H.; Zhao, T. Global Increases in Compound Flood-Hot Extreme Hazards Under Climate Warming. Geophys. Res. Lett. 2022, 49, e2022GL097726. [Google Scholar] [CrossRef]
- Stull, R.B. Wet-Bulb Temperature from Relative Humidity and Air Temperature. J. Appl. Meteorol. Clim. 2011, 50, 2267–2269. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Chan, T.O.; Zhang, W.; Ning, G.; Wang, P.; Tong, X.; Xu, F.; Tian, H.; Han, Y.; Zhao, Y.; et al. Increasing Compound Heat and Precipitation Extremes Elevated by Urbanization in South China. Front. Earth Sci. 2021, 9, 636777. [Google Scholar] [CrossRef]
- Wang, H.-M.; Chen, J.; Cannon, A.J.; Xu, C.-Y.; Chen, H. Transferability of climate simulation uncertainty to hydrological impacts. Hydrol. Earth Syst. Sci. 2018, 22, 3739–3759. [Google Scholar] [CrossRef]
- Raymond, C.; Singh, D.; Horton, R.M. Spatiotemporal Patterns and Synoptics of Extreme Wet-Bulb Temperature in the Contiguous United States. J. Geophys. Res. Atmos. 2017, 122, 13108–13124. [Google Scholar] [CrossRef]
- Schwingshackl, C.; Sillmann, J.; Vicedo-Cabrera, A.M.; Sandstad, M.; Aunan, K. Heat Stress Indicators in CMIP6: Estimating Future Trends and Exceedances of Impact-Relevant Thresholds. Earth’s Future 2021, 9, e2020EF001885. [Google Scholar] [CrossRef]
- Guo, Q.; Zhou, X.; Satoh, Y.; Oki, T. Irrigated cropland expansion exacerbates the urban moist heat stress in northern India. Environ. Res. Lett. 2022, 17, 054013. [Google Scholar] [CrossRef]
- Gu, L.; Chen, J.; Yin, J.; Xu, C.-Y.; Chen, H. Drought hazard transferability from meteorological to hydrological propagation. J. Hydrol. 2020, 585, 124761. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Yang, Y.; Chen, J.; Gu, L.; Wang, J.; He, S.; Wu, B.; Xiong, J. Projection of droughts and their socioeconomic exposures based on terrestrial water storage anomaly over China. Sci. China Earth Sci. 2022, 65, 1772–1787. [Google Scholar] [CrossRef]
- You, J.; Wang, S. Higher Probability of Occurrence of Hotter and Shorter Heat Waves Followed by Heavy Rainfall. Geophys. Res. Lett. 2021, 48, e2021GL094831. [Google Scholar] [CrossRef]
- Yin, J.; Gentine, P.; Zhou, S.; Sullivan, S.C.; Wang, R.; Zhang, Y.; Guo, S. Large increase in global storm runoff extremes driven by climate and anthropogenic changes. Nat. Commun. 2018, 9, 4389. [Google Scholar] [CrossRef] [Green Version]













| ID | Index | Expression | Description | Perfect Score |
|---|---|---|---|---|
| 1 | MAE | mean absolute error | 0 | |
| 2 | CC | correlation coefficient | 1 | |
| 3 | POD | probability of detection | 1 | |
| 4 | FAR | false alarm ratio | 0 | |
| 5 | CSI | critical success index | 1 | |
| 6 | HSS | Heidke skill score | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, L.; Gu, Z.; Guo, Q.; Fang, W.; Zhang, Q.; Sun, H.; Yin, J.; Zhou, J. Can Satellite and Atmospheric Reanalysis Products Capture Compound Moist Heat Stress-Floods? Remote Sens. 2022, 14, 4611. https://doi.org/10.3390/rs14184611
Gu L, Gu Z, Guo Q, Fang W, Zhang Q, Sun H, Yin J, Zhou J. Can Satellite and Atmospheric Reanalysis Products Capture Compound Moist Heat Stress-Floods? Remote Sensing. 2022; 14(18):4611. https://doi.org/10.3390/rs14184611
Chicago/Turabian StyleGu, Lei, Ziye Gu, Qiang Guo, Wei Fang, Qianyi Zhang, Huaiwei Sun, Jiabo Yin, and Jianzhong Zhou. 2022. "Can Satellite and Atmospheric Reanalysis Products Capture Compound Moist Heat Stress-Floods?" Remote Sensing 14, no. 18: 4611. https://doi.org/10.3390/rs14184611
APA StyleGu, L., Gu, Z., Guo, Q., Fang, W., Zhang, Q., Sun, H., Yin, J., & Zhou, J. (2022). Can Satellite and Atmospheric Reanalysis Products Capture Compound Moist Heat Stress-Floods? Remote Sensing, 14(18), 4611. https://doi.org/10.3390/rs14184611