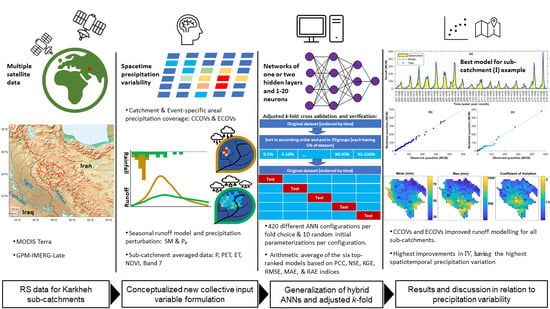
The methodology of the study combined satellite-based data introduced above [
32,
35,
45,
46,
48,
49,
50] to formulate new collective input variables for improved modelling of catchment runoff response to areal precipitation using Artificial Intelligence (AI)-assisted DD approaches. The ANNs [
14,
15,
43] and a
k-fold process [
51,
52,
53] with the adjustment described in the following Sections were used as reference for the evaluation. Both statistical and visual comparisons (introduced below) between modelled and observed discharge were performed. A particular aim of the present study was to improve simulation of monthly runoff from the five sub-catchments of the KRB in a mountainous environment. Such a study area characteristic largely demands for improved hydrological modelling according to the literature [
9,
10,
11]. The results of the study could increase added values of both satellite data and DD models for large-scale hydrological simulations and strategic surface water management at sparsely gauged locations. In conclusion, the novelty of the study lies in the new satellite-based input variable formulation for DD modelling of monthly runoff, and the hybrid scheme for generalization of the ANN model.
3.1. Modelling Architecture and Settings of ANN
Resembling human mind traits, i.e., learning for problem-solving, ANNs are a well-known type of AI models. ANNs are DD-machine learning systems that are widely used for non-linear function fitting problems in hydrology. The architecture of an ANN is based on a set of connected neurons spread over one or more hidden layers, for shallow to deep networks, between input and output layers [
14,
15,
18]. The input and output variables are vectors of equal size for time series of involved variables (precipitation, ET, etc.) and runoff, respectively. The simplest ANN model can be thought of as a single neuron in a hidden layer. This neuron multiplies each input vector
(
, where
is number of input variables) in the input layer with a scalar weight
, and adds sums of weighted inputs with a scalar bias
to allocate
to the neuron, where
and
are typically random values between −1 and 1. Next, an activation (or transfer) function
was applied to
, i.e.,
, to produce first estimation of the output variable (i.e., runoff) in the range of, e.g., 0 to 1, −1 to 1, or beyond if a log-sigmoid, a hyperbolic tangent sigmoid, or a linear transfer function is employed, respectively. Since input variables and runoff are usually normalized over −1 and 1 before use in the ANNs, estimated outputs must be returned to the previous scale to give actual runoff estimates.
For larger ANNs, each neuron in each layer treats outputs of all neurons in the previous layer as inputs and so forth. This one-way non-recurrent data progress for model development is known as feedforward. Thus, the output layer of an ANN with one output variable (runoff) is always a single neuron that transfers the previous hidden layer’s outputs to estimates of the output variable. Consequently, estimates of the runoff vector from a three-layer ANN can be written as [
54]:
where superscripts
denote layer number, and
and
are
and
matrices of the input variables (involving features) and weights, respectively. Additionally, b is a scalar value representing bias,
is estimated output vector of
length, and
is number of input–output data pairs, equivalent to the studied length of monthly runoff time series (i.e., 205). The transfer functions
may differ from one layer to another. They control the non-linearity of the modelling, and, without them, ANNs are nothing but a group of linear functions of input variables [
15]. Nevertheless, the functions should be differentiable with respect to parameters (i.e.,
and
) to be optimized using gradient- or Jacobian-based methods after some iterations. For the final output layer (here,
), the study used a linear function, i.e.,
, while, for the hidden layers (here,
and
), the hyperbolic tangent sigmoid transfer function was adopted expressed as [
54]:
Upon initialization with a random set of parameters (
and
), the ANN repeatedly adjusted them by determining direction and steps at each iteration to minimize the loss function as an equation of the model’s residual (i.e., difference between estimated and observed runoff) until a stopping rule was met, i.e., when the gradient was close to zero, the step size for parameterization was too small, or the number of iterations (epochs) exceeded a specified limit. This study applied a backpropagation learning algorithm based on the chain rule of the calculus as described in [
54] and the mean squared error performance criteria for the loss function [
54,
55]:
where,
and
are time series of observed and simulated runoff (
= 1, …,
).
A consequence of setting a too loose stop rule for ANN is overfitting during learning. Keeping a portion of the available data for validation is, therefore, necessary. An efficient, in-process way to skip overfitting is to set an early stopping rule for the learning process by checking model performance in each iteration for the validation portion of the data not used for parameterization. Thus, continuous reduction in the model performance for the kept-out, validation data by iteration for certain times (i.e., maximum number of validation fails) can be considered a signal of overfitting that stops the parameterization process. The modelling parameters were stored for each iteration, and the final model was fixed with parameterization based on the minimum value of loss function for validation.
Prior knowledge of architecture and settings for an ANN that best suits a hydrological problem is difficult to incorporate [
14]. Thus, in this study, networks with different configurations (
Table 2) were evaluated and ranked by their modelling scores based on six statistical criteria as introduced in
Table 3. The backpropagation training algorithm was the Levenberg–Marquardt (LM) algorithm that, in many cases, can obtain lower MSE than other algorithms according to the MATLAB recommendations.
As described in [
55], most of the goodness-of-fit indices in hydrology, e.g., Nash–Sutcliffe efficiency (NSE), and Kling–Gupta efficiency (KGE), are related to MSE (or RMSE =
), Pearson correlation coefficient (PCC), and the mean and standard deviation of observed (
and
) and estimated runoff (
and
). For example, as seen in the alternative equation for the NSE in
Table 3, it is a function of the normalized MSE by
(variance of runoff observations). While MSE varies between 0 and infinity (MSE = 0 as ideal fit), NSE ≤ 0 shows a non-interesting condition of the model, being equivalent to or worse than using the mean of the observations as a simple model [
55]. As another example, from the reformulation of NSE [
55] in the form of
(where
and
with perfect values of 1 and 0, respectively), it is easy to interpret why NSE frequently takes a smaller value in comparison to PCC. Similarly, this decomposition of NSE explains that the larger the bias in the mean and variance of the estimated values, the larger the difference between the NSE and PCC. It is, therefore, important to know the possible range, as well as the perfect/worst values of the performance criteria for evaluation of the results.
Table 3 includes this information for the statistics used in the study and cites some references for further details around them [
55,
56,
57,
58].
In
Table 2, a 0 neuron on L2 was the state when only one hidden layer was employed. Thus, all possible combinations based on one or two hidden layers with 1–20 neurons on each resulted in 420 (20 × 21) different configurations. Since an ANN initializes with a random set of weights and biases, it can end with different parameterization and runoff estimates under a specific network configuration. Therefore, a preferred model must be saved as a net file containing both the configuration and parameters for future applications. For a more reliable selection of the best model with a specific configuration, random initial parameterization was repeated 10 times per configuration. For the sake of generalization of the modelled runoff, the average of estimates, from a higher number of repeats, could be used. However, only single repeats with the best performance scores were chosen. Generalization is a useful process to avoid noisy outputs for large ANNs and small datasets.
Section 3.2 and
Section 3.3 below include descriptions of how it was addressed in the study.
3.2. Dataset Partitioning and Adjusted k-Fold Process for Hybrid Modelling
A more robust framework for model development using ANN can rely on further verification of the modelling performance using new datasets for testing (or verification), other than the ones used for training and in-process validation that both together are hereinafter referred to as calibration. Training data are only used for parameterization. Validation data are not used directly for parameterization but are presented to the calibration for early stopping to avoid overfitting. Usually, most of the data are used for training. This is crucial especially when the available data are not large enough and keeping any data out for validation and verification is at cost of less calibration. However, less validation and verification data cannot guarantee a robust model for future uses.
A process of runoff data organization into the calibration and testing partitions is known as
k-fold cross-validation (or cross-verification) [
51,
52,
53]; that is, to randomly shuffle data and then divide it into
k separate parts of equal size (folds), each used once for testing in
k times running of the model, while the rest
k − 1 folds are left for calibration. Therefore, it is more accurate to call this a
k-fold cross-verification and (
k – 1)-fold cross-validation or simply cross validation and verification. Then, the modelling performance is usually reported based on mean and variance of modelling scores (
Table 3) obtained from
k runs. The
k-fold is mainly of interest for short data as it is the case for many hydrologically data-scarce catchments. An alternative method that selects the data partitions continuously rather than individual sampling for calibration/testing is challenging when the length of data is short, and, perhaps, all or none of the extreme values are selected for testing depending on the appeared sequence of events. Common values for
k are 5 and 10, corresponding to 20% and 10% of data for each fold, respectively. A concern for using the
k-fold process for runoff data is to equally distribute the variance of data, especially regarding the extremes (e.g., data above the 95th percentile), which is important for training of the ANN with an in-process early stopping validation. However, in the random shuffling of data, the chance for equal spread of a few extreme runoff values into all folds is small. Therefore, this study used a completely random data partitioning in the form of an adjusted
k-fold process that ensured a fair distribution of data to the folds as shown in
Figure 3 and described below for the 5-fold condition:
The runoff data were sorted by magnitude in ascending order.
The sorted data were split into 20 groups, each encompassing 5% of the data.
An almost equal portion of data from the groups was then moved randomly to each fold, so that all data within the groups were distributed to all folds at the end. A total of 205 monthly data (from 22 August 2000 to 22 September 2017 equivalent to 01/06/1379–31/06/1396 in Solar Hijri calendar) was categorized into 20 groups of 10 or 11 members. Then, almost one-kth of the groups’ members was allocated to each fold.
After distributing the data to the folds using above steps, iterative partitioning started with taking the first fold for testing. Then, k – 1 different ways were possible for choice of another fold (2, 3, 4, or 5) for validation, and remaining k − 2 folds were eventually used for training, without a degree of freedom.
For each iteration of k, having a constant fold chosen for testing, modelling was calibrated k – 1 (for different variation/ways of training-validation combinations) multiplied by 420 (for different combinations of hidden layers and neurons) multiplied by 10 (for different random parameter initialization) times. While the parameterization of each of the (k − 1) × 420 × 10 models was based on a minimum MSE for validation, they were additionally ranked based on the six performance criteria for calibration. For generalization of the output, a hybrid of the six best-ranked ANN models in the form of an arithmetic average was considered as final model for iteration k.
The previous steps were continued k times so that, eventually, there were k hybrid models with different testing partitions to evaluate their outputs with the observed runoff. Selection of the best hybrid model was based on the comparison of their performances in both calibration and testing partitions of the runoff data.
3.3. Input Data Combinations for Conceptualized Data-Driven Modelling
Taking advantage of the spatially distributed RS data, seasonality in the observed monthly runoff and estimated monthly satellite precipitation data, and simple concepts affecting the rainfall–runoff process, different combinations, and organization of input variables were developed. The basic RS-based inputs were spatially averaged catchment-scale monthly GPM-IMERG-Late and MODIS-Terra data as introduced in
Section 2.3 and
Section 2.4. Thus, the following grid-based calculations were carried out first:
- –
For ET (and PET), weighted sum of four or five consecutive 8-day time series data corresponding to their overlapping days within each month;
- –
For NDVI and B7, weighted average of two consecutive monthly time series data corresponding to their overlapping days within each month;
- –
For precipitation, sum of 29, 30, or 31 consecutive daily time series data in each month (note: water years in Iran starts with month 7 in Solar Hijri calendar and comprise five 30-day, one 29-day, and six 31-day months, except for leap years, where the sixth month is 30 days).
Then, the average of the resulting data for all grids from the above steps gave catchment-scale monthly RS-based data synced to the available monthly runoff data.
As mentioned in the introduction, two new types of input variables were formulated based on the satellite precipitation data. In fact, the spatially averaged monthly catchment precipitation could be related to any situation ranging from an isolated local event to a more distributed event covering the catchment. To investigate the areal variability of precipitation in the form of additional features that can explain the catchment response variation, rather than using too many input variables equivalent to the number of grids within a catchment, the following procedure was utilized:
- –
First, the catchment-scale monthly precipitation (P) data were classified into 10 categories. For this purpose, they were sorted in an ascending order for each sub-catchment. The first category, with the smallest importance in producing runoff, was allocated to values between 0 and 2 mm/month, roughly encompassing 25% of the data depending on the sub-catchment. Remaining data (P > 2 mm/h) were first divided into eight additional categories with an almost equal data in each (roughly 9.4% of the data). In this way, however, the 9th category contained data with a wide range of values, including extremes. Thus, this category was further divided into two (roughly for percentiles 90–95 and 95–100) to avoid too long range of values in the 10th category.
- –
Then, a set of areal precipitation coverage values was calculated using the ratio of the catchment area that received precipitation within the range specified by each category. Thus, the number of catchment-specific precipitation coverage ratios (CCOVs) as input variables was equal to the number of precipitation categories with 11 denominators of P as below (rounded values are presented here):
- ■
Gamasiab (I): 0, 2, 8, 17, 24, 31, 38, 54, 82, 115, and 245;
- ■
Qarasu (II): 0, 2, 9, 24, 33, 42, 51, 74, 126, 169, and 410;
- ■
Seymareh (I–III): 0, 2, 9, 21, 31, 39, 52, 68, 108, 159, and 396;
- ■
Kashkan (IV): 0, 2, 9, 20, 32, 48, 63, 82, 118, 212, and 629;
- ■
Karkheh (I–V): 0, 2, 9, 23, 31, 43, 56, 73, 110, 157, and 410.
- –
Next, in addition to CCOVs, another set of data was obtained by calculating the ratio of the catchment area that received higher than 50, 75, 100, 125, 150, and 200% of the P for each month (hereinafter, ECOVs).
Accordingly, ECOVs are event-specific variables with varying precipitation ranges from one month to another, whereas CCOVs are based on fixed precipitation categories for a given catchment. The sum of CCOVs and ECOVs for each month was equal to 1. Thus:
where for each catchment of size
(=total number of GPM-IMERG grids, whose centres were located at the catchment’s border),
and
denote the number of grids that had a P in the
th category as introduced above for the CCOVs and ECOVs, respectively.
Finally, based on the seasonality of precipitation and runoff data, outputs of two simple calculations were also used as input variables. Nash and Barsi [
59] suggested that in catchments with seasonality/periodic signatures in runoff data, mean runoff can constitute a seasonal model. Further developments resulted in a linear perturbation model (LPM) as described in [
25], where, instead of using actual runoff and precipitation, perturbations (departures) from the seasonal estimates of precipitation and runoff could be modelled. The output of such a perturbation model can be added to the output from the seasonal model to provide a hybrid modelling of runoff. Same theories were later employed in DD modelling of precipitation–runoff and referred to as non-linear perturbation model (NLPM), e.g., [
40,
60]. Such input is feasible to reduce the system complexity and improve the model efficiency of ANN models [
60]. Accordingly:
- –
One variable was a simple estimator of runoff using seasonal mean/model (SM) [
59]:
where
y is runoff,
d and
r indicate date and year, respectively, and
R is total number of years. In the adjusted
k-fold process here,
Rd is total repeats of month
d in the calibration, and
D is the cycle period (i.e., 12 for monthly data).
- –
The other variable was precipitation perturbation (P
p) inspired from the notion of linear perturbation model [
59,
61]:
where PSM is a seasonal model of P calculated such as Equation (8) using P instead of
y.
A complete list of the input variable combinations is presented in
Table 4. Finally, all input variables (
Table 4) were introduced with 0–2-month lags (Lag 0–2) to evaluate possible patterns obtainable from the memory of the hydrological system. Then, the total length of the datasets used for modelling was two months smaller than the available common period of runoff and RS-based data. Regardless of the SM, combinations of the RS-based input variables in
Table 4 could be considered in three classes depending on the affecting factors employed according to:
- A.
Precipitation and potential ET (Comb. 1–4);
- B.
Precipitation, potential ET, and NDVI (Comb. 5–8);
- C.
Precipitation, potential ET, actual ET, NDVI, and B7 (Comb. 9–12).