A Refined Model for Quad-Polarimetric Reconstruction from Compact Polarimetric Data
Abstract
:1. Introduction
2. Related Basis
2.1. Quad-PolSAR and Freeman-Durden Decomposition
2.2. Compact-PolSAR and the Classical Reconstruction Approach
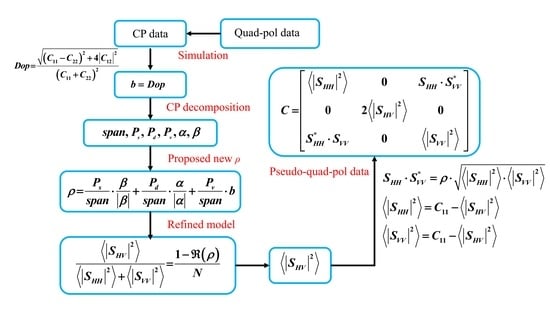
3. Proposed Reconstruction
3.1. CP Decomposition Method
3.2. Estimation of
3.3. Reconstruction Method
4. Experiments and Discussion
4.1. Experiment on San Francisco Data
4.1.1. Gaofen-3 Data
4.1.2. ALOS-2 Data
4.2. Experiment on Flevoland Data
4.2.1. Data Set and Reconstruction
4.2.2. Performance on CV-CNN Classifier
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Yu, H.; Lan, Y.; Gong, S.; Xing, M. CANet: An unsuperivised deep convolutional neural network for efficient cluster-anlysis-based multibaseline InSAR phase unwrapping. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Yiğit, E.; Demirci, Ş.; Özdemir, C. Clutter removal in millimeter wave GB-SAR images using OTSU’s thresholding method. Int. J. Eng. Geosci. 2022, 7, 43–48. [Google Scholar] [CrossRef]
- Demirci, Ş.; Özdemir, C. An investigation of the performances of polarimetric target decompositions using GB-SAR imaging. Int. J. Eng. Geosci. 2021, 6, 9–19. [Google Scholar] [CrossRef]
- Duysak, H.; Yiğit, E. Investigation of the performance of different wavelet-based fusions of SAR and optical images using Sentinel-1 and Sentinel-2 datasets. Int. J. Eng. Geosci. 2022, 7, 81–90. [Google Scholar] [CrossRef]
- Ohki, M.; Shimada, M. Large-area land use and land cover classification with quad, compact, and dual polarization SAR data by PALSAR-2. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5550–5557. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, M.; Zeng, J.; Wei, X.; Shi, H. Evaluation of Gaofen-3 C-Band SAR for soil moisture retrieval using different polarimetric decomposition models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5707–5719. [Google Scholar] [CrossRef]
- Chang, Y.; Anagaw, A.; Chang, L.; Wang, Y.; Hsiao, C.; Lee, W. Ship Detection Based on YOLOv2 for SAR imagery. Remote Sens. 2019, 11, 786. [Google Scholar] [CrossRef] [Green Version]
- Souyris, J.; Imbo, P.; Fjortoft, R.; Mingot, S.; Lee, J.-S. Compact polarimetry based on symmetry properties of geophysical media: The π/4 model. IEEE Trans. Geosci. Remote Sens. 2005, 43, 634–646. [Google Scholar] [CrossRef]
- Stacy, N.; Preiss, M. Compact polarimetric analysis of X-band SAR data. In Proceedings of the 6th European Conference on Synthetic Aperture Radar, Dresden, Germany, 16–18 May 2006. [Google Scholar]
- Raney, R.K. Hybrid-Polarity SAR architecture. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3397–3404. [Google Scholar] [CrossRef]
- Raney, R.K.; Cahill, J.T.; Patterson, C.W.; Bussey, D.B. The m-chi decomposition of hybrid dual-polarimetric radar data with application to lunar craters. J. Geophys. Res. Planets 2012, 117, E00H21. [Google Scholar] [CrossRef]
- Raney, R.K.; Spudis, P.D.; Bussey, D.B.; Crusan, J.; Jensen, J.R.; Marinelli, W. The lunar mini-RF radars: Hybrid polarimetric architecture and initial results. Proc. IEEE 2011, 99, 808–823. [Google Scholar] [CrossRef]
- Turkar, V.; De, S.; Rao, Y.S.; Shitole, S.; Bhattacharya, A.; Das, A. Comparative analysis of classification accuracy for RISAT-1 compact polarimetric data for various land-covers. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, IGARSS 2013, Melbourne, Australia, 21–26 July 2013. [Google Scholar]
- Rosenqvist, A.; Shimada, M.; Suzuki, S.; Ohgushi, F.; Tadono, T.; Watanaba, M. Operational performance of the ALOS global systematic acquisition strategy and observation plans for ALOS-2 PALSAR-2. Remote Sens. Environ. 2014, 155, 3–12. [Google Scholar] [CrossRef]
- Geldsetzer, T.; Khurshid, S.K.; Warner, K.; Botelho, F.; Flett, D. Wind speed retrieval from simulated RADARSAT Constellation Mission compact polarimetry SAR data for marine application. Remote Sens. 2019, 11, 1682. [Google Scholar] [CrossRef] [Green Version]
- Cloude, S.R.; Goodenough, D.G.; Chen, H. Compact decomposition theory. IEEE Geosci. Remote Sens. Lett. 2012, 9, 28–32. [Google Scholar] [CrossRef]
- Guo, R.; Liu, Y.-B.; Wu, Y.-H.; Zhang, S.-X.; Xing, M.-D.; He, W. Applying H/α decomposition to compact polarimetric SAR. IET Radar Sonar Navig. 2012, 6, 61–70. [Google Scholar] [CrossRef]
- Nord, M.; Ainsworth, T.; Lee, J.-S.; Stacy, N. Comparison of compact polarimetric synthetic aperture radar modes. IEEE Trans. Geosci. Remote Sens. 2009, 47, 174–188. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.-Z.; Chen, J.; Zhang, H.-S. Improved compact polarimetric SAR quad-pol reconstruction algorithm for oil spill detection. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1139–1142. [Google Scholar] [CrossRef]
- Collins, M.; Denbina, M.; Atteia, G. On the reconstruction of quad-pol SAR data from compact polarimetry data for ocean target detection. IEEE Trans. Geosci. Remote Sens. 2013, 51, 591–600. [Google Scholar] [CrossRef]
- Espeseth, M.; Brekke, C.; Anfinsen, S. Hybrid-Polarity and reconstruction methods for sea ice with L- and C-band SAR. IEEE Geosci. Remote Sens. Lett. 2016, 13, 467–471. [Google Scholar] [CrossRef]
- Kumar, A.; Panigrahi, R.K. Entropy based reconstruction technique for analysis of hybrid-polarimetric SAR data. IET Radar Sonar Navig. 2019, 13, 620–626. [Google Scholar] [CrossRef]
- Yang, J.; Yin, J.; Moon, W. Model-based pseudo-quad-pol reconstruction from compact polarimetry and its application to oil-spill observation. J. Sens. 2015, 2015, 734848. [Google Scholar]
- Yin, J.; Papathanassiou, K.; Yang, J.; Chen, P. Least-squares estimation for pseudo quad-pol image reconstruction from linear compact polarimetric SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3746–3758. [Google Scholar] [CrossRef]
- Yin, J.; Yang, J. Framework for Reconstruction of pseudo quad polarimetric imagery from general compact polarimetry. Remote Sens. 2021, 13, 530. [Google Scholar] [CrossRef]
- Yue, D.-X.; Xu, F.; Jin, Y.-Q. Wishart–Bayesian reconstruction of quad-pol from compact-pol SAR image. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1623–1627. [Google Scholar] [CrossRef]
- Gu, F.; Zhang, H.; Wang, C. Quad-pol reconstruction from compact polarimetry using a fully convolutional network. Remote Sens. Lett. 2020, 11, 397–406. [Google Scholar] [CrossRef]
- Zhang, F.; Cao, Z.; Xiang, D.; Hu, C.; Ma, F.; Yin, Q.; Zhou, Y.S. Pseudo quad-pol simulation from compact polarimetric SAR data via a complex-valued dual-branch convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 15, 901–918. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S. A three-component scattering model for polarimetric SAR data. IEEE Trans Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef] [Green Version]
- Van Zyl, J. Unsupervised classification of scattering behavior using radar polarimetry data. IEEE Trans. Geosci. Remote Sens. 1989, 27, 36–45. [Google Scholar] [CrossRef]
- Freeman, A. Fitting a two-component scattering model to polarimetric SAR data from forests. IEEE Trans. Geosci. Remote Sen. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Hajnsek, I.; Jagdhuber, T.; Schon, H.; Papathanassiou, K.P. Potential of estimating soil moisture under vegetation cover by means of PolSAR. IEEE Trans Geosci. Remote Sens. 2009, 47, 442–454. [Google Scholar] [CrossRef]
- Hong, W. Hybrid-polarity architecture based polarimetric SAR: Principles and applications. J. Radars 2016, 5, 559–595. [Google Scholar]
- Guo, R.; He, W.; Zhang, S.-X.; Zang, B.; Xing, M.-D. Analysis of three-component decomposition to compact polarimetric synthetic aperture radar. IET Radar Sonar Navig. 2014, 8, 685–691. [Google Scholar] [CrossRef]
- Xu, F.; Wang, H.-P.; Jin, Y.-Q. Deep learning as applied in SAR target recognition and terrain classification. J. Radars 2017, 6, 136–148. [Google Scholar]
- Acaer, H.; Özerdem, M.S.; Acar, E. Soil moisture inversion via semiempirical and machine learning methods with full-polarization Radarsat-2 and polarimetric target decomposition data: A comparative study. IEEE Access 2020, 8, 97896–197907. [Google Scholar]













| Mean Error | Ocean Area | Mountain Area | Urban Area | Total |
|---|---|---|---|---|
| Real part | 0.0037 | 0.1315 | 0.1518 | 0.0701 |
| Imaginary part | 0.0126 | 0.0939 | 0.0952 | 0.0631 |
| Model | Time Costs | Metrics | ||||
|---|---|---|---|---|---|---|
| Souyris’ model | 2700 s | Mean | 0.0729 | 2.2379 | 0.0970 | 0.0853 |
| Std. | 0.1387 | 2.6883 | 0.1610 | 0.1272 | ||
| CE | 5.122 × 10−5 | 0.2222 | 0.0014 | 0.1588 | ||
| Nord’s model | 2718 s | Mean | 0.0704 | 1.6177 | 0.0907 | 0.0634 |
| Std. | 0.1451 | 2.2744 | 0.1597 | 0.0928 | ||
| CE | 2.912 × 10−5 | 0.1252 | 8.021 × 10−5 | 0.0542 | ||
| Espeseth’s model | - | Mean | 0.0856 | 2.4160 | 0.1077 | - |
| Std. | 0.1518 | 2.6191 | 0.1603 | - | ||
| CE | 0.0015 | 0.0794 | 0.0026 | - | ||
| Kumar’ model | - | Mean | 0.0689 | 3.2072 | 0.0809 | - |
| Std. | 0.1471 | 3.2833 | 0.1510 | - | ||
| CE | 2.699 × 10−5 | 0.2045 | 4.518 × 10−5 | - | ||
| Proposed model | 2236 s | Mean | 0.0676 | 0.6805 | 0.0753 | 0.0638 |
| Std. | 0.1518 | 1.0342 | 0.1509 | 0.1099 | ||
| CE | 3.201 × 10−5 | 0.0439 | 4.106 × 10−5 | 0.0191 |
| Model | Time Costs | Metrics | ||||
|---|---|---|---|---|---|---|
| Souyris’ model | 7897 s | Mean | 0.1243 | 2.1401 | 0.1397 | 0.1433 |
| Std. | 0.1268 | 3.7699 | 0.1565 | 0.1179 | ||
| CE | 0.0196 | 0.6546 | 0.0152 | 0.2680 | ||
| Nord’s model | 8177 s | Mean | 0.1138 | 1.7158 | 0.1250 | 0.1158 |
| Std. | 0.1330 | 2.7809 | 0.1519 | 0.1022 | ||
| CE | 0.0156 | 0.4840 | 0.0111 | 0.1729 | ||
| Espeseth’s model | - | Mean | 0.1566 | 2.3299 | 0.1567 | - |
| Std. | 0.1461 | 2.8385 | 0.1657 | - | ||
| CE | 0.0374 | 0.3237 | 0.0235 | - | ||
| Kumar’s model | - | Mean | 0.0900 | 1.0940 | 0.0889 | - |
| Std. | 0.1335 | 1.7963 | 0.1350 | - | ||
| CE | 0.0077 | 0.3938 | 0.0025 | - | ||
| Proposed model | 6050 s | Mean | 0.0789 | 0.5551 | 0.0824 | 0.0828 |
| Std. | 0.1329 | 1.0260 | 0.1348 | 0.0978 | ||
| CE | 0.0013 | 0.0638 | 0.0013 | 0.0483 |
| Quad-Pol | CP | Souyris | Nord | Proposed | |
|---|---|---|---|---|---|
| Steam bean | 99.91 | 99.05 | 99.57 | 99.31 | 99.74 |
| Forest | 99.01 | 99.34 | 98.96 | 99.07 | 98.46 |
| Wheat | 98.55 | 96.65 | 98.35 | 97.40 | 97.45 |
| Potatoes | 99.26 | 99.00 | 99.37 | 99.21 | 99.32 |
| Grasses | 97.45 | 96.50 | 96.70 | 93.55 | 97.05 |
| Barley | 99.58 | 98.03 | 98.51 | 99.17 | 99.58 |
| Wheat 3 | 97.85 | 97.65 | 97.50 | 97.90 | 98.55 |
| Peas | 98.82 | 94.45 | 92.94 | 95.63 | 98.81 |
| Lucerne | 95.25 | 92.73 | 94.96 | 91.14 | 90.20 |
| Beet | 94.95 | 85.70 | 85.50 | 89.45 | 88.80 |
| Bare soil | 98.01 | 94.06 | 94.71 | 97.49 | 97.49 |
| Rapeseed | 96.65 | 91.30 | 90.80 | 86.30 | 90.85 |
| Wheat 2 | 99.00 | 98.00 | 98.75 | 97.05 | 98.85 |
| Water | 99.85 | 99.35 | 99.80 | 99.70 | 99.80 |
| Total | 98.15 | 95.84 | 96.17 | 95.88 | 96.78 |
| Model Features | Model Performance | |
|---|---|---|
| Souyris’ model | First proposed the relationship between and . | Performs well in the vegetation area, but not in other areas. |
| Nord’s model | Corrects the value of parameter N. | Performs slightly better than Souyris’ model in most regions. |
| Espeseth’s model | Estimates from Stokes vector. | Performs slightly worse than Souyris’ model. |
| Kumar’s model | Estimates from polarization entropy. | Performs better than Souyris’ model on L-band ALOS2 data, but worse on C-band Gaofen-3 data |
| Proposed model | Estimates through refined three-component decomposition, modifies the relationship between and . | Performs better than the other models. Reduces the reconstruction error and improves the model accuracy. Saves time compared to pixel-by-pixel models. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, R.; Zhao, X.; Zang, B.; Liang, Y.; Bai, J.; Guo, L. A Refined Model for Quad-Polarimetric Reconstruction from Compact Polarimetric Data. Remote Sens. 2022, 14, 5226. https://doi.org/10.3390/rs14205226
Guo R, Zhao X, Zang B, Liang Y, Bai J, Guo L. A Refined Model for Quad-Polarimetric Reconstruction from Compact Polarimetric Data. Remote Sensing. 2022; 14(20):5226. https://doi.org/10.3390/rs14205226
Chicago/Turabian StyleGuo, Rui, Xiaopeng Zhao, Bo Zang, Yi Liang, Jian Bai, and Liang Guo. 2022. "A Refined Model for Quad-Polarimetric Reconstruction from Compact Polarimetric Data" Remote Sensing 14, no. 20: 5226. https://doi.org/10.3390/rs14205226
APA StyleGuo, R., Zhao, X., Zang, B., Liang, Y., Bai, J., & Guo, L. (2022). A Refined Model for Quad-Polarimetric Reconstruction from Compact Polarimetric Data. Remote Sensing, 14(20), 5226. https://doi.org/10.3390/rs14205226