Msplit Estimation Approach to Modeling Vertical Terrain Displacement from TLS Data Disturbed by Outliers
Abstract
:1. Introduction
2. Functional Models and Methods
3. Simulated Data and Empirical Analysis
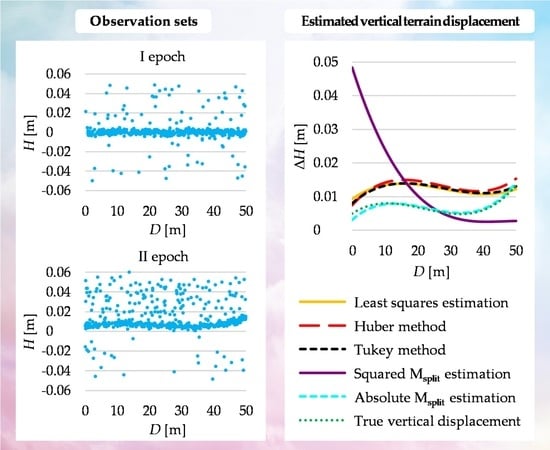
- Variant I—no outliers in any epoch;
- Variant II—10% positive outliers in epoch I, 10% positive outliers in epoch II;
- Variant III—10% positive outliers in epoch I, 30% positive outliers in epoch II;
- Variant IV—5% negative outliers in epoch I, 5% negative outliers in epoch II;
- Variant V—10% positive and 5% negative outliers in epoch I, 10% positive and 5% negative outliers in epoch II;
- Variant VI—10% positive and 5% negative outliers in epoch I, 30% positive and 5% negative outliers in epoch II.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gordon, S.J.; Lichti, D.D. Modeling Terrestrial Laser Scanner Data for Precise Structural Deformation Measurement. J. Surv. Eng. 2007, 133, 72–80. [Google Scholar] [CrossRef]
- Wang, C.; Hsu, P.-H. Building Detection and Structure Line Extraction from Airborne LiDAR Data. J. Photogramm. Remote Sens. 2007, 12, 365–379. [Google Scholar]
- Spaete, L.P.; Glenn, N.F.; Derryberry, D.R.; Sankey, T.T.; Mitchell, J.J.; Hardegree, S.P. Vegetation and Slope Effects on Accuracy of a LiDAR-Derived DEM in the Sagebrush Steppe. Remote Sens. Lett. 2011, 2, 317–326. [Google Scholar] [CrossRef]
- Rodríguez-Gonzálvez, P.; Jiménez Fernández-Palacios, B.; Muñoz-Nieto, Á.L.; Arias-Sanchez, P.; Gonzalez-Aguilera, D. Mobile LiDAR System: New Possibilities for the Documentation and Dissemination of Large Cultural Heritage Sites. Remote Sens. 2017, 9, 189. [Google Scholar] [CrossRef] [Green Version]
- Crespo-Peremarch, P.; Tompalski, P.; Coops, N.C.; Ruiz, L.Á. Characterizing Understory Vegetation in Mediterranean Forests Using Full-Waveform Airborne Laser Scanning Data. Remote Sens. Environ. 2018, 217, 400–413. [Google Scholar] [CrossRef]
- Matwij, W.; Gruszczyński, W.; Puniach, E.; Ćwiąkała, P. Determination of Underground Mining-Induced Displacement Field Using Multi-Temporal TLS Point Cloud Registration. Measurement 2021, 180, 109482. [Google Scholar] [CrossRef]
- Haddad, D.E.; Akçiz, S.O.; Arrowsmith, J.R.; Rhodes, D.D.; Oldow, J.S.; Zielke, O.; Toké, N.A.; Haddad, A.G.; Mauer, J.; Shilpakar, P. Applications of Airborne and Terrestrial Laser Scanning to Paleoseismology. Geosphere 2012, 8, 771–786. [Google Scholar] [CrossRef] [Green Version]
- Walicka, A.; Pfeifer, N. Automatic Segmentation of Individual Grains from a Terrestrial Laser Scanning Point Cloud of a Mountain River Bed. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1389–1410. [Google Scholar] [CrossRef]
- Mücke, W.; Deák, B.; Schroiff, A.; Hollaus, M.; Pfeifer, N. Detection of Fallen Trees in Forested Areas Using Small Footprint Airborne Laser Scanning Data. Can. J. Remote Sens. 2013, 39, S32–S40. [Google Scholar] [CrossRef]
- Kuzia, K. Application of airborne laser scanning in monitoring of land subsidence caused by underground mining expoloitation. Geoinform. Pol. 2016, 2016, 7–13. [Google Scholar] [CrossRef]
- Matkan, A.A.; Hajeb, M.; Mirbagheri, B.; Sadeghian, S.; Ahmadi, M. Spatial Analysis for Outlier Removal from LiDAR Data. In Proceedings of the The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Tehran, Iran, 15–17 November 2014; Copernicus GmbH: Göttingen, Germany, 2014; Volume XL-2-W3, pp. 187–190. [Google Scholar]
- Carrilho, A.C.; Galo, M.; Santos, R.C. Statistical Outlier Detection Method for Airborne LiDAR Data. In Proceedings of the ISPRS TC I Mid-term Symposium “Innovative Sensing—From Sensors to Methods and Applications”, Karlsruhe, Germany, 10–12 October 2018; Volume XLII–1, pp. 87–92. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, S.-C.; Whitman, D.; Shyu, M.-L.; Yan, J.; Zhang, C. A Progressive Morphological Filter for Removing Nonground Measurements from Airborne LIDAR Data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Gao, B.; Devereux, B. State-of-the-Art: DTM Generation Using Airborne LIDAR Data. Sensors 2017, 17, 150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Błaszczak-Bąk, W.; Janowski, A.; Kamiński, W.; Rapiński, J. Application of the Msplit Method for Filtering Airborne Laser Scanning Data-Sets to Estimate Digital Terrain Models. Int. J. Remote Sens. 2015, 36, 2421–2437. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. Determination of Terrain Models in Wooded Areas with Airborne Laser Scanner Data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for Point-Cloud Shape Detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Tóvári, D.; Pfeifer, N. Segmentation Based Robust Interpolation—A New Approach to Laser Data Filtering. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 36, 79–84. [Google Scholar]
- Nguyen, A.; Le, B. 3D Point Cloud Segmentation: A Survey. In Proceedings of the 2013 6th IEEE Conference on Robotics, Automation and Mechatronics (RAM), Manila, Philippines, 12–15 November 2013; pp. 225–230. [Google Scholar]
- Nurunnabi, A.; Belton, D.; West, G. Robust Statistical Approaches for Local Planar Surface Fitting in 3D Laser Scanning Data. ISPRS J. Photogramm. Remote Sens. 2014, 96, 106–122. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Yang, F.; Zhu, H.; Li, D.; Li, Y.; Tang, L. An Improved RANSAC for 3D Point Cloud Plane Segmentation Based on Normal Distribution Transformation Cells. Remote Sens. 2017, 9, 433. [Google Scholar] [CrossRef] [Green Version]
- Zhao, R.; Pang, M.; Liu, C.; Zhang, Y. Robust Normal Estimation for 3D LiDAR Point Clouds in Urban Environments. Sensors 2019, 19, 1248. [Google Scholar] [CrossRef] [Green Version]
- Berber, M.; Hekimoglu, S. What Is the Reliability of Conventional Outlier Detection and Robust Estimation in Trilateration Networks? Surv. Rev. 2003, 37, 308–318. [Google Scholar] [CrossRef]
- Lehmann, R.; Scheffler, T. Monte Carlo-Based Data Snooping with Application to a Geodetic Network. J. Appl. Geod. 2011, 5, 123–134. [Google Scholar] [CrossRef]
- Rofatto, V.F.; Matsuoka, M.T.; Klein, I.; Roberto Veronez, M.; da Silveira, L.G. A Monte Carlo-Based Outlier Diagnosis Method for Sensitivity Analysis. Remote Sens. 2020, 12, 860. [Google Scholar] [CrossRef] [Green Version]
- Hodges, J.L.; Lehmann, E.L. Estimates of Location Based on Rank Tests. Ann. Math. Statist. 1963, 34, 598–611. [Google Scholar] [CrossRef]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009; ISBN 978-0-470-43469-7. [Google Scholar]
- Baarda, W. A Testing Procedure for Use in Geodetic Networks; Publications on Geodesy 9; Rijkscommissie voor Geodesie: Delft, The Netherlands, 1968; Volume 2, ISBN 978 90 6132 209. [Google Scholar]
- Pope, A.J. The Statistics of Residuals and the Outlier Detection of Outliers; NOAA Technical Report; National Geodetic Survey: Rockville, MD, USA, 1976; Volume NGS 1.
- Gui, Q.; Zhang, J. Robust Biased Estimation and Its Applications in Geodetic Adjustments. J. Geod. 1998, 72, 430–435. [Google Scholar] [CrossRef]
- Duchnowski, R. Hodges-Lehmann Estimates in Deformation Analyses. J. Geod. 2013, 87, 873–884. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Yuan, Y.; Jia, N. More Efficient Methods among Commonly Used Robust Estimation Methods for GPS Coordinate Transformation. Surv. Rev. 2013, 45, 229–234. [Google Scholar] [CrossRef]
- Lehmann, R. On the Formulation of the Alternative Hypothesis for Geodetic Outlier Detection. J. Geod. 2013, 87, 373–386. [Google Scholar] [CrossRef] [Green Version]
- Wiśniewski, Z. Estimation of Parameters in a Split Functional Model of Geodetic Observations (Msplit Estimation). J. Geod. 2009, 83, 105–120. [Google Scholar] [CrossRef]
- Wiśniewski, Z. Msplit(q) Estimation: Estimation of Parameters in a Multi Split Functional Model of Geodetic Observations. J. Geod. 2010, 84, 355–372. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R.; Dumalski, A. Determination of Terrain Profile from TLS Data by Applying Msplit Estimation. Remote Sens. 2021, 13, 31. [Google Scholar] [CrossRef]
- Janowski, A.; Rapiński, J. M-Split Estimation in Laser Scanning Data Modeling. J. Indian Soc. Remote Sens. 2013, 41, 15–19. [Google Scholar] [CrossRef]
- Janowski, A. The Circle Object Detection with the Use of Msplit Estimation. E3S Web Conf. 2018, 26, 00014. [Google Scholar] [CrossRef] [Green Version]
- Janicka, J.; Rapiński, J.; Błaszczak-Bąk, W.; Suchocki, C. Application of the Msplit Estimation Method in the Detection and Dimensioning of the Displacement of Adjacent Planes. Remote Sens. 2020, 12, 3203. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R. Processing TLS Heterogeneous Data by Applying Robust Msplit Estimation. Measurement 2022, 197, 111298. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R. Msplit Estimation Based on L1 Norm Condition. J. Surv. Eng. 2019, 145, 04019006. [Google Scholar] [CrossRef]
- Kargoll, B. Comparison of Some Robust Parameter Estimation Techniques for Outlier Analysis Applied to Simulated GOCE Mission Data. In Proceedings of the Gravity, Geoid and Space Missions; Jekeli, C., Bastos, L., Fernandes, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 77–82. [Google Scholar]
- Chang, X.-W.; Guo, Y. Huber’s M-Estimation in Relative GPS Positioning: Computational Aspects. J. Geod. 2005, 79, 351–362. [Google Scholar] [CrossRef] [Green Version]
- Labant, S.; Weiss, G.; Kukučka, P. Robust Adjustment of a Geodetic Network Measured by Satellite Technology in the Dargovských Hrdinov Suburb. Acta Montan. Slovaca 2014, 16, 229–237. [Google Scholar]
- Yang, Y. Robust Estimation for Dependent Observations. Manuscr. Geod. 1994, 19, 10–17. [Google Scholar]
- Wiśniewski, Z. Total Msplit Estimation. J. Geod. 2022, 96, 82. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R. Iterative Process of Msplit(q) Estimation. J. Surv. Eng. 2020, 146, 06020002. [Google Scholar] [CrossRef]
- Forlani, G.; Nardinocchi, C. Adaptive Filtering of Aerial Laser Scanning Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 36, 130–135. [Google Scholar]
- Costantino, D.; Angelini, M.G. Production of DTM Quality by TLS Data. Eur. J. Remote Sens. 2013, 46, 80–103. [Google Scholar] [CrossRef] [Green Version]
- Cabaleiro, M.; Riveiro, B.; Arias, P.; Caamaño, J.C. Algorithm for Beam Deformation Modeling from LiDAR Data. Measurement 2015, 76, 20–31. [Google Scholar] [CrossRef]
- Nowel, K. Squared Msplit(q) S-Transformation of Control Network Deformations. J. Geod. 2019, 93, 1025–1044. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Z.; He, H.; Zhang, G.; Feng, Q.; Yang, H. A Squared Msplit Similarity Transformation Method for Stable Points Selection of Deformation Monitoring Network. Acta Geod. Cartogr. Sin. 2020, 49, 1419–1429. [Google Scholar] [CrossRef]
- Zienkiewicz, M.H. Determination of Vertical Indicators of Ground Deformation in the Old and Main City of Gdansk Area by Applying Unconventional Method of Robust Estimation. Acta Geodyn. Geomater. 2015, 12, 249–257. [Google Scholar] [CrossRef] [Green Version]
- Zienkiewicz, M.H. Deformation Analysis of Geodetic Networks by Applying Msplit Estimation with Conditions Binding the Competitive Parameters. J. Surv. Eng. 2019, 145, 04019001. [Google Scholar] [CrossRef]
- Lian, X.; Hu, H. Terrestrial Laser Scanning Monitoring and Spatial Analysis of Ground Disaster in Gaoyang Coal Mine in Shanxi, China: A Technical Note. Environ. Earth Sci 2017, 76, 287. [Google Scholar] [CrossRef]
- Zienkiewicz, M.H.; Hejbudzka, K.; Dumalski, A. Multi Split Functional Model of Geodetic Observations in Deformation Analyses of the Olsztyn Castle. Acta Geodyn. Geomater. 2017, 14, 195–204. [Google Scholar] [CrossRef]




| Variant | LS | Huber | Tukey | SMS | AMS |
|---|---|---|---|---|---|
| I | 0.29 | 0.33 | 0.30 | 0.50 | 0.43 |
| II | 0.38 | 0.20 | 0.13 | 0.25 | 0.15 |
| III | 5.62 | 5.63 | 5.68 | 10.13 | 0.16 |
| IV | 1.21 | 0.30 | 0.76 | 18.35 | 0.26 |
| V | 1.24 | 0.23 | 1.07 | 6.54 | 0.11 |
| VI | 5.48 | 6.27 | 5.51 | 14.73 | 0.62 |
| Variant | SMS | AMS |
|---|---|---|
| I | 15.17 | 10.88 |
| II | 26.32 | 1.82 |
| III | 28.87 | 21.18 |
| IV | 27.30 | 0.83 |
| V | 24.06 | 10.97 |
| VI | 25.47 | 17.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duchnowski, R.; Wyszkowska, P. Msplit Estimation Approach to Modeling Vertical Terrain Displacement from TLS Data Disturbed by Outliers. Remote Sens. 2022, 14, 5620. https://doi.org/10.3390/rs14215620
Duchnowski R, Wyszkowska P. Msplit Estimation Approach to Modeling Vertical Terrain Displacement from TLS Data Disturbed by Outliers. Remote Sensing. 2022; 14(21):5620. https://doi.org/10.3390/rs14215620
Chicago/Turabian StyleDuchnowski, Robert, and Patrycja Wyszkowska. 2022. "Msplit Estimation Approach to Modeling Vertical Terrain Displacement from TLS Data Disturbed by Outliers" Remote Sensing 14, no. 21: 5620. https://doi.org/10.3390/rs14215620
APA StyleDuchnowski, R., & Wyszkowska, P. (2022). Msplit Estimation Approach to Modeling Vertical Terrain Displacement from TLS Data Disturbed by Outliers. Remote Sensing, 14(21), 5620. https://doi.org/10.3390/rs14215620