Critical Climate Periods Explain a Large Fraction of the Observed Variability in Vegetation State
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Remote-Sensing-Based NDVI and LAI Datasets
2.3. Meteorological and Environmental Datasets
2.4. Ecosystem Category and Land Cover Datasets
2.5. Statistical Analysis of the Remote Sensing-Based Products
2.6. Critical Climate Period Analysis
2.7. Model Construction
3. Results
3.1. Multiannual Mean (MAM) and Interannual Variability (IAV) Curves
3.2. Relationships between the NDVI/LAI and the Climate Variables
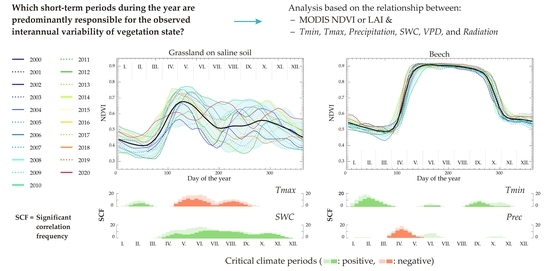
3.3. Critical Climate Periods
3.4. Relative Effects of the Climate Variables on Each Dominant Ecosystem
3.5. Important Climatic Variables during the Selected Period of the Year
3.6. Modeling NDVI and LAI in the Selected Late Summer Period
4. Discussion
4.1. Methodological Aspects
4.2. Moving-Window Correlation Analysis and Critical Climate Periods
4.3. Modeling
4.4. Uncertainty Issues: The Importance of the Land Cover Dataset
4.5. Uncertainty Issues: Trends
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderegg, W.R.L.; Hicke, J.A.; Fisher, R.A.; Allen, C.D.; Aukema, J.; Bentz, B.; Hood, S.; Lichstein, J.W.; Macalady, A.K.; McDowell, N.; et al. Tree mortality from drought, insects, and their interactions in a changing climate. New Phytol. 2015, 208, 674–683. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Xia, J.; Wang, Y.; Ahlström, A.; Chen, J.; Cook, R.B.; Cui, E.; Fang, Y.; Fisher, J.B.; Huntzinger, D.N.; et al. Enhanced peak growth of global vegetation and its key mechanisms. Nat. Ecol. 2018, 2, 1897–1905. [Google Scholar] [CrossRef] [PubMed]
- Catorci, A.; Lulli, R.; Malatesta, L.; Tavoloni, M.; Tardella, F.M. How the interplay between management and interannual climatic variability influences the NDVI variation in a sub-Mediterranean pastoral system: Insight into sustainable grassland use under climate change. Agric. Ecosyst. Environ. 2021, 314, 107372. [Google Scholar] [CrossRef]
- Piao, S.; Wang, X.H.; Park, T.; Chen, C.; Lian, X.; He, Y.; Bjerke, J.W.; Chen, A.; Ciais, P.; Tommervik, H.; et al. Characteristics, drivers and feedback of global greening. Nat. Rev. Earth Environ. 2020, 1, 14–27. [Google Scholar] [CrossRef] [Green Version]
- IPCC. Climate Change 2022: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Pörtner, H.-O., Roberts, D.C., Tignor, M., Poloczanska, E.S., Mintenbeck, K., Alegría, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., et al., Eds.; Cambridge University Press: Cambridge, UK, 2022; p. 3056. Available online: https://www.ipcc.ch/report/sixth-assessment-report-working-group-ii/ (accessed on 20 August 2022).
- Linscheid, N.; Estupinan-Suarez, L.M.; Brenning, A.; Carvalhais, N.; Cremer, F.; Gans, F.; Rammig, A.; Reichstein, M.; Sierra, C.A.; Mahecha, M.D. Towards a global understanding of vegetation–climate dynamics at multiple timescales. Biogeosciences 2020, 17, 945–962. [Google Scholar] [CrossRef]
- Seyednasrollah, B.; Young, A.M.; Li, X.; Milliman, T.; Ault, T.; Frolking, S.; Friedl, M.; Richardson, A.D. Sensitivity of deciduous forest phenology to environmental drivers: Implications for climate change impacts across North America. Geophys. Res. Lett. 2020, 47, e2019GL086788. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W. Drought-Induced Reduction in Global Terrestrial Net Primary Production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [Green Version]
- Zscheischler, J.; Mahecha, M.D.; von Buttlar, J.; Harmeling, S.; Jung, M.; Rammig, A.; Randerson, J.T.; Schölkopf, B.; Seneviratne, S.I.; Tomelleri, E. A few extreme events dominate global interannual variability in gross primary production. Environ. Res. Lett. 2014, 9, 035001. [Google Scholar] [CrossRef] [Green Version]
- Piao, S.; Liu, Q.; Chen, A.; Janssens, I.A.; Fu, Y.; Dai, J.; Liu, L.; Lian, X.; Shen, M.; Zhu, X. Plant phenology and global climate change: Current progresses and challenges. Glob. Change Biol. 2019, 25, 1922–1940. [Google Scholar] [CrossRef]
- Guo, L.; Cheng, J.; Luedeling, E.; Koerner, S.E.; He, J.S.; Xu, J.; Gang, C.; Li, W.; Luo, R.; Peng, C. Critical climate periods for grassland productivity on China’s Loess Plateau. Agric. For. Meteorol. 2017, 233, 101–109. [Google Scholar] [CrossRef]
- Chen, C.; He, B.; Guo, L.; Zhang, Y.; Xie, X.; Chen, Z. Identifying critical climate periods for vegetation growth in the northern hemisphere. J. Geophys. Res. Biogeosci. 2018, 123, 2541–2552. [Google Scholar] [CrossRef]
- Kern, A.; Barcza, Z.; Marjanovic, Z.; Árendás, T.; Fodor, N.; Bónis, P.; Bognár, P.; Lichtenberger, J. Statistical modelling of crop yield in Central Europe using climate data and remote sensing vegetation indices. Agric. For. Meteorol. 2018, 260–261, 300–320. [Google Scholar] [CrossRef]
- Vogel, J.; Rivoire, P.; Deidda, C.; Rahimi, L.; Sauter, C.A.; Tschumi, E.; van der Wiel, K.; Zhang, T.; Zscheischler, J. Identifying meteorological drivers of extreme impacts: An application to simulated crop yields. Earth Syst. Dyn. 2021, 12, 151–172. [Google Scholar] [CrossRef]
- Hovenden, N.W. Seasonal not annual rainfall determines grassland biomass response to carbon dioxide. Nature 2014, 511, 583–586. [Google Scholar] [CrossRef] [PubMed]
- Hoover, D.L.; Rogers, B.M. Not all droughts are created equal: The impacts of interannual drought pattern and magnitude on grassland carbon cycling. Glob. Change Biol. 2016, 22, 1809–1820. [Google Scholar] [CrossRef]
- Huang, M.; Wang, X.; Keenan, T.F.; Piao, S. Drought timing influences the legacy of tree growth recovery. Glob. Change Biol. 2018, 24, 3546–3559. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Rich, P.M.; Price, K.P. Temporal responses of NDVI to precipitation and temperature in the central Great Plains, USA. Int. J. Remote Sens. 2003, 24, 2345–2364. [Google Scholar] [CrossRef]
- Delgado-Balbuena, J.; Arredondo, J.T.; Loescher, H.W.; Pineda-Martínez, L.F.; Carbajal, J.N.; Vargas, R. Seasonal precipitation legacy effects determine the carbon balance of a semiarid grassland. J. Geophys. Res. Biogeosciences 2019, 124, 987–1000. [Google Scholar] [CrossRef]
- Pei, Z.; Fang, S.; Yang, W.; Wang, L.; Wu, M.; Zhang, Q.; Han, W.; Khoi, D.N. The Relationship between NDVI and Climate Factors at Different Monthly Time Scales: A Case Study of Grasslands in Inner Mongolia, China (1982–2015). Sustainability 2019, 11, 7243. [Google Scholar] [CrossRef] [Green Version]
- Anderegg, W.R.L.; Trugman, A.T.; Badgley, G.; Konings, A.G.; Shaw, J. Divergent forest sensitivity to repeated extreme droughts. Nat. Clim. Change 2020, 10, 1091–1095. [Google Scholar] [CrossRef]
- Kannenberg, S.A.; Schwalm, C.R.; Anderegg, W.R.L. Ghosts of the past: How drought legacy effects shape forest functioning and carbon cycling. Ecol. Lett. 2020, 23, 891–901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bastos, A.; Orth, R.; Reichstein, M.; Ciais, P.; Viovy, N.; Zaehle, S.; Anthoni, P.; Arneth, A.; Gentine, P.; Joetzjer, E.; et al. Vulnerability of European ecosystems to two compound dry and hot summers in 2018 and 2019. Earth Syst. Dyn. 2021, 12, 1015–1035. [Google Scholar] [CrossRef]
- Craine, J.M.; Nippert, J.B.; Elmore, A.J.; Skibbe, A.M.; Hutchinson, S.L.; Brunsell, N.A. Timing of climate variability and grassland productivity. Proc. Natl. Acad. Sci. USA 2012, 109, 3401–3405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eckes-Shephard, A.H.; Tiavlovsky, E.; Chen, Y.; Fonti, P.; Friend, A.D. Direct response of tree growth to soil water and its implications for terrestrial carbon cycle modelling. Glob. Change Biol. 2021, 27, 121–135. [Google Scholar] [CrossRef]
- Teasdale, J.R.; Cavigelli, M.A. Meteorological fluctuations define long-term crop yield patterns in conventional and organic production systems. Sci. Rep. 2017, 7, 688. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.A.; Shabanov, N.V.; Myneni, R.B. Variations in northern vegetation activity inferred from satellite data of vegetation index during 1981 to 1999. J. Geophys. Res. Atmos. 2001, 106, 20269–20283. [Google Scholar] [CrossRef]
- Butterfield, Z.; Buermann, W.; Keppel-Aleks, G. Satellite observations reveal seasonal redistribution of northern ecosystem productivity in response to interannual climate variability. Remote Sens. Environ. 2020, 242, 111755. [Google Scholar] [CrossRef]
- Zeng, L.; Wardlow, B.D.; Xiang, D.; Hu, S.; Li, D. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 11511. [Google Scholar] [CrossRef]
- Kern, A.; Marjanović, H.; Barcza, Z. Spring vegetation green-up dynamics in Central Europe based on 20-year long MODIS NDVI data. Agric. For. Meteorol. 2020, 287, 107969. [Google Scholar] [CrossRef]
- Kern, A.; Marjanović, H.; Csóka, G.; Móricz, N.; Pernek, M.; Hirka, A.; Matošević, D.; Paulin, M.; Kovač, G. Detecting the Oak lace bug infestation in oak forests using MODIS and meteorological data. Agric. For. Meteorol. 2021, 306, 108436. [Google Scholar] [CrossRef]
- Bonan, G.B.; Levis, S.; Kergoat, L.; Oleson, K.W. Landscapes as patches of plant functional types: An integrating concept for climate and ecosystem models. Glob. Biogeochem. Cycles 2002, 16, 5-1–5-23. [Google Scholar] [CrossRef] [Green Version]
- Černecký, J.; Gajdoš, P.; Špulerová, J.; Halada, Ľ.; Mederly, P.; Ulrych, L.; Ďuricová, V.; Švajda, J.; Černecká, Ľ.; Andráš, P.; et al. Ecosystems in Slovakia. J. Maps 2019, 16, 28–35. [Google Scholar] [CrossRef] [Green Version]
- Vačkář, D.; Grammatikopoulou, I.; Daněk, J.; Lorencová, E. Methodological aspects of ecosystem service valuation at the national level. One Ecosyst. 2018, 3, e25508. [Google Scholar] [CrossRef]
- Bardi, A.; Papini, P.; Quaglino, E.; Biondi, E.; Topić, J.; Milović, M.; Pandža, M.; Kaligarič, M.; Oriolo, G.; Roland, V.; et al. Karta prirodnih i poluprirodnih ne-šumskih kopnenih i slatkovodnih staništa Republike Hrvatske. AGRISTUDIO Srl TEMI Srl TIMESIS Srl Hrvat. Agencija Za Okoliš I Prir. Zagreb. 2016, p. 56. Available online: http://www.haop.hr/sites/default/files/uploads/dokumenti/03_prirodne/projekti/NIP-projekt_zavrsno_izvjesce.pdf (accessed on 3 July 2022).
- Tanács, E.; Belényesi, M.; Lehoczki, R.; Pataki, R.; Petrik, O.; Standovár, T.; Pásztor, L.; Laborczi, A.; Szatmári, G.; Molnár, Z.; et al. A national, high-resolution ecosystem basemap: Methodology, validation, and possible uses. Term. Közl. 2019, 25, 34–58. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef] [Green Version]
- Mátyás, C.; Berki, I.; Bidló, A.; Csóka, G.; Czimber, K.; Führer, E.; Gálos, B.; Gribovszki, Z.; Illés, G.; Hirka, A.; et al. Sustainability of Forest Cover under Climate Change on the Temperate-Continental Xeric Limits. Forests 2018, 9, 489. [Google Scholar] [CrossRef] [Green Version]
- Barcza, Z.; Bondeau, A.; Churkina, G.; Ciais, P.; Czóbel, S.; Gelybó, G.; Grosz, B.; Haszpra, L.; Hidy, D.; Horváth, L.; et al. Modeling of biosphere-atmosphere exchange of greenhouse gases—Model based biospheric greenhouse gas balance of Hungary. In Atmospheric Greenhouse Gases: The Hungarian Perspective; Haszpra, L., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 295–330. ISBN 978-90-481-9949-5. [Google Scholar] [CrossRef]
- EC, European Commission, Directorate-General for Environment; Sundseth, K. Natura 2000 in the Pannonian Region; Publications Office: Luxemburg, Belgium, 2010; ISBN 978-92-79-22586-8. [Google Scholar] [CrossRef]
- Lakatos, M.; Bihari, Z.; Izsák, B.; Szentes, O. Globális és hazai éghajlati trendek, szélsőségek változása: 2020-as helyzetkép. (Global trends and climate change in Hungary in 2020). Sci. Et Secur. 2021, 2, 164–171. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled Seamless SRTM Data V4. International Centre for Tropical Agriculture (CIAT). 2008. Available online: http://srtm.csi.cgiar.org (accessed on 20 May 2021).
- LP DAAC (Land Processes Distributed Active Archive Center). MOD09A1, Collection 6. NASA EOSDIS Land Processes DAAC, USGS Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota. Available online: https://lpdaac.usgs.gov (accessed on 14 February 2021).
- Vermote, E. MOD09A1 MODIS/Terra Surface Reflectance 8-Day L3 Global 500m SIN Grid V006 [Data Set]; NASA EOSDIS Land Processes DAAC: Reston, VA, USA, 2015. [Google Scholar] [CrossRef]
- Viovy, N.; Arino, O.; Belward, A.S. The Best Index Slope Extraction: A method for reducing noise in NDVI time-series. Int. J. Remote Sens. 1992, 13, 1585–1590. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Glassy, J.; Privette, J.L.; Tian, Y.; Lotsch, A.; Zhang, Y.; Wang, Y.; Morisette, J.T.; Votava, P.; Myneni, R.B.; et al. MODIS Leaf Area Index (LAI) and Fraction of Photosynthetically Active Radiation Absorbed by Vegetation (FPAR) Product (MOD15) Algorithm Theoretical Basis Document. 1999. Available online: https://lpdaac.usgs.gov/documents/90/MOD15_ATBD.pdf (accessed on 15 July 2021).
- Myneni, R.; Knyazikhin, Y.; Park, T. MOD15A2H MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500m SIN Grid V006 [Data set]; NASA EOSDIS Land Processes DAAC: Reston, VA, USA, 2015. [Google Scholar] [CrossRef]
- Dobor, L.; Barcza, Z.; Hlásny, T.; Havasi, Á.; Horváth, F.; Ittzés, P.; Bartholy, J. Bridging the gap between climate models and impact studies: The FORESEE Database. Geosci. Data J. 2015, 2, 1–11. [Google Scholar] [CrossRef]
- FORESEE Database. Available online: https://nimbus.elte.hu/FORESEE/ (accessed on 20 May 2021).
- CCCS. Copernicus Climate Change Service: ERA5-Land Hourly Data from 2001 to Present [Data Set]; ECMWF: Reading, UK, 2019. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Kern, A.; Marjanović, H.; Barcza, Z. Evaluation of the quality of NDVI3g dataset against Collection 6 MODIS NDVI in Central-Europe between 2000 and 2013. Remote Sens. 2016, 8, 955. [Google Scholar] [CrossRef] [Green Version]
- NÖSZTÉP Ecosystem Map of Hungary. Available online: https://alapterkep.termeszetem.hu/ (accessed on 14 November 2020).
- Wolfe, R.E.; Nishihama, M.; Fleig, A.J.; Kuyper, J.A.; Roy, D.P.; Storey, J.C.; Patt, F.S. Achieving sub-pixel geolocation accuracy in support of MODIS land science. Remote Sens. Environ. 2002, 83, 31–49. [Google Scholar] [CrossRef]
- Tan, B.; Woodcock, C.E.; Hu, J.; Zhang, P.; Ozdogan, M.; Huang, D.; Yang, W.; Knyazikhin, Y.; Myneni, R.B. The impact of gridding artifacts on the local spatial properties of MODIS data: Implications for validation, compositing, and band-to-band registration across resolutions. Remote Sens. Environ. 2006, 105, 98–114. [Google Scholar] [CrossRef]
- EEA. Co ORdinated INformation on the Environment (CORINE) Land Cover 2012, Version 18.4, European Commission—Directorate-General for Internal Market, Industry, Entrepreneurship and SMEs (DG-GROW, Data Owner); European Environment Agency (EEA, data custodian): Copenhagen, Denmark, 2016; Available online: http://land.copernicus.eu/pan-european/corine-land-cover/clc-2012 (accessed on 24 February 2020).
- Zhou, H.; Shao, J.; Liu, H.; Du, Z.; Zhou, L.; Liu, R.; Bernhofer, C.; Grünwald, T.; Dušek, J.; Montagnani, L.; et al. Relative importance of climatic variables, soil properties and plant traits to spatial variability in net CO2 exchange across global forests and grasslands. Agric. For. Meteorol. 2021, 307, 108506. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Santos, J.A.; Malheiro, A.C.; Karremann, M.K.; Pinto, J.G. Statistical modelling of grapevine yield in the Port Wine region under present and future climate conditions. Int. J. Biometeorol. 2011, 55, 119–131. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 9 January 2020).
- Keresztesi, B. (Ed.) The Black Locust; Akadémiai Kiadó: Budapest, Hungary, 1988; 197p, ISBN 963-05-4696-5. [Google Scholar]
- Kern, A.; Marjanović, H.; Dobor, L.; Anic, M.; Hlásny, T.; Barcza, Z. Identification of Years with Extreme Vegetation State in Central Europe Based on Remote Sensing and Meteorological Data. South East Eur. For. SEEFOR 2017, 8, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Zeng, H.; Jia, G.; Epstein, H. Recent changes in phenology over the northern high latitudes detected from multi-satellite data. Environ. Res. Lett. 2011, 6, 045508. [Google Scholar] [CrossRef] [Green Version]
- Buttler, A.; Mariotte, P.; Meisser, M.; Guillaume, T.; Signarbieux, C.; Vitra, A.; Preux, S.; Mercier, G.; Quezada, J.; Bragazza, L.; et al. Drought-induced decline of productivity in the dominant grassland species Lolium perenne L. depends on soil type and prevailing climatic conditions. Soil Biol. Biochem. 2019, 132, 47–57. [Google Scholar] [CrossRef]
- Kowalski, K.; Okujeni, A.; Brell, M.; Hostert, M. Quantifying drought effects in Central European grasslands through regression-based unmixing of intra-annual Sentinel-2 time series. Remote Sens. Environ. 2022, 268, 112781. [Google Scholar] [CrossRef]
- Reinermann, S.; Asam, S.; Kuenzer, C. Remote sensing of grassland production and management—A review. Rem. Sens. 2020, 12, 1949. [Google Scholar] [CrossRef]
- Wood, D.J.; Powell, S.L.; Stoy, P.C.; Thurman, L.L.; Beever, E.A. Is the grass always greener? Land surface phenology reveals differences in peak and season-long vegetation productivity responses to climate and management. Ecol. Evol. 2021, 11, 11168–11199. [Google Scholar] [CrossRef] [PubMed]
- Hofer, D.; Suter, M.; Haughey, E.; Finn, J.A.; Hoekstra, N.J.; Buchmann, N.; Lüscher, A. Yield of temperate forage grassland species is either largely resistant or resilient to experimental summer drought. J. Appl. Ecol. 2016, 53, 1023–1034. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Ficklin, D.; Manzoni, S.; Wang, L.; Way, D.; Phillips, R.; Novick, K.A. Response of ecosystem intrinsic water use efficiency and gross primary productivity to rising vapor pressure deficit. Environ. Res. Lett. 2019, 14, 074023. [Google Scholar] [CrossRef]
- Feng, X.; Fu, B.; Zhang, Y.; Pan, N.; Zeng, Z.; Tian, H.; Lyu, Y.; Chen, Y.; Ciais, P.; Wang, Y.; et al. Recent leveling off of vegetation greenness and primary production reveals the increasing soil water limitations on the greening Earth. Sci. Bull. 2021, 66, 1462–1471. [Google Scholar] [CrossRef]
- Yuan, W.; Zheng, Y.; Piao, S.; Ciais, P.; Lombardozzi, D.; Wang, Y.; Ryu, Y.; Chen, G.; Dong, W.; Hu, Z.; et al. Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 2019, 5, eaax1396. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.; Piao, S.; Ciais, P.; Myneni, R.; Chen, A.; Chevallier, F.; Dolman, A.J.; Janssens, I.A.; Peñuelas, J.; Zhang, G.; et al. Asymmetric effects of daytime and night-time warming on northern hemisphere vegetation. Nature 2013, 501, 88. [Google Scholar] [CrossRef]
- Xia, J.; Chen, J.; Piao, S.; Ciais, P.; Luo, Y.; Wan, S. Terrestrial carbon cycle affected by non-uniform climate warming. Nat. Geosci. 2014, 7, 173–180. [Google Scholar] [CrossRef]
- Tan, J.; Piao, S.; Chen, A.; Zeng, Z.; Ciais, P.; Janssens, I.A.; Mao, J.; Myneni, R.; Peng, S.; Peñuelas, J.; et al. Seasonally different response of photosynthetic activity to daytime and night-time warming in the northern hemisphere. Glob. Change Biol. 2014, 21, 377. [Google Scholar] [CrossRef]
- Wu, X.; Liu, H.; Li, X.; Liang, E.; Beck, P.S.A.; Huang, Y.M. Seasonal divergence in the interannual responses of northern hemisphere vegetation activity to variations in diurnal climate. Sci. Rep. 2016, 6, 19000. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Q.; Kong, D.; Singh, V.P.; Shi, P. Response of vegetation to different time-scales drought across China: Spatiotemporal patterns, causes and implications. Glob. Planet Change 2017, 152, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Ding, J.; Yang, T.; Zhao, Y.; Liu, D.; Wang, X.; Yao, Y.; Peng, S.; Wang, T.; Piao, S. Increasingly important role of atmospheric aridity on Tibetan alpine grasslands. Geophys. Res. Lett. 2018, 45, 2852–2859. [Google Scholar] [CrossRef]
- De Keersmaecker, W.; Lhermitte, S.; Tits, L.; Honnay, O.; Somers, B.; Coppin, P. Global vegetation resistance and resilience. Glob. Ecol. Biogeogr. 2015, 24, 539–548. [Google Scholar] [CrossRef]
- Gherardi, L.A.; Sala, O.E. Enhanced interannual precipitation variability increases plant functional diversity that in turn ameliorates negative impact on productivity. Ecol. Lett. 2015, 18, 1293–1300. [Google Scholar] [CrossRef]
- White, M.A.; Thornton, P.E.; Running, S.W.; Nemani, R.R. Parameterization and sensitivity analysis of the Biome-BGC terrestrial ecosystem model: Net primary production controls. Earth Interact. 2000, 4, 1–85. [Google Scholar] [CrossRef]
- Hidy, D.; Barcza, Z.; Marjanovic, H.; Ostrogovic Sever, M.Z.; Dobor, L.; Gelybó, G.; Fodor, N.; Pintér, K.; Churkina, G.; Running, S.; et al. Terrestrial ecosystem process model Biome-BGCMuSo v4.0: Summary of improvements and new modeling possibilities. Geosci. Model Dev. 2016, 9, 4405–4437. [Google Scholar] [CrossRef] [Green Version]
- Nagy, Z.; Pintér, K.; Czóbel, S.; Balogh, J.; Horváth, L.; Fóti, S.; Barcza, Z.; Weidinger, T.; Csintalan, Z.; Dinh, N.Q.; et al. The carbon budget of a semi-arid grassland in a wet and a dry year in Hungary. Agric. Ecosyst. Environ. 2007, 121, 21–29. [Google Scholar] [CrossRef]
- Verbesselt, J.; Robinson, A.; Stone, C.; Culvenor, D. Forecasting tree mortality using change metrics derived from MODIS satellite data. For. Ecol. Manag. 2009, 258, 1166–1173. [Google Scholar] [CrossRef]
- Kannenberg, S.A.; Novick, K.A.; Alexander, M.R.; Maxwell, J.T.; Moore, D.J.; Phillips, R.P.; Anderegg, W.R. Linking drought legacy effects across scales: From leaves to tree rings to ecosystems. Glob. Change Biol. 2019, 25, 2978–2992. [Google Scholar] [CrossRef]
- Wong, C.Y.S.; Young, D.J.N.; Latimer, A.M.; Buckley, T.N.; Magney, T.S. Importance of the legacy effect for assessing spatiotemporal correspondence between interannual tree-ring width and remote sensing products in the Sierra Nevada. Remote Sens. Environ. 2021, 265, 112635. [Google Scholar] [CrossRef]
- Hartmann, H. Carbon starvation during drought-induced tree mortality—Are we chasing a myth? J. Plant Hydraul. 2015, 2, e005. [Google Scholar] [CrossRef]
- Ruehr, N.K.; Grote, R.; Mayr, S.; Arneth, A. Beyond the extreme: Recovery of carbon and water relations in woody plants following heat and drought stress. Tree Physiol. 2019, 39, 1285–1299. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Beurs, K.M.; Townsend, P.A. Estimating the effect of gypsy moth defoliation using MODIS. Remote Sens. Environ. 2008, 112, 3983–3990. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef]
- Keenan, T.; Gray, J.; Friedl, M.A.; Toomey, M.; Bohrer, G.; Hollinger, D.; Munger, J.; O’Keefe, J.; Peter Schmid, H.; SueWing, I.; et al. Net carbon uptake has increased through warming-induced changes in temperate forest phenology. Nat. Clim. Chang. 2014, 4, 598–604. [Google Scholar] [CrossRef]
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- De Jong, R.; Verbesselt, J.; Schaepman, M.E.; de Bruin, S. Trend changes in global greening and browning: Contribution of short-term trends to longer-term change. Glob. Chang. Biol. 2012, 18, 642–655. [Google Scholar] [CrossRef]
- Forkel, M.; Carvalhais, N.; Verbesselt, J.; Mahecha, M.D.; Neigh, C.S.R.; Reichstein, M. Trend Change Detection in NDVI Time Series: Effects of Inter-Annual Variability and Methodology. Remote Sens. 2013, 5, 2113–2144. [Google Scholar] [CrossRef] [Green Version]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting Trend and Seasonal Changes in Satellite Image Time Series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- De Jong, R.; de Bruin, S.; de Wit, A.; Schaepman, M.E.; Dent, D.E. Analysis of monotonic greening and browning trends from global NDVI time-series. Remote Sens. Environ. 2011, 115, 692–702. [Google Scholar] [CrossRef] [Green Version]
- Ives, A.R.; Zhu, L.; Wang, F.; Zhu, J.; Morrow, C.J.; Radeloff, V.C. Statistical inference for trends in spatiotemporal data. Remote Sens. Environ. 2021, 266, 112678. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, C.B.; Band, L.E.; Sun, G.; Li, J. Reanalysis of global terrestrial vegetation trends from MODIS products: Browning or greening? Remote Sens. Environ. 2017, 191, 145–155. [Google Scholar] [CrossRef]








| Ecosystem Categories | Number of the Pixels | Mean of the Pixel-Level Share of the Given Category within the Pixels | Share in Hungary Based on the Used Pixels at 500 m (and all Possible at 20 m) | Altitudinal Distribution (Median, 5 and 95 Percentiles) |
|---|---|---|---|---|
| (1) Open sandy grassland | 11 | 99.4% | 0.01% (0.68%) | 117 m [106–144 m] |
| (2) Grassland on saline soil | 1086 | 99.4% | 1.01% (2.27%) | 86 m [83–93 m] |
| (3) Closed grassland on hard mountainous ground | 117 | 98.9% | 0.11% (4.91%) | 219 m [81–286 m] |
| (4) Beech | 192 | 98.5% | 0.18% (1.49%) | 586 m [262–879 m] |
| (5) Sessile oak with hornbeams | 210 | 98.6% | 0.19% (1.74%) | 400 m [242–530 m] |
| (6) Turkey oak | 115 | 97.6% | 0.11% (2.83%) | 293 m [216–435 m] |
| (7) Black locust dominated plantation | 42 | 97.7% | 0.04% (4.87%) | 139 m [112–210 m] |
| (8) All pedunculate oak (merged category) | 15 | 95.3% | 0.01% (1.67%) | 115 m [86–154 m] |
| Ecosystem Categories | Tmin | Tmax | Precipitation | SWC2 | Radiation | VPD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | Month | R | Month | R | Month | R | Month | R | Month | R | Month | |
| Positive correlation with NDVI | ||||||||||||
| Open sandy grassland | 0.68 | III | - | - | 0.76 | IX | 0.83 | VII–VIII | - | - | - | - |
| Grassland on saline soil | 0.72 | III | 0.71 | II–III | 0.83 | VIII-IX | 0.88 | VII | - | - | 0.61 | II–III |
| Closed grassland on hard m. ground | 0.76 | II–III | 0.72 | II–III | 0.85 | IX | 0.91 | IX–X | - | - | 0.55 | III–IV |
| Beech | 0.80 | X | 0.81 | X | - | - | - | - | 0.67 | IV–V | 0.75 | IV–V |
| Sessile oak with hornbeam | 0.78 | X | 0.81 | IV–V | 0.58 | X–XI | - | - | 0.62 | IV–V | 0.84 | IV–V |
| Turkey oak | 0.71 | X | 0.81 | IV–V | - | - | - | - | 0.65 | IV–V | 0.81 | IV–V |
| Black locust dominated plantation | 0.78 | II–III | 0.73 | II–III | 0.68 | IX | 0.66 | IX–X | - | - | 0.61 | III |
| All pedunculate oak | 0.78 | III–IV | 0.72 | III | - | - | - | - | - | - | 0.67 | IV–V |
| Negative correlation with NDVI | ||||||||||||
| Open sandy grassland | - | - | −0.75 | VIII–IX | - | - | - | - | −0.66 | VI–VII | −0.83 | VIII–IX |
| Grassland on saline soil | - | - | −0.80 | VIII–IX | - | - | - | - | −0.69 | VIII–IX | −0.83 | VIII–IX |
| Closed grassland on hard m. ground | - | - | −0.71 | V–VI | - | - | - | - | −0.59 | VIII–IX | −0.73 | V–VI |
| Beech | - | - | - | - | −0.77 | V | −0.72 | V–VI | - | - | - | - |
| Sessile oak with hornbeam | - | - | - | - | −0.75 | V | −0.60 | V–VI | −0.68 | XII | - | - |
| Turkey oak | - | - | - | - | −0.76 | V | −0.60 | V–VI | - | - | - | - |
| Black locust dominated plantation | - | - | - | - | - | - | - | - | −0.61 | II–III | −0.63 | IX |
| All pedunculate oak | - | - | - | - | - | - | - | - | - | - | - | - |
| Ecosystem Categories | Correlation | Tmin | Tmax | Precipitation | SWC2 | Radiation | VPD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lag (Days) | STSC | Lag (Days) | STSC | Lag (Days) | STSC | Lag (Days) | STSC | Lag (Days) | STSC | Lag (Days) | STSC | ||
| Open sandy grassland | negative | - | 0% | 42.5 | 32% | - | 0% | - | 0% | 34.3 | 34% | 38.4 | 49% |
| positive | 28.4 | 28% | - | 0% | 26.9 | 55% | 24.0 | 68% | - | 0% | - | 0% | |
| Grassland on saline soil | negative | - | 0% | 36.0 | 40% | - | 0% | - | 0% | 41.3 | 30% | 27.4 | 53% |
| positive | 30.4 | 13% | 28.0 | 10% | 36.0 | 70% | 24.6 | 73% | - | 0% | 32.0 | 5% | |
| Closed grassland on hard m. ground | negative | - | 0% | 37.3 | 30% | - | 0% | - | 0% | 40.7 | 38% | 12.6 | 35% |
| positive | 26.0 | 20% | 30.4 | 13% | 37.7 | 70% | 26.9 | 70% | - | 0% | 24.0 | 3% | |
| Beech | negative | - | 0% | - | 0% | 44.8 | 25% | 42.3 | 18% | 80.0 | 5% | - | 0% |
| positive | 34.7 | 45% | 35.0 | 40% | - | 0% | - | 0% | 32.0 | 10% | 35.7 | 38% | |
| Sessile oak with hornbeam | negative | - | 0% | - | 0% | 29.3 | 15% | 24.0 | 5% | 40.0 | 18% | - | 0% |
| positive | 29.8 | 28% | 28.9 | 33% | 40.0 | 8% | 50.7 | 8% | 32.0 | 5% | 24.0 | 23% | |
| Turkey oak | negative | - | 0% | - | 0% | 46.0 | 20% | 24.0 | 3% | 88.0 | 3% | - | 0% |
| positive | 28.8 | 25% | 25.8 | 23% | - | 0% | 40.0 | 3% | 52.0 | 10% | 42.4 | 33% | |
| Black locust dominated plantation | negative | 82.7 | 8% | 80.0 | 15% | - | 0% | - | 0% | 53.7 | 18% | 76.8 | 25% |
| positive | 30.1 | 53% | 43.6 | 23% | 33.1 | 18% | 38.4 | 25% | - | 0% | 32.0 | 5% | |
| All pedunculate oak | negative | - | 0% | - | 0% | 72 | 5% | 56 | 13% | 64.0 | 10% | - | 0% |
| positive | 40 | 40% | 25.8 | 23% | - | 0% | - | 0% | - | 0% | 24.0 | 13% | |
| NDVI | LAI | |||||||
|---|---|---|---|---|---|---|---|---|
| Ecosystem Categories | R2 | p | RMSE | bias | R2 | p | RMSE | bias |
| Open sandy grassland | 0.65 * | 0.000 | 0.046 | −0.001 | 0.58 * | 0.000 | 0.188 | 0.000 |
| Grassland on saline soil | 0.87 * | 0.000 | 0.036 | −0.001 | 0.81 * | 0.000 | 0.154 | −0.002 |
| Closed grassland on hard m. g. | 0.76 * | 0.000 | 0.037 | 0.000 | 0.77* | 0.000 | 0.151 | 0.000 |
| Beech | 0.36 * | 0.004 | 0.008 | 0.000 | # | |||
| Sessile oak with hornbeam | 0.10 | 0.161 | 0.015 | −0.001 | 0.43 * | 0.001 | 0.177 | 0.006 |
| Turkey oak | 0.40 * | 0.002 | 0.013 | 0.000 | 0.50 * | 0.000 | 0.176 | −0.001 |
| Black locust dominated p. | 0.32 * | 0.007 | 0.032 | −0.000 | 0.33 * | 0.006 | 0.470 | 0.006 |
| All pedunculate oak | 0.02 | 0.528 | 0.015 | 0.001 | # | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kern, A.; Barcza, Z.; Hollós, R.; Birinyi, E.; Marjanović, H. Critical Climate Periods Explain a Large Fraction of the Observed Variability in Vegetation State. Remote Sens. 2022, 14, 5621. https://doi.org/10.3390/rs14215621
Kern A, Barcza Z, Hollós R, Birinyi E, Marjanović H. Critical Climate Periods Explain a Large Fraction of the Observed Variability in Vegetation State. Remote Sensing. 2022; 14(21):5621. https://doi.org/10.3390/rs14215621
Chicago/Turabian StyleKern, Anikó, Zoltán Barcza, Roland Hollós, Edina Birinyi, and Hrvoje Marjanović. 2022. "Critical Climate Periods Explain a Large Fraction of the Observed Variability in Vegetation State" Remote Sensing 14, no. 21: 5621. https://doi.org/10.3390/rs14215621
APA StyleKern, A., Barcza, Z., Hollós, R., Birinyi, E., & Marjanović, H. (2022). Critical Climate Periods Explain a Large Fraction of the Observed Variability in Vegetation State. Remote Sensing, 14(21), 5621. https://doi.org/10.3390/rs14215621