Author Contributions
Conceptualization, M.K., F.T., D.B. and M.B.; methodology, M.K., F.T., D.B. and M.B.; software, M.K. and F.T.; validation, M.K., F.T., D.B. and M.B.; formal analysis, M.K. and F.T.; investigation, M.K. and F.T.; resources, M.B.; data curation, M.K. and F.T.; writing—original draft preparation, M.K. and F.T.; writing—review and editing, D.B. and M.B.; visualization, M.K. and F.T.; supervision, D.B. and M.B.; project administration, M.B.; funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Ground-based SAR geometry. Coordinates represent position of a point object in real space. In the dashed square, coordinates of the Fourier domain space or K-space are presented. is a wave vector coordinate in the range direction while is a wave vector coordinate in the x direction.
Figure 1.
Ground-based SAR geometry. Coordinates represent position of a point object in real space. In the dashed square, coordinates of the Fourier domain space or K-space are presented. is a wave vector coordinate in the range direction while is a wave vector coordinate in the x direction.
Figure 2.
Developed GBSAR-Pi.
Figure 2.
Developed GBSAR-Pi.
Figure 3.
GBSAR-Pi scheme.
Figure 3.
GBSAR-Pi scheme.
Figure 4.
RealSAR objects: aluminium, glass and plastic bottle, and GBSAR-Pi.
Figure 4.
RealSAR objects: aluminium, glass and plastic bottle, and GBSAR-Pi.
Figure 5.
Pairs of RealSAR-RAW (left) and RealSAR-IMG (right) examples. Example pair (a) represents an empty scene, (b) scene with an aluminium bottle, (c) scene with an aluminium and a glass bottle, while (d) contains all three bottles.
Figure 5.
Pairs of RealSAR-RAW (left) and RealSAR-IMG (right) examples. Example pair (a) represents an empty scene, (b) scene with an aluminium bottle, (c) scene with an aluminium and a glass bottle, while (d) contains all three bottles.
Figure 6.
The machine learning setup for all image and raw data models. For image-based classification, the dimensions of input images are (496, 369, 3). For raw data classification, the dimensions of the input matrix are (1024, 30, 1). All models produce three posterior probability distributions , where .
Figure 6.
The machine learning setup for all image and raw data models. For image-based classification, the dimensions of input images are (496, 369, 3). For raw data classification, the dimensions of the input matrix are (1024, 30, 1). All models produce three posterior probability distributions , where .
Figure 7.
Single-layer fully connected neural network classifier for raw data. The input matrix of dimensions (1024, 30, 1) is flattened into a vector of 30,720 elements. The vector is then fed to a fully connected classifier with the sigmoid activation function, which produces an output vector size 3 which represents three posterior probability distributions , where .
Figure 7.
Single-layer fully connected neural network classifier for raw data. The input matrix of dimensions (1024, 30, 1) is flattened into a vector of 30,720 elements. The vector is then fed to a fully connected classifier with the sigmoid activation function, which produces an output vector size 3 which represents three posterior probability distributions , where .
Figure 8.
Raw data classifier based on the long short term memory network. Since the LSTM is a sequential model, the input matrix with dimensions (1024, 30) is processed as a sequence of 30 vectors with size 1024. Each 1024-dimensional input vector is embedded into a 256-dim representation by a learned embedding layer (Emb). The dimension of the hidden state is 256. The bidirectional LSTM network aggregates the input sequence by processing it in two directions and concatenating the final hidden states for both directions. As with the fully connected classifier, the resulting vector is given to a fully connected classifier with the sigmoid activation function, which the three posterior probability distributions.
Figure 8.
Raw data classifier based on the long short term memory network. Since the LSTM is a sequential model, the input matrix with dimensions (1024, 30) is processed as a sequence of 30 vectors with size 1024. Each 1024-dimensional input vector is embedded into a 256-dim representation by a learned embedding layer (Emb). The dimension of the hidden state is 256. The bidirectional LSTM network aggregates the input sequence by processing it in two directions and concatenating the final hidden states for both directions. As with the fully connected classifier, the resulting vector is given to a fully connected classifier with the sigmoid activation function, which the three posterior probability distributions.
Figure 9.
All 17 convolutional layers and one fully-connected layer of the unmodified ResNet18 network. The convolutional layers are grouped into 5 groups: conv1, conv2, conv3, conv4, and conv5. There are four convolutional layers that downsample the input tensor by using a stride of 2. They are the first convolutional layers in groups conv1, conv3, conv4, and conv5. These layers are emphasized in the image. There is also a max pooling layer between groups conv1 and conv2, which also downsamples the image by using a stride of 2. Since the input image is downsampled five times, the resulting tensor which is output by the final convolutional layer is 32 times smaller in both spatial dimensions than the input image.
Figure 9.
All 17 convolutional layers and one fully-connected layer of the unmodified ResNet18 network. The convolutional layers are grouped into 5 groups: conv1, conv2, conv3, conv4, and conv5. There are four convolutional layers that downsample the input tensor by using a stride of 2. They are the first convolutional layers in groups conv1, conv3, conv4, and conv5. These layers are emphasized in the image. There is also a max pooling layer between groups conv1 and conv2, which also downsamples the image by using a stride of 2. Since the input image is downsampled five times, the resulting tensor which is output by the final convolutional layer is 32 times smaller in both spatial dimensions than the input image.
Figure 10.
The spatial dimensions of the input raw data matrix and subsequent subsampled intermediate representations after each group of convolutional layers. For groups conv1, conv3, conv4, and conv5, the subsampling is completed in the first convolutional layer of the group. For group conv2, the subsampling is completed in the max pooling layer immediately before the first convolutional layer of conv2. The first diagram show how, without any modification to the ResNet18 architecture, both the vertical and horizontal dimensions are halved five times. The vertical dimension is downsampled from 1024 to 32, while the horizontal dimension is downsampled from 30 to 1. The second diagram shows how only the vertical dimension is subsampled after our modification to the ResNet18 architecture, while the horizontal dimension remains constant. This is because our modification sets the horizontal stride of subsampling layers to 1. Note that the dimensions in the figure are not to scale due to impracticality of displaying very tall and narrow matrices.
Figure 10.
The spatial dimensions of the input raw data matrix and subsequent subsampled intermediate representations after each group of convolutional layers. For groups conv1, conv3, conv4, and conv5, the subsampling is completed in the first convolutional layer of the group. For group conv2, the subsampling is completed in the max pooling layer immediately before the first convolutional layer of conv2. The first diagram show how, without any modification to the ResNet18 architecture, both the vertical and horizontal dimensions are halved five times. The vertical dimension is downsampled from 1024 to 32, while the horizontal dimension is downsampled from 30 to 1. The second diagram shows how only the vertical dimension is subsampled after our modification to the ResNet18 architecture, while the horizontal dimension remains constant. This is because our modification sets the horizontal stride of subsampling layers to 1. Note that the dimensions in the figure are not to scale due to impracticality of displaying very tall and narrow matrices.
![Remotesensing 14 05673 g010]()
Figure 11.
The transformation of a multi-class confusion matrix into a binary confusion matrix for class
. The macro-
score is calculated as the arithmetic mean of
scores of all classes [
60].
Figure 11.
The transformation of a multi-class confusion matrix into a binary confusion matrix for class
. The macro-
score is calculated as the arithmetic mean of
scores of all classes [
60].
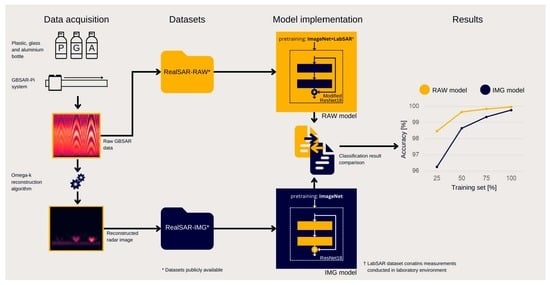
Figure 12.
Average test mAP of the RAW and IMG pair of models for each combination of weight initialization scheme and training set size.
Figure 12.
Average test mAP of the RAW and IMG pair of models for each combination of weight initialization scheme and training set size.
Figure 13.
Confusion matrices for the best IMG and RAW models. E—Empty, A—Aluminium, P—Plastic, and G—Glass.
Figure 13.
Confusion matrices for the best IMG and RAW models. E—Empty, A—Aluminium, P—Plastic, and G—Glass.
Figure 14.
RealSAR-RAW (left) and RealSAR-IMG (right) misclassified examples. Example (a) is misclassified by the IMG model while example (b) is misclassified by both RAW and IMG models. In (a) the recorded scene included a glass bottle, but IMG model classified it as plastic bottle. In (b) the recorded scene included an aluminium and a plastic bottle but both models classified it as scene with an aluminium bottle only.
Figure 14.
RealSAR-RAW (left) and RealSAR-IMG (right) misclassified examples. Example (a) is misclassified by the IMG model while example (b) is misclassified by both RAW and IMG models. In (a) the recorded scene included a glass bottle, but IMG model classified it as plastic bottle. In (b) the recorded scene included an aluminium and a plastic bottle but both models classified it as scene with an aluminium bottle only.
Table 1.
LabSAR and RealSAR measurement set comparison. First five rows describe objects and scenes, while others GBSAR-Pi parameters used in the measurements.
Table 1.
LabSAR and RealSAR measurement set comparison. First five rows describe objects and scenes, while others GBSAR-Pi parameters used in the measurements.
| | LabSAR | RealSAR |
|---|
| Objects (# of measurements) | big (37) and small (70) metalized box, and bottle of water (43) | aluminium (172), glass (172) and plastic (179) bottle |
| # of scene combinations | 3 | 8 |
| Object distance [cm] | 100 | between 20 and 70 |
| Object position | center | various |
| # of images | 150 | 338 |
| Azimuth step size [cm] | 0.4 | 1 |
| Azimuth points | 160 | 30 |
| Total aperture length [cm] | 64 | 30 |
| Range resolution [cm] | 21.4 | 21.4 |
| Polarization | HH | HH and VV |
| FMCW central frequency [GHz] | 24 | 24 |
| Bandwidth [MHz] | 700 | 700 |
| Chirp duration [ms] | 166 | 166 |
| Frequency points | 1024 | 1024 |
| Time per measurement [min] | 15 | 4 |
Table 2.
Comparison of performance of all raw data models with and without jittering. The metric used is mean average precision (mAP).
Table 2.
Comparison of performance of all raw data models with and without jittering. The metric used is mean average precision (mAP).
| Augmentation | Model |
|---|
| FC | LSTM | MNv3 | RN18 | RAW-RN18 |
|---|
| No jittering | 90.89 | 92.51 | 96.07 | 96.95 | 99.51 |
| With Jittering | 90.97 | 92.87 | 6.23 | 97.12 | 99.73 |
Table 3.
Comparison of performance of all considered raw and image-based classification models in combination with all different weight initialization procedures on the validation set. The metric used is mean average precision (mAP).
Table 3.
Comparison of performance of all considered raw and image-based classification models in combination with all different weight initialization procedures on the validation set. The metric used is mean average precision (mAP).
| Input Type | Model | Weight Initialization |
|---|
| Random | ImageNet | LabSAR | ImageNet + LabSAR |
|---|
| RAW | MNv3 | 96.23 | 96.59 | 96.31 | 96.39 |
| RN18 | 97.12 | 97.42 | 97.27 | 97.38 |
| RAW-RN18 | 99.73 | 99.71 | 99.67 | 99.95 |
| IMG | MNv3 | 98.29 | 98.71 | 98.34 | 98.66 |
| RN18 | 99.35 | 99.75 | 99.04 | 99.64 |
Table 4.
Comparison of performance of the two best model configurations for image and raw data classification. The chosen image model was an unmodified ResNet18 (RN18), while the chosen raw data model was a ResNet18 with our modification which prevents horizontal subsampling (RAW-RN18). We compare the two models across different weight initialization procedures and training set sizes on the validation set. The metric used is mean average precision (mAP).
Table 4.
Comparison of performance of the two best model configurations for image and raw data classification. The chosen image model was an unmodified ResNet18 (RN18), while the chosen raw data model was a ResNet18 with our modification which prevents horizontal subsampling (RAW-RN18). We compare the two models across different weight initialization procedures and training set sizes on the validation set. The metric used is mean average precision (mAP).
| Model | Training Set Size |
|---|
| 0.25 | 0.5 | 0.75 | Full |
|---|
| IMG, RN18, random | 96.56 | 98.72 | 99.33 | 99.35 |
| IMG, RN18, ImageNet | 96.25 | 98.63 | 99.33 | 99.75 |
| IMG, RN18, LabSAR | 98.07 | 99.65 | 99.03 | 99.04 |
| IMG, RN18, ImageNet + LabSAR | 96.56 | 98.94 | 99.31 | 99.64 |
| RAW, RAW-RN18, random | 98.25 | 99.13 | 99.66 | 99.73 |
| RAW, RAW-RN18, ImageNet | 98.66 | 99.51 | 99.60 | 99.71 |
| RAW, RAW-RN18, LabSAR | 98.74 | 98.89 | 99.23 | 99.67 |
| RAW, RAW-RN18, ImageNet + LabSAR | 98.45 | 99.63 | 99.82 | 99.95 |
Table 5.
Per-class AP performance of the best IMG and RAW models on the test set.
Table 5.
Per-class AP performance of the best IMG and RAW models on the test set.
| | Aluminium | Plastic | Glass | Mean |
|---|
| IMG, ImageNet | 98.07 | 97.42 | 98.07 | 97.85 |
| RAW, ImageNet + LabSAR | 98.71 | 98.12 | 97.85 | 98.23 |
Table 6.
Per-class F1 scores and the macro F1 score for the best threshold values on the validation set. E—Empty, A—Aluminium, P—Plastic, and G—Glass.
Table 6.
Per-class F1 scores and the macro F1 score for the best threshold values on the validation set. E—Empty, A—Aluminium, P—Plastic, and G—Glass.
| | E | A | P | G | A, P | A, G | G, P | A, G, P | Mean |
|---|
| IMG, ImageNet | 90.91 | 100 | 83.33 | 87.50 | 94.12 | 100 | 100 | 100 | 94.48 |
| RAW, ImageNet + LabSAR | 90.91 | 93.33 | 95.24 | 94.74 | 100 | 100 | 100 | 100 | 96.78 |
Table 7.
Per-class F1 scores and the macro F1 score of the two best models and their ensemble on the test set. Classes: E—Empty, A—Aluminium, P—Plastic, and G—Glass.
Table 7.
Per-class F1 scores and the macro F1 score of the two best models and their ensemble on the test set. Classes: E—Empty, A—Aluminium, P—Plastic, and G—Glass.
| | E | A | P | G | A, P | A, G | G, P | A, G, P | Mean |
|---|
| IMG, ImageNet | 80.00 | 66.67 | 78.26 | 93.33 | 88.89 | 75.00 | 94.74 | 94.12 | 83.88 |
| RAW, ImageNet + LabSAR | 83.33 | 75.00 | 90.00 | 94.12 | 94.12 | 87.50 | 81.82 | 100.00 | 88.24 |
| Ensemble | 81.12 | 71.12 | 82.55 | 93.33 | 91.25 | 79.73 | 86.74 | 97.24 | 85.39 |