Generating Daily Land Surface Temperature Downscaling Data Based on Sentinel-3 Images
Abstract
:1. Introduction
2. Study Sites and Datasets
2.1. Study Sites
- Site 1—Beijing
- Site 2—Guilin
- Site 3—Xi’an–Xian Yang
- Site 4—Taihu River Basin
2.2. Data and Data Processing
3. Methods
3.1. Downscaling Model
3.2. Methodological Workflow
3.3. Generalized Single-Channel Algorithm
3.4. Downscaling Model Performance Evaluation
4. Results
4.1. Qualitative Evaluation
4.1.1. Qualitative Evaluation of Different Sites
4.1.2. Qualitative Evaluation of Different Seasons
4.2. Quantitative Evaluation
4.2.1. Comparison with Landsat 8 LST Data
4.2.2. Comparison with Sentinel-3 SLSTR LST Data
5. Discussion
5.1. Limitations of the Linear Regression Model
5.2. Limitations of the Verification Methods of the Downscaling Models
5.3. Uncertainties from the Resampling Algorithms
5.4. Uncertainties of the Remote Sensing Data
6. Conclusions
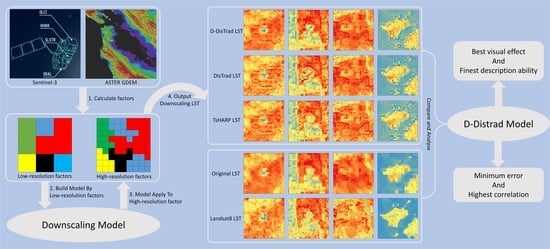
- Comparing the D-DisTrad model to the DisTrad model and TsHARP model, the D-DisTrad model displayed a higher PCC and , lower MAE and RMSE, and a good MB value (the PCC values varied from 0.938 to 0.994, the values ranged from 0.889 to 0.989, the MAE values were within the range of 0.103 to 0.891 K, the RMSE values were in the range of 0.220 to 1.235 K, and the MB values were within the limits of 0.001 to 0.022 K) as compared to the DisTrad model (the PCC values varied from 0.876 to 0.983, the values ranged from 0.767 to 0.967, the MAE values were within the range of 0.220 to 0.984 K, the RMSE values were in the range of 0.380 to 1.410 K, and the MB values were within the limits of 0.001 to 0.019 K) and TsHARP model (the PCC values varied from 0.871 to 0.984, the values ranged from 0.759 to 0.967, the MAE values were within the range of 0.205 to 1.058 K, the RMSE values were in the range of 0.379 to 1.448 K, and the MB values were within the limits of 0.003 to 0.210 K), which suggested a better performance by using the D-DisTrad model to obtain downscaled LST data;
- The D-DisTrad model is completely based on the Sentinel-3 platform and ASTER GDEM data. In this paper, multispectral bands of OLCI sensor and ASTER GDEM data were used to construct the influence factors of independent variables and the regression analysis was carried out with the LST band of the SLSTR sensor, then the construction of the D-DisTrad model was completed. The advantages and significance of this model come from its ability to perform all downscaling tasks using the Sentinel-3 images alone, without relying again on the data from other satellite platforms to provide multispectral or LST images. ASTER GDEM data are also stable. Meanwhile, thanks to the high temporal resolution of the Sentinel-3 platform, the D-DisTrad model not only has higher prediction accuracy but also has a higher temporal resolution and can provide 300 m spatial resolution LST data at the daily scale, which has great advantages for LST research on the daily scale;
- The inaccuracy of the satellite data itself, the error of the satellite data processing process, and the choice and error of the resampling algorithms will affect the precision of the downscaling results. As the largest residuals source in the verification of downscaling results, areas with major topographic variations and complex land covers have a significant impact on the downscaling results. All of them prove that it is necessary to further optimize and reconstruct the model, and it is also worth paying attention to evaluating the results using ground-based measured LST data;
- With the development of machine learning, machine-learning-based methods have been applied to the study of LST downscaling. The D-DisTrad model proposed in this paper has largely achieved better qualitative and quantitative evaluation results when compared to other linear regression models. A comparison of the downscaling results obtained from the linear regression model-based approach and the machine-learning-based approach for the Sentinel-3 data and the impact factors used in this paper’s model is also well worth the next step, and the results of the comparison may also have implications for how the linear regression model can be improved;
- The SLSTR sensor’s excellent temporal resolution enables it to capture images not only during the day but again at night on the same day. Therefore, two LST data scenes—one for the day and one for the night—can be generated in a single day. If it is considered that the topography and land cover of the study sites are unchanged on the same day, D-DisTrad can also be used to generate nighttime LST downscaling data, which are of great significance and have good prospects for studying the changes in day and night LST data and for related research under long time series.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheval, S.; Dumitrescu, A. The summer surface urban heat island of Bucharest (Romania) retrieved from MODIS images. Theor. Appl. Climatol. 2014, 121, 631–640. [Google Scholar] [CrossRef]
- Dihkan, M.; Karsli, F.; Guneroglu, A.; Guneroglu, N. Evaluation of surface urban heat island (SUHI) effect on coastal zone: The case of Istanbul Megacity. Ocean Coast Manag. 2015, 118, 309–316. [Google Scholar] [CrossRef]
- Schwarz, N.; Schlink, U.; Franck, U.; Großmann, K. Relationship of land surface and air temperatures and its implications for quantifying urban heat island indicators—An application for the city of Leipzig (Germany). Ecol. Indic. 2012, 18, 693–704. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. Thermal remote sensing for examining the relationship between urban Land surface Temperature and land use/cover in Tabriz city, Iran. In Proceedings of the International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; IEEE: New York, NY, USA, 2012; pp. 2229–2232. [Google Scholar] [CrossRef]
- Gazi, M.Y.; Rahman, M.Z.; Uddin, M.M.; Rahman, F.M.A. Spatio-temporal dynamic land cover changes and their impacts on the urban thermal environment in the Chittagong metropolitan area, Bangladesh. GeoJournal 2020, 86, 2119–2134. [Google Scholar] [CrossRef]
- Maffei, C.; Alfieri, S.M.; Menenti, M. Relating Spatiotemporal Patterns of Forest Fires Burned Area and Duration to Diurnal Land Surface Temperature Anomalies. Remote Sens. 2018, 10, 1777. [Google Scholar] [CrossRef] [Green Version]
- Maffei, C.; Lindenbergh, R.; Menenti, M. Combining multi-spectral and thermal remote sensing to predict forest fire characteristics. ISPRS J. Photogramm. Remote Sens. 2021, 181, 400–412. [Google Scholar] [CrossRef]
- Abdullah, H.; Omar, D.K.; Polat, N.; Bilgili, A.V.; Sharef, S.H. A comparison between day and night land surface temperatures using acquired satellite thermal infrared data in a winter wheat field. Remote Sens. Appl. 2020, 19, 100368. [Google Scholar] [CrossRef]
- Islam, S.; Ma, M. Geospatial Monitoring of Land Surface Temperature Effects on Vegetation Dynamics in the Southeastern Region of Bangladesh from 2001 to 2016. ISPRS Int. J. Geoinf. 2018, 7, 486. [Google Scholar] [CrossRef] [Green Version]
- Cammalleri, C.; Vogt, J. On the Role of Land Surface Temperature as Proxy of Soil Moisture Status for Drought Monitoring in Europe. Remote Sens. 2015, 7, 16849–16864. [Google Scholar] [CrossRef]
- Chi, Y.; Sun, J.; Sun, Y.; Liu, S.; Fu, Z. Multi-temporal characterization of land surface temperature and its relationships with normalized difference vegetation index and soil moisture content in the Yellow River Delta, China. Glob. Ecol. Conserv. 2020, 23, e01092. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Cao, X.; Bao, A.; Li, L. A Study of Retrieval Land Surface Temperature and Evapotranspiration in Response to LUCC Based on Remote Sensing Data in Sanggong River. In Proceedings of the International Conference on Environmental Science and Information Application Technology, Wuhan, China, 4–5 July 2009; pp. 325–329. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index–radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Zhou, D.; Xiao, J.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.; Frolking, S.; Yao, R.; Qiao, Z.; Sobrino, J.A. Satellite Remote Sensing of Surface Urban Heat Islands: Progress, Challenges, and Perspectives. Remote Sens. 2019, 11, 48. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.; Xiao, J.; Li, X.; Zhou, D.; Wu, Y. Combining GOES-R and ECOSTRESS land surface temperature data to investigate diurnal variations of surface urban heat island. Sci. Total Environ. 2022, 823, 153652. [Google Scholar] [CrossRef]
- Hulley, G.C.; Gottsche, F.M.; Rivera, G.; Hook, S.J.; Freepartner, R.J.; Martin, M.A.; Cawse-Nicholson, K.; Johnson, W.R. Validation and Quality Assessment of the ECOSTRESS Level-2 Land Surface Temperature and Emissivity Product. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5000523. [Google Scholar] [CrossRef]
- Zhan, W.; Chen, Y.; Zhou, J.; Wang, J.; Liu, W.; Voogt, J.; Zhu, X.; Quan, J.; Li, J. Disaggregation of remotely sensed land surface temperature: Literature survey, taxonomy, issues, and caveats. Remote Sens. Environ. 2013, 131, 119–139. [Google Scholar] [CrossRef]
- Li, N.; Wu, H.; Luan, Q. Land surface temperature downscaling in urban area: A case study of Beijing. J. Remote Sens. 2021, 25, 1808–1820. [Google Scholar] [CrossRef]
- Yoo, C.; Im, J.; Park, S.; Cho, D. Spatial Downscaling of MODIS Land Surface Temperature: Recent Research Trends, Challenges, and Future Directions. Korean J. Remote Sens. 2020, 36, 609–626. [Google Scholar] [CrossRef]
- Yang, Y.; Cao, C.; Pan, X.; Li, X.; Zhu, X. Downscaling Land Surface Temperature in an Arid Area by Using Multiple Remote Sensing Indices with Random Forest Regression. Remote Sens. 2017, 9, 789. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Gao, W.; Peng, W. Downscale MODIS Land Surface Temperature Based on Three Different Models to Analyze Surface Urban Heat Island: A Case Study of Hangzhou. Remote Sens. 2020, 12, 2134. [Google Scholar] [CrossRef]
- Feng, G.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M.U. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Li, X.; Jiang, T.; Xin, X.; Zhang, H.; Liu, Q. Spatial downscaling of land surface temperature based on MODIS data. Chin. J. Ecol. 2016, 35, 3443–3450. [Google Scholar] [CrossRef]
- Yang, Y.; Li, X.; Cao, C. Downscaling urban land surface temperature based on multi-scale factor. Sci. Surv. Mapp. 2017, 42, 73–79. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, R.; Qian, J.; Dang, C.; Yue, H. Land Surface Temperature Downscaling Based on Multiple Factors. Remote Sens. Inf. 2020, 35, 6–18. [Google Scholar] [CrossRef]
- Wang, Q.; Atkinson, P.M. Spatio-temporal fusion for daily Sentinel-2 images. Remote Sens. Environ. 2018, 204, 31–42. [Google Scholar] [CrossRef] [Green Version]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with Erts. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1974; p. 309. [Google Scholar]
- McFEETERS, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Escadafal, R. Remote sensing of arid soil surface color with Landsat thematic mapper. Adv. Space Res. 1989, 9, 159–163. [Google Scholar] [CrossRef]
- Guo, L.J.; Moore, J.M. Pixel block intensity modulation: Adding spatial detail to TM band 6 thermal imagery. Int. J. Remote Sens. 2010, 19, 2477–2491. [Google Scholar] [CrossRef]
- Zhao, G.; Xue, H.; Feng, L. Assessment of ASTER GDEM Performance by Comparing with SRTM and ICESat/GLAS Data in Central China. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010. [Google Scholar] [CrossRef]
- Huryna, H.; Cohen, Y.; Karnieli, A.; Panov, N.; Kustas, W.P.; Agam, N. Evaluation of TsHARP Utility for Thermal Sharpening of Sentinel-3 Satellite Images Using Sentinel-2 Visual Imagery. Remote Sens. 2019, 11, 2304. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Ma, M.; Zhu, X.; Ge, W. Research on spatial characteristics of metropolis development using nighttime light data: NTL based spatial characteristics of Beijing. PLoS ONE 2020, 15, e0242663. [Google Scholar] [CrossRef]
- Yan, H.; Zhou, G.; Lu, X. Comparative Analysis of Surface Soil Moisture Retrieval Using VSWI and TVDI in Karst Areas. In Proceedings of the International Conference on Intelligent Earth Observing and Applications, Guilin, China, 9 December 2015. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Yin, J.; Cai, H.; Tian, P.; Tang, M. Spatial Downscaling Research of the Land Surface Temperature in Karst Region. Geogr. Geoinf. Sci. 2021, 37, 38–46,99. [Google Scholar] [CrossRef]
- Zhu, L.; Li, J.; Wu, C.; Yang, B.; Li, Q.; Gong, H. Comparison of LST retrieval algorithms between single-channel and split-windows for high-resolution infrared camera. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. I-25–I-28. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, L.; Ma, Y. Estimation of 30 m land surface temperatures over the entire Tibetan Plateau based on Landsat-7 ETM+ data and machine learning methods. Int. J. Digit. Earth 2022, 15, 1038–1055. [Google Scholar] [CrossRef]
- Arabi Aliabad, F.; Zare, M.; Ghafarian Malamiri, H. Comparison of the accuracy of daytime land surface temperature retrieval methods using Landsat 8 images in arid regions. Infrared. Phys. Technol. 2021, 115, 103692. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. Atmos. 2003, 108, 4688. [Google Scholar] [CrossRef] [Green Version]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Skokovic, D.; Mattar, C.; Cristobal, J. Land Surface Temperature Retrieval Methods From Landsat-8 Thermal Infrared Sensor Data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Chakraborty, T.C.; Lee, X.; Ermida, S.; Zhan, W. On the land emissivity assumption and Landsat-derived surface urban heat islands: A global analysis. Remote Sens. Environ. 2021, 265, 112682. [Google Scholar] [CrossRef]
- Qin, Z.; Li, W.; Gao, M.; Zhang, H. Estimation of land surface emissivity for Landsat TM6 and its application to Lingxian Region in north China. In Proceedings of the Conference on Remote Sensing for Environmental Monitoring, GIS Applications, and Geology VI, Stockholm, Sweden, 13–14 September 2006. [Google Scholar] [CrossRef]
- Song, C.; Jia, L.; Menenti, M. Retrieving High-Resolution Surface Soil Moisture by Downscaling AMSR-E Brightness Temperature Using MODIS LST and NDVI Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 935–942. [Google Scholar] [CrossRef]
- Sun, D.; Kafatos, M. Note on the NDVI-LST relationship and the use of temperature-related drought indices over North America. Geophys. Res. Lett. 2007, 34, L24406. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Luo, Y.; Li, M.; Yang, K.; Liu, Q.; Li, X. A Taylor Expansion Algorithm for Spatial Downscaling of MODIS Land Surface Temperature. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]










| Site | Imagining Date | Location | Landsat 8 | Sentinel-3 OLCI | Sentinel3 SLSTR | |
|---|---|---|---|---|---|---|
| Path/Row | Overpass Time (UTC/GMT+08:00) | |||||
| 1 | 19 June 2021 | Beijing | 123/32 | 10:53:22 | 10:17:30 | |
| 2 | 3 December 2021 | Guilin | 124/43 | 11:04:26 | 10:52:07 | |
| 3 | 30 May 2021 | Xi’an–Xian Yang | 127/36 | 11:19:33 | 10:36:10 | |
| 4 | 20 November 2021 | Taihu River Basin | 119/38 | 10:31:19 | 10:07:49 | |
| Site | Location | Acquisition Date | Sentinel-3 OLCI | Sentinel3SLSTR |
|---|---|---|---|---|
| Overpass Time (UTC/GMT+08:00) | ||||
| 2 | Guilin | 3 December 2021 (winter) | 10:52:07 | |
| 8 March 2022 (spring) | 10:27:56 | |||
| 6 June 2021 (summer) | 10:57:53 | |||
| 22 October 2020 (fall) | 10:42:49 | |||
| 3 | Xi’an–Xian Yang | 19 February 2021 (winter) | 10:28:37 | |
| 8 May 2021 (spring) | 11:07:44 | |||
| 1 August 2021 (summer) | 11:04:09 | |||
| 10 November 2021 (fall) | 10:45:23 | |||
| Sensor | j = 1 | j = 2 | j = 3 | |
|---|---|---|---|---|
| Landsat 8 TIRS | i = 1 | 0.04019 | 0.02916 | 1.01523 |
| i = 2 | −0.38333 | −1.50294 | 0.20324 | |
| i = 3 | 0.00918 | 1.36072 | −0.27514 |
| Indicator | Model | Site | |||
|---|---|---|---|---|---|
| Beijing | Guilin | Xi’an–Xian Yang | Taihu Rive Basin | ||
| MB/K | D-DisTrad | 1.728 | −0.156 | −0.795 | 0.510 |
| DisTrad | 1.698 | −0.143 | −0.787 | 0.522 | |
| TsHARP | 1.626 | −0.170 | −0.576 | 0.501 | |
| MAE/K | D-DisTrad | 2.189 | 1.067 | 1.633 | 0.898 |
| DisTrad | 2.292 | 1.109 | 1.621 | 0.931 | |
| TsHARP | 2.356 | 1.100 | 1.520 | 0.913 | |
| RMSE/K | D-DisTrad | 2.789 | 1.409 | 2.011 | 1.011 |
| DisTrad | 2.955 | 1.461 | 1.997 | 1.151 | |
| TsHARP | 3.021 | 1.451 | 1.974 | 1.134 | |
| PCC | D-DisTrad | 0.888 | 0.767 | 0.729 | 0.905 |
| DisTrad | 0.858 | 0.750 | 0.731 | 0.878 | |
| TsHARP | 0.837 | 0.746 | 0.702 | 0.892 | |
| D-DisTrad | 0.774 | 0.582 | 0.531 | 0.812 | |
| DisTrad | 0.723 | 0.551 | 0.534 | 0.774 | |
| TsHARP | 0.689 | 0.544 | 0.511 | 0.781 | |
| Indicator | Model | Site | |||
|---|---|---|---|---|---|
| Beijing | Guilin | Xi’an–Xian Yang | Taihu Rive Basin | ||
| MB/K | D-DisTrad | 0.022 | −0.001 | −0.008 | −0.001 |
| DisTrad | 0.013 | 0.005 | −0.005 | 0.005 | |
| TsHARP | −0.074 | −0.019 | 0.210 | −0.007 | |
| MAE/K | D-DisTrad | 0.891 | 0.352 | 0.405 | 0.103 |
| DisTrad | 0.984 | 0.376 | 0.437 | 0.220 | |
| TsHARP | 1.058 | 0.372 | 0.486 | 0.205 | |
| RMSE/K | D-DisTrad | 1.235 | 0.454 | 0.546 | 0.220 |
| DisTrad | 1.410 | 0.513 | 0.589 | 0.380 | |
| TsHARP | 1.448 | 0.514 | 0.642 | 0.379 | |
| PCC | D-DisTrad | 0.952 | 0.974 | 0.972 | 0.994 |
| DisTrad | 0.939 | 0.967 | 0.968 | 0.983 | |
| TsHARP | 0.934 | 0.966 | 0.964 | 0.984 | |
| D-DisTrad | 0.907 | 0.949 | 0.945 | 0.989 | |
| DisTrad | 0.881 | 0.935 | 0.937 | 0.967 | |
| TsHARP | 0.872 | 0.933 | 0.929 | 0.967 | |
| Index | Model | Season | |||
|---|---|---|---|---|---|
| Winter | Spring | Summer | Fall | ||
| MB/K | D-DisTrad | 0.011 | 0.007 | 0.012 | 0.017 |
| DisTrad | 0.019 | 0.013 | 0.015 | 0.017 | |
| TsHARP | 0.006 | 0.068 | 0.095 | 0.017 | |
| MAE/K | D-DisTrad | 0.266 | 0.570 | 0.483 | 0.296 |
| DisTrad | 0.319 | 0.604 | 0.743 | 0.415 | |
| TsHARP | 0.272 | 0.605 | 0.766 | 0.316 | |
| RMSE/K | D-DisTrad | 0.400 | 0.756 | 0.624 | 0.491 |
| DisTrad | 0.471 | 0.792 | 0.924 | 0.625 | |
| TsHARP | 0.408 | 0.806 | 0.975 | 0.503 | |
| PCC | D-DisTrad | 0.960 | 0.955 | 0.977 | 0.949 |
| DisTrad | 0.946 | 0.950 | 0.933 | 0.920 | |
| TsHARP | 0.958 | 0.949 | 0.929 | 0.946 | |
| D-DisTrad | 0.921 | 0.910 | 0.955 | 0.920 | |
| DisTrad | 0.896 | 0.902 | 0.941 | 0.895 | |
| TsHARP | 0.918 | 0.901 | 0.936 | 0.900 | |
| Index | Model | Season | |||
|---|---|---|---|---|---|
| Winter | Spring | Summer | Fall | ||
| MB/K | D-DisTrad | −0.001 | −0.001 | 0.005 | 0.005 |
| DisTrad | 0.005 | 0.001 | 0.005 | 0.005 | |
| TsHARP | −0.019 | −0.016 | −0.013 | 0.003 | |
| MAE/K | D-DisTrad | 0.352 | 0.442 | 0.420 | 0.452 |
| DisTrad | 0.376 | 0.512 | 0.628 | 0.687 | |
| TsHARP | 0.372 | 0.511 | 0.622 | 0.706 | |
| RMSE/K | D-DisTrad | 0.454 | 0.616 | 0.679 | 0.783 |
| DisTrad | 0.513 | 0.720 | 0.995 | 1.005 | |
| TsHARP | 0.514 | 0.738 | 1.016 | 1.059 | |
| PCC | D-DisTrad | 0.974 | 0.942 | 0.938 | 0.964 |
| DisTrad | 0.967 | 0.921 | 0.876 | 0.942 | |
| TsHARP | 0.966 | 0.918 | 0.871 | 0.935 | |
| D-DisTrad | 0.949 | 0.897 | 0.889 | 0.929 | |
| DisTrad | 0.935 | 0.849 | 0.767 | 0.887 | |
| TsHARP | 0.933 | 0.843 | 0.759 | 0.875 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Sui, L.; Zhang, S. Generating Daily Land Surface Temperature Downscaling Data Based on Sentinel-3 Images. Remote Sens. 2022, 14, 5752. https://doi.org/10.3390/rs14225752
Wang Z, Sui L, Zhang S. Generating Daily Land Surface Temperature Downscaling Data Based on Sentinel-3 Images. Remote Sensing. 2022; 14(22):5752. https://doi.org/10.3390/rs14225752
Chicago/Turabian StyleWang, Zhoujin, Lichun Sui, and Shiqi Zhang. 2022. "Generating Daily Land Surface Temperature Downscaling Data Based on Sentinel-3 Images" Remote Sensing 14, no. 22: 5752. https://doi.org/10.3390/rs14225752
APA StyleWang, Z., Sui, L., & Zhang, S. (2022). Generating Daily Land Surface Temperature Downscaling Data Based on Sentinel-3 Images. Remote Sensing, 14(22), 5752. https://doi.org/10.3390/rs14225752