Decadal Changes in Glacier Area, Surface Elevation and Mass Balance for 2000–2020 in the Eastern Tanggula Mountains Using Optical Images and TanDEM-X Radar Data
Abstract
:1. Introduction
2. Study Region
3. Data and Methods
4. Results
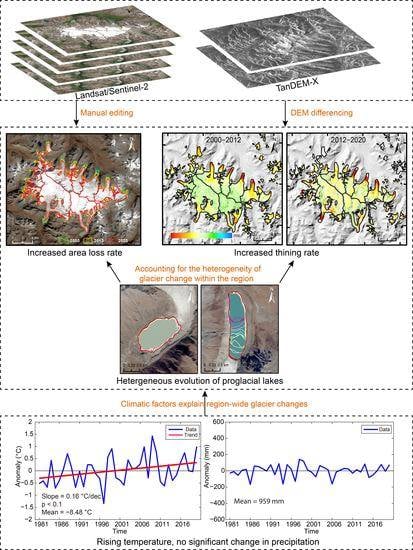
4.1. Glacier Area Change
4.2. Glacier Thickness Change
4.3. Glacier Mass Balance
5. Discussion
5.1. Impact of the Evolution of Proglacial Lake on Glacier Change
5.2. Climate Analysis
5.3. Comparison with Previous Studies
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shean, D.E.; Bhushan, S.; Montesano, P.; Rounce, D.R.; Arendt, A.; Osmanoglu, B. A systematic, regional assessment of high mountain asia glacier mass balance. Front. Earth Sci. 2020, 7, 363. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Li, Z.; Li, J.; Zhao, R.; Ding, X. Glacier mass balance in the qinghai–tibet plateau and its surroundings from the mid-1970s to 2000 based on hexagon kh-9 and srtm dems. Remote Sens. Environ. 2018, 210, 96–112. [Google Scholar] [CrossRef]
- Hugonnet, R.; McNabb, R.; Berthier, E.; Menounos, B.; Nuth, C.; Girod, L.; Farinotti, D.; Huss, M.; Dussaillant, I.; Brun, F.; et al. Accelerated global glacier mass loss in the early twenty-first century. Nature 2021, 592, 726–731. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Bolch, T.; Mukherjee, K.; King, O.; Menounos, B.; Kapitsa, V.; Neckel, N.; Yang, W.; Yao, T. High mountain asian glacier response to climate revealed by multi-temporal satellite observations since the 1960s. Nat. Commun. 2021, 12, 4133. [Google Scholar] [CrossRef]
- Nie, Y.; Sheng, Y.; Liu, Q.; Liu, L.; Liu, S.; Zhang, Y.; Song, C. A regional-scale assessment of himalayan glacial lake changes using satellite observations from 1990 to 2015. Remote Sens. Environ. 2017, 189, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Tsutaki, S.; Fujita, K.; Nuimura, T.; Sakai, A.; Sugiyama, S.; Komori, J.; Tshering, P. Contrasting thinning patterns between lake- and land-terminating glaciers in the bhutanese himalaya. Cryosphere 2019, 13, 2733–2750. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Mayer, C.; Wang, X.; Nie, Y.; Wu, K.; Wei, J.; Liu, S. Interannual flow dynamics driven by frontal retreat of a lake-terminating glacier in the chinese central himalaya. Earth Planet. Sci. Lett. 2020, 546. [Google Scholar] [CrossRef]
- Felikson, D.; Bartholomaus, T.C.; Catania, G.; Korsgaard, N.J.; Kjær, K.H.; Morlighem, M.; Noël, B.P.Y.; Broeke, M.v.d.; Stearns, L.A.; Shroyer, E.L.; et al. Inland thinning on the greenland ice sheet controlled by outlet glacier geometry. Nat. Geosci. 2017, 10, 366–369. [Google Scholar] [CrossRef]
- Zhang, G.; Bolch, T.; Allen, S.; Linsbauer, A.; Chen, W.; Wang, W. Glacial lake evolution and glacier–lake interactions in the poiqu river basin, central himalaya, 1964–2017. J. Glaciol. 2019, 65, 347–365. [Google Scholar] [CrossRef] [Green Version]
- Nie, Y.; Liu, Q.; Wang, J.; Zhang, Y.; Sheng, Y.; Liu, S. An inventory of historical glacial lake outburst floods in the himalayas based on remote sensing observations and geomorphological analysis. Geomorphology 2018, 308, 91–106. [Google Scholar] [CrossRef]
- Zheng, G.; Mergili, M.; Emmer, A.; Allen, S.; Bao, A.; Guo, H.; Stoffel, M. The 2020 glacial lake outburst flood at jinwuco, tibet: Causes, impacts, and implications for hazard and risk assessment. Cryosphere 2021, 15, 3159–3180. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X.; Zheng, D.; Li, Z.; An, B.; Wang, Y.; Jiang, D.; Su, J.; Cao, B. The joint driving effects of climate and weather changes caused the chamoli glacier-rock avalanche in the high altitudes of the india himalaya. Sci. China Earth Sci. 2021, 64, 1909–1921. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.A.; Bierkens, M.F.P.; Lutz, A.F.; Immerzeel, W.W. Impact of a global temperature rise of 1.5 degrees celsius on asia’s glaciers. Nature 2017, 549, 257–260. [Google Scholar] [CrossRef]
- Zheng, G.; Allen, S.K.; Bao, A.; Ballesteros-Cánovas, J.A.; Huss, M.; Zhang, G.; Li, J.; Yuan, Y.; Jiang, L.; Yu, T.; et al. Increasing risk of glacial lake outburst floods from future third pole deglaciation. Nat. Clim. Chang. 2021, 11, 411–417. [Google Scholar] [CrossRef]
- Basnett, S.; Kulkarni, A.V.; Bolch, T. The influence of debris cover and glacial lakes on the recession of glaciers in sikkim himalaya, india. J. Glaciol. 2013, 59, 1035–1046. [Google Scholar] [CrossRef] [Green Version]
- Gardelle, J.; Berthier, E.; Arnaud, Y.; Kääb, A. Region-wide glacier mass balances over the pamir-karakoram-himalaya during 1999–2011. Cryosphere 2013, 7, 1263–1286. [Google Scholar] [CrossRef] [Green Version]
- King, O.; Quincey, D.J.; Carrivick, J.L.; Rowan, A.V. Spatial variability in mass loss of glaciers in the everest region, central himalayas, between 2000 and 2015. Cryosphere 2017, 11, 407–426. [Google Scholar] [CrossRef] [Green Version]
- Ke, L.; Song, C.; Yong, B.; Lei, Y.; Ding, X. Which heterogeneous glacier melting patterns can be robustly observed from space? A multi-scale assessment in southeastern tibetan plateau. Remote Sens. Environ. 2020, 242, 111777. [Google Scholar] [CrossRef]
- King, O.; Dehecq, A.; Quincey, D.; Carrivick, J. Contrasting geometric and dynamic evolution of lake and land-terminating glaciers in the central himalaya. Glob. Planet. Chang. 2018, 167, 46–60. [Google Scholar] [CrossRef]
- King, O.; Bhattacharya, A.; Bhambri, R.; Bolch, T. Glacial lakes exacerbate himalayan glacier mass loss. Sci. Rep. 2019, 9, 18145. [Google Scholar] [CrossRef] [Green Version]
- Maurer, J.M.; Schaefer, J.M.; Rupper, S.; Corley, A. Acceleration of ice loss across the himalayas over the past 40 years. Sci. Adv. 2019, 5, eaav7266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, W.; Yao, T.; Zhang, G.; Li, S.; Zheng, G. Accelerated glacier mass loss in the largest river and lake source regions of the tibetan plateau and its links with local water balance over 1976–2017. J. Glaciol. 2021, 67, 577–591. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, L.; Zhang, Z.; Wang, H.; Ding, X. Recent accelerating glacier mass loss of the geladandong mountain, inner tibetan plateau, estimated from ziyuan-3 and tandem-x measurements. Remote Sens. 2020, 12, 472. [Google Scholar] [CrossRef] [Green Version]
- Ren, S.; Menenti, M.; Jia, L.; Zhang, J.; Zhang, J.; Li, X. Glacier mass balance in the nyainqentanglha mountains between 2000 and 2017 retrieved from ziyuan-3 stereo images and the srtm dem. Remote Sens. 2020, 12, 864. [Google Scholar] [CrossRef] [Green Version]
- Neckel, N.; Braun, A.; Kropáček, J.; Hochschild, V. Recent mass balance of the purogangri ice cap, central tibetan plateau, by means of differential x-band sar interferometry. Cryosphere 2013, 7, 1623–1633. [Google Scholar] [CrossRef] [Green Version]
- Neelmeijer, J.; Motagh, M.; Bookhagen, B. High-resolution digital elevation models from single-pass tandem-x interferometry over mountainous regions: A case study of inylchek glacier, central asia. ISPRS J. Photogramm. Remote Sens. 2017, 130, 108–121. [Google Scholar] [CrossRef] [Green Version]
- Leinss, S.; Bernhard, P. Tandem-x:Deriving insar height changes and velocity dynamics of great aletsch glacier. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4798–4815. [Google Scholar] [CrossRef]
- Rossi, C.; Minet, C.; Fritz, T.; Eineder, M.; Bamler, R. Temporal monitoring of subglacial volcanoes with tandem-x—Application to the 2014–2015 eruption within the bárðarbunga volcanic system, iceland. Remote Sens. Environ. 2016, 181, 186–197. [Google Scholar] [CrossRef] [Green Version]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef] [Green Version]
- Gardelle, J.; Berthier, E.; Arnaud, Y. Impact of resolution and radar penetration on glacier elevation changes computed from dem differencing. J. Glaciol. 2012, 58, 419–422. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Jiang, L.; Liu, L.; Wang, H. Regional and altitude-dependent estimate of the srtm c/x-band radar penetration difference on high mountain asia glaciers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4244–4253. [Google Scholar] [CrossRef]
- Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 2013, 7, 877–887. [Google Scholar] [CrossRef] [Green Version]
- Cao, B.; Gruber, S.; Zheng, D.; Li, X. The era5-land soil temperature bias in permafrost regions. Cryosphere 2020, 14, 2581–2595. [Google Scholar] [CrossRef]
- Paul, F.; Bolch, T.; Briggs, K.; Kääb, A.; McMillan, M.; McNabb, R.; Nagler, T.; Nuth, C.; Rastner, P.; Strozzi, T.; et al. Error sources and guidelines for quality assessment of glacier area, elevation change, and velocity products derived from satellite data in the glaciers_cci project. Remote Sens. Environ. 2017, 203, 256–275. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Hu, J.; Li, Z.; Li, J.; Zhao, R.; Ding, X. Quantifying glacier mass change and its contribution to lake growths in central kunlun during 2000–2015 from multi-source remote sensing data. J. Hydrol. 2019, 570, 38–50. [Google Scholar] [CrossRef]
- Rolstad, C.; Haug, T.; Denby, B. Spatially integrated geodetic glacier mass balance and its uncertainty based on geostatistical analysis: Application to the western svartisen ice cap, norway. J. Glaciol. 2009, 55, 666–680. [Google Scholar] [CrossRef] [Green Version]
- Chen, A.a.; Wang, N.; Li, Z.; Wu, Y.; Zhang, W.; Guo, Z. Region-wide glacier mass budgets for the tanggula mountains between ∼1969 and ∼2015 derived from remote sensing data. Arct. Antarct. Alp. Res. 2017, 49, 551–568. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Lin, H. Recent decadal glacier mass balances over the western nyainqentanglha mountains and the increase in their melting contribution to nam co lake measured by differential bistatic sar interferometry. Glob. Planet. Chang. 2017, 149, 177–190. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Zhang, G.; Chen, W.; Xu, F. Response of glacial lakes to glacier and climate changes in the western nyainqentanglha range. Sci. Total Environ. 2020, 735, 139607. [Google Scholar] [CrossRef]
- Wu, K.; Liu, S.; Jiang, Z.; Xu, J.; Wei, J. Glacier mass balance over the central nyainqentanglha range during recent decades derived from remote-sensing data. J. Glaciol. 2019, 65, 422–439. [Google Scholar] [CrossRef] [Green Version]











| Sensor | Path/Row | Date of Acquisition | Spatial Resolution | Purpose |
|---|---|---|---|---|
| SRTM C-band DEM | 2000/02 | 30.0 m 90.0 m | Reference DEM Elevation change | |
| SRTM X-band DEM | 2000/02 | 25 m | Penetration depth estimation | |
| TanDEM-X | 2012/11/14 2020/01/02 | ~2.0 m | Elevation change | |
| Landsat-5 | 136/38 | 2000/07/22 2001/07/09 | 30 m | Glacier boundaries |
| Landsat-8 | 136/38 | 2013/09/28 2014/11/18 | 15 m | Glacier boundaries |
| Sentinel-2 | 2020/10/30 | 10 m | Glacier boundaries | |
| ERA5-Land | 1981–2020 | 0.1° × 0.1° | Climate analysis |
| Glacier Name | Glacier Area (km2) | Area Change (km2) | Rate of Area Change (km2 a−1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2000 | 2013 | 2020 | 2000–2013 | 2013–2000 | 2000–2020 | 2000–2013 | 2013–2000 | 2000–2020 | |
| G59 | 4.61 ± 0.29 | 4.32 ± 0.15 | 4.10 ± 0.10 | −0.29 ± 0.33 | −0.22 ± 0.17 | −0.51 ± 0.31 | −0.02 ± 0.02 | −0.03 ± 0.02 | −0.02 ± 0.01 |
| G88 | 1.28 ± 0.14 | 1.10 ± 0.07 | 1.07 ± 0.04 | −0.18 ± 0.14 | −0.03 ± 0.08 | −0.21 ± 0.14 | −0.01 ± 0.01 | 0.00 ± 0.01 | −0.01 ± 0.01 |
| G71 * | 2.33 ± 0.27 | 2.30 ± 0.14 | 2.16 ± 0.09 | −0.03 ± 0.30 | −0.14 ± 0.16 | −0.17 ± 0.28 | 0.00 ± 0.02 | −0.02 ± 0.02 | −0.01 ± 0.01 |
| G22 * | 2.17 ± 0.27 | 2.06 ± 0.14 | 1.89 ± 0.09 | −0.11 ± 0.30 | −0.17 ± 0.16 | −0.28 ± 0.28 | −0.01 ± 0.02 | −0.02 ± 0.02 | −0.01 ± 0.01 |
| G21 * | 5.39 ± 0.47 | 5.21 ± 0.23 | 4.89 ± 0.16 | −0.18 ± 0.51 | −0.32 ± 0.27 | −0.50 ± 0.49 | −0.01 ± 0.04 | −0.04 ± 0.04 | −0.02 ± 0.02 |
| ZGMN * | 15.81 ± 0.77 | 15.50 ± 0.39 | 15.02 ± 0.26 | −0.31 ± 0.86 | −0.48 ± 0.46 | −0.79 ± 0.81 | −0.03 ± 0.06 | −0.06 ± 0.06 | −0.04 ± 0.04 |
| West Beijia * | 8.59 ± 0.57 | 8.20 ± 0.28 | 7.85 ± 0.19 | −0.39 ± 0.63 | −0.35 ± 0.34 | −0.74 ± 0.59 | −0.03 ± 0.04 | −0.05 ± 0.05 | −0.04 ± 0.03 |
| Beijia * | 13.58 ± 0.57 | 13.13 ± 0.28 | 12.73 ± 0.19 | −0.45 ± 0.63 | −0.40 ± 0.34 | −0.85 ± 0.59 | −0.04 ± 0.04 | −0.05 ± 0.05 | −0.04 ± 0.03 |
| East Beijia * | 10.48 ± 0.60 | 10.15 ± 0.30 | 9.55 ± 0.20 | −0.33 ± 0.66 | −0.60 ± 0.35 | −0.93 ± 0.62 | −0.02 ± 0.05 | −0.09 ± 0.05 | −0.05 ± 0.03 |
| Zuxuehui * | 35.87 ± 1.23 | 35.15 ± 0.62 | 35.00 ± 0.41 | −0.72 ± 1.37 | −0.15 ± 0.73 | −0.87 ± 1.29 | −0.05 ± 0.10 | −0.02 ± 0.10 | −0.04 ± 0.06 |
| Poge * | 21.11 ± 1.20 | 20.91 ± 0.60 | 20.64 ± 0.40 | −0.20 ± 1.33 | −0.27 ± 0.71 | −0.47 ± 1.25 | −0.01 ± 0.10 | −0.04 ± 0.10 | −0.02 ± 0.06 |
| All glaciers | 143.23 ± 9.69 | 138.83 ± 4.73 | 132.35 ± 3.17 | −4.40 ± 10.78 | −6.48 ± 5.69 | −10.88 ± 10.19 | −0.34 ± 0.83 | −0.93 ± 0.81 | −0.54 ± 0.51 |
| Glacier Name | ELA (m) | 2000–2012 | 2012–2020 | 2000–2020 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Thickness Change Rate (m a−1) | Mass Balance (w.e. a−1) | Thickness Change Rate (m a−1) | Mass Balance (w.e. a−1) | Thickness Change Rate (m a−1) | Mass Balance (w.e. a−1) | |||||
| Acc. Zone | Abl. Zone | Acc. Zone | Abl. Zone | Acc. Zone | Abl. | |||||
| G59 | 5400 | −0.02 ± 0.44 | −0.51 ± 0.38 | −0.22 ± 0.21 | −0.24 ± 0.60 | −0.75 ± 0.48 | −0.40 ± 0.24 | 0.01 ± 0.30 | −0.53 ± 0.27 | −0.21 ± 0.14 |
| G61 | 5294 | −0.39 ± 0.71 | −0.83 ± 0.61 | −0.56 ± 0.34 | −0.15 ± 0.88 | −1.01 ± 0.73 | −0.54 ± 0.36 | −0.41 ± 0.53 | −0.93 ± 0.43 | −0.58 ± 0.23 |
| G88 | 5364 | −0.27 ± 0.79 | −1.10 ± 0.74 | −0.65 ± 0.35 | −0.37 ± 0.88 | −0.88 ± 0.86 | −0.59 ± 0.36 | −0.21 ± 0.52 | −1.01 ± 0.49 | −0.58 ± 0.23 |
| G71 * | 5383 | 0.10 ± 0.80 | −0.58 ± 0.55 | −0.20 ± 0.23 | −0.02 ± 0.88 | −0.79 ± 0.65 | −0.33 ± 0.25 | 0.27 ± 0.54 | −0.57 ± 0.36 | −0.12 ± 0.15 |
| ZGMN * | 5560 | 0.18 ± 0.23 | −0.70 ± 0.20 | −0.21 ± 0.12 | −0.14 ± 0.28 | −0.55 ± 0.25 | −0.29 ± 0.14 | 0.10 ± 0.13 | −0.54 ± 0.14 | −0.18 ± 0.08 |
| W-Beijia * | 5587 | 0.29 ± 0.28 | −0.63 ± 0.26 | −0.14 ± 0.15 | −0.21 ± 0.34 | −1.13 ± 0.32 | −0.53 ± 0.18 | 0.12 ± 0.19 | −0.64 ± 0.18 | −0.22 ± 0.10 |
| Beijia * | 5593 | 0.40 ± 0.24 | −0.57 ± 0.22 | −0.07 ± 0.13 | −0.15 ± 0.28 | −0.75 ± 0.26 | −0.41 ± 0.15 | 0.20 ± 0.16 | −0.44 ± 0.15 | −0.11 ± 0.08 |
| E-Beijia * | 5345 | −0.01 ± 0.27 | −1.12 ± 0.25 | −0.48 ± 0.16 | −0.17 ± 0.34 | −1.41 ± 0.29 | −0.67 ± 0.18 | −0.01 ± 0.19 | −1.24 ± 0.16 | −0.52 ± 0.12 |
| G21 * | 5615 | 0.30 ± 0.45 | −0.61 ± 0.38 | −0.13 ± 0.20 | −0.41 ± 0.69 | −1.22 ± 0.48 | −0.66 ± 0.23 | −0.10 ± 0.29 | −0.80 ± 0.25 | −0.39 ± 0.14 |
| G22 * | 5486 | 0.30 ± 0.79 | −0.20 ± 0.62 | 0.10 ± 0.21 | −0.48 ± 0.88 | −1.77 ± 0.75 | −0.91 ± 0.25 | −0.16 ± 0.50 | −0.73 ± 0.40 | −0.35 ± 0.15 |
| Zucxuehui * | 5726 | 0.33 ± 0.14 | −0.16 ± 0.14 | 0.07 ± 0.08 | −0.27 ± 0.18 | −0.76 ± 0.18 | −0.42 ± 0.10 | 0.09 ± 0.09 | −0.34 ± 0.09 | −0.10 ± 0.05 |
| Poge * | 5890 | 0.40 ± 0.18 | −0.35 ± 0.20 | 0.05 ± 0.10 | −0.21 ± 0.22 | −0.45 ± 0.23 | −0.25 ± 0.12 | 0.18 ± 0.12 | −0.26 ± 0.13 | −0.01 ± 0.06 |
| Lake-terminating | 5576 | 0.33 ± 0.08 | −0.57 ± 0.08 | −0.08 ± 0.05 | −0.21 ± 0.10 | −0.86 ± 0.10 | −0.43 ± 0.07 | 0.12 ± 0.05 | −0.57 ± 0.05 | −0.17 ± 0.04 |
| Land-terminating | 5390 | −0.18 ± 0.15 | −0.70 ± 0.11 | −0.38 ± 0.08 | −0.29 ± 0.27 | −0.91 ± 0.17 | −0.54 ± 0.10 | −0.19 ± 0.13 | −0.73 ± 0.10 | −0.42 ± 0.07 |
| All glaciers | 5400 | 0.17 ± 0.06 | −0.73 ± 0.07 | −0.16 ± 0.04 | −0.23 ± 0.09 | −0.99 ± 0.10 | −0.45 ± 0.07 | 0.06 ± 0.04 | −0.76 ± 0.05 | −0.23 ± 0.04 |
| Region | Data | Periods | Glacier Mass Balance (m w.e. a−1) | Sources |
|---|---|---|---|---|
| Western Tanggula (Geladandong) | SRTM DEM, TanDEM-X, ZY-3 | 2000–2012 2012–2018 2000–2018 | –0.11 ± 0.03 –0.47±0.09 –0.24 ± 0.07 | Liu et al. [23] |
| SRTM DEM, TanDEM-X | 2000–2011 2011–2017 2000–2017 | –0.24 ± 0.12 –0.41 ± 0.09 –0.30 ± 0.08 | Chen et al. [22] | |
| Western Nyainqentanglha | SRTM DEM, TanDEM-X | 2000–2013 | −0.24 ± 0.13 | Li et al. [38] |
| SRTM DEM, TanDEM-X | 2000–2014 | –0.25 ± 0.08 | Luo et al. [39] | |
| SRTM DEM, ZY-3 | 2000–2013 2013–2017 2000–2017 | −0.22 ± 0.23 −0.43 ± 0.06 −0.30 ± 0.19 | Ren et al. [24] | |
| Eastern Nyainqentanglha (Yigong Zangbo) | SRTM DEM, TanDEM-X | 2000–2013 | −0.60 ± 0.20 (all) | Wu et al. [40] |
| SRTM DEM, TanDEM-X DEM, AW3D | 2000–2010s | −0.66 ± 0.19 (all) −0.50 ± 0.32 (land) −0.89 ± 0.36 (lake) | Ke et al. [18] | |
| Himalaya | SRTM DEM HMA DEM | 2000–2015 | –0.39 ± 0.12 (all) –0.37 ± 0.12 (land) –0.55 ± 0.12 (lake) | King et al. [20] |
| ASTER | 2000–2016 | –0.43 ± 0.14 (all) –0.41 ± 0.08 (land) –0.56 ± 0.08 (lake) | Maurer et al. [21] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Li, X.; Zheng, D.; Zhang, X.; Wang, Y.; Ren, S.; Guo, Y. Decadal Changes in Glacier Area, Surface Elevation and Mass Balance for 2000–2020 in the Eastern Tanggula Mountains Using Optical Images and TanDEM-X Radar Data. Remote Sens. 2022, 14, 506. https://doi.org/10.3390/rs14030506
Zhou Y, Li X, Zheng D, Zhang X, Wang Y, Ren S, Guo Y. Decadal Changes in Glacier Area, Surface Elevation and Mass Balance for 2000–2020 in the Eastern Tanggula Mountains Using Optical Images and TanDEM-X Radar Data. Remote Sensing. 2022; 14(3):506. https://doi.org/10.3390/rs14030506
Chicago/Turabian StyleZhou, Yushan, Xin Li, Donghai Zheng, Xiaolong Zhang, Yingzheng Wang, Shanshan Ren, and Yanlong Guo. 2022. "Decadal Changes in Glacier Area, Surface Elevation and Mass Balance for 2000–2020 in the Eastern Tanggula Mountains Using Optical Images and TanDEM-X Radar Data" Remote Sensing 14, no. 3: 506. https://doi.org/10.3390/rs14030506
APA StyleZhou, Y., Li, X., Zheng, D., Zhang, X., Wang, Y., Ren, S., & Guo, Y. (2022). Decadal Changes in Glacier Area, Surface Elevation and Mass Balance for 2000–2020 in the Eastern Tanggula Mountains Using Optical Images and TanDEM-X Radar Data. Remote Sensing, 14(3), 506. https://doi.org/10.3390/rs14030506