Combining Sample Plot Stratification and Machine Learning Algorithms to Improve Forest Aboveground Carbon Density Estimation in Northeast China Using Airborne LiDAR Data
Abstract
:1. Introduction
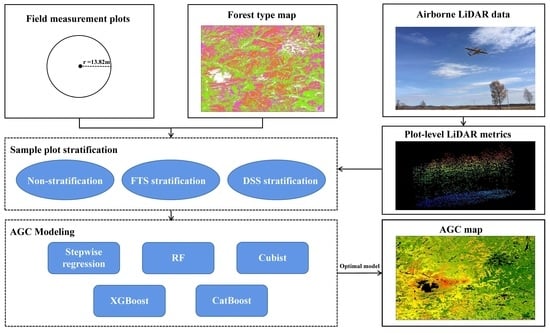
2. Materials and Methods
2.1. Study Area
2.2. Data Source and Preprocessing
2.2.1. Field Measurements Data and Forest AGC Calculation
2.2.2. Design of Sample Plot Stratification
2.2.3. Airborne Laser Scanning Data
2.3. Methods
2.3.1. Model Variables Extraction and Selection
2.3.2. Modeling Algorithms
2.3.3. Hyperparameter Optimization in Machine Learning Algorithm
2.3.4. Statistical Analysis
2.3.5. Model Validation
3. Results
3.1. Comparative Analysis of Forest AGC Estimation Results
3.1.1. Forest AGC Estimation Results Based on FTS
3.1.2. Aboveground Carbon Density Estimation Results Based on DSS
3.1.3. Comparative Analysis of Forest AGC Estimation Results Based on FTS and DSS
3.2. Variable Importance Analysis
4. Discussion
4.1. Variables Selection in Forest AGC Estimation
4.2. The Role of Stratification in Forest AGC Estimation
4.3. FTS versus DSS
4.4. Machine-Learning Algorithms for Forest AGC Estimation
4.5. Species-Level Forest AGC Estimation
4.6. Uncertainty Analysis and Limitations
5. Conclusions
- (1)
- The ANOVA result showed that the stratification method had a more important effect on forest AGC estimation than the regression algorithm. Both FTS and DSS were effective in improving the estimation accuracy of forest AGC compared to non-stratified models, demonstrating the positive role of stratification in forest AGC estimation. Compared to the non-stratified models, the estimation accuracy of forest AGC was significantly improved in coniferous species, while marginal improvement was observed in the broadleaf species.
- (2)
- Compared with FTS, models based on DSS achieved greater improvements, indicating that DSS is a better stratification estimation method for forest AGC.
- (3)
- Regardless of the stratification method used, of the five algorithms, the four non-parametric ML algorithms outperformed parametric stepwise regression, with the CatBoost algorithm obtaining the best estimation performance, followed by XGBoost, RF, Cubist and stepwise regression.
- (4)
- The most important LiDAR metrics for forest AGC estimation were the height percentiles and the canopy relief ratio.
- (5)
- The CatBoost models based on DSS achieved the highest estimation accuracy, with R2 = 0.8232, RMSE = 5.2421, RRMSE = 20.5680, MAE = 4.0169 and Bias = 0.4493. The estimation values of the best forest AGC estimation model for the eight dominant species ranged from 21.36 to 37.72 Mg/ha, with the Poplar having the highest forest AGC and the White Birch having the lowest.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Six, J.; Callewaert, P.; Lenders, S.; De Gryze, S.; Morris, S.J.; Gregorich, E.G.; Paul, E.A.; Paustian, K. Measuring and Understanding Carbon Storage in Afforested Soils by Physical Fractionation. Soil Sci. Soc. Am. J. 2007, 66, 1981–1987. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.; Ge, J. Valued Forest Carbon Sinks: How Much Emissions Abatement Costs Could Be Reduced in China. J. Clean. Prod. 2019, 224, 455–464. [Google Scholar] [CrossRef]
- Santini, N.S.; Adame, M.F.; Nolan, R.H.; Miquelajauregui, Y.; Pinero, D.; Mastretta-Yanes, A.; Cuervo-Robayo, A.P.; Eamus, D. Storage of Organic Carbon in the Soils of Mexican Temperate Forests. For. Ecol. Manag. 2019, 446, 115–125. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Danson, F.M. Estimating Biomass Carbon Stocks for a Mediterranean Forest in Central Spain Using LiDAR Height and Intensity Data. Remote Sens. Environ. 2010, 114, 816–830. [Google Scholar] [CrossRef]
- Kuuluvainen, T.; Gauthier, S. Young and Old Forest in the Boreal: Critical Stages of Ecosystem Dynamics and Management under Global Change. For. Ecosyst. 2018, 5, 26. [Google Scholar] [CrossRef]
- Zhao, M.; Yang, J.; Zhao, N.; Liu, Y.; Wang, Y.; Wilson, J.P.; Yue, T. Estimation of China’s Forest Stand Biomass Carbon Sequestration Based on the Continuous Biomass Expansion Factor Model and Seven Forest Inventories from 1977 to 2013. For. Ecol. Manag. 2019, 448, 528–534. [Google Scholar] [CrossRef]
- Fang, J.; Guo, Z.; Hu, H.; Kato, T.; Muraoka, H.; Son, Y. Forest Biomass Carbon Sinks in East Asia, with Special Reference to the Relative Contributions of Forest Expansion and Forest Growth. Glob. Chang. Biol. 2014, 20, 2019–2030. [Google Scholar] [CrossRef] [PubMed]
- Mitchard, E.T.A. The Tropical Forest Carbon Cycle and Climate Change. Nature 2018, 559, 527–534. [Google Scholar] [CrossRef] [PubMed]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS Mission: Mapping Global Forest Biomass to Better Understand the Terrestrial Carbon Cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A Survey of Remote Sensing-Based Aboveground Biomass Estimation Methods in Forest Ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Lin, C.; Thomson, G.; Popescu, S.C. An IPCC-Compliant Technique for Forest Carbon Stock Assessment Using Airborne LiDAR-Derived Tree Metrics and Competition Index. Remote Sens. 2016, 8, 528. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Ramirez, C.; Kennedy, K.; Mallory, J. A New Approach to Extrapolate Forest Attributes from Field Inventory with Satellite and Auxiliary Data Sets. For. Sci. 2017, 63, 232–240. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zan, Q.; Yang, Q.; Zhu, D.; Chen, Y.; Yu, S. Remote Estimation of Mangrove Aboveground Carbon Stock at the Species Level Using a Low-Cost Unmanned Aerial Vehicle System. Remote Sens. 2019, 11, 1018. [Google Scholar] [CrossRef] [Green Version]
- Xie, B.; Cao, C.; Xu, M.; Bashir, B.; Singh, R.P.; Huang, Z.; Lin, X. Regional Forest Volume Estimation by Expanding LiDAR Samples Using Multi-Sensor Satellite Data. Remote Sens. 2020, 12, 360. [Google Scholar] [CrossRef] [Green Version]
- Lu, D. The Potential and Challenge of Remote Sensing-based Biomass Estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved Allometric Models to Estimate the Aboveground Biomass of Tropical Trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A Meta-Analysis of Terrestrial Aboveground Biomass Estimation Using Lidar Remote Sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Brovkina, O.; Novotny, J.; Cienciala, E.; Zemek, F.; Russ, R. Mapping Forest Aboveground Biomass Using Airborne Hyperspectral and LiDAR Data in the Mountainous Conditions of Central Europe. Ecol. Eng. 2017, 100, 219–230. [Google Scholar] [CrossRef]
- Cao, L.; Pan, J.; Li, R.; Li, J.; Li, Z. Integrating Airborne LiDAR and Optical Data to Estimate Forest Aboveground Biomass in Arid and Semi-Arid Regions of China. Remote Sens. 2018, 10, 532. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Li, G.; Lu, D.; Chen, E.; Wei, X. Stratification-Based Forest Aboveground Biomass Estimation in a Subtropical Region Using Airborne Lidar Data. Remote Sens. 2020, 12, 1101. [Google Scholar] [CrossRef] [Green Version]
- Poorazimy, M.; Shataee, S.; McRoberts, R.E.; Mohammadi, J. Integrating Airborne Laser Scanning Data, Space-Borne Radar Data and Digital Aerial Imagery to Estimate Aboveground Carbon Stock in Hyrcanian Forests, Iran. Remote Sens. Environ. 2020, 240, 111669. [Google Scholar] [CrossRef]
- Chan, E.P.Y.; Fung, T.; Wong, F.K.K. Estimating Above-Ground Biomass of Subtropical Forest Using Airborne LiDAR in Hong Kong. Sci. Rep. 2021, 11, 1751. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. Forest Biomass Estimation from Airborne LiDAR Data Using Machine Learning Approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Li, M.; Im, J.; Quackenbush, L.J.; Liu, T. Forest Biomass and Carbon Stock Quantification Using Airborne LiDAR Data: A Case Study Over Huntington Wildlife Forest in the Adirondack Park. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3143–3156. [Google Scholar] [CrossRef]
- John, R.; Chen, J.; Giannico, V.; Park, H.; Xiao, J.; Shirkey, G.; Ouyang, Z.; Shao, C.; Lafortezza, R.; Qi, J. Grassland Canopy Cover and Aboveground Biomass in Mongolia and Inner Mongolia: Spatiotemporal Estimates and Controlling Factors. Remote Sens. Environ. 2018, 213, 34–48. [Google Scholar] [CrossRef]
- Huang, W.; Dolan, K.; Swatantran, A.; Johnson, K.; Tang, H.; O’Neil-Dunne, J.; Dubayah, R.; Hurtt, G. High-Resolution Mapping of Aboveground Biomass for Forest Carbon Monitoring System in the Tri-State Region of Maryland, Pennsylvania and Delaware, USA. Environ. Res. Lett. 2019, 14, 095002. [Google Scholar] [CrossRef] [Green Version]
- Dos Reis, A.A.; Werner, J.P.S.; Silva, B.C.; Figueiredo, G.K.D.A.; Antunes, J.F.G.; Esquerdo, J.C.D.M.; Coutinho, A.C.; Lamparelli, R.A.C.; Rocha, J.V.; Magalhães, P.S.G. Monitoring Pasture Aboveground Biomass and Canopy Height in an Integrated Crop–Livestock System Using Textural Information from PlanetScope Imagery. Remote Sens. 2020, 12, 2534. [Google Scholar] [CrossRef]
- Sun, H.; He, J.; Chen, Y.; Zhao, B. Space-Time Sea Surface PCO2 Estimation in the North Atlantic Based on CatBoost. Remote Sens. 2021, 13, 2805. [Google Scholar] [CrossRef]
- Ahirwal, J.; Nath, A.; Brahma, B.; Deb, S.; Sahoo, U.K.; Nath, A.J. Patterns and Driving Factors of Biomass Carbon and Soil Organic Carbon Stock in the Indian Himalayan Region. Sci. Total Environ. 2021, 770, 145292. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Gobakken, T.; Næsset, E. Post-Stratified Estimation of Forest Area and Growing Stock Volume Using Lidar-Based Stratifications. Remote Sens. Environ. 2012, 125, 157–166. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest Aboveground Biomass Estimation in Zhejiang Province Using the Integration of Landsat TM and ALOS PALSAR Data. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Shao, G.; Shao, G.; Gallion, J.; Saunders, M.R.; Frankenberger, J.R.; Fei, S. Improving Lidar-Based Aboveground Biomass Estimation of Temperate Hardwood Forests with Varying Site Productivity. Remote Sens. Environ. 2018, 204, 872–882. [Google Scholar] [CrossRef]
- Silveira, E.M.O.; Espírito Santo, F.D.; Wulder, M.A.; Acerbi Júnior, F.W.; Carvalho, M.C.; Mello, C.R.; Mello, J.M.; Shimabukuro, Y.E.; Terra, M.C.N.S.; Carvalho, L.M.T.; et al. Pre-Stratified Modelling plus Residuals Kriging Reduces the Uncertainty of Aboveground Biomass Estimation and Spatial Distribution in Heterogeneous Savannas and Forest Environments. For. Ecol. Manag. 2019, 445, 96–109. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative Analysis of Modeling Algorithms for Forest Aboveground Biomass Estimation in a Subtropical Region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef] [Green Version]
- Tonolli, S.; Dalponte, M.; Neteler, M.; Rodeghiero, M.; Vescovo, L.; Gianelle, D. Fusion of Airborne LiDAR and Satellite Multispectral Data for the Estimation of Timber Volume in the Southern Alps. Remote Sens. Environ. 2011, 115, 2486–2498. [Google Scholar] [CrossRef]
- Kulawardhana, R.W.; Popescu, S.C.; Feagin, R.A. Fusion of Lidar and Multispectral Data to Quantify Salt Marsh Carbon Stocks. Remote Sens. Environ. 2014, 154, 345–357. [Google Scholar] [CrossRef]
- Latifi, H.; Fassnacht, F.E.; Hartig, F.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Stratified Aboveground Forest Biomass Estimation by Remote Sensing Data. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 229–241. [Google Scholar] [CrossRef]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in Forest Biomass Carbon Storage in China Between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, H.; Zhou, G.; Zhang, Q.; Tao, J.; Zhang, Y.; Lin, J. Aboveground Mangrove Biomass Estimation in Beibu Gulf Using Machine Learning and UAV Remote Sensing. Sci. Total Environ. 2021, 781, 146816. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, S.; Sun, G. Forest Biomass Mapping of Northeastern China Using GLAS and MODIS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 140–152. [Google Scholar] [CrossRef]
- Fu, Y.; He, H.S.; Hawbaker, T.J.; Henne, P.D.; Zhu, Z.; Larsen, D.R. Evaluating k-Nearest Neighbor (kNN) Imputation Models for Species-Level Aboveground Forest Biomass Mapping in Northeast China. Remote Sens. 2019, 11, 2005. [Google Scholar] [CrossRef] [Green Version]
- Vaglio Laurin, G.; Puletti, N.; Hawthorne, W.; Liesenberg, V.; Corona, P.; Papale, D.; Chen, Q.; Valentini, R. Discrimination of Tropical Forest Types, Dominant Species, and Mapping of Functional Guilds by Hyperspectral and Simulated Multispectral Sentinel-2 Data. Remote Sens. Environ. 2016, 176, 163–176. [Google Scholar] [CrossRef] [Green Version]
- Jia, W. Forest Biomass and Carbon Stock of Each Stand Type in the Northeast Forest Region; Heilongjiang Science and Technology Press: Harbin, China, 2015. [Google Scholar]
- LY/T 2654-2016; Tree Biomass Models and Related Parameters to Carbon. National Forestry and Grassland Administration of China: Beijing, China, 2016.
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved Progressive TIN Densification Filtering Algorithm for Airborne LiDAR Data in Forested Areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef] [Green Version]
- Axelsson, P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models. Int. Arch. Photogramm. Remote Sens. 2000, 33, 110–117. [Google Scholar]
- Knapp, N.; Fischer, R.; Huth, A. Linking Lidar and Forest Modeling to Assess Biomass Estimation across Scales and Disturbance States. Remote Sens. Environ. 2018, 205, 199–209. [Google Scholar] [CrossRef]
- de Oliveira, C.P.; Caraciolo Ferreira, R.L.; Aleixo da Silva, J.A.; de Lima, R.B.; Silva, E.A.; da Silva, A.F.; Silva de Lucena, J.D.; Tavares dos Santos, N.A.; Correa Lopes, I.J.; de Lima Pessoa, M.M.; et al. Modeling and Spatialization of Biomass and Carbon Stock Using LiDAR Metrics in Tropical Dry Forest, Brazil. Forests 2021, 12, 473. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Pan, F.; Qian, M.; Peng, D.; Nie, S.; Qin, H.; Lin, Y. Retrieving Aboveground Biomass of Wetland Phragmites australis (Common Reed) Using a Combination of Airborne Discrete-Return LiDAR and Hyperspectral Data. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 107–117. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Liu, J.; Su, Y.; Guo, Q.; Qiu, P.; Wu, X. Estimating Aboveground Biomass of the Mangrove Forests on Northeast Hainan Island in China Using an Upscaling Method from Field Plots, UAV-LiDAR Data and Sentinel-2 Imagery. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101986. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Sun, G.; Ranson, K.J.; Guo, Z.; Zhang, Z.; Montesano, P.; Kimes, D. Forest Biomass Mapping from Lidar and Radar Synergies. Remote Sens. Environ. 2011, 115, 2906–2916. [Google Scholar] [CrossRef] [Green Version]
- Kronseder, K.; Ballhorn, U.; Boehm, V.; Siegert, F. Above Ground Biomass Estimation across Forest Types at Different Degradation Levels in Central Kalimantan Using LiDAR Data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 37–48. [Google Scholar] [CrossRef]
- Ku, N.-W.; Popescu, S.C. A Comparison of Multiple Methods for Mapping Local-Scale Mesquite Tree Aboveground Biomass with Remotely Sensed Data. Biomass Bioenergy 2019, 122, 270–279. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zeng, W.; Zhou, H. Evaluation of CatBoost Method for Prediction of Reference Evapotranspiration in Humid Regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- de Almeida, C.T.; Galvão, L.S.; Aragão, L.E.D.O.C.E.; Ometto, J.P.H.B.; Jacon, A.D.; Pereira, F.R.D.S.; Sato, L.Y.; Lopes, A.P.; Graça, P.M.L.D.A.; Silva, C.V.D.J.; et al. Combining LiDAR and Hyperspectral Data for Aboveground Biomass Modeling in the Brazilian Amazon Using Different Regression Algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest Aboveground Biomass Estimation Using Landsat 8 and Sentinel-1A Data with Machine Learning Algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. arXiv 2019, arXiv:1706.09516. [Google Scholar]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for Big Data: An Interdisciplinary Review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- de Souza Pereira, F.R.; Kampel, M.; Gomes Soares, M.L.; Duque Estrada, G.C.; Bentz, C.; Vincent, G. Reducing Uncertainty in Mapping of Mangrove Aboveground Biomass Using Airborne Discrete Return Lidar Data. Remote Sens. 2018, 10, 637. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Shen, X.; Cao, L.; Wang, G.; Cao, F. Estimating Forest Structural Attributes Using UAV-LiDAR Data in Ginkgo Plantations. ISPRS J. Photogramm. Remote Sens. 2018, 146, 465–482. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, T.; Skidmore, A.K.; Heurich, M. Important LiDAR Metrics for Discriminating Forest Tree Species in Central Europe. ISPRS J. Photogramm. Remote Sens. 2018, 137, 163–174. [Google Scholar] [CrossRef]
- Kashani, A.G.; Olsen, M.J.; Parrish, C.E.; Wilson, N. A Review of LIDAR Radiometric Processing: From Ad Hoc Intensity Correction to Rigorous Radiometric Calibration. Sensors 2015, 15, 28099–28128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoefle, B.; Pfeifer, N. Correction of Laser Scanning Intensity Data: Data and Model-Driven Approaches. ISPRS J. Photogramm. Remote Sens. 2007, 62, 415–433. [Google Scholar] [CrossRef]
- Javier Mesas-Carrascosa, F.; Luisa Castillejo-Gonzalez, I.; Sanchez de la Orden, M.; Garcia-Ferrer Porras, A. Combining LiDAR Intensity with Aerial Camera Data to Discriminate Agricultural Land Uses. Comput. Electron. Agric. 2012, 84, 36–46. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.-P. Generalizing Predictive Models of Forest Inventory Attributes Using an Area-Based Approach with Airborne LiDAR Data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Wang, Q.; Pang, Y.; Chen, D.; Liang, X.; Lu, J. Lidar Biomass Index: A Novel Solution for Tree-Level Biomass Estimation Using 3D Crown Information. For. Ecol. Manag. 2021, 499, 119542. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining Spectral Reflectance Saturation in Landsat Imagery and Corresponding Solutions to Improve Forest Aboveground Biomass Estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Gong, W.; Xing, Y.; Hu, X.; Gong, J. Estimation of the Forest Stand Mean Height and Aboveground Biomass in Northeast China Using SAR Sentinel-1B, Multispectral Sentinel-2A, and DEM Imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 277–289. [Google Scholar] [CrossRef]
- Heurich, M.; Thoma, F. Estimation of Forestry Stand Parameters Using Laser Scanning Data in Temperate, Structurally Rich Natural European Beech (Fagus sylvatica) and Norway Spruce (Picea abies) Forests. Forestry 2008, 81, 645–661. [Google Scholar] [CrossRef] [Green Version]
- Nelson, R.; Short, A.; Valenti, M. Measuring Biomass and Carbon in Delaware Using an Airborne Profiling LIDAR. Scand. J. For. Res. 2004, 19, 500–511. [Google Scholar] [CrossRef]
- Clark, D.B.; Kellner, J.R. Tropical Forest Biomass Estimation and the Fallacy of Misplaced Concreteness. J. Veg. Sci. 2012, 23, 1191–1196. [Google Scholar] [CrossRef]
- Nelson, R.F.; Hyde, P.; Johnson, P.; Emessiene, B.; Imhoff, M.L.; Campbell, R.; Edwards, W. Investigating RaDAR–LiDAR Synergy in a North Carolina Pine Forest. Remote Sens. Environ. 2007, 110, 98–108. [Google Scholar] [CrossRef]
- Sarrazin, M.J.D.; van Aardt, J.A.N.; Asner, G.P.; McGlinchy, J.; Messinger, D.W.; Wu, J. Fusing Small-Footprint Waveform LiDAR and Hyperspectral Data for Canopy-Level Species Classification and Herbaceous Biomass Modeling in Savanna Ecosystems. Can. J. Remote Sens. 2011, 37, 653–665. [Google Scholar] [CrossRef]
- Labrecque, S.; Fournier, R.A.; Luther, J.E.; Piercey, D. A Comparison of Four Methods to Map Biomass from Landsat-TM and Inventory Data in Western Newfoundland. For. Ecol. Manag. 2006, 226, 129–144. [Google Scholar] [CrossRef]
- Tipton, J.; Opsomer, J.; Moisen, G. Properties of Endogenous Post-Stratified Estimation Using Remote Sensing Data. Remote Sens. Environ. 2013, 139, 130–137. [Google Scholar] [CrossRef]
- Breidenbach, J.; Nothdurft, A.; Kändler, G. Comparison of Nearest Neighbour Approaches for Small Area Estimation of Tree Species-Specific Forest Inventory Attributes in Central Europe Using Airborne Laser Scanner Data. Eur. J. For. Res. 2010, 129, 833–846. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, X.; Ouyang, Z.; Avitabile, V.; Qi, J.; Chen, J.; Giannico, V. Estimating Aboveground Biomass in Subtropical Forests of China by Integrating Multisource Remote Sensing and Ground Data. Remote Sens. Environ. 2019, 232, 111341. [Google Scholar] [CrossRef]
- Westfall, J.A.; Patterson, P.L.; Coulston, J.W. Post-Stratified Estimation: Within-Strata and Total Sample Size Recommendations. Can. J. For. Res. 2011, 41, 1130–1139. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Lu, D.; Chen, Q.; Keller, M.; Moran, E.; dos-Santos, M.N.; Bolfe, E.L.; Batistella, M. Examining Effective Use of Data Sources and Modeling Algorithms for Improving Biomass Estimation in a Moist Tropical Forest of the Brazilian Amazon. Int. J. Digit. Earth 2017, 10, 996–1016. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Xia, J.; Ha, N.T.; Le, N.N.; Nguyen, T.T.T.; Dao, T.H.; Vu, T.T.P.; Pham, T.D.; Takeuchi, W. Comparison of Machine Learning Methods for Estimating Mangrove Above-Ground Biomass Using Multiple Source Remote Sensing Data in the Red River Delta Biosphere Reserve, Vietnam. Remote Sens. 2020, 12, 1334. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ma, J.; Liang, S.; Li, X.; Li, M. An Evaluation of Eight Machine Learning Regression Algorithms for Forest Aboveground Biomass Estimation from Multiple Satellite Data Products. Remote Sens. 2020, 12, 4015. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of Feature Selection and CatBoost for Prediction: The First Application to the Estimation of Aboveground Biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Zhang, Q.; He, H.S.; Liang, Y.; Hawbaker, T.J.; Henne, P.D.; Liu, J.; Huang, S.; Wu, Z.; Huang, C. Integrating Forest Inventory Data and MODIS Data to Map Species-Level Biomass in Chinese Boreal Forests. Can. J. For. Res. 2018, 48, 461–479. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar Sampling for Large-Area Forest Characterization: A Review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef] [Green Version]
- Campbell, M.J.; Dennison, P.E.; Kerr, K.L.; Brewer, S.C.; Anderegg, W.R.L. Scaled Biomass Estimation in Woodland Ecosystems: Testing the Individual and Combined Capacities of Satellite Multispectral and Lidar Data. Remote Sens. Environ. 2021, 262, 112511. [Google Scholar] [CrossRef]
- Chen, Q.; Laurin, G.V.; Valentini, R. Uncertainty of Remotely Sensed Aboveground Biomass over an African Tropical Forest: Propagating Errors from Trees to Plots to Pixels. Remote Sens. Environ. 2015, 160, 134–143. [Google Scholar] [CrossRef]
- Chave, J.; Condit, R.; Aguilar, S.; Hernandez, A.; Lao, S.; Perez, R. Error Propagation and Scaling for Tropical Forest Biomass Estimates. Philos. Trans. R. Soc. B Biol. Sci. 2004, 359, 409–420. [Google Scholar] [CrossRef] [PubMed]
- Rammig, A.; Heinke, J.; Hofhansl, F.; Verbeeck, H.; Baker, T.R.; Christoffersen, B.; Ciais, P.; De Deurwaerder, H.; Fleischer, K.; Galbraith, D.; et al. A Generic Pixel-to-Point Comparison for Simulated Large-Scale Ecosystem Properties and Ground-Based Observations: An Example from the Amazon Region. Geosci. Model Dev. 2018, 11, 5203–5215. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Man, A.; Fredrickson, M.; Hou, Z.; Pitkanen, J.; Wing, B.; Ramirez, C.; Li, B.; Greenberg, J.A. Quantification of Uncertainty in Aboveground Biomass Estimates Derived from Small-Footprint Airborne LiDAR. Remote Sens. Environ. 2018, 216, 514–528. [Google Scholar] [CrossRef]
- Disney, M.I.; Kalogirou, V.; Lewis, P.; Prieto-Blanco, A.; Hancock, S.; Pfeifer, M. Simulating the Impact of Discrete-Return Lidar System and Survey Characteristics over Young Conifer and Broadleaf Forests. Remote Sens. Environ. 2010, 114, 1546–1560. [Google Scholar] [CrossRef]
- Garcia, M.; Saatchi, S.; Ferraz, A.; Silva, C.A.; Ustin, S.; Koltunov, A.; Balzter, H. Impact of Data Model and Point Density on Aboveground Forest Biomass Estimation from Airborne LiDAR. Carbon Balance Manag. 2017, 12, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hernández-Stefanoni, J.L.; Reyes-Palomeque, G.; Castillo-Santiago, M.Á.; George-Chacón, S.P.; Huechacona-Ruiz, A.H.; Tun-Dzul, F.; Rondon-Rivera, D.; Dupuy, J.M. Effects of Sample Plot Size and GPS Location Errors on Aboveground Biomass Estimates from LiDAR in Tropical Dry Forests. Remote Sens. 2018, 10, 1586. [Google Scholar] [CrossRef] [Green Version]
- Knapp, N.; Huth, A.; Fischer, R. Tree Crowns Cause Border Effects in Area-Based Biomass Estimations from Remote Sensing. Remote Sens. 2021, 13, 1592. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated Impact of Sample Plot Size and Co-Registration Error on the Accuracy and Uncertainty of LiDAR-Derived Estimates of Forest Stand Biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Roedig, E.; Knapp, N.; Fischer, R.; Bohn, F.J.; Dubayah, R.; Tang, H.; Huth, A. From Small-Scale Forest Structure to Amazon-Wide Carbon Estimates. Nat. Commun. 2019, 10, 5088. [Google Scholar] [CrossRef] [PubMed]










| Tree Species | Allometric Equation | Mean Carbon Conversion Factors |
|---|---|---|
| Picea asperata | AGB = 0.08070 × D2.25957 × H0.25663 | 0.4804 |
| Abies fabri | AGB = 0.06945 × D2.05753 × H0.50839 | 0.4805 |
| Larix gmelinii | AGB = 0.06848 × D2.01549 × H0.59146 | 0.4742 (Natural forest) 0.4674 (Plantation) |
| Pinus koraiensis | AGB = 0.027847 × D1.810004 × H0.905002 | 0.4809 |
| Populus davidiana | AGB = 0.02884 × D2.8785 | 0.4956 (Natural forest) 0.4761 (Plantation) |
| Ulmus pumila | AGB = 0.0607 × D2.4316 + 0.0678 × D1.9623 + 0.0148 × D1.9816 | 0.4648 |
| Betula platyphylla | AGB = 0.06807 × D2.10850 × H0.52019 | 0.4656 |
| Quercus mongolica | AGB = 0.06149 × D2.14380 × H0.58390 | 0.4802 |
| Tilia tuan | AGB = 0.01275 × D2.0188 × H1.0094 + 0.00182 × D1.9492 × H0.9746 + 0.00024 × D1.9814 × H0.9907 | 0.4677 |
| Forest Type | Number Of Plot | Forest AGC (Mg/ha) | ||||
|---|---|---|---|---|---|---|
| Total | Training Plot | Validation Plot | Range | Mean | Standard Deviation | |
| Coniferous forests | 591 | 473 | 118 | 1.40–82.30 | 26.23 | 13.09 |
| Broadleaf forests | 996 | 795 | 201 | 0.52–79.83 | 26.19 | 11.98 |
| All forests (non-stratification) | 1587 | 1267 | 320 | 0.52–82.30 | 26.20 | 12.35 |
| Dominant Species | Tree Species Composition | Number of Plot | Forest AGC (Mg/Ha) | ||||
|---|---|---|---|---|---|---|---|
| Total | Training Plot | Validation Plot | Range | Mean | Standard Deviation | ||
| Picea asperata and Abies fabri | Picea asperata dominant forests or Abies fabri dominant forests with a small mixture of Larix gmelinii | 197 | 158 | 39 | 2.29–82.30 | 30.73 | 15.35 |
| Larix gmelinii | Pure or Larix gmelinii dominant forests with a small mixture of Betula platyphylla and Populus davidiana | 197 | 158 | 39 | 1.40–56.13 | 25.33 | 12.11 |
| Pinus koraiensis | Pure or Pinus koraiensis dominant forests with a small mixture of Larix gmelinii | 197 | 158 | 39 | 1.44–49.13 | 22.64 | 9.96 |
| Populus davidiana | Pure or Populus davidiana dominant forests with a small mixture of Larix gmelinii | 209 | 167 | 42 | 0.52–79.83 | 34.36 | 17.44 |
| Ulmus pumila | Ulmus pumila dominant forests with a small mixture of Populus davidiana | 199 | 159 | 40 | 5.81–48.09 | 23.12 | 7.62 |
| Betula platyphylla | Pure or Betula platyphylla dominant forests with a small mixture of Larix gmelinii | 203 | 162 | 41 | 1.82–52.63 | 22.17 | 9.74 |
| Quercus mongolica | Quercus mongolica dominant forests with a small mixture of Pinus tabuliformis | 196 | 157 | 39 | 2.27–65.42 | 25.86 | 12.07 |
| Tilia tuan | Tilia tuan dominant forests with a small mixture of Larix gmelinii | 200 | 160 | 40 | 5.74–42.26 | 21.71 | 7.71 |
| LiDAR Metrics | Description |
|---|---|
| CC | Canopy cover |
| Canopy_relief_ratio | Canopy relief ratio |
| H_1, H_5, H_10, H_20, H_30,…H_80, H_90, H_95, H_99 | Height percentiles. Vertical distribution of point cloud height: 1%, 5%, 10%, 20%, 30%, …, 80%, 90%, 95%, 99% quantile |
| H_max | Maximum height |
| H_min | Minimum height |
| H_mean | Mean height |
| H_median | Median of height |
| H_madmedian | Median of median absolute deviation of height |
| H_sqrt_mean_sq | Generalized means for the 2nd power of height |
| H_curt_mean_cube | Generalized means for the 3rd power of height |
| H_AIH_IQ | Interquartile distance of cumulative height |
| H_IQ | Interquartile distance of height |
| H_skewness | Skewness of height |
| H_kurtosis | Kurtosis of height |
| H_aad | Average absolute deviation of height |
| H_cv | Coefficient of variation of height |
| H_stddev | Standard deviation of height |
| H_variance | Variance of height |
| Algorithm | Hyperparameter | Description | Value Ranges |
|---|---|---|---|
| RF | mtry | the number of predictor variables randomly sampled at each split | (1–n) n refers to the number of predictor variables |
| ntree | the number of trees | (100–1000) at intervals of 50 | |
| Cubist | committees | the number of trees | (1–100) at intervals of 1 |
| neighbors | controls the rule-based model predictions | (0–9) at intervals of 1 | |
| XGBoost | max_depth | the depth of the tree | (1–10) at intervals of 1 |
| eta | the learning rate | (0.01–0.5) at intervals of 0.01 | |
| gamma | minimum loss reduction of the tree | (0–1) at intervals of 0.1 | |
| colsample_bytree | the number of predictor variables supplied to a tree | (0–1) at intervals of 0.1 | |
| min_child_weight | minimum number of instances | (1–10) at intervals of 1 | |
| subsample | the number of observations supplied to a tree | (0–1) at intervals of 0.1 | |
| CatBoost | depth | the depth of the tree | (1–10) at intervals of 1 |
| learning_rate | the learning rate | (0.01–0.5) at intervals of 0.01 | |
| l2_leaf_reg | coefficient at the L2 regularization term of the cost function | (0–5) at intervals of 0.1 | |
| rsm | the percentage of features to use at each split selection | (0–1) at intervals of 0.1 |
| Forest Type | Model | R2 | RMSE (Mg/ha) | RRMSE (%) | MAE (Mg/ha) | Bias (Mg/ha) |
|---|---|---|---|---|---|---|
| All forests (non-stratification) | Stepwise | 0.3948 | 9.7867 | 39.0596 | 7.3902 | 0.8163 |
| RF | 0.4213 | 9.5699 | 38.1947 | 7.1368 | 0.8704 | |
| Cubist | 0.4119 | 9.6471 | 38.5028 | 7.0665 | −0.6283 | |
| XGBoost | 0.4392 | 9.4209 | 37.5998 | 7.0208 | 0.0435 | |
| CatBoost | 0.4411 | 9.4052 | 37.5374 | 7.0520 | 0.8851 | |
| Coniferous forests | Stepwise | 0.3911 | 9.4519 | 38.2231 | 7.0240 | 0.4808 |
| RF | 0.5853 | 7.8005 | 31.5447 | 5.9307 | 0.2851 | |
| Cubist | 0.5304 | 8.3004 | 33.5663 | 6.5400 | −0.0962 | |
| XGBoost | 0.6017 | 7.6441 | 30.9124 | 5.7157 | 0.1689 | |
| CatBoost | 0.6073 | 7.5907 | 30.6961 | 5.7559 | −0.1662 | |
| Broadleaf forests | Stepwise | 0.3577 | 9.9602 | 41.2753 | 7.7378 | 2.0755 |
| RF | 0.4249 | 9.4252 | 39.0582 | 7.0348 | 1.5388 | |
| Cubist | 0.3818 | 9.7718 | 40.4946 | 7.2849 | 0.6979 | |
| XGBoost | 0.4585 | 9.1452 | 37.8982 | 6.8907 | 1.7294 | |
| CatBoost | 0.4745 | 9.0093 | 37.3350 | 6.8652 | 1.6480 |
| Dominant Species | Model | R2 | RMSE (Mg/ha) | RRMSE (%) | MAE (Mg/ha) | Bias (Mg/ha) |
|---|---|---|---|---|---|---|
| Spruce–Fir | Stepwise | 0.7371 | 6.8977 | 23.4290 | 5.3067 | −0.1559 |
| RF | 0.7547 | 6.6623 | 22.6294 | 4.9116 | 0.1994 | |
| Cubist | 0.7493 | 6.7361 | 22.8801 | 5.2763 | 0.4992 | |
| XGBoost | 0.7936 | 6.1119 | 20.7600 | 4.5688 | −0.3968 | |
| CatBoost | 0.8175 | 5.7463 | 19.5181 | 4.2701 | 1.0252 | |
| Larch | Stepwise | 0.6931 | 6.5371 | 28.4119 | 4.9649 | 1.7802 |
| RF | 0.6273 | 7.2045 | 31.3124 | 5.8318 | 1.9752 | |
| Cubist | 0.6854 | 6.6184 | 28.7652 | 5.2080 | 0.5859 | |
| XGBoost | 0.7047 | 6.4125 | 27.8701 | 4.8272 | 1.1372 | |
| CatBoost | 0.7304 | 6.1274 | 26.6309 | 4.7103 | 1.1988 | |
| Red Pine | Stepwise | 0.7864 | 4.8843 | 21.8278 | 3.6780 | −1.0045 |
| RF | 0.8351 | 4.2915 | 19.1786 | 3.2918 | −0.7201 | |
| Cubist | 0.8014 | 4.7098 | 21.0482 | 3.8554 | −1.0005 | |
| XGBoost | 0.8509 | 4.0810 | 18.2380 | 3.3971 | −0.1736 | |
| CatBoost | 0.8699 | 3.8113 | 17.0328 | 3.2853 | 0.1476 | |
| Poplar | Stepwise | 0.6751 | 8.9241 | 23.6450 | 6.8659 | −0.9275 |
| RF | 0.7607 | 7.6595 | 20.2943 | 6.0103 | −0.0022 | |
| Cubist | 0.7486 | 7.8506 | 20.8007 | 6.1131 | 0.5429 | |
| XGBoost | 0.7778 | 7.3812 | 19.5569 | 5.8989 | 0.1414 | |
| CatBoost | 0.8054 | 6.9076 | 18.3022 | 5.2377 | −0.0178 | |
| White Birch | Stepwise | 0.7211 | 5.3155 | 24.7447 | 4.1372 | 0.2416 |
| RF | 0.7407 | 5.0642 | 23.5747 | 3.7654 | 0.2466 | |
| Cubist | 0.7662 | 4.8671 | 22.6570 | 3.5408 | −0.2407 | |
| XGBoost | 0.7636 | 4.8943 | 22.7840 | 3.5005 | 0.0718 | |
| CatBoost | 0.7852 | 4.6653 | 21.7180 | 3.6770 | −0.1229 | |
| Oak | Stepwise | 0.6362 | 6.6328 | 27.7826 | 4.8668 | 0.9758 |
| RF | 0.7468 | 5.5342 | 23.1808 | 4.0921 | 0.1669 | |
| Cubist | 0.7386 | 5.6229 | 23.5524 | 3.9071 | 0.1812 | |
| XGBoost | 0.7652 | 5.3294 | 22.3229 | 4.0862 | −0.5591 | |
| CatBoost | 0.7903 | 5.0355 | 21.0920 | 3.8465 | 0.3638 | |
| Linden | Stepwise | 0.3224 | 6.5837 | 30.2533 | 5.0754 | 0.7719 |
| RF | 0.5294 | 5.4869 | 25.2136 | 4.1952 | 0.4577 | |
| Cubist | 0.4821 | 5.7557 | 26.4485 | 4.2222 | 0.3208 | |
| XGBoost | 0.5450 | 5.3949 | 24.7906 | 4.1490 | 0.2983 | |
| CatBoost | 0.6327 | 4.8474 | 22.2750 | 3.8665 | 0.5140 | |
| Elm | Stepwise | 0.5362 | 4.8298 | 20.4512 | 3.9670 | 0.9204 |
| RF | 0.5959 | 4.5080 | 19.0887 | 3.7378 | 1.2237 | |
| Cubist | 0.5448 | 4.7845 | 20.2596 | 3.9858 | 1.1691 | |
| XGBoost | 0.6308 | 4.3089 | 18.2456 | 3.5939 | 0.9103 | |
| CatBoost | 0.6906 | 3.9446 | 16.7032 | 3.1906 | 0.5471 |
| Stratification Method | Model | R2 | RMSE (Mg/ha) | RRMSE (%) | MAE (Mg/ha) | Bias (Mg/ha) |
|---|---|---|---|---|---|---|
| Non-stratification | Stepwise regression | 0.3948 | 9.7867 | 39.0596 | 7.3902 | 0.8163 |
| RF | 0.4213 | 9.5699 | 38.1947 | 7.1368 | 0.8704 | |
| Cubist | 0.4119 | 9.6471 | 38.5028 | 7.0665 | −0.6283 | |
| XGBoost | 0.4392 | 9.4209 | 37.5998 | 7.0208 | 0.0435 | |
| CatBoost | 0.4411 | 9.4052 | 37.5374 | 7.0520 | 0.8851 | |
| FTS | Stepwise regression | 0.3700 | 9.7752 | 40.1415 | 7.4738 | 1.4856 |
| RF | 0.4826 | 8.8590 | 36.3788 | 6.6264 | 1.0751 | |
| Cubist | 0.4353 | 9.2548 | 38.0042 | 7.0094 | 0.4042 | |
| XGBoost | 0.5101 | 8.6205 | 35.3995 | 6.4561 | 1.1522 | |
| CatBoost | 0.5223 | 8.5121 | 34.9546 | 6.4549 | 0.9769 | |
| DSS | Stepwise regression | 0.7309 | 6.4663 | 25.3713 | 4.8700 | 0.3162 |
| RF | 0.7737 | 5.9307 | 23.2698 | 4.5070 | 0.4091 | |
| Cubist | 0.7705 | 5.9719 | 23.4313 | 4.5200 | 0.2599 | |
| XGBoost | 0.7984 | 5.5975 | 21.9624 | 4.2611 | 0.1803 | |
| CatBoost | 0.8232 | 5.2421 | 20.5680 | 4.0169 | 0.4493 |
| Factor | Df | R2 SumSq | η2 | RMSE SumSq | η2 | RRMSE SumSq | η2 | MAE SumSq | η2 |
|---|---|---|---|---|---|---|---|---|---|
| Stratification | 2 | 0.65 | 0.53 | 123.45 | 0.66 | 2171.4 | 0.77 | 63.89 | 0.64 |
| Regression method | 4 | 0.10 | 0.08 | 8.39 | 0.05 | 131.1 | 0.05 | 4.51 | 0.05 |
| Stratification: regression method | 8 | 0.01 | 0.01 | 0.68 | 0.00 | 11.5 | 0.00 | 0.50 | 0.01 |
| Residuals | 40 | 0.47 | 53.52 | 511.3 | 30.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Qiu, X.; Zeng, W.; Peng, D. Combining Sample Plot Stratification and Machine Learning Algorithms to Improve Forest Aboveground Carbon Density Estimation in Northeast China Using Airborne LiDAR Data. Remote Sens. 2022, 14, 1477. https://doi.org/10.3390/rs14061477
Chen M, Qiu X, Zeng W, Peng D. Combining Sample Plot Stratification and Machine Learning Algorithms to Improve Forest Aboveground Carbon Density Estimation in Northeast China Using Airborne LiDAR Data. Remote Sensing. 2022; 14(6):1477. https://doi.org/10.3390/rs14061477
Chicago/Turabian StyleChen, Mingjie, Xincai Qiu, Weisheng Zeng, and Daoli Peng. 2022. "Combining Sample Plot Stratification and Machine Learning Algorithms to Improve Forest Aboveground Carbon Density Estimation in Northeast China Using Airborne LiDAR Data" Remote Sensing 14, no. 6: 1477. https://doi.org/10.3390/rs14061477
APA StyleChen, M., Qiu, X., Zeng, W., & Peng, D. (2022). Combining Sample Plot Stratification and Machine Learning Algorithms to Improve Forest Aboveground Carbon Density Estimation in Northeast China Using Airborne LiDAR Data. Remote Sensing, 14(6), 1477. https://doi.org/10.3390/rs14061477