Simulative Evaluation of the Underwater Geodetic Network Configuration on Kinematic Positioning Performance
Abstract
:1. Introduction
2. Methods
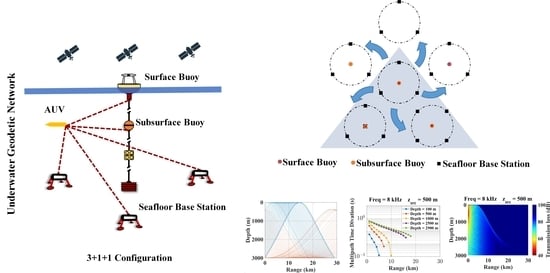
2.1. Underwater Geodetic Network Design
2.2. Underwater Environmental Factors
2.3. Kinematic Positioning Performance Assessment Methods
- Available Station Number (ASN) and Effective Positioning Grid (EPG)
- Position Dilution of Precision (PDOP)
3. Results and Discussion
3.1. Evaluation of Network Kinematic Positioning Performance
3.2. Impact of Network Dimension on Positioning Performance
3.3. Impact of Network Configuration on Positioning Performance
3.3.1. Configuration without Buoys
3.3.2. Configuration with More Seafloor Base Stations
3.4. Impact of Acoustic Transmission Characteristics on Acoustic Signal Propagation
3.4.1. Acoustic Ray Bending
3.4.2. Multipath and Doppler Effects
3.4.3. Acoustic Transmission Loss
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Liu, Y.; Sun, D.; Xu, T.; Xue, S.; Han, Y.; Zeng, A. Seafloor geodetic network establishment and key technologies. Sci. China Earth Sci. 2020, 50, 936–945. [Google Scholar] [CrossRef]
- Batista, P.; Silvestre, C.; Oliveira, P. A Sensor-based Long Baseline Position and Velocity Navigation Filter for Underwater Vehicles. IFAC Proc. Vol. 2010, 43, 302–307. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Han, Y.; Zheng, C.; Sun, D. Underwater target localization using long baseline positioning system. Appl. Acoust. 2016, 111, 129–134. [Google Scholar] [CrossRef]
- Spiess, F.N. Analysis of a possible sea floor strain measurement system. Mar. Geod. 1985, 9, 385–398. [Google Scholar] [CrossRef]
- Spiess, F.N.; Chadwell, C.D.; Hildebrand, J.A.; Young, L.E.; Purcell, G.H., Jr.; Dragert, H. Precise GPS/Acoustic positioning of seafloor reference points for tectonic studies. Phys. Earth Planet. Inter. 1998, 108, 101–112. [Google Scholar] [CrossRef]
- Chadwell, C.D. Shipboard towers for Global Positioning System antennas. Ocean Eng. 2003, 30, 1467–1487. [Google Scholar] [CrossRef]
- Gagnon, K.; Chadwell, C.D.; Norabuena, E. Measuring the onset of locking in the Peru-Chile trench with GPS and acoustic measurements. Nature 2005, 434, 205. [Google Scholar] [CrossRef] [PubMed]
- Chadwell, C.D.; Spiess, F.N. Plate motion at the ridge-transform boundary of the south Cleft segment of the Juan de Fuca Ridge from GPS-Acoustic data. J. Geophys. Res. Solid Earth 2008, 113, B04415. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Qin, X. Resilient observation models for seafloor geodetic positioning. J. Geod. 2021, 95, 79. [Google Scholar] [CrossRef]
- Techy, L.; Morganseny, K.A.; Woolseyz, C.A. Long-baseline acoustic localization of the Seaglider underwater glider. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 3990–3995. [Google Scholar]
- Iinuma, T.; Kido, M.; Ohta, Y.; Fukuda, T.; Tomita, F.; Ueki, I. GNSS-Acoustic Observations of Seafloor Crustal Deformation Using a Wave Glider. Front. Earth Sci. 2021, 9, 600946. [Google Scholar] [CrossRef]
- Kinsey, J.; Eustice, R.; Whitcomb, L. A Survey of Underwater Vehicle Navigation: Recent Advances and New Challenges. In Proceedings of the Conference of Manoeuvering and Control of Marine Craft, Lisbon, Portugal, 20–22 September 2006; pp. 1–12. [Google Scholar]
- Sun, D.; Zheng, C.; Zhang, J.; Han, Y.; Cui, H. Development and Prospect for Underwater Acoustic Positioning and Navigation Technology. Bull. Chin. Acad. Sci. 2019, 34, 331–338. [Google Scholar] [CrossRef]
- High-Depths USBL Positioning System. Available online: https://www.ixblue.com/products/posidonia (accessed on 10 April 2022).
- Sun, W.; Liu, Q.; Yin, X.; Liu, J. A method of calculating the maximum mutually measuring distances between the transponders. Hydrogr. Surv. Chart. 2019, 39, 10–13. [Google Scholar] [CrossRef]
- Alcocer, A.; Oliveira, P.; Pascoal, A. Underwater acoustic positioning systems based on buoys with GPS. In Proceedings of the Eighth European Conference on Underwater Acoustics, Carvoeiro, Portugal, 12–15 June 2006; Volume 8, pp. 1–8. [Google Scholar]
- Burgmann, R.; Chadwell, D. Seafloor Geodesy. Annu. Rev. Earth Planet. Sci. 2014, 42, 509–534. [Google Scholar] [CrossRef]
- Blum, J.A.; Chadwell, C.D.; Driscoll, N.; Zumberge, M.A. Assessing slope stability in the Santa Barbara Basin, California, using seafloor geodesy and CHIRP seismic data. Geophys. Res. Lett. 2010, 37, 438–454. [Google Scholar] [CrossRef]
- Imano, M.; Kido, M.; Ohta, Y.; Fukuda, T.; Ochi, H.; Takahashi, N.; Hino, R. Improvement in the Accuracy of Real-Time GPS/Acoustic Measurements Using a Multi-Purpose Moored Buoy System by Removal of Acoustic Multipath. In Proceedings of the International Symposium on Geodesy for Earthquake and Natural Hazards, Matsushima, Japan, 22–26 July 2014; pp. 105–114. [Google Scholar]
- Ikuta, R.; Tadokoro, K.; Ando, M.; Okuda, T.; Sugimoto, S.; Takatani, K.; Yada, K.; Besana, G.M. A new GPS-acoustic method for measuring ocean floor crustal deformation: Application to the Nankai Trough. J. Geophys. Res. Solid Earth 2008, 113, B02041. [Google Scholar] [CrossRef] [Green Version]
- Tadokoro, K.; Kinugasa, N.; Kato, T.; Terada, Y.; Matsuhiro, K. A Marine-Buoy-Mounted System for Continuous and Real-Time Measurment of Seafloor Crustal Deformation. Front. Earth Sci. 2020, 8, 123. [Google Scholar] [CrossRef]
- Kido, M.; Fujimoto, H.; Hino, R.; Ohta, Y.; Osada, Y.; Iinuma, T.; Azuma, R.; Wada, I.; Miura, S.; Suzuki, S. Progress in the Project for Development of GPS/Acoustic Technique Over the Last 4 Years. In Proceedings of the International Symposium on Geodesy for Earthquake and Natural Hazards (GENAH), Matsushima, Japan, 22–26 July 2014; Springer: Cham, Switzerland, 2015; pp. 3–10. [Google Scholar] [CrossRef]
- Imano, M.; Kido, M.; Honsho, C.; Ohta, Y.; Takahashi, N.; Fukuda, T.; Ochi, H.; Hino, R. Assessment of directional accuracy of GNSS-Acoustic measurement using a slackly moored buoy. Prog. Earth Planet. Sci. 2019, 6, 56. [Google Scholar] [CrossRef] [Green Version]
- Chadwell, C.D. GPS-Acoustic Seafloor Geodesy using a Wave Glider. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 9–13 December 2013; Volume 2013, p. G14A-01. [Google Scholar]
- Yokota, Y.; Matsuda, T. Underwater Communication Using UAVs to Realize High-Speed AUV Deployment. Remote Sens. 2021, 13, 4173. [Google Scholar] [CrossRef]
- Zhao, J.; Zou, Y.; Zhang, H.; Wu, Y.; Fang, S. A new method for absolute datum transfer in seafloor control network measurement. J. Mar. Sci. Technol. 2016, 21, 216–226. [Google Scholar] [CrossRef]
- Chen, G.; Liu, Y.; Liu, Y.; Liu, J. Improving GNSS-acoustic positioning by optimizing the ship’s track lines and observation combinations. J. Geod. 2020, 94, 61. [Google Scholar] [CrossRef]
- Nakamura, Y.; Yokota, Y.; Ishikawa, T.; Watanabe, S. Optimal Transponder Array and Survey Line Configurations for GNSS-A Observation Evaluated by Numerical Simulation. Front. Earth Sci. 2021, 9, 33. [Google Scholar] [CrossRef]
- Matsui, R.; Kido, M.; Niwa, Y.; Honsho, C. Effects of disturbance of seawater excited by internal wave on GNSS-acoustic positioning. Mar. Geophys. Res. 2019, 40, 541–555. [Google Scholar] [CrossRef]
- Watanabe, S.; Ishikawa, T.; Yokota, Y.; Nakamura, Y. GARPOS: Analysis Software for the GNSS-A Seafloor Positioning with Simultaneous Estimation of Sound Speed Structure. Front. Earth Sci. 2020, 8, 508. [Google Scholar] [CrossRef]
- Diamant, R.; Lampe, L. Underwater Localization with Time-Synchronization and Propagation Speed Uncertainties. IEEE Trans. Mob. Comput. 2013, 12, 1257–1269. [Google Scholar] [CrossRef]
- Norgren, P.; Skjetne, R. Using Autonomous Underwater Vehicles as Sensor Platforms for Ice-Monitoring. Model. Identif. Control 2014, 35, 263–277. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Chen, G.; Zhao, J.; Gao, K.; Liu, Y. Development and Trends of Marine Space-Time Frame Network. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 17–37. [Google Scholar] [CrossRef]
- Warren, D.M.; Raquet, J. Broadcast vs. precise GPS ephemerides: A historical perspective. GPS Solut. 2003, 7, 151–156. [Google Scholar] [CrossRef]
- Kido, M.; Osada, Y.; Fujimoto, H. Temporal variation of sound speed in ocean: A comparison between GPS/acoustic and in situ measurements. Earth Planets Space 2008, 60, 229–234. [Google Scholar] [CrossRef] [Green Version]
- Xue, S.; Yang, Y. Positioning configurations with the lowest GDOP and their classification. J. Geod. 2015, 89, 49–71. [Google Scholar] [CrossRef]
- Beavan, J. Noise properties of continuous GPS data from concrete pillar geodetic monuments in New Zealand and comparison with data from U.S. deep drilled braced monuments. J. Geophys. Res. Solid Earth 2005, 110, B08410. [Google Scholar] [CrossRef]
- Morozs, N.; Gorma, W.; Henson, B.; Shen, L.; Mitchell, P.; Zakharov, Y. Channel Modeling for Underwater Acoustic Network Simulation. IEEE Access 2020, 8, 136151–136175. [Google Scholar] [CrossRef]
- Munk, W.H. Sound channel in an exponentially stratified ocean, with application to SOFAR. J. Acoust. Soc. Am. 1974, 55, 220–226. [Google Scholar] [CrossRef]
- Chadwell, C.D.; Sweeney, A.D. Acoustic Ray-Trace Equations for Seafloor Geodesy. Mar. Geod. 2010, 33, 164–186. [Google Scholar] [CrossRef]
- Sweeney, A.D.; Chadwell, C.D.; Hildebrand, J.A.; Spiess, F.N. Centimeter-Level Positioning of Seafloor Acoustic Transponders from a Deeply-Towed Interrogator. Mar. Geod. 2005, 28, 39–70. [Google Scholar] [CrossRef]
- Honsho, C.; Kido, M.; Ichikawa, T.; Ohashi, T.; Kawakami, T.; Fujimoto, H. Application of Phase-Only Correlation to Travel-Time Determination in GNSS-Acoustic Positioning. Front. Earth Sci. 2021, 9, 7. [Google Scholar] [CrossRef]
- Tadokoro, K.; Ikuta, R.; Watanabe, T.; Ando, M.; Okuda, T.; Nagai, S.; Yasuda, K.; Sakata, T. Interseismic seafloor crustal deformation immediately above the source region of anticipated megathrust earthquake along the Nankai Trough, Japan. Geophys. Res. Lett. 2012, 39, L10306. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Liu, Y.; Liu, Y.; Chen, G.; Tang, Q.; Han, Y.; Wen, Y. Simulative Evaluation of the Underwater Geodetic Network Configuration on Kinematic Positioning Performance. Remote Sens. 2022, 14, 1939. https://doi.org/10.3390/rs14081939
Li M, Liu Y, Liu Y, Chen G, Tang Q, Han Y, Wen Y. Simulative Evaluation of the Underwater Geodetic Network Configuration on Kinematic Positioning Performance. Remote Sensing. 2022; 14(8):1939. https://doi.org/10.3390/rs14081939
Chicago/Turabian StyleLi, Menghao, Yang Liu, Yanxiong Liu, Guanxu Chen, Qiuhua Tang, Yunfeng Han, and Yuanlan Wen. 2022. "Simulative Evaluation of the Underwater Geodetic Network Configuration on Kinematic Positioning Performance" Remote Sensing 14, no. 8: 1939. https://doi.org/10.3390/rs14081939
APA StyleLi, M., Liu, Y., Liu, Y., Chen, G., Tang, Q., Han, Y., & Wen, Y. (2022). Simulative Evaluation of the Underwater Geodetic Network Configuration on Kinematic Positioning Performance. Remote Sensing, 14(8), 1939. https://doi.org/10.3390/rs14081939