Soil Moisture Retrieval from the CyGNSS Data Based on a Bilinear Regression
Abstract
:1. Introduction
2. Datasets
2.1. CyGNSS Remote Sensing Data
2.2. Reference SMAP Products
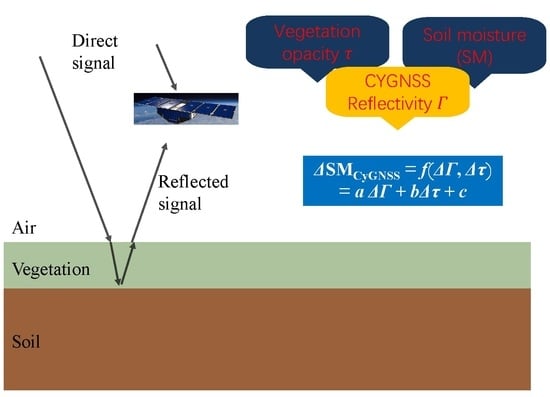
3. SM Retrieval Method
Modeling of
4. Experiments and Evaluation
4.1. Determination of the Coefficients
4.2. Validation and Assessment
4.3. Sensitivity of to and
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SM | Soil Moisture |
| GNSS | Global Navigation Satellite System |
| VOD | Vegetation Optical Depth |
| CyGNSS | Cyclone GNSS |
| SMAP | Soil Moisture Active Passive |
| RMSEs | Root-Mean-Square Errors |
| SMOS | Soil Moisture and Ocean Salinity |
| GNSS-R | Global Navigation Satellite System-Reflectometry |
| ML | Machine Learning |
| BR | Bilinear Regression |
| BRCS | Bistatic Radar Cross Section |
| SNR | Signal-To-Noise Ratio |
| SP | Specular Point |
| LUTs | Lookup Tables |
References
- Bennett, A.C.; Penman, T.D.; Arndt, S.K.; Roxburgh, S.H.; Bennett, L.T. Climate more important than soils for predicting forest biomass at the continental scale. Ecography 2020, 43, 1692–1705. [Google Scholar] [CrossRef]
- Dobriyal, P.; Qureshi, A.; Badola, R.; Hussain, S.A. A review of the methods available for estimating soil moisture and its implications for water resource management. J. Hydrol. 2012, 458–459, 110–117. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M.A. Microwave dielectric behavior of wet soil-Part II: Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.M.; Font, J.; Berger, M. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil moisture mapping using Sentinel-1 images: Algorithm and preliminary validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar] [CrossRef]
- Aubert, M.; Baghdadi, N.; Zribi, M.; Douaoui, A.; Loumagne, C.; Baup, F.; El Hajj, M.; Garrigues, S. Analysis of TerraSAR-X data sensitivity to bare soil moisture, roughness, composition and soil crust. Remote Sens. Environ. 2011, 115, 1801–1810. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Komjathy, A. GNSS reflectometry and remote sensing: New objectives and results. Adv. Sp. Res. 2010, 46, 111–117. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Feng, G.; Gleason, S. Remote sensing using GNSS signals: Current status and future directions. Adv. Sp. Res. 2011, 47, 1645–1653. [Google Scholar] [CrossRef]
- De Roo, R.D.; Ulaby, F.T. Bistatic specular scattering from rough dielectric surfaces. IEEE Trans. Antennas Propag. 1994, 42, 220–231. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S.; Jales, P.; Gommenginger, C. Spaceborne GNSS-R minimum variance wind speed estimator. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6829–6843. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Roselló, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Collett, I.; Morton, Y.J. Application of neural network to GNSS-R wind speed retrieval. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9756–9766. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Martin-Neira, M.; Fabra, F.; Nogues-Correig, O.; Ribo, S.; Kainulainen, J.; Camps, A.; D’Addio, S. Consolidating the precision of interferometric GNSS-R ocean altimetry using airborne experimental data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4992–5004. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Spaceborne GNSS-R sea ice detection using delay-Doppler maps: First results from the U.K. TechDemoSat-1 mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4795–4801. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; O’Brien, A.J.; Balenzano, A.; Mattia, F. Time-series retrieval of soil moisture using CYGNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4322–4331. [Google Scholar] [CrossRef]
- Chew, C.; Small, E. Description of the UCAR/CU soil moisture product. Remote Sens. 2020, 12, 1558. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E. Soil moisture sensing using spaceborne GNSS reflections: Comparison of CYGNSS reflectivity to SMAP soil moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef] [Green Version]
- Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CYGNSS data for soil moisture retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Dong, Z.; Jin, S. Evaluation of the land GNSS-Reflected DDM coherence on soil moisture estimation from CYGNSS data. Remote Sens. 2021, 13, 570. [Google Scholar] [CrossRef]
- Eroglu, O.; Kurum, M.; Boyd, D.; Gurbuz, A.C. High spatio-temporal resolution CYGNSS soil moisture estimates using artificial neural networks. Remote Sens. 2019, 11, 2272. [Google Scholar] [CrossRef] [Green Version]
- Santi, E.; Pettinato, S.; Paloscia, S.; Clarizia, M.P.; Dente, L.; Guerriero, L.; Comite, D.; Pierdicca, N. Soil moisture and forest biomass retrieval on a global scale by using CyGNSS data and artificial neural networks. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2905–5907. [Google Scholar]
- Senyurek, V.; Lei, F.; Boyd, D.; Gurbuz, A.C.; Kurum, M.; Moorhead, R. Evaluations of machine learning-based CYGNSS soil moisture estimates against SMAP observations. Remote Sens. 2020, 12, 3503. [Google Scholar] [CrossRef]
- Yan, Q.; Gong, S.; Jin, S.; Huang, W.; Zhang, C. Near real-time soil moisture in China retrieved from CyGNSS reflectivity. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Jin, S.; Jia, Y. Pan-tropical soil moisture mapping based on a three-layer model from CYGNSS GNSS-R data. Remote Sens. Environ. 2020, 247, 111947. [Google Scholar] [CrossRef]
- Yang, T.; Wan, W.; Sun, Z.; Liu, B.; Li, S.; Chen, X. Comprehensive evaluation of using TechDemoSat-1 and CYGNSS data to estimate soil moisture over mainland China. Remote Sens. 2020, 12, 1699. [Google Scholar] [CrossRef]
- Chew, C. Spatial interpolation based on previously-observed behavior: A framework for interpolating spaceborne GNSS-R data from CYGNSS. J. Spat. Sci. 2021. [Google Scholar] [CrossRef]
- O’Neill, P.E.; Chan, S.; Njoku, E.G.; Jackson, T.; Bindlish, R. SMAP L3 Radiometer Global Daily 36 km EASE-Grid Soil Moisture; Version 7; National Snow and Ice Data Center: Boulder, CO, USA, 2020. [Google Scholar]
- Carreno-Luengo, H.; Camps, A.; Querol, J.; Forte, G. First results of a GNSS-R experiment from a stratospheric balloon over boreal forests. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2652–2663. [Google Scholar] [CrossRef] [Green Version]
- Choudhury, B.J.; Schmugge, T.J.; Chang, A.; Newton, R.W. Effect of surface roughness on the microwave emission from soils. J. Geophys. Res. 1979, 89, 5699–5706. [Google Scholar] [CrossRef]
- Balenzano, A.; Mattia, F.; Satalino, G.; Davidson, M.W. Dense temporal series of C- and L-band SAR data for soil moisture retrieval over Agricultural Crops. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 439–450. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Borgeaud, M.; Rott, H. A study of vegetation cover effects on ers scatterometer data. IEEE Trans. Geosci. Remote Sens. 1999, 37, 938–948. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Jackson, T.J.; O’Neill, P.; De Lannoy, G.; de Rosnay, P.; Walker, J.P.; Ferrazzoli, P.; Mironov, V.; Bircher, S.; Grant, J.P.; et al. Modelling the passive microwave signature from land surfaces: A review of recent results and application to the L-band SMOS & SMAP soil moisture retrieval algorithms. Remote Sens. Environ. 2017, 192, 238–262. [Google Scholar] [CrossRef]
















| Land Type | (cm/cm) | ||||
|---|---|---|---|---|---|
| Barren or Sparsely Vegetated | 0.0594 | 0.0010 | 0.0248 | 48.1977 | −0.0002 |
| Open Shrublands | 0.0873 | 0.0609 | 0.0589 | 1.9156 | 0.0015 |
| Grasslands | 0.1487 | 0.1211 | 0.0812 | 0.7078 | 0.0039 |
| Savannas | 0.1584 | 0.3454 | 0.0785 | 0.7335 | 0.0067 |
| Cropland/Natural Vegetation Mosaic | 0.2001 | 0.2736 | 0.1225 | 0.6106 | 0.0074 |
| Woody Savannas | 0.2329 | 0.4912 | 0.0710 | 1.0443 | 0.0076 |
| Expression | |||||
|---|---|---|---|---|---|
| Category | Measure | ||||
| Training | r (SM) | 0.98 | 0.97 | 0.96 | 0.95 |
| r () | 0.91 | 0.90 | 0.81 | 0.79 | |
| RMSE | 0.019 | 0.022 | 0.027 | 0.028 | |
| Test | r (SM) | 0.95 | 0.93 | 0.93 | 0.91 |
| r () | 0.81 | 0.80 | 0.72 | 0.62 | |
| RMSE | 0.029 | 0.034 | 0.035 | 0.037 | |
| Overall | r (SM) | 0.97 | 0.95 | 0.95 | 0.94 |
| r () | 0.86 | 0.86 | 0.77 | 0.71 | |
| RMSE | 0.024 | 0.028 | 0.031 | 0.033 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Yan, Q.; Jin, S.; Huang, W.; Chen, T.; Jia, Y.; Liu, S.; Cao, Q. Soil Moisture Retrieval from the CyGNSS Data Based on a Bilinear Regression. Remote Sens. 2022, 14, 1961. https://doi.org/10.3390/rs14091961
Chen S, Yan Q, Jin S, Huang W, Chen T, Jia Y, Liu S, Cao Q. Soil Moisture Retrieval from the CyGNSS Data Based on a Bilinear Regression. Remote Sensing. 2022; 14(9):1961. https://doi.org/10.3390/rs14091961
Chicago/Turabian StyleChen, Sizhe, Qingyun Yan, Shuanggen Jin, Weimin Huang, Tiexi Chen, Yan Jia, Shuci Liu, and Qing Cao. 2022. "Soil Moisture Retrieval from the CyGNSS Data Based on a Bilinear Regression" Remote Sensing 14, no. 9: 1961. https://doi.org/10.3390/rs14091961
APA StyleChen, S., Yan, Q., Jin, S., Huang, W., Chen, T., Jia, Y., Liu, S., & Cao, Q. (2022). Soil Moisture Retrieval from the CyGNSS Data Based on a Bilinear Regression. Remote Sensing, 14(9), 1961. https://doi.org/10.3390/rs14091961