Geospatial Modelling for Delineation of Crop Management Zones Using Local Terrain Attributes and Soil Properties

Abstract

Defining nutrient management zones (MZs) is crucial for the implementation of site-specific management. The determination of MZs is based on several factors, including crop, soil, climate, and terrain characteristics. This study aims to delineate MZs by means of geostatistical and fuzzy clustering algorithms considering remotely sensed and laboratory data and, subsequently, to compare the zone maps in the north-eastern Himalayan region of India. For this study, 896 grid-wise representative soil samples (0–25 cm depth) were collected from the study area (1615 km²). The soils were analysed for soil reaction (pH), soil organic carbon and available macro (N, P and K) and micronutrients (Fe, Mn, Zn and Cu). The predicted soil maps were developed using regression kriging, where 28 digital elevation model-derived terrain attributes and two vegetation derivatives were used as environmental covariates. The coefficient of determination (R²) and root mean square error were used to evaluate the model’s performance. The predicted soil parameters were accurate, and regression kriging identified the highest variability for the majority of the soil variables. Further, to define the management zones, the geographically weighted principal component analysis and possibilistic fuzzy c-means clustering method were employed, based on which the optimum clusters were identified by employing fuzzy performance index and normalized classification entropy. The management zones were constructed considering the total pixel points of 30 m spatial resolution (17, 86,985 data points). The area was divided into four distinct zones, which could be differently managed. MZ 1 covers the maximum (43.3%), followed by MZ 2 (29.4%), MZ 3 (27.0%) and MZ 4 (0.3%). The MZs map thus would not only serve as a guide for judicious location-specific nutrient management, but would also help the policymakers to bring sustainable changes in the north-eastern Himalayan region of India.

1. Introduction

Agricultural nutrient management is complicated by soil variability. The variation in soil fertility to support optimal crop production is a global concern. The growth in crop production was found to decelerate in all regions, particularly in developed countries and also in East Asia [1]. Several factors limit agricultural production by affecting crops, namely climatic, edaphic and biotic factors. At present, the major cause of declining global crop production is soil degradation. Soil degradation, as measured by diminishing fertility, is a key factor limiting the crop yield in many regions of the world, including India’s north-eastern region [2]. The spatial variability of soil nutrients is affected by the landform, soil type, vegetation, climate and different anthropogenic activities. Moreover, hilly and mountainous regions influence the spatial variability of soils due to the wide range of environmental factors. Improper application of fertilizers in highly variable soils has increasingly become a serious threat to sustainable crop production and, at the same time, fertilizer losses have some associated environmental hazards [3,4]. On the other hand, deficiency of nutrients is more prevalent in all agricultural soils and crops. Blanket fertilizer application in fields often leads to over and under input application [5]. To achieve a high return with less adverse impacts on the environment, fertilizer application in excess should be avoided [6]. Hence, the calibration of fertilizer rates based on estimates to achieve a targeted yield is required to address spatial variability within targeted fields [7,8]. Therefore, efficient techniques should be implemented to precisely gauge variations in soil attributes within the fields, which is important for delineating homogeneous management zones (MZs) [9]. Wide variation in content, as well as in the availability of soil nutrients is present both within and between the fields [5]. Most of these studies were based on agro-ecological zones that were similar in topography, climate and the major soil types. The wide variation within the study area was hypothesized considering varying degrees of terrain attributes that affect soil biogeochemical properties. In the predictive models, different covariates, e.g., terrain factors, climate and remotely sensed imagery, are widely used [10]. However, terrain with digital elevation model (DEM) derivatives would be the main predictor variable, as it is easily quantified and correlated directly with the state factors [11].

Recently, digital soil mapping (DSM) approaches have been used to estimate the distribution of soil attributes at spatial scales [12]. The delineation of MZs with the aid of DSM helps to enhance site-specific nutrient management (SSNM) more sustainably. The delineation of management zones (MZs) by creating several subsets in an area based on homogeneous soil or plant properties is the most popular [13]. However, to delineate the proper MZs of an area, better know-how regarding soil fertility status is of utmost importance and ultimately assists in better crop management and environmental protection. Several scholars have employed principal component analysis (PCA) and fuzzy c-means clustering to designate MZs based on soil properties, among other approaches [14,15,16]. In addition to this, numerous alternate methods viz. top sheet and soil survey [17], crop yield-based management zone techniques [18,19] and nutrient index techniques [20,21,22] were utilized for delineating management zones.

Recently, two prime steps involved in the delineation of MZs are the use of PCA to reduce the dataset and their subsequent classification into management areas by using cluster analysis. PCA is mostly used to characterize the relationship between attributes and related environmental factors, and the subsequent quantification of the spatial variability pattern of these attributes [23,24,25]. However, the major limitation of any standard aspatial statistic is that it does not account for geographical variations in the observed value or any relationship between them [26]. Moreover, PCA does not consider spatial relationships and was not designed for the identification of spatial structures [27]. Geographically weighted PCA (GWPCA) can be used to address such limitations of PCA in which weights are fixed based on the location of each sampling point [26,28]. This methodology is used to study the correlation between each soil attribute and locally derived components, and thus consider geographic variations in numerous soil attributes across space. Later work involves several cluster analyses, and several researchers have used several clustering techniques to classify management zones, such as c-means [29], possibilistic c-means (PCM) [30], and fuzzy c-means (FCM) [9]. However, possibilistic fuzzy c-means (PFCM), which inherits the properties of both PCM and FCM, has a better clustering algorithm that reduces the coincidence of clustering as well as noisy sensitivity. Therefore, PFCM gives more value to typicality or membership values [31].

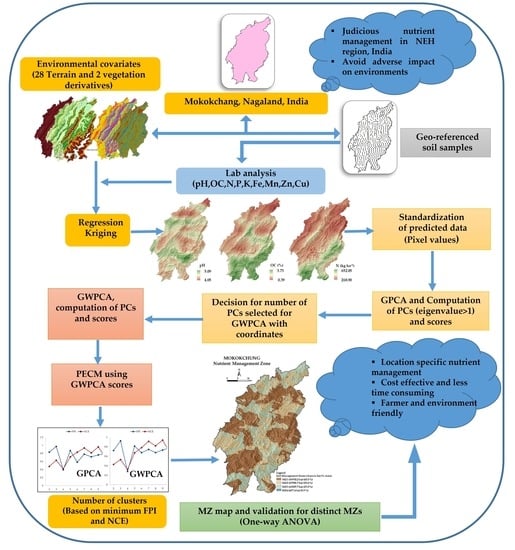
The north-eastern Himalayan region of India (NEHR) is a unique fragile ecosystem due to its strategic setting, occupying 8% of the total geographical area (TGA) of the country. Soil nutrient losses pose a threat to crop cultivation due to undulating terrain with steep ridges and intermountain valleys [32]. However, data regarding the variability of soil nutrients at a regional scale in the NEHR of India are very limited. Here we aimed to utilize the GWPCA algorithm to explore these fertility parameters through a case study, evaluating the degree of spatial correlation among the surface soil nutrients. More particularly, studies that use GWPCA are very limited, and none of them have evaluated the spatial distribution of the soil nutrients. Keeping this as background information, the present study was conducted (a) to predict the spatial distribution of soil attributes and available nutrients using the regression kriging approach, (b) to identify possible management zones (MZs) using GWPCA and PFCM and (c) to study the potential of the identified MZs for site-specific nutrient and crop management in the NEHR of India.

2. Materials and Methods

2.1. Details of the Study Area

The study was conducted in the Mokokchung district of Nagaland state in India, lying in the north-eastern Himalayan region. The region lies between 26°11′33.01″N to 26°45′47.18″N latitude and 94°17′36.74″E to 94°45′34.45″E longitude, with a total area of 1615 km² (Figure 1). It shares its boundary with the Longleng and Tuensang districts in the east, Wokha district in the west, Zunheboto district in the south of the Nagaland state and Assam state in the north. The climate varies from hot to warm sub-tropical to warm sub-temperate type depending upon the elevation variations, which range from 110 to 1835 m above MSL. It receives 1733 mm of mean precipitation annually and has 1219 mm of potential evapotranspiration (PET). The mean annual air temperature varies from 15 °C in winter to about 23 °C in summer depending on elevation. Umbric Dystruchrepts, Typic Dystruchrepts and Typic Udorthents are the major soil subgroups [33]. The dominant soil order of the study area is Inceptisols, followed by Entisols. The dominant land use and land covers are mixed dense forest, mixed open forest, grasslands, shifting cultivation and agricultural croplands.

2.2. Soil Sampling and Analysis

Grid-wise representative soil samples (0–25 cm depth) were collected during 2013 and 2014 (December 2013 to March 2014). The samples were collected at 1 km intervals in the north to south direction and at 2 km intervals in the east to west direction due to the difficult hilly terrain. The soil sampling exercise was part of one collaborative project between the ICAR-National Bureau of Soil Survey and Land Use Planning, Jorhat, Assam and the Department of Agriculture, Govt. of Nagaland, India. Each soil sample bag was tagged with the sample number, grid number and topographical sheet number mentioning the village and land use information. A total of 896 soil samples were collected in a rectangular fashion to cover the entire study area. The samples were dried in air under shade and stones and debris were removed. Dried samples were ground, sieved (2 mm sieve), and stored in a tagged polythene bottle for the analysis of soil properties and available nutrients in the laboratory of ICAR-National Bureau of Soil Survey and Land Use Planning, Jorhat, Assam.

The soil samples from grid points were analysed for pH, organic carbon, available macro- (N, P and K) and micronutrients (Fe, Mn, Zn and Cu) following standard procedures. The soil pH was measured in a 1:2.5 (w/v) soil–water suspension as per the standard procedure [34]. The soil organic carbon (OC) was analysed by the Walkley and Black method [35], available nitrogen (N) was determined by the alkaline KMnO₄ method [36], available phosphorus (P) by the Bray P-1 method [37] and the available potassium (K) was measured by the neutral normal NH₄OAc method [38] and then measured by a flame photometer (ELICO CL 361). The micronutrients were extracted by diethylene triamine penta-acetic acid [39] and measured using an atomic absorption spectrophotometer (Simadzu model No. AA-6300).

2.3. Environmental Covariates and Model Used

The ArcGIS 10 data management toolbox was used to process a DEM (30 m resolution) obtained from SRTM (https://earthexplorer.usgs.gov, accessed on 31 January 2022). Saga-GIS (6.3.0 version, University of Hamburg, Hamburg, Germany) was used to derive the data from the DEM, such as elevation, slope (Slp), slope height (SH), aspect (Asp), texture, convergence index (CI), valley depth (VD), channel network distance (CND), channel network base level (CNBL), convexity (CONV), normalized height (NH), standardized height (StH), mid-slope position (MSP), relative slope position (RSP), down-slope curvature (DC), local curvature (LC), local down-slope curvature (LDC), local upslope curvature (LUC), upslope curvature (UC), plan curvature (PlC) and profile curvature (PrC), LS factor, topographic ruggedness index (TRI), topographic wetness index (TWI), and topographic position index (TPI), multi-resolution ridge top flatness (MRRTF), multi-resolution index of valley bottom flatness (MRVBF) and total catchment area (TCA). The enhanced vegetation index (EVI) and the normalized difference vegetation index (NDVI) were employed (https://earthexplorer.usgs.gov, accessed on 31 January 2022) as variables to predict soil parameters in addition to DEM features (

Table 1. Variety of environmental covariates included in the model.

Predictor	Source	Resolution
Elevation	SRTM DEM	30 m
Slope (Slp)	SRTM DEM	30 m
Slope Height (SH)	SRTM DEM	30 m
Aspect (Asp)	SRTM DEM	30 m
Texture	SRTM DEM	30 m
Convergence Index (CI)	SRTM DEM	30 m
Valley Depth (VD)	SRTM DEM	30 m
Channel Network Distance (CND)	SRTM DEM	30 m
Channel Network Base Level (CNBL)	SRTM DEM	30 m
Convexity (CONV)	SRTM DEM	30 m
Standardized Height (StH)	SRTM DEM	30 m
Mid Slope Position (MSP)	SRTM DEM	30 m
Normalized Height (NH)	SRTM DEM	30 m
Relative Slope Position (RSP)	SRTM DEM	30 m
Down slope Curvature (DC)	SRTM DEM	30 m
Local Curvature (LC)	SRTM DEM	30 m
Local Down slope Curvature (LDC)	SRTM DEM	30 m
Local Upslope Curvature (LUC)	SRTM DEM	30 m
Upslope Curvature (UC)	SRTM DEM	30 m
Profile Curvature (PrC)	SRTM DEM	30 m
Plan Curvature (PlC)	SRTM DEM	30 m
Topographic Wetness Index (TWI)	SRTM DEM	30 m
Topographic Positioning Index (TPI)	SRTM DEM	30 m
Topographic Ruggedness Index (TRI)	SRTM DEM	30 m
LS-Factor	SRTM DEM	30 m
Multiresolution Index of Valley Bottom Flatness (MRVBF)	SRTM DEM	30 m
Multiresolution Index of the Ridge Top Flatness (MRRTF)	SRTM DEM	30 m
Total Catchment Area (TCA)	SRTM DEM	30 m
Enhanced Vegetation Index (EVI)	MOD13Q1v6.1 (2013–2014)	250 m, 16 days
Normalized Difference Vegetation Index (NDVI)	MOD13Q1v6.1 (2013–2014)	250 m, 16 days

). To predict the soil properties, environmental variables were extracted for all 896 sampling points. The descriptive statistics were computed for each soil property in R software [40]. For each soil property as well as elevation under consideration, Pearson’s correlation coefficient analysis was performed.

To analyse the relationship between the soil properties and environmental variables, stepwise multiple linear regression (SMLR) was used. Before performing regression, the soil properties were tested for normality, and the best normalization method found with respect to each soil property was used for data normalization. The standardized box cox transformation method was used for pH, OC, N and Fe, whereas Standardized Yeo-Johnson Transformation was conducted for P, Zn and Cu. Standardized asinh (x) Transformation and Order normal transformation was conducted in the case of K and Mn, respectively. The second step includes a spatial interpolation of the residuals using kriging. Before the semivariogram modelling and kriging, the residuals were tested for spatial dependency using the Moran’s I test. Then, the application of the regression model on the covariate raster was performed to generate the regression map; similarly, kriging maps of residuals were generated. The addition of a regression map and residual map followed by back-transformation resulted in a final regression kriged map of the predicted variables. The detailed framework of the regression kriging (RK) approach is available [41].

Validation was performed with the current available dataset (2019) in the study area (https://www.soilhealth.dac.gov.in, accessed on 31 January 2022) to evaluate the accuracy of the models, as well as to check the reliability of the data in order to generate valid MZs. In the study, different types of evaluation indices were used, such as coefficient of determination (R²), mean absolute error (MAE) and root mean square error (RMSE), to measure the accuracy of prediction [42].

$$MAE=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N\left|Z\left(x_i\right)-\widehat{Z\left(x_i\right)}\right|$$

(1)

where $\widehat{Z\left(x_i\right)}$ is the predicted value at location i. MAE has a direct relationship with error. The MAE measure does not disclose the magnitude of error that might occur at any point and, hence, RMSE was computed. The measure of RMSE has an inverse relationship with the accuracy of estimation, point-by-point.

$$RMSE=\sqrt{\frac{1}{N}{\sum }_{i=1}^N{\left[Z\left(x_i\right)-\widehat{Z\left(x_i\right)}\right]}^2}$$

(2)

2.4. Geographically Weighted Principal Components Analysis (GWPCA)

The predicted maps of soil properties generated using regression kriging were used for GWPCA. In global principal component analysis (GPCA), only a few components are used to explain the covariance structure of a multivariate dataset, and all of these are independent of location. GWPCA is a replacement for GPCA, where components depend on the location to capture spatial heterogeneity in a multivariate data structure in a geographical setting [43]. GWPCA has the ability to capture the influence of the original variable on each spatially varying component and change in spatial data dimensionality [28]. The covariance matrix for GW is calculated as follows:

$$\sum \left(u,v\right)={\mathrm{X}}^T{W}_{\left(u,v\right) }\mathrm{X}$$

(3)

where X is the data matrix with ‘n’ data points and ‘p’ covariates, and W_(u,v) is a ‘n’-dimensional symmetric diagonal distance weight matrix based on location (u,v) coordinates. Again, for each spatial location (u_i,v_i), the local eigenstructure under GWPCA setup defines as follows:

$$\mathrm{L}(u_i,v_i\left)\mathrm{V}\right(u_i,v_i){\mathrm{L}}^T(u_i,v_i)= \sum \left(u_i,v_i\right)$$

(4)

where L(u_i,v_i) is the eigenvector matrix and V(u_i,v_i) is a diagonal matrix based on eigenvalues, representing the variances of each principal component. Again, the score of each principal component ‘Z’ can be computed as:

$$\mathrm{Z}(u_i,v_i) = \mathrm{X}(u_i,v_i\left)\mathrm{L}\right(u_i,v_i)$$

(5)

From the summary statistics, it was evident that altitude had the maximum standard deviation (σ = 316.03), while pH had the lowest (σ = 0.38). To avoid variables with substantial variances from dominating the first major component of the data, a standardization technique was applied. Again, to prevent the effect of an outlier in the data, a robust GWPCA was adopted instead of a basic GWPCA based on the minimum covariance determinant (MCD) estimator [44]. The MCD estimator helped to select the best subset of data points (h) required for robust GWPCA based on its minimum value. The detailed procedure followed for robust GWPCA is as follows:

(1) 

Data were standardized and PCs were computed using the covariance matrix. The same GWPCA calibrations were performed using the same standardized data, which were similarly specified with (local) covariance matrices [45];

(2) 

As a rule of thumb, those components (such as k) were retained in GWPCA having eigenvalue ≥1, assuming the best representative of soil properties [46];

(3) 

Based on the minimum cross-validation score for the above-mentioned retained components, GWPCA determined the optimal bandwidth. A bi-square kernel function was used to provide an appropriate adaptive bandwidth for robust GWPCA analysis and to build a weighted matrix. The bi-square kernel function is calculated in the following way:

$$w_{ij}=\left\{\begin{array}{c}{\left(1-{\left(\frac{d_{ij}}{b}\right)}^2\right)}^{2 }if\left|d_{ij}\right|<b,\\ 0 otherwise\end{array}\right.$$

(6)

where ‘b’ is the bandwidth (geographical distance) and $d_{ij}$ is the spatial location distance between the ith and jth row in the data matrix.

(4) 

After the standardised data were translated into a spatial data frame, the robust GWPCA was conducted using the GW model of the ‘R package’ [47]. Outliers can artificially increase local variability and obfuscate crucial aspects in local data structures. Each local covariance matrix was estimated using the robust MCD estimator to generate a robust GWPCA [48]. From an array of h values (0.6 to 1), the MCD estimator finds the suitable “h” data points with the smallest sample covariance matrix;

(5) 

The GWPCA score was computed for “k” components for each location, which was subsequently used in the PFCM algorithm.

2.5. Possibilistic Fuzzy c-Means Algorithm (PFCM)

The PFCM was applied to the component scores of the GWPCA to partition the whole field into different distinct management zones (clusters). In order to produce distinct homogenous clusters by limiting within-cluster variability, the PFCM algorithm maximizes between-cluster variability. PFCM is a powerful algorithm and has been proposed to address the limitation of the fuzzy c-means (FCM) and possibilistic c-means (PCM) algorithms. The PFCM method solves FCM’s noise sensitivity-handling restriction as well as PCM’s limitation in the situation of coincidence clusters. This algorithm’s primary premise is to minimize the following objective function:

$$\underset{\left(U,T,V\right)}{\underbrace{min}}\left\{J\left(Z,U,T,V\right)={\sum }_{i=1}^C\sum _{k=1}^n\left(a{\mu }_{ik}^m+b{t}_{ik}^{\eta }\right)\parallel Z_k-V_i\parallel {}^{2 }+\sum _{i=1}^c{\gamma }_i\sum _{k=1}^n{\left(1-t_{ik}\right)}^{\eta }\right\}$$

(7)

Subject to the constraint ${\displaystyle \sum }_{i=1}^c{\mu }_{ik}=1 \forall k$ and ${\mu }_{ik}\ge 0,t_{ik}\le 1$. The user-specified constants b > 0, a > 0, η > 1, m > 1 and ${\gamma }_i>0$ are utilised here. The constants a and b define the proportional fraction of typicality and membership values. $U=\left[{\mu }_{ik}\right]$ is the membership matrix similar to FCM and $T=\left[t_{ik}\right]$ the typicality matrix similar to PCM. Z is the dataset, $Z_k=\left\{z_1,z_{2 },\dots ,z_n\right\}$ and the list of cluster centres is represented by $V_i=\left\{v_1,v_{2 },\dots ,v_c\right\}$. The different steps followed for the PFCM algorithm are given below:

(1) 

Decide on the number of clusters, e.g., “c”. The number of clusters in this study was initially set at a minimum of two and a maximum of 10;

(2) 

Distribute the cluster centroids at random. The study took into account a minimum of two centroids and a maximum of 10 centroids;

(3) 

The membership values of each data point for unique clusters were computed by minimising the following objective function:

$$\underset{\left(Z,U,V\right)}{\underbrace{min}}\left\{J\left(Z,U,V\right)={\sum }_{i=1}^C\sum _{k=1}^n{\mu }_{ik}^m\parallel Z_k-V_i\parallel {}^{2 }\right\}$$

(8)

(4) 

By using the previous step results, a suitable penalty parameter ${\gamma }_i$ for each cluster was assigned;

$${\gamma }_i=K\frac{{\sum }_{k=1}^n{\mu }_{ik}^m\parallel Z_k-V_i\parallel {}^{2 }}{{\sum }_{k=1}^n{\mu }_{ik}^m}$$

(9)

(5) 

The membership values were calculated, and $U=\left[{\mu }_{ik}\right]$ when the distance between the centroid and the data point exceeded 0;

$${\mu }_{ik}=\frac{1}{{\sum }_{j=1}^c{\left(\frac{\parallel Z_k-V_i\parallel }{\parallel Z_k-V_j\parallel }\right)}^{\frac{2}{m-1}}}$$

(10)

(6) 

When the data point’s distance from the centroid was more than 0, $T=\left[t_{ik}\right]$ was used to determine the typicality values;

$$t_{ik}=\frac{1}{1+{\left(\frac{b}{\eta }\parallel Z_k-V_i\parallel {}^2\right)}^{\frac{1}{\left(\eta -1\right)}}}$$

(11)

(7) 

The centre vector “v_i” was calculated using:

$$v_i=\frac{{\sum }_{k=1}^n\left(a{\mu }_{ik}^m+b{t}_{ik}^{\eta }\right)Z^k}{{\sum }_{k=1}^n\left(a{\mu }_{ik}^m+b{t}_{ik}^{\eta }\right)}$$

(12)

(8) 

Stop when the error is less than $\delta$ ($\parallel V_{k+1}-V_k<\parallel \delta$), if not, go to step 6.

The PFCM was carried out in this investigation using the R package “ppclust” [49]. The default parameter settings provided in “ppclust” were used for a, b and η. The following parameters were set: fuzziness exponent (m) = 1.5; convergence criteria ($\delta$) = 0.0001; and the minimum and the maximum number of clusters, respectively, were 2 and 10. The optimum number of clusters was decided based on the two most powerful cluster validation indexes, such as the fuzzy performance index (FPI) [50] and normalized classification entropy (NCE) [51], which are defined as follows:

$$\mathrm{FPI}=1-\frac{c}{c-1}\left[1-\frac{{{\displaystyle \sum }}_{i=1}^c{{\displaystyle \sum }}_{k=1}^n{\left({\mu }_{ik}\right)}^2}{n}\right]$$

(13)

$$\mathrm{NCE}=\frac{n}{n-c}\left[-\frac{{{\displaystyle \sum }}_{k=1}^n{{\displaystyle \sum }}_{i=1}^c{\mu }_{ik{\log }_a\left({\mu }_{ik}\right)}}{n}\right]$$

(14)

where μ_ik defines the fuzzy membership of each observation. The letters c and n stand for the number of clusters and observations, respectively. The FPI calculates the degree of fuzziness of a particular number of clusters and it varies from 0 to 1. The number ‘0’ suggests crisp/distinct clusters with low membership sharing, but values approaching 1 imply no separate clusters due to a high degree of observation membership sharing among multiple clusters. The NCE value indicates the degree of disorganization generated by a set of classes. The best number of clusters was determined by the lowest value of both the FPI and NCE indexes, which indicated the least amount of members sharing and the most organization in data portioning [52]. Furthermore, to evaluate the heterogeneity among various MZs, an analysis of variance followed by Tukey’s HSD test was used to validate the reliability of distinct MZs. In the current study, all statistical analysis was performed using R software. The methodology adopted in the present study is illustrated in Figure 2.

3. Results

3.1. Variability of Soil Properties and Available Nutrients

The soil reaction (pH) ranged from 3.60 to 6.50, which is extremely acid to slightly acid in nature (

Table 2. Descriptive statistics of soil properties in India’s north-eastern Himalayan area.

Soil Properties	Mean	Min.	Max.	Median	CV (%)	SD	SE	Skewness	Kurtosis
Altitude (m)	597.48	100.00	1835.00	567.50	52	316.03	10.56	0.57	−0.24
pH	4.56	3.60	6.50	4.5	8.39	0.38	0.01	0.93	2.05
OC	2.19	0.19	5.12	2.04	42.7	0.93	0.03	0.31	−0.53
N	427	50.8	997	410	36.6	156	5.22	1.21	4.13
P	44.7	21.8	118	39.7	38.9	17.4	0.58	5.00	61.4
K	306	67.0	996	271	51.0	156	5.22	1.43	2.70
Fe	61.6	0.51	143	62.4	38.8	23.9	0.80	0.15	0.05
Mn	27.5	0.03	96.9	22.2	71.2	19.5	0.65	0.80	−0.09
Zn	1.40	0.01	7.70	1.03	83.2	1.16	0.04	2.30	6.43
Cu	0.90	0.07	16.6	0.75	84.0	0.75	0.03	10.81	212

OC, soil organic carbon (%); N, available nitrogen (kg ha⁻¹); P, available phosphorus (kg ha⁻¹); K, available potassium (kg ha⁻¹); Fe, Mn, Zn and Cu represent DTPA-extractable iron, manganese, zinc and copper in soil (mg kg⁻¹), respectively; CV, coefficient of variation; SD, standard deviation; SE, standard error.

).

The mean N (ranging from 50.8 to 997 kg ha⁻¹), P (ranging from 21.8 to 118 kg ha⁻¹) and K (ranging from 67 to 996 kg ha⁻¹) values were medium to high, with values of 427, 44.7 and 306 kg ha⁻¹, respectively. The mean values of Fe, Mn, Zn and Cu in this region were 61.6, 27.5, 1.40 and 0.90 mg kg⁻¹, respectively, and their concentrations varied widely. The CV values of macronutrients were moderate, ranging from 37% for N to 51% for K. As compared to macronutrients, the micronutrients’ CV values were high (71% for Mn to 84% for Cu), except for Fe (39%).

3.2. Relationship between Soil Characteristics and Nutrient Availability

The correlation matrix showed that almost all of the soil chemical properties, except N, were significantly correlated with each other (

Table 3. Correlation matrix for soil properties in India’s north-eastern Himalayan area.

	pH	OC	N	P	K	Fe	Mn	Zn	Cu	Altitude
pH	1.00
OC	−0.01	1.00
N	−0.05	0.53 b	1.00
P	0.33 b	0.03	0.12 b	1.00
K	0.41 b	0.28 b	0.23 b	0.38 b	1.00
Fe	−0.08 b	0.25 b	0.22 b	0.14 b	0.03	1.00
Mn	0.30 b	0.18 b	0.19 b	0.24 b	0.41 b	0.15 b	1.00
Zn	0.18 b	0.15 b	0.20 b	0.25 b	0.35 b	0.31 b	0.49 b	1.00
Cu	0.03 a	0.04	0.09 b	−0.01	0.12 b	0.12 b	0.17 b	0.33 b	1.00
Altitude	0.09 b	0.45 b	0.34	0.06 b	0.21	0.01 b	0.18 a	0.07	0.04 b	1.00

OC, soil organic carbon; N, available nitrogen; P, available phosphorus; K, available potassium; Fe, Mn, Zn and Cu represent DTPA-extractable iron, manganese, zinc and copper in soil, respectively. ^a Correlation is significant at the 0.05 level; ^b Correlation is significant at the 0.01 level.

). N, OC and Fe were negatively correlated with the soil pH, whereas Cu, Zn, Mn, K and P were positively affected. Increases in soil pH within this range (3.6 to 6.5) resulted in lower N and Fe concentrations and higher K, P, Mn, Zn and Cu concentrations in these soils, according to our findings.

3.3. Spatial Nature of Soil Properties and Available Nutrients

Attention was paid to surface soil properties, such as pH, OC, available N, P, K, Fe, Mn, Zn and Cu.

Table 4. Results of the stepwise multiple linear regression model relating soil properties to environmental covariates.

Variable	Significant Predictors	Intercept	R-Squared	p-Value
pH	−1.12 + 0.023 × CONV − 0.001 × SH + 0.0002 × CNBL	Significant	0.07	0.03969
OC	−1.43 + 0.002 × CNBL + 0.13 × LDC + 0.22 × NH + 1.22 × Slp − 0.04 TRI	Significant	0.26	2.2 × 10−16
N	−1.26 − 0.001 × CND + 0.001 × Elevation + 0.001 × VD	Significant	0.16	2.2 × 10−16
P	−0.04 + 0.002 × RSP − 0.59 × CND	Significant	0.12	0.04261
K	−0.78 + 0.001 × CNBL + 0.54 × NH − 0.0006 × StH + 0.0005 × VD	Significant	0.09	1.201 × 10−8
Fe	−0.14 × CNBL − 0.035 × CND − 0.4 × DC − 0.24 × LUC + 0.32 × MSP − 0.44 × SH + 0.03 × Elevation + 0.04 × TPI + 0.02 × TRI	Significant	0.08	0.001885
Mn	−0.45 + 0.03 × CNBL + 0.03 × CND + 0.16 × DC − 0.18 × LDC − 1.38 × RSP	Significant	0.10	7.922 × 10−7
Zn	−0.22 + 0.0005 × CNBL + 0.002 × CND − 1 × RSP	Significant	0.06	0.0002717
Cu	1.05 + 0.04 × Asp − 0.003 × CNBL − 0.02 × CONV − 1.25 × LDC − 1.84 × LUC − 1.04 × RSP + 0.0037 × Elevation	Significant	0.11	7.02 × 10−6

presents the best predictor (environmental covariates) identified through the SMLR model. The SMLR model for OC and available N had R² (coefficient of determination) values of 0.26 and 0.16, respectively, showing moderate prediction power. Meanwhile, for the others, the R² showed a poor correlation between the predicted variables and the predictors. However, the p-values for each variable were significant.

The prediction residuals obtained through semivariogram analysis are shown in Figure 3. The residuals of Zn showed a strong spatial correlation with a percent nugget of 11% and a range of 5738 m with the Gaussian model. Moderate spatial correlation was shown in the case of OC (percent nugget of 70% and range of 5369 m; Gaussian model), P (percent nugget of 69% and range of 4108 m; Circular model) and K (percent nugget of 74% and range of 2259 m; Exponential model). The residuals of pH, N, Fe, Mn and Cu had high percent nugget (81–87%) with varied ranges (4321–10,260 m) because of a nugget effect (

Table 5. Semivariogram parameters of soil property residuals in India’s north-eastern Himalayan area.

Variable	Model	Nugget	Partial Sill	Sill	Nugget/Sill	Nugget/Sill (%)	Range (m)	Moran’s I Test Value	p-Value	Spatial Autocorrelation	Spatial Dependence
pH	Circular	0.818	0.188	1.006	0.81	81	6443	0.042215	<0.001	Present	Weak
OC	Gaussian	0.560	0.243	0.803	0.70	70	5369	0.022289	<0.001	Present	Moderate
N	Gaussian	0.765	0.112	0.877	0.87	87	10260	0.019618	<0.001	Present	Weak
P	Circular	0.696	0.312	1.008	0.69	69	4108	0.016005	<0.001	Present	Moderate
K	Exponential	0.687	0.244	0.931	0.74	74	2259	0.020067	<0.001	Present	Moderate
Fe	Gaussian	0.789	0.172	0.961	0.82	82	4321	0.017918	<0.001	Present	Weak
Mn	Circular	0.790	0.176	0.966	0.82	82	6777	0.014049	<0.001	Present	Weak
Zn	Gaussian	0.108	0.851	0.959	0.11	11	5738	0.020812	<0.001	Present	Strong
Cu	Circular	0.795	0.189	0.984	0.81	81	7846	0.02022	<0.001	Present	Weak

OC, soil organic carbon; N, available nitrogen; P, available phosphorus; K, available potassium; Fe, Mn, Zn and Cu represent DTPA-extractable iron, manganese, zinc and copper in soil, respectively.

).

The performance of the stepwise multiple linear regression equation was evaluated. The validation with respect to the current dataset (Figure 4) demonstrated that combining diverse variables improved the variability of the predicted soil parameters viz., pH, organic carbon, available N, P, K, Fe, Mn, Zn and Cu. Medium to high variability was captured by the model (R² = 0.32–0.81). The highest variability was captured in the case of N (0.81) followed by pH (0.76), OC (0.71), P (0.67), Cu (0.45), K (0.42), Fe (0.34), Mn (0.33) and Zn (0.32).

The predicted maps of the studied soil properties (pH, OC, available N, P, K, Fe, Mn, Zn and Cu) in the surface soil using stepwise multiple regression kriging are presented in Figure 5. The predicted soil reaction (pH) varied from 4–5 and soil organic carbon varied from 0.4 to 3.7. The predicted macronutrients viz., N, P and K varied from 268.9 to 652.8 kg ha⁻¹, 31 to 78.8 kg ha⁻¹ and 112.6 to 139.0 kg ha⁻¹, respectively. Similarly, in the case of available micronutrients viz. Fe, Mn, Zn and Cu, the predicted maps varied from 7.9 to 139.0 mg kg⁻¹, 4.0 to 77.2 mg kg⁻¹, 0.4 to 2.9 mg kg⁻¹ and 0.1 to 2.3 mg kg⁻¹, respectively.

3.4. Delineation of Management Zones

The projected soil parameters for the entire region were used to define the management zones. The soil properties were predicted for each pixel value (total 17, 86,985 data points) using the model described in the previous section. To gain a better understanding of the geographically weighted model output, in this study, the usual global model was fit, which excludes the spatial effect. Therefore, a PCA was conducted on the predicted variables (regression kriging), such as the soil properties, and available nutrients. The first three PCs explained the cumulative percentage of the total variance (PTV) as 67.7% having eigenvalues greater than one (

Table 6. Soil properties and loading coefficients: global principal component analysis.

Principal Component	Eigenvalues	Proportion of the Total Variance (PTV)				Cumulative PTV
PC1	1.707	0.338				0.338
PC2	1.275	0.189				0.527
PC3	1.137	0.150				0.677
PC4	0.855	0.085				0.762
PC5	0.814	0.077				0.839
PC6	0.739	0.063				0.902
PC7	0.623	0.045				0.947
PC8	0.525	0.032				0.979
PC9	0.425	0.021				1.000
	PC loading
	pH	OC	N	P	K	Cu	Zn	Mn	Fe
PC1	−0.141	−0.502	−0.436	−0.066	−0.404	−0.167	−0.391	−0.394	−0.187
PC2	0.432	−0.262	−0.436	0.509	−0.063	−0.064	0.291	0.185	0.410
PC3	−0.348	0.051	0.006	−0.121	−0.413	0.580	0.192	−0.190	0.531

OC, soil organic carbon; N, available nitrogen; P, available phosphorus; K, available potassium; Fe, Mn, Zn and Cu represent DTPA-extractable iron, manganese, zinc and copper in soils, respectively.

).

The variance explained by PC1, PC2 and PC3 was 33.8, 18.9 and 15.0%, respectively. The most significant influence was found for OC, N, K and Mn in PC1. In PC2, P, pH and Fe contributed more. Likewise, in PC3, Cu had the most significant influence. As a result, the distribution maps for OC and N were found to have similarity to the GPCA scores map of PC1. The PC2 and PC3 score maps were identical to the Cu, Fe and Mn maps. However, the PCA combined nine variables into three PCs, accounting for gross spatial variability in these variables. High negative scores were concentrated in the south-eastern part of the study area, whereas large positive scores were concentrated in the northern and central parts (Figure 6), with no discernible geographical trend. All soil samples described 92.05 to 98.47% of the data variability, with an average of 95.78%, explaining 28.08% more variability than GPCA (67.7%). In the spatial data structure, GWPCA was a clear winner over GPCA. When PCAs explained more variability, they observed the soil nutrient properties of different samples with more clarity. Further, these PCAs were used for the computation of the PCA score, which was an input for possibilistic fuzzy c-means clustering in the final MZs decision. When the data showed more variability, they indirectly enhanced the crisp clustering of soil samples, which is the objective of this study.

For management zone analysis, the first three PCs’ scores of GWPCA and GPCA were used as inputs separately in the “ppclust” package of R to perform the PFCM algorithm to segregate the three PCs into MZs. For 2 to 10 MZs, the method was repeated numerous times to obtain cluster validity indices. The cluster validity indices (FPI and NCE) were plotted against the number of classes on a graph (Figure 7). As a consequence of clustering, the optimal number of clusters was determined when each index reached the lowest value, signalling minimal membership sharing (FPI) or highest amount of organization (NCE). Thus, it was found that, for both methods of data redundancy, the number of reasonable clusters was four.

3.5. Comparison of Delineated Zones

The characterization of the variability with respect to space while considering both methods, i.e., GPCA and GWPCA, for the delineated MZs was conducted using Tukey’s multiple comparison test (

Table 7. Variance analysis of soil properties in management zones and Tukey multiple comparisons test based on the GPCA score and GWPCA score in India’s north-eastern Himalayan area.

Soil Properties	PFCM Clustering Based on GPCA Score				PFCM Clustering Based on GWPCA Score
	1	2	3	4	1	2	3	4
pH	4.50 c	4.66 a	4.50 c	4.50 b	4.53 b	4.54 a	4.52 d	4.53 c
OC	1.99 c	2.12 b	2.13 b	3.06 a	2.28 a	2.11 d	2.15 c	2.18 b
N	402.81 b	380.37 d	387.95 c	513.14 a	408.25 b	394.91 c	413.59 a	406.73 b
P2O5	39.88 c	45.66 a	39.96 b	38.07 d	41.46 a	40.59 c	40.13 d	40.83 b
K2O	272.84 c	306.38 a	255.17 d	295.29 b	284.81 a	265.97 d	273.01 b	270.79 c
Fe	54.24 d	63.96 b	64.47 a	61.30 c	62.33 a	60.10 b	58.70 c	60.12 b
Mn	20.15 c	30.05 a	21.89 b	29.93 a	24.91 a	22.61 d	23.92 b	23.26 c
Zn	0.94 c	1.19 a	1.09 b	1.09 b	1.09 a	1.06 c	1.02 d	1.06 b
Cu	0.69 c	0.69 c	0.76 b	0.77 a	0.74 a	0.73 b	0.71 d	0.72 c

p ≤ 0.01 indicates that values in a row followed by different letters are significantly different. OC, soil organic carbon; N, available nitrogen; P, available phosphorus; K, available potassium; Fe, Mn, Zn and Cu represent DTPA-extractable iron, manganese, zinc and copper in soils, respectively.

); it was observed that the PFCM clustering based on GWPCA was found to be superior to PFCM clustering based on GPCA. Therefore, by considering the pixel-wise cluster values resulting from the PFCM clustering based on GWPCA, the final MZs map was generated using R software (Figure 8).

MZ 1 covered the maximum area (43.3%), followed by MZ 2 (29.4%), MZ 3 (27.0%) and MZ 4 (0.3%). The analysis of variance indicated significant differences among MZs with reference to all soil properties, except for N and Fe. There were no significant differences between MZ 1 and MZ 4 in the case of N, and, similarly, no significant differences between MZ 2 and MZ 4 in the case of Fe.

4. Discussion

It is indeed critical to monitor the nutrient level of soil on a regular basis. In such rugged terrain, timely surveying is a difficult and costly task. In light of the foregoing, samples gathered in the research region were analysed to determine the relationship with environmental variables and then segregated to create a reasonable number of management zones that can be controlled. In this study, it was found that the soil properties were quite variable, with a significant coefficient of variance. The OC content was high in the soils of Nagaland state due to thick vegetation cover [53]. Forest diversity, geographical factors, and climate change impacts have all been linked to the higher OC in this region [54]. The soil’s physical and chemical characteristics and alterations in the quality and quantity of organic matter input into the soils are being primarily influenced by the mean annual temperature, hence regulating the OC stability [55]. The variation in the concentration of available nutrients may be attributed to prevailing climatic conditions, contrasting landforms, parent materials and dynamic land-use patterns [56,57,58]. The studied soil properties showed low to very high variability. Out of all of the soil properties, the lowest CV value was registered by the pH. Several authors have documented modest and moderate variations in the soil pH and OC concentration in India’s acid soils, which are consistent with our findings [16,57,59].

The substantial diversity in soil micronutrient availability throughout space might be due to changes in parent materials and paedogenic processes, which are the two major causes of variance [60]. The high CV values of soil parameters indicated spatial variability, which pushed for site-specific fertilizer management to boost crop output.

A correlation study suggested that variations in soil pH are causing changes in micronutrient solubility and distribution [39]. Tripathi et al. [59] also reported the positive correlation between the soil pH and available Zn and Mn in the rice cultivation soils of Odisha. In addition to these, the micronutrients were positively and substantially connected with each other, and there was a positive and significant link between OC and accessible Fe, Mn, Zn and Cu. The present results corroborated the findings of others [61,62].

It was observed in the case of the SMLR model in the present study that the prediction power was moderate for OC and N, but low prediction was observed for other soil attributes with a significant contribution of covariates in the model. In comparison to previous research, the outcomes differ depending on the models employed, the projected soil properties, and the study’s location. Mapping macronutrients in agricultural (depth 0–15 cm) lands in Iran with the cubist model yielded a lower validation R² of 13% for N, but a higher, though still low, R² of 17% for P, compared to the current work [63]. With the QRF in the semiarid tropics of South India at a 30 cm depth, Dharumarajan et al. [64] obtained substantially lower R² values of 0.23 for OC. In the prediction of soil parameters, factors such as the sampling intensity in relation to the geographical extent, topography features and bioclimatic variables may have played a critical impact. The soil characteristics displayed a pattern of spatial dependency that might be attributable to internal variables, such as chemical, physical and mineralogical features, external influences, such as human activities, or both [24,65]. The pH and OC ranges in the research region were moderate. Reza et al. [66] found a similar pH range in the alluvial soils of India; however, Fathi et al. [67] found a smaller range of pH and organic matter variability. The influence zones for N, P and K were arranged in decreasing order. It was relatively high for N, but not so much for P or K. Reza et al. [68] showed a similar and larger geographical range for available N (2.0 km) and available K (2.3 km) at the district level of soil fertility mapping. When considering the zone of effect at the district level, the trend in soil micronutrients was moderate. While using kriging interpolation approaches, some authors observed varying micronutrient ranges [69,70,71]. The effect of random factors and the resolution of gridded soil data might explain these contradicting results in terms of the spatial range of soil attributes. Apart from the spatial range, another key indication is spatial dependency. The soil pH, N, Fe, Mn and Cu had modest spatial dependence, but OC, P and K had moderate geographical dependence, except for Zn, which had large geographical dependence. This is due to topography, prevailing climate conditions, soil types and changing land-use patterns, such as shifting farming. In the research region, around 101 km² of land was subjected to intermittent shifting cropping [72].

The soil properties showed high variations in the spatially predicted maps, which were ascribed to the changing nature of the environment, land use and management [12]. Such predicted maps with high spatial resolution are necessary for assessing and monitoring soil health and, at the same time, they will act as a guide for developing a proper land-use plan.

The methodology of delineation of MZs solely considered the available nutrients, but the abeyance of spatial information in PCA does not justify our hypothesis concerning the segregation of distinct MZs. Distinct spatial variation was observed in the maps of soil characteristics; however, it is impossible to identify the variables responsible for regional variations. In terms of variance decomposition for spatial data sets, the use of a GPCA in a spatial data structure provides an incomplete view. GPCA does not consider the local structure (i.e., longitude/latitude) of soil nutrients, which tends to provide an incomplete understanding of soil nutrient distribution over space. To avoid such problems, GWPCA was used to adopt a local distribution pattern of soil nutrients over space, which is essential for the delineation of MZs. GWPCA is nothing but the local adaptation of classical PCA in a spatial data structure.

Considering the additional advantages of the former, the anticipated spatial heterogeneity in the soil properties and available nutrients was due to the GWPCA. The results from GWPCA and GPCA were compared throughout. The comparison between GWPCA and GPCA was conducted for the first three components from each calibration and the PC scores were mapped (PC1 to PC3) (Figure 6). For GWPCA, the total n = 17, 86 and 985 valued scores dataset (raster data) was generated through regression kriging for each location, i.e., 30 m spatial resolution of each component. In GWPCA, there were 17, 86 and 985 PCAs (corresponding to each pixel) for each soil nutrient in comparison to GPCA, where only one PCA existed for each nutrient. As a result, the GWPCA scores corresponding to their location were computed. A matrix of three main components (eigenvalue ≥ 1) was chosen for each site, together with their corresponding amount of variance explained and the winning variables for downstream analysis. The best bandwidth (bw) was calculated by using a bi-square method for k = 3 components based on the minimum CV, and was found to be bw = 1, 10, 207. A sample of h = 0.85 n (n = 17, 86, 985) data points was chosen based on the shortest MCD estimator for robust GWPCA estimation [73]. It was clear that the MZs generated through the former procedures were evidently (based on analysis of variance) different from each other (Table 7) [14,59,74].

Variations in mineralogy, microclimatic variables, and other anthropogenic activities, such as soil and crop management, may account for the differences across the four MZs [13,57]. The study area is located on the western slope of the Purvanchal hills of the north-eastern Himalayan region, where the elevation decreases from east to west and the climate, vegetation and parent material vary significantly with elevation, from warm to humid thermic ecosystems at higher elevations to the hot moist sub-humid hyperthermic ecosystem at lower elevations. As a result, the altitude was a component that contributed to the variation in soil properties. Greater mean amounts of these nutrients might be linked to higher levels of OC, acidic pH, high altitude with temperature changes and forest vegetation, notwithstanding the substantial diversity across the MZs. Especially in the case of micronutrients, several authors also reported that the availability of micronutrients in the acidic and highly weathered soils of the north-eastern hilly regions are quite high [20,21,22,75,76]. Only 2.11% of the study area is covered by agriculture, with the majority of the land covered by various forest vegetation (87.93%), followed by other land cover classifications. The main source of concern in the district, which covers 6.31% of the total land area, is shifting agriculture [72]. This zonation concept based on essential nutrient availability combined with the land use–land cover layer will aid in identifying suitable areas for growing cereals, pulses, vegetables and tuber crops through judicious nutrient applications, as previous studies have suggested land use planning based on pedological attributes, rather than considering soil fertility parameters. The method would also provide an effective and efficient means for scientific nutrient management. The above study on geostatistical analysis illustrated the regional heterogeneity of soil properties in terms of spatial dependency, especially macro and micronutrients. As a result, knowledge of soil qualities in individual MZs might be valuable for farmers and other stakeholders to make informed decisions about nutrient management on a site-by-site basis.

5. Conclusions

The current work used geospatial modelling to propagate regional variation in soil characteristics and available nutrients in the NEHR, which was then translated into MZs using GWPCA and probabilistic fuzzy clustering techniques. The latter demonstrates the benefits of GWPCA over normal GPCA, since GWPCA provides information on the geographical distribution of variance and the factors that have the greatest effect on each component, whereas GPCA suppressed such information. Since it is doubtful that all of the yield-limiting parameters are known ahead of time, MZs produced by a set of characteristics are more likely to characterize the complex regional variation of soil fertility. Indeed, various variables may impact fertility in different regions of the same field. The regression kriging model predicted the soil properties and available nutrients reasonably well. The prediction of soil properties and available nutrients by the present model was good, except for N, Zn and Cu. The GWPCA and fuzzy clustering by considering predicted soil properties had segregated the study area into four MZs, which indicated the heterogeneity in the soil properties among them. MZ maps created with these approaches are simple, easy to comprehend and cost-effective, and might be used as key guidance for farmers when it comes to site-specific fertilizer management. As information on conventional fertilizer dosage recommendations is scarce in this region, the mean values of soil characteristics in each MZ can be utilized as a reference for variable-rate fertilization and liming. Therefore, fuzzy cluster analysis would minimize variability within the zone and would provide an effective and efficient means for various interventions for the agricultural purpose, not only in this region, but also elsewhere. Further research should concentrate on the inclusion of more covariates viz., climatic data, geological and other remote sensing information to enhance the prediction and to monitor the effect of temporal changes of nutrients on soil and crop management practices.