Assessing the Relationship between Freshwater Flux and Sea Surface Salinity
Abstract
:1. Introduction
2. Data and Methods
2.1. Precipitation Datasets
2.1.1. GPCP v3.1
2.1.2. CMAP
2.1.3. CMORPH
2.1.4. GPM IMERG
2.1.5. PERSIANN CDR
2.1.6. TRMM 3B42
2.1.7. MSWEP
2.2. Evaporation Datasets
2.2.1. OAFlux
2.2.2. IFREMER
2.2.3. J-OFURO3
2.2.4. SEAFLUX
2.3. SSS Datasets
2.3.1. SMOS BEC
2.3.2. SMOS CEC
2.3.3. ESA CCI
2.3.4. OISSS
2.3.5. CMEMS
2.4. MLD Dataset
2.5. Methods
2.5.1. Calculation for Evaporation
2.5.2. Calculation for Statistical Properties
2.5.3. Preparation for Calculating SSS Tendency and Freshwater Flux
3. Results
3.1. Intercomparison among E and P
3.2. Intercomparison in SSS Datasets
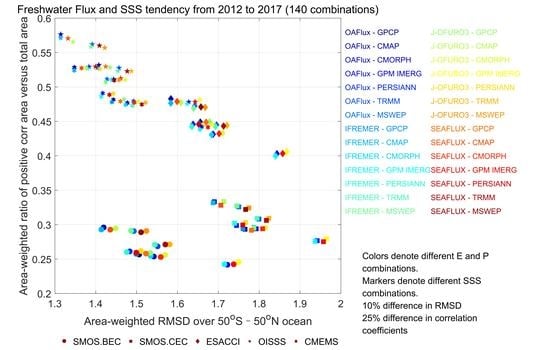
3.3. Relationship between Satellite-Based EMP and SSS Tendency
4. Discussion
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bingham, F.M.; Foltz, G.; McPhaden, M. Characteristics of the seasonal cycle of surface layer salinity in the global ocean. Ocean Sci. 2012, 8, 915–929. [Google Scholar] [CrossRef] [Green Version]
- Elliott, G.W. Precipitation signatures in sea-surface-layer conditions during BOMEX. J. Phys. Oceanogr. 1974, 4, 498–501. [Google Scholar] [CrossRef] [Green Version]
- Durack, P.J.; Wijffels, S.E. Fifty-year trends in global ocean salinities and their relationship to broad-scale warming. J. Clim. 2010, 23, 4342–4362. [Google Scholar] [CrossRef]
- Helm, K.P.; Bindoff, N.L.; Church, J.A. Changes in the global hydrological-cycle inferred from ocean salinity. Geophys. Res. Lett. 2010, 37, L18701. [Google Scholar] [CrossRef]
- Lago, V.; Wijffels, S.E.; Durack, P.J.; Church, J.A.; Bindoff, N.L.; Marsland, S.J. Simulating the role of surface forcing on observed multidecadal upper ocean salinity changes. J. Clim. 2015, 29, 5575–5588. [Google Scholar] [CrossRef]
- Baumgartner, A.; Reichel, E. The World Water Balance: Mean Annual Global, Continental and Maritime Precipitation and Run-Off; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Durack, P.J.; Wijffels, S.E.; Matear, R.J. Ocean salinities reveal strong global water cycle intensification during 1950 to 2000. Science 2012, 336, 455–458. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dorigo, W.; Dietrich, S.; Aires, F.; Brocca, L.; Carter, S.; Cretaux, J.-F.; Dunkerley, D.; Enomoto, H.; Forsberg, R.; Güntner, A.; et al. Closing the Water Cycle from Observations across Scales: Where Do We Stand? Bull. Am. Meteorol. Soc. 2021, 102, E1897–E1935. [Google Scholar] [CrossRef]
- Hosoda, S.; Suga, T.; Shikama, N.; Mizuno, K. Global surface layer salinity change detected by Argo and its implication for hydrological cycle intensification. J. Oceanogr. 2009, 65, 579–586. [Google Scholar] [CrossRef]
- Terray, L.; Corre, L.; Cravatte, S.; Delcroix, T.; Reverdin, G.; Ribes, A. Near-surface salinity as nature's rain gauge to detect human influence on the tropical water cycle. J. Clim. 2012, 25, 958–977. [Google Scholar] [CrossRef] [Green Version]
- Yu, L. A global relationship between the ocean water cycle and near-surface salinity. J. Geophys. Res. Ocean. 2011, 116, C10025. [Google Scholar] [CrossRef]
- Vinogradova, N.T.; Ponte, R.M. Clarifying the link between surface salinity and freshwater fluxes on monthly to interannual time scales. J. Geophys. Res. Ocean 2013, 118, 3190–3201. [Google Scholar] [CrossRef]
- Vinogradova, N.T.; Ponte, R.M. In Search of Fingerprints of the Recent Intensification of the Ocean Water Cycle. J. Clim. 2017, 30, 5513–5528. [Google Scholar] [CrossRef]
- Ponte, R.; Vinogradova, N. An assessment of basic processes controlling mean surface salinity over the global ocean. Geophys. Res. Lett. 2016, 43, 7052–7058. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Jin, X.; Josey, S.A.; Lee, T.; Kumar, A.; Wen, C.; Xue, Y. The Global Ocean Water Cycle in Atmospheric Reanalysis, Satellite, and Ocean Salinity. J. Clim. 2017, 30, 3829–3852. [Google Scholar] [CrossRef]
- Grodsky, S.A.; Carton, J.A. Delayed and Quasi-Synchronous Response of Tropical Atlantic Surface Salinity to Rainfall. J. Geophys. Res. Ocean. 2018, 123, 5971–5985. [Google Scholar] [CrossRef]
- Tzortzi, E. Sea Surface Salinity in the Atlantic Ocean from the SMOS Mission and Its Relation to Freshwater Fluxes. Ph.D. Thesis, University of Southampton, Southampton, UK, 2015. [Google Scholar]
- Yueh, S.H.; West, R.; Wilson, W.J.; Li, F.K.; Njoku, E.G.; Rahmat-Samii, Y. Error sources and feasibility for microwave remote sensing of ocean surface salinity. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1049–1060. [Google Scholar] [CrossRef] [Green Version]
- Henocq, C.; Boutin, J.; Reverdin, G.; Petitcolin, F.; Arnault, S.; Lattes, P. Vertical Variability of Near-Surface Salinity in the Tropics: Consequences for L-Band Radiometer Calibration and Validation. J. Atmos. Ocean. Technol. 2010, 27, 192–209. [Google Scholar] [CrossRef]
- Boutin, J.; Chao, Y.; Asher, W.E.; Delcroix, T.; Drucker, R.; Drushka, K.; Kolodziejczyk, N.; Lee, T.; Reul, N.; Reverdin, G. Satellite and in situ salinity: Understanding near-surface stratification and subfootprint variability. Bull. Am. Meteorol. Soc. 2016, 97, 1391–1407. [Google Scholar] [CrossRef] [Green Version]
- Stammer, D.; Martins, M.S.; Köhler, J.; Köhl, A. How well do we know ocean salinity and its changes? Prog. Oceanogr 2021, 190, 102478. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Huffman, G.J.; Behrangi, A.; Bolvin, D.T.; Nelkin, E.J. (Eds.) GPCP Version 3.1 Satellite-Gauge (SG) Combined Precipitation Data Set; NASA GES DISC: Greenbelt, MD, USA, 2020. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Keehn, P.R. Global tropical rain estimates from microwave-adjusted geosynchronous IR data. Remote Sens. Rev. 1994, 11, 125–152. [Google Scholar] [CrossRef]
- Susskind, J.; Piraino, P.; Rokke, L.; Iredell, L.; Mehta, A. Characteristics of the TOVS Pathfinder Path A dataset. Bull. Am. Meteorol. Soc. 1997, 78, 1449–1472. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Hsu, K.; Kidd, C.; Nelkin, E.J.; Tan, J.; Xie, P. Algorithm Theoretical Basis Document (ATBD) for Global Precipitation Climatology Project Version 3.0 Precipitation Data; MEaSUREs project: Greenbelt, MD, USA, 2019. [Google Scholar]
- Xie, P.; Arkin, P.A. Global Precipitation: A 17-Year Monthly Analysis Based on Gauge Observations, Satellite Estimates, and Numerical Model Outputs. Bull. Am. Meteorol. Soc. 1997, 78, 2539–2558. [Google Scholar] [CrossRef]
- Xie, P.; Joyce, R.; Wu, S.; Yoo, S.; Yarosh, Y.; Sun, F.; Lin, R. NOAA Climate Data Record (CDR) of CPC Morphing Technique (CMORPH) High Resolution Global Precipitation Estimates, Version 1; RDA/UCAR: Research Data Archive at the National Center for Atmospheric Research; Computational and Information Systems Laboratory, National Centers for Environmental Information, NESDIS, NOAA: Greenbelt, MD, USA, 2020. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. GPM IMERG Final Precipitation L3 1 Month 0.1 Degree x 0.1 Degree V06; Goddard Earth Sciences Data and Information Services Center: Greenbelt, MD, USA, 2019. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; Van Dijk, A.I.; McVicar, T.R.; Adler, R.F. MSWEP V2 global 3-hourly 0.1 precipitation: Methodology and quantitative assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Weller, R.A. Objectively Analyzed Air–Sea Heat Fluxes for the Global Ice-Free Oceans (1981–2005). Bull. Am. Meteorol. Soc. 2007, 88, 527–540. [Google Scholar] [CrossRef] [Green Version]
- Bentamy, A.; Grodsky, S.A.; Katsaros, K.; Mestas-Nuñez, A.M.; Blanke, B.; Desbiolles, F. Improvement in air–sea flux estimates derived from satellite observations. Int. J. Remote Sens. 2013, 34, 5243–5261. [Google Scholar] [CrossRef] [Green Version]
- Tomita, H.; Hihara, T.; Kako, S.I.; Kubota, M.; Kutsuwada, K. An introduction to J-OFURO3, a third-generation Japanese ocean flux data set using remote-sensing observations. J. Oceanogr. 2019, 75, 171–194. [Google Scholar] [CrossRef] [Green Version]
- Roberts, B.J.; Clayson, C.A.; Robertson, F.R. SeaFlux Data Products; NASA Global Hydrology Resource Center DAAC: Huntsville, AL, USA, 2020. [Google Scholar]
- Olmedo, E.; González-Haro, C.; Hoareau, N.; Umbert, M.; González-Gambau, V.; Martínez, J.; Gabarró, C.; Turiel, A. Nine years of SMOS sea surface salinity global maps at the Barcelona Expert Center. Earth Syst. Sci. Data 2021, 13, 857–888. [Google Scholar] [CrossRef]
- Boutin, J.; Vergely, J.-L.; Khvorostyanov, D. SMOS SSS L3 Maps Generated by CATDS CEC LOCEAN. Debias V7.0. SEANOE; SEANOE: Plouzané, France, 2022. [Google Scholar] [CrossRef]
- Boutin, J.; Reul, N.; Catany, R.; Koehler, J.; Martin, A.; Rouffi, F.; Arias, M.; Chakroun, M.; Corato, G.; Estella-Perez, V.; et al. ESA Sea Surface Salinity Climate Change Initiative (Sea_Surface_Salinity_cci): Weekly and Monthly Sea Surface Salinity Prod-ucts, v2. 31, for 2010 to 2019. 07 September 2020 ed.; NERC EDS Centre for Environmental Data Analysis: Gwynedd, UK, 2020. [Google Scholar] [CrossRef]
- Melnichenko, O. Multi-Mission Optimally Interpolated Sea Surface Salinity 7-Day Global Dataset V1; NASA Physical Oceanography DAAC: PO.DAAC: Pasadena, CA, USA, 2021. [Google Scholar] [CrossRef]
- Droghei, R.; Nardelli, B.B.; Santoleri, R. Combining in situ and satellite observations to retrieve salinity and density at the ocean surface. J. Atmos. Ocean. Technol. 2016, 33, 1211–1223. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef] [Green Version]
- Olson, W.S.; Masunaga, H. GMP.Combined Radar-Radiometer Algorithm Team. In GPM Combined Radar-Radiometer Precipitation Algorithm Theoretical Basis Document (Version 4); NASA: Washington, DC, USA, 2016. [Google Scholar]
- Knapp, K.R. Scientific data stewardship of International Satellite Cloud Climatology Project B1 global geostationary observations. J. Appl. Remote Sens. 2008, 2, 023548. [Google Scholar] [CrossRef]
- Adler, R.F.; Sapiano, M.R.; Huffman, G.J.; Wang, J.-J.; Gu, G.; Bolvin, D.; Chiu, L.; Schneider, U.; Becker, A.; Nelkin, E. The Global Precipitation Climatology Project (GPCP) monthly analysis (new version 2.3) and a review of 2017 global precipitation. Atmosphere 2018, 9, 138. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef] [Green Version]
- Schneider, U.; Finger, P.; Meyer-Christoffer, A.; Rustemeier, E.; Ziese, M.; Becker, A. Evaluating the Hydrological Cycle over Land Using the Newly-Corrected Precipitation Climatology from the Global Precipitation Climatology Centre (GPCC). Atmosphere 2017, 8, 52. [Google Scholar] [CrossRef] [Green Version]
- Knapp, K.R.; Ansari, S.; Bain, C.L.; Bourassa, M.A.; Dickinson, M.J.; Funk, C.; Helms, C.N.; Hennon, C.C.; Holmes, C.D.; Huffman, G.J.; et al. Globally Gridded Satellite Observations for Climate Studies. Bull. Am. Meteorol. Soc. 2011, 92, 893–907. [Google Scholar] [CrossRef]
- Ushio, T.; Sasashige, K.; Kubota, T.; Shige, S.; Okamoto, K.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M.; et al. A Kalman Filter Approach to the Global Satellite Mapping of Precipitation (GSMaP) from Combined Passive Microwave and Infrared Radiometric Data. J. Meteorol. Soc. Japan. Ser. II 2009, 87A, 137–151. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Japan. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef] [Green Version]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Singh, R.; Joshi, P.; Kishtawal, C. A new technique for estimation of surface latent heat fluxes using satellite-based observations. Mon. Weather Rev. 2005, 133, 2692–2710. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP–DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily High-Resolution-Blended Analyses for Sea Surface Temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk Parameterization of Air–Sea Fluxes: Updates and Verification for the COARE Algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Kummerow, D.C.; Berg, W.K.; Sapiano, M.R.; Program, N.C. NOAA Climate Data Record (CDR) of SSM/I and SSMIS Microwave Brightness Temperatures, CSU Version 1; National Centers for Environmental Information, NESDIS, NOAA: Greenbelt, MD, USA, 2013. [Google Scholar] [CrossRef]
- Freeman, E.; Woodruff, S.D.; Worley, S.J.; Lubker, S.J.; Kent, E.C.; Angel, W.E.; Berry, D.I.; Brohan, P.; Eastman, R.; Gates, L.; et al. ICOADS Release 3.0: A major update to the historical marine climate record. Int. J. Climatol. 2017, 37, 2211–2232. [Google Scholar] [CrossRef] [Green Version]
- Berrisford, P.; Dee, D.P.; Poli, P.; Brugge, R.; Fielding, M.; Fuentes, M.; Kållberg, P.W.; Kobayashi, S.; Uppala, S.; Simmons, A. The ERA-Interim archive Version 2.0; ECMWF: Shinfield, UK, 2011; Volume 23. [Google Scholar]
- Bentamy, A.; Grodsky, S.A.; Elyouncha, A.; Chapron, B.; Desbiolles, F. Homogenization of scatterometer wind retrievals. Int. J. Climatol. 2017, 37, 870–889. [Google Scholar] [CrossRef] [Green Version]
- Tomita, H.; Hihara, T.; Kubota, M. Improved Satellite Estimation of Near-Surface Humidity Using Vertical Water Vapor Profile Information. Geophys. Res. Lett. 2018, 45, 899–906. [Google Scholar] [CrossRef]
- Wentz, F.J.; Ricciardulli, L.; Gentemann, C.; Meissner, T.; Hilburn, K.A.; Scott, J. Remote Sensing Systems Coriolis WindSat, Environmental Suite on 0.25 deg grid, Version 7.0.1.; Remote Sensing Systems: Santa Rosa, CA, USA, 2013. [Google Scholar]
- Wentz, F.J. A 17-yr climate record of environmental parameters derived from the Tropical Rainfall Measuring Mission (TRMM) Microwave Imager. J. Clim. 2015, 28, 6882–6902. [Google Scholar] [CrossRef]
- Gaiser, P.W.; St Germain, K.M.; Twarog, E.M.; Poe, G.A.; Purdy, W.; Richardson, D.; Grossman, W.; Jones, W.L.; Spencer, D.; Golba, G. The WindSat spaceborne polarimetric microwave radiometer: Sensor description and early orbit performance. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2347–2361. [Google Scholar] [CrossRef]
- Piolle, J.-F.; Bentamy, A. Quickscat scatterometer-Mean wind fileds products-User Manual. Ifremer, Department of Oceanography from Space, Ref.: C2-MUT-W-03-IF, Version 1.0. 2002. Available online: http://apdrc.soest.hawaii.edu/doc/qscat_mwf.pdf (accessed on 20 April 2022).
- Berg, W.; Kroodsma, R.; Kummerow, C.D.; McKague, D.S. Fundamental Climate Data Records of Microwave Brightness Temperatures. Remote Sens. 2018, 10, 1306. [Google Scholar] [CrossRef] [Green Version]
- Roberts, J.B.; Clayson, C.A.; Robertson, F.R. Improving Near-Surface Retrievals of Surface Humidity Over the Global Open Oceans From Passive Microwave Observations. Earth Space Sci. 2019, 6, 1220–1233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roberts, J.B.; Clayson, C.A.; Robertson, F.R.; Jackson, D.L. Predicting near-surface atmospheric variables from Special Sensor Microwave/Imager using neural networks with a first-guess approach. J. Geophys. Res. Atmos. 2010, 115, D19113. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Edson, J.B.; Jampana, V.; Weller, R.A.; Bigorre, S.P.; Plueddemann, A.J.; Fairall, C.W.; Miller, S.D.; Mahrt, L.; Vickers, D.; Hersbach, H. On the Exchange of Momentum over the Open Ocean. J. Phys. Oceanogr. 2013, 43, 1589–1610. [Google Scholar] [CrossRef] [Green Version]
- Droppleman, J.D.; Mennella, R.A.; Evans, D.E. An airborne measurement of the salinity variations of the Mississippi River Outflow. J. Geophys. Res. 1970, 75, 5909–5913. [Google Scholar] [CrossRef]
- Lagerloef, G.; Colomb, F.R.; Le Vine, D.; Wentz, F.; Yueh, S.; Ruf, C.; Lilly, J.; Gunn, J.; Chao, Y.; Decharon, A. The Aquarius/SAC-D mission: Designed to meet the salinity remote-sensing challenge. Oceanography 2008, 21, 68–81. [Google Scholar] [CrossRef] [Green Version]
- Reul, N.; Fournier, S.; Boutin, J.; Hernandez, O.; Maes, C.; Chapron, B.; Alory, G.; Quilfen, Y.; Tenerelli, J.; Morisset, S.; et al. Sea surface salinity observations from space with the SMOS satellite: A new means to monitor the marine branch of the water cycle. Earth’s Hydrol. Cycle 2014, 35, 681–722. [Google Scholar] [CrossRef] [Green Version]
- Meissner, T.; Wentz, F.J. Remote Sensing Systems SMAP Ocean Surface Salinities [Level 2C, Level 3 Running 8-day, Level 3 Monthly], Version 2.0 Validated Release; Systems, R.S., Ed.; Santa Rosa, CA, USA, 2016. [Google Scholar] [CrossRef]
- Olmedo, E.; Martínez, J.; Turiel, A.; Ballabrera-Poy, J.; Portabella, M. Debiased non-Bayesian retrieval: A novel approach to SMOS Sea Surface Salinity. Remote Sens. Environ. 2017, 193, 103–126. [Google Scholar] [CrossRef]
- Zweng, M.M.; Reagan, J.R.; Antonov, J.I.; Locarnini, R.A.; Mishonov, A.V.; Boyer, T.P.; Garcia, H.E.; Baranova, O.K.; Johnson, D.R.; Seidov, D.; et al. World Ocean Atlas 2013, Volume 2: Salinity; Levitus, S., Mishonov, A., Eds.; Technical Ed: NOAA Atlas NESDIS 74; National Oceanographic Data Center: Silver Spring, MD, USA, 2013. [Google Scholar]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The operational sea surface temperature and sea ice analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Boutin, J.; Martin, N.; Kolodziejczyk, N.; Reverdin, G. Interannual anomalies of SMOS sea surface salinity. Remote Sens. Environ. 2016, 180, 128–136. [Google Scholar] [CrossRef]
- Boutin, J.; Vergely, J.-L.; Marchand, S.; d’Amico, F.; Hasson, A.; Kolodziejczyk, N.; Reul, N.; Reverdin, G.; Vialard, J. New SMOS Sea Surface Salinity with reduced systematic errors and improved variability. Remote Sens. Environ. 2018, 214, 115–134. [Google Scholar] [CrossRef] [Green Version]
- Kolodziejczyk, N.; Prigent-Mazella, A.; Gaillard, F. ISAS Temperature and Salinity Gridded Fields; SEANOE: Plouzané, France, 2021. [Google Scholar] [CrossRef]
- Kolodziejczyk, N.; Prigent-Mazella, A.; Gaillard, F. ISAS-SSS: In Situ Sea Surface Salinity Gridded Fields; SEANOE: Plouzané, France, 2018. [Google Scholar] [CrossRef]
- Boutin, J.; Reul, N.; Koehler, J.; Martin, A.; Catany, R.; Guimbard, S.; Rouffi, F.; Vergely, J.L.; Arias, M.; Chakroun, M.; et al. Satellite-Based Sea Surface Salinity Designed for Ocean and Climate Studies. J. Geophys. Res. Ocean. 2021, 126, e2021JC017676. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J. The 2004–2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program. Prog. Oceanogr. 2009, 82, 81–100. [Google Scholar] [CrossRef]
- Good, S.A.; Martin, M.J.; Rayner, N.A. EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J. Geophys. Res. Ocean. 2013, 118, 6704–6716. [Google Scholar] [CrossRef]
- Nardelli, B.B. A Novel Approach for the High-Resolution Interpolation of In Situ Sea Surface Salinity. J. Atmos. Ocean. Technol. 2012, 29, 867–879. [Google Scholar] [CrossRef]
- CATDS. CATDS-PDC L3OS 2Q—Debiased Daily Valid Ocean Salinity Values Product from SMOS Satellite; CATDS, Ed.; CNES, IFREMER, LOCEAN, ACRI: Brest, France, 2022. [Google Scholar]
- Boutin, J.; Vergely, J.-L.; Khvorostyanov, D. SMOS SSS L3 Maps Generated by CATDS CEC LOCEAN. Debias V3. 0; SEANOE: Plouzané, France, 2018. [Google Scholar]
- de Boyer Montégut, C.; Madec, G.; Fischer, A.S.; Lazar, A.; Iudicone, D. Mixed layer depth over the global ocean: An examination of profile data and a profile-based climatology. J. Geophys. Res. Ocean. 2004, 109, C12003. [Google Scholar] [CrossRef]
- Henderson-Sellers, B. A new formula for latent heat of vaporization of water as a function of temperature. Q. J. R. Meteorol. Soc. 1984, 110, 1186–1190. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Rogers, D.P.; Edson, J.B.; Young, G.S. Bulk parameterization of air-sea fluxes for Tropical Ocean-Global Atmosphere Coupled-Ocean Atmosphere Response Experiment. J. Geophys. Res. Ocean. 1996, 101, 3747–3764. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z. Intercomparison of Global Sea Surface Salinity from Multiple Datasets over 2011–2018. Remote Sens. 2021, 13, 811. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- McDougall, T.J.; Barker, P.M. Getting started with TEOS-10 and the Gibbs Seawater (GSW), Oceanographic Toolbox. SCOR/IAPSO WG 2011, 127, 1–28. [Google Scholar]
- Gutenstein, M.; Fennig, K.; Schröder, M.; Trent, T.; Bakan, S.; Roberts, J.B.; Robertson, F.R. Intercomparison of freshwater fluxes over ocean and investigations into water budget closure. Hydrol. Earth Syst. Sci. 2021, 25, 121–146. [Google Scholar] [CrossRef]
- Rao, R.R.; Sivakumar, R. On the possible mechanisms of the evolution of a mini-warm pool during the pre-summer monsoon season and the genesis of onset vortex in the South-Eastern Arabian Sea. Q. J. R. Meteorol. Soc. 1999, 125, 787–809. [Google Scholar] [CrossRef]
- Houndegnonto, O.J.; Kolodziejczyk, N.; Maes, C.; Bourlès, B.; Da-Allada, C.Y.; Reul, N. Seasonal Variability of Freshwater Plumes in the Eastern Gulf of Guinea as Inferred From Satellite Measurements. J. Geophys. Res. Ocean. 2021, 126, e2020JC017041. [Google Scholar] [CrossRef]
- Da-Allada, C.; Alory, G.; Penhoat, Y.d.; Kestenare, E.; Durand, F.; Hounkonnou, N. Seasonal mixed-layer salinity balance in the tropical Atlantic Ocean: Mean state and seasonal cycle. J. Geophys. Res. Ocean. 2013, 118, 332–345. [Google Scholar] [CrossRef] [Green Version]
- Aubone, N.; Palma, E.D.; Piola, A.R. The surface salinity maximum of the South Atlantic. Prog. Oceanogr. 2021, 191, 102499. [Google Scholar] [CrossRef]
- Schanze, J.J.; Schmitt, R.W.; Yu, L. The global oceanic freshwater cycle: A state-of-the-art quantification. J. Mar. Res. 2010, 68, 569–595. [Google Scholar] [CrossRef]
- Bentamy, A.; Katsaros, K.B.; Mestas-Nuñez, A.M.; Drennan, W.M.; Forde, E.B.; Roquet, H. Satellite Estimates of Wind Speed and Latent Heat Flux over the Global Oceans. J. Clim. 2003, 16, 637–656. [Google Scholar] [CrossRef] [Green Version]
- Font, J.; Lagerloef, G.S.E.; Vine, D.M.L.; Camps, A.; Zanife, O. The determination of surface salinity with the European SMOS space mission. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2196–2205. [Google Scholar] [CrossRef] [Green Version]
- Nieves, V.; Wang, J.; Willis, J.K. A conceptual model of ocean freshwater flux derived from sea surface salinity. Geophys. Res. Lett. 2014, 41, 6452–6458. [Google Scholar] [CrossRef]











| Number | Datasets | Version | Variables | Resolution | Temporal Coverage | Reference |
|---|---|---|---|---|---|---|
| 1 | GPCP | Version 3.1 | 0.5°, monthly | January 1983–December 2019 | Huffman et al. [23] | |
| 2 | CMAP | Version2112blended | 2.5°, monthly | January 1979 to present | Xie et al. [27] | |
| 3 | CMORPH | Version 1 | 0.25°, daily | January 1998–December 2021 | Xie et al. [28] | |
| 4 | GPM IMERG | Version 6 | 0.1°, monthly | Jun 2000–September 2021 | Huffman et al. [29] | |
| 5 | PERSIANN CDR | None | 0.25°, monthly | January 1983 to present | Ashouri et al. [30] | |
| 6 | TRMM 3B42 | Version 7 | 0.25°, daily | January 1983–December 2019 | Huffman et al. [31] | |
| 7 | MSWEP | Version 2.8 | 0.1°, monthly | February 1979–November 2020 | Beck et al. [32], Beck et al. [33] | |
| 8 | OAFlux | Version 3 | 1°, monthly | January 1958–December 2020 | Yu and Weller [34] | |
| 9 | IFREMER | Version 4.1 | , | 0.25°, monthly | January 1992–December 2018 | Bentamy et al. [35] |
| 10 | J-OFURO3 | Version 1.1 | , | 0.25°, monthly | January 1988–December 2017 | Tomita et al. [36] |
| 11 | SEAFLUX | Version 3 | , | 0.25°, monthly | January 1988–December 2018 | Roberts et al. [37] |
| 12 | SMOS BEC | BEC, Level 4 Version 2 | 0.05°, daily | January 2011–December 2019 | Olmedo et al. [38] | |
| 13 | SMOS CEC | Version 7, Level 3 | 0.25°, 4 days | January 2010–November 2021 | Boutin et al. [39] | |
| 14 | ESA CCI | Version 03.21 | longitude 0.26°, latitude 0.2~1.5°, monthly | January 2010–September 2020 | Boutin et al. [40] | |
| 15 | OISSS | Version 1.0 | 0.25°, 4 days | August 2011–November 2021 | Melnichenko [41] | |
| 16 | CMEMS | MULTIOBS-GLO-PHY-S-SURFACE-MYNRT-015-013 | 0.25°, monthly | January 1993–December 2020 | Droghei et al. [42] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Wei, Z.; Nie, X. Assessing the Relationship between Freshwater Flux and Sea Surface Salinity. Remote Sens. 2022, 14, 2149. https://doi.org/10.3390/rs14092149
Liu H, Wei Z, Nie X. Assessing the Relationship between Freshwater Flux and Sea Surface Salinity. Remote Sensing. 2022; 14(9):2149. https://doi.org/10.3390/rs14092149
Chicago/Turabian StyleLiu, Hao, Zexun Wei, and Xunwei Nie. 2022. "Assessing the Relationship between Freshwater Flux and Sea Surface Salinity" Remote Sensing 14, no. 9: 2149. https://doi.org/10.3390/rs14092149
APA StyleLiu, H., Wei, Z., & Nie, X. (2022). Assessing the Relationship between Freshwater Flux and Sea Surface Salinity. Remote Sensing, 14(9), 2149. https://doi.org/10.3390/rs14092149