Improved Generalized IHS Based on Total Variation for Pansharpening
Abstract
:1. Introduction
2. Related Works
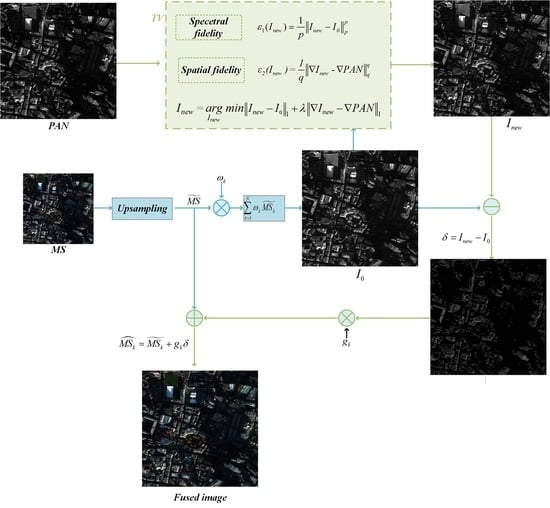
3. GIHS-TV Fusion Framework
3.1. Generalized IHS Transform
3.2. L1-TV Optimization
| Algorithm 1 The solution flow of in the GIHS-TV algorithm. |
|
4. Experiments
4.1. Datasets and Evaluation Metrics
4.2. Initial Results
4.3. Fusion Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Edwards, K.; Davis, P.A. The use of intensity-hue-saturation transformation for producing color shaded-relief images. Photogramm. Eng. Remote Sens. 1994, 60, 1369–1374. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2300–2312. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens. 2007, 46, 228–236. [Google Scholar] [CrossRef]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Restaino, R.; Scarpa, G.; Ulfarsson, M.O.; Alparone, L.; Chanussot, J. A new benchmark based on recent advances in multispectral pansharpening: Revisiting pansharpening with classical and emerging pansharpening methods. IEEE Geosci. Remote Sens. Mag. 2020, 9, 53–81. [Google Scholar] [CrossRef]
- Tu, T.M.; Su, S.C.; Shyu, H.C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- Javan, F.D.; Samadzadegan, F.; Mehravar, S.; Toosi, A.; Khatami, R.; Stein, A. A review of image fusion techniques for pan-sharpening of high-resolution satellite imagery. ISPRS J. Photogramm. Remote Sens. 2021, 171, 101–117. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Dalla Mura, M.; Licciardi, G.; Chanussot, J. Contrast and error-based fusion schemes for multispectral image pansharpening. IEEE Geosci. Remote Sens. Lett. 2013, 11, 930–934. [Google Scholar] [CrossRef] [Green Version]
- Ranchin, T.; Wald, L. Fusion of high spatial and spectral resolution images: The ARSIS concept and its implementation. Photogramm. Eng. Remote Sens. 2000, 66, 49–61. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2565–2586. [Google Scholar] [CrossRef]
- Otazu, X.; González-Audícana, M.; Fors, O.; Núñez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Xiao, L.; Tang, S.; Sun, L. Fractional order variational pan-sharpening. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2602–2605. [Google Scholar]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Pacifici, F. A benchmarking protocol for pansharpening: Dataset, preprocessing, and quality assessment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6102–6118. [Google Scholar] [CrossRef]
- Li, S.; Yang, B. A new pan-sharpening method using a compressed sensing technique. IEEE Trans. Geosci. Remote Sens. 2010, 49, 738–746. [Google Scholar] [CrossRef]
- Li, S.; Yin, H.; Fang, L. Remote sensing image fusion via sparse representations over learned dictionaries. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4779–4789. [Google Scholar] [CrossRef]
- Zhong, J.; Yang, B.; Huang, G.; Zhong, F.; Chen, Z. Remote sensing image fusion with convolutional neural network. Sens. Imaging 2016, 17, 10. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, C. A CNN-based pan-sharpening method for integrating panchromatic and multispectral images using Landsat 8. Remote Sens. 2019, 11, 2606. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Z.; Wang, D.; Tan, W.; Yu, G.; You, J.; Lv, B.; Wu, Z. RCSANet: A Full Convolutional Network for Extracting Inland Aquaculture Ponds from High-Spatial-Resolution Images. Remote Sens. 2020, 13, 92. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, Z.; Liu, H.; Xie, G. MSDRN: Pansharpening of multispectral images via multi-scale deep residual network. Remote Sens. 2021, 13, 1200. [Google Scholar] [CrossRef]
- Liu, Q.; Han, L.; Tan, R.; Fan, H.; Li, W.; Zhu, H.; Du, B.; Liu, S. Hybrid attention based residual network for pansharpening. Remote Sens. 2021, 13, 1962. [Google Scholar] [CrossRef]
- Wu, Y.; Feng, S.; Lin, C.; Zhou, H.; Huang, M. A three stages detail injection network for remote sensing images pansharpening. Remote Sens. 2022, 14, 1077. [Google Scholar] [CrossRef]
- Yin, J.; Qu, J.; Sun, L.; Huang, W.; Chen, Q. A Local and Nonlocal Feature Interaction Network for Pansharpening. Remote Sens. 2022, 14, 3743. [Google Scholar] [CrossRef]
- Nie, Z.; Chen, L.; Jeon, S.; Yang, X. Spectral-Spatial Interaction Network for Multispectral Image and Panchromatic Image Fusion. Remote Sens. 2022, 14, 4100. [Google Scholar] [CrossRef]
- Jian, L.; Wu, S.; Chen, L.; Vivone, G.; Rayhana, R.; Zhang, D. Multi-Scale and Multi-Stream Fusion Network for Pansharpening. Remote Sens. 2023, 15, 1666. [Google Scholar] [CrossRef]
- Ciotola, M.; Scarpa, G. Fast Full-Resolution Target-Adaptive CNN-Based Pansharpening Framework. Remote Sens. 2023, 15, 319. [Google Scholar] [CrossRef]
- Ma, J.; Yu, W.; Chen, C.; Liang, P.; Guo, X.; Jiang, J. Pan-GAN: An unsupervised pan-sharpening method for remote sensing image fusion. Inf. Fusion 2020, 62, 110–120. [Google Scholar] [CrossRef]
- Zhang, L.; Li, W.; Huang, H.; Lei, D. A pansharpening generative adversarial network with multilevel structure enhancement and a multistream fusion architecture. Remote Sens. 2021, 13, 2423. [Google Scholar] [CrossRef]
- Gastineau, A.; Aujol, J.F.; Berthoumieu, Y.; Germain, C. Generative adversarial network for pansharpening with spectral and spatial discriminators. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4401611. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, H.; Xu, Q.; Liu, X.; Wang, Y. PSGAN: A generative adversarial network for remote sensing image pan-sharpening. IEEE Trans. Geosci. Remote Sens. 2020, 59, 10227–10242. [Google Scholar] [CrossRef]
- Jozdani, S.; Chen, D.; Chen, W.; Leblanc, S.G.; Lovitt, J.; He, L.; Fraser, R.H.; Johnson, B.A. Evaluating Image Normalization via GANs for Environmental Mapping: A Case Study of Lichen Mapping Using High-Resolution Satellite Imagery. Remote Sens. 2021, 13, 5035. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Yu, K.; Kim, Y. A new adaptive component-substitution-based satellite image fusion by using partial replacement. IEEE Trans. Geosci. Remote Sens. 2010, 49, 295–309. [Google Scholar] [CrossRef]
- Carper, W.; Lillesand, T.; Kiefer, R. The use of intensity-hue-saturation transformations for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens. 1990, 56, 459–467. [Google Scholar]
- Kwarteng, P.; Chavez, A. Extracting spectral contrast in Landsat Thematic Mapper image data using selective principal component analysis. Photogramm. Eng. Remote Sens. 1989, 55, 339–348. [Google Scholar]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. II. Channel ratio and “chromaticity” transformation techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Vivone, G. Robust band-dependent spatial-detail approaches for panchromatic sharpening. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6421–6433. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. An MTF-based spectral distortion minimizing model for pan-sharpening of very high resolution multispectral images of urban areas. In Proceedings of the 2003 2nd GRSS/ISPRS Joint Workshop on Remote Sensing and Data Fusion over Urban Areas, Berlin, Germany, 22–23 May 2003; pp. 90–94. [Google Scholar]
- Chavez, P.; Sides, S.C.; Anderson, J.A. Comparison of three different methods to merge multiresolution and multispectral data- Landsat TM and SPOT panchromatic. Photogramm. Eng. Remote Sens. 1991, 57, 295–303. [Google Scholar]
- Khan, M.M.; Chanussot, J.; Condat, L.; Montanvert, A. Indusion: Fusion of multispectral and panchromatic images using the induction scaling technique. IEEE Geosci. Remote Sens. Lett. 2008, 5, 98–102. [Google Scholar] [CrossRef] [Green Version]
- Liu, J. Smoothing filter-based intensity modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T. Liu’Smoothing filter-based intensity modulation: A spectral preserve image fusion technique for improving spatial details’. Int. J. Remote Sens. 2002, 23, 593–597. [Google Scholar] [CrossRef]
- Dong, W.; Xiao, S.; Li, Y.; Qu, J. Hyperspectral pansharpening based on intrinsic image decomposition and weighted least squares filter. Remote Sens. 2018, 10, 445. [Google Scholar] [CrossRef] [Green Version]
- Ballester, C.; Caselles, V.; Igual, L.; Verdera, J.; Rougé, B. A variational model for P+ XS image fusion. Int. J. Comput. Vis. 2006, 69, 43. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A new pansharpening algorithm based on total variation. IEEE Geosci. Remote Sens. Lett. 2013, 11, 318–322. [Google Scholar] [CrossRef]
- He, X.; Condat, L.; Bioucas-Dias, J.M.; Chanussot, J.; Xia, J. A new pansharpening method based on spatial and spectral sparsity priors. IEEE Trans. Image Process. 2014, 23, 4160–4174. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Chen, Y.; Yang, C.; Gao, X.; Ma, J. A variational pansharpening method based on gradient sparse representation. IEEE Signal Process. Lett. 2020, 27, 1180–1184. [Google Scholar] [CrossRef]
- Fasbender, D.; Radoux, J.; Bogaert, P. Bayesian data fusion for adaptable image pansharpening. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1847–1857. [Google Scholar] [CrossRef]
- Möller, M.; Wittman, T.; Bertozzi, A.L.; Burger, M. A variational approach for sharpening high dimensional images. SIAM J. Imaging Sci. 2012, 5, 150–178. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Fang, F.; Zhou, A.; Li, F. Pan-sharpening of multi-spectral images using a new variational model. Int. J. Remote Sens. 2015, 36, 1484–1508. [Google Scholar] [CrossRef]
- Duran, J.; Buades, A.; Coll, B.; Sbert, C. A nonlocal variational model for pansharpening image fusion. SIAM J. Imaging Sci. 2014, 7, 761–796. [Google Scholar] [CrossRef]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5449–5457. [Google Scholar]
- Xu, S.; Zhang, J.; Zhao, Z.; Sun, K.; Liu, J.; Zhang, C. Deep gradient projection networks for pan-sharpening. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1366–1375. [Google Scholar]
- Zhang, X.; Dai, X.; Zhang, X.; Jin, G. Joint principal component analysis and total variation for infrared and visible image fusion. Infrared Phys. Technol. 2023, 128, 104523. [Google Scholar] [CrossRef]
- Rodríguez, P.; Wohlberg, B. Efficient minimization method for a generalized total variation functional. IEEE Trans. Image Process. 2008, 18, 322–332. [Google Scholar] [CrossRef] [PubMed]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In JPL, Summaries of the Third Annual JPL Airborne Geoscience Workshop, Volume 1: AVIRIS Workshop; NASA: Washington, DC, USA, 1992. [Google Scholar]
- Zhou, J.; Civco, D.L.; Silander, J.A. A wavelet transform method to merge Landsat TM and SPOT panchromatic data. Int. J. Remote Sens. 1998, 19, 743–757. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef] [Green Version]













| Method | QNR | SAM | SCC | ||
|---|---|---|---|---|---|
| HPF | 0.0651 | 0.1031 | 0.8389 | 1.5775 | 0.8600 |
| SFIM | 0.0644 | 0.0998 | 0.8427 | 1.2277 | 0.8559 |
| Indusion | 0.0613 | 0.0882 | 0.8562 | 2.7859 | 0.8040 |
| ATWT | 0.0769 | 0.1115 | 0.8206 | 1.8998 | 0.8738 |
| AWLP | 0.0637 | 0.0964 | 0.8463 | 2.0627 | 0.8302 |
| ATWT-M2 | 0.0581 | 0.1375 | 0.8132 | 2.0203 | 0.8408 |
| ATWT-M3 | 0.0666 | 0.1221 | 0.8203 | 1.9297 | 0.8606 |
| MTF-GLP | 0.0794 | 0.1149 | 0.8152 | 2.0113 | 0.8789 |
| MTF-GLP-HPM-PP | 0.1065 | 0.1354 | 0.7730 | 2.4969 | 0.8948 |
| MTF-GLP-HPM | 0.0788 | 0.1097 | 0.8206 | 1.4539 | 0.8707 |
| MTF-GLP-CBD | 0.0773 | 0.1135 | 0.8184 | 2.1497 | 0.8742 |
| GIHS-TV () | 0.0550 | 0.0876 | 0.8624 | 0.6090 | 0.8760 |
| Methods | GE_Tren_Urb | W3_Muni_Urb | W3_Muni_Mix | W4_Mexi_Nat |
|---|---|---|---|---|
| P+XS | 197.7686 | 397.8795 | 420.6308 | 207.6450 |
| GIHS-TV | 27.6508 | 23.0162 | 26.5074 | 24.2559 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Dai, X.; Zhang, X.; Hu, Y.; Kang, Y.; Jin, G. Improved Generalized IHS Based on Total Variation for Pansharpening. Remote Sens. 2023, 15, 2945. https://doi.org/10.3390/rs15112945
Zhang X, Dai X, Zhang X, Hu Y, Kang Y, Jin G. Improved Generalized IHS Based on Total Variation for Pansharpening. Remote Sensing. 2023; 15(11):2945. https://doi.org/10.3390/rs15112945
Chicago/Turabian StyleZhang, Xuefeng, Xiaobing Dai, Xuemin Zhang, Yuchen Hu, Yingdong Kang, and Guang Jin. 2023. "Improved Generalized IHS Based on Total Variation for Pansharpening" Remote Sensing 15, no. 11: 2945. https://doi.org/10.3390/rs15112945
APA StyleZhang, X., Dai, X., Zhang, X., Hu, Y., Kang, Y., & Jin, G. (2023). Improved Generalized IHS Based on Total Variation for Pansharpening. Remote Sensing, 15(11), 2945. https://doi.org/10.3390/rs15112945