Water Surface Acoustic Wave Detection by a Millimeter Wave Radar
Abstract
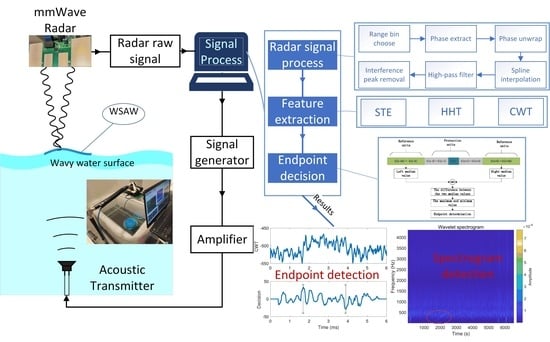
:1. Introduction
2. Principle and System
2.1. WSAW Properties
2.2. System
2.3. mmWave Radar Detection Principle
2.4. Radar Signal Preprocessing
3. Algorithms for WSAW Endpoint Detection
3.1. Feature Extraction
3.1.1. Short-Time Energy Algorithm
3.1.2. Hilbert Huang Transform (HHT) Algorithm
3.1.3. Continuous Wavelet Transform (CWT) Algorithm
3.2. Decision Method
- (1)
- Setting the lengths of reference and protection units.The length is set according to the length of the WSAW and the power ratio of WSAW phase signal to the noise phase signal (SNR). Without losing generality, we set the length of reference units as 40, and the length of the protection unit is 4.
- (2)
- For the edge value (the first and last 40 points), the lengths of the reference unit are less than the setting value.
- (3)
- Calculating the left and right median values within the reference units.
- (4)
- Calculating the difference between the left and right median values.
- (5)
- Setting edge protection by setting the first and last 50 difference points values as 0.
- (6)
- Finding the maximum and minimum values of the median difference between the two sides.
- (7)
- Making the maximum and minimum difference as the endpoint.
4. Simulation Test
4.1. Wavy Ocean Surface Simulation
4.2. Algorithms Simulation
5. Experiment and Discussion
5.1. Experiment Describtion
5.2. Experiment Results on Still Water Surface
5.3. Experiment Results on Wavy Water Surface
5.4. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L. Research on Optical Heterodyne Detection Technology for Acoustically Induced Water Surface Capillary Waves. Ph.D. Thesis, Harbin Industrial University, Harbin, China, 2017. [Google Scholar]
- Whitcomb, L.; Yoerger, D.R.; Singh, H.; Howland, J. Advances in Underwater Robot Vehicles for Deep Ocean Exploration: Navigation, Control, and Survey Operations. In Robotics Research; Springer: Berlin/Heidelberg, Germany, 2000; pp. 439–448. [Google Scholar]
- Adler, R.; Korpel, A.; Desmares, P. An instrument for making surface waves visible. IEEE Trans. Sonics Ultrason. 1968, 15, 157–160. [Google Scholar] [CrossRef]
- Berg, N.J.; Lee, J.N. Acousto-Optic Signal Processing: Theory and Implementation; M. Dekker: New York, NY, USA, 1983. [Google Scholar]
- Churnside, J.H.; Bravo, H.E.; Naugolnykh, K.A.; Fuks, I.M. Effects of underwater sound and surface ripples on scattered laser light. Acoust. Phys. 2008, 54, 204–209. [Google Scholar] [CrossRef]
- Antonelli, L.; Blackmon, F. Experimental demonstration of remote, passive acousto-optic sensing. J. Acoust. Soc. Am. 2004, 116, 3393. [Google Scholar] [CrossRef] [PubMed]
- Weisbuch, G. Light scattering by surface tension waves. Am. J. Phys. 1979, 47, 355. [Google Scholar] [CrossRef]
- Barik, T.K.; Chaudhuri, P.R.; Roy, A.; Kar, S. Probing liquid surface waves, liquid properties and liquid films with light diffraction. Meas. Sci. Technol. 2006, 17, 1553. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.S.; Bourgeois, B.S.; Hsieh, S.T.; Martinez, A.B.; Hickman, G.D. A laser sensing scheme for detection of underwater acoustic signals. In Proceedings of the Southeastcon 88, IEEE Conference, Knoxville, TN, USA, 10–13 April 1988. [Google Scholar]
- Matthews, A.D.; Arrieta, L.L. Acoustic optic hybrid (AOH) sensor. J. Acoust. Soc. Am. 2000, 108, 1089–1093. [Google Scholar] [CrossRef]
- Blackmon, F.A.; Antonelli, L.T. Experimental Detection and Reception Performance for Uplink Underwater Acoustic Communication. IEEE J. Ocean. Eng. 2006, 31, 179–187. [Google Scholar] [CrossRef]
- Farrant, D.; Burke, J.; Dickinson, L.; Fairman, P.; Wendoloski, J. Opto-acoustic underwater remote sensing (OAURS) an optical sonar? In Proceedings of the OCEANS’10, Sydney, NSW, Australia, 24–27 May 2010. [Google Scholar]
- Tremain, D.; Angelakos, D. Detection of underwater sound sources by microwave radiation reflected from the water surface. Proc. IEEE 1972, 60, 741–742. [Google Scholar] [CrossRef]
- Tonolini, F.; Adib, F. Networking across boundaries: Enabling wireless communication through the water–air interface. In Proceedings of the 2018 Conference of the ACM Special Interest Group, Budapest, Hungary, 20–25 August 2018. [Google Scholar]
- Qu, F.; Qian, J.; Wang, J.; Lu, X.; Zhang, M.; Bai, X.; Ran, Z.; Tu, X.; Liu, Z.; Wei, Y. Cross-Medium Communication Combining Acoustic Wave and Millimeter Wave: Theoretical Channel Model and Experiments. IEEE J. Ocean. Eng. 2022, 47, 483–492. [Google Scholar] [CrossRef]
- Guo, C.; Deng, B.; Yang, Q.; Wang, H.; Liu, K. Modeling and Simulation of Water-surface Vibration due to Acoustic Signals for Detection with Terahertz Radar. In Proceedings of the UK-Europe-China Workshop on Millimeter Waves and Terahertz Technologies, London, UK, 20–22 August 2019. [Google Scholar]
- Luo, J.; Liang, X.; Guo, Q.; Zhao, T.; Xin, J.; Bu, X. A Novel Estimation Method of Water Surface Micro-Amplitude Wave Frequency for Cross-Media Communication. Remote. Sens. 2022, 14, 5889. [Google Scholar] [CrossRef]
- Liu, B.; Lei, J. Principles of Underwater Acoustics; Harbin Engineering University Press: Harbin, China, 2009. [Google Scholar]
- Li, C.; Cummings, J.; Lam, J.; Graves, E.; Wu, W. Radar remote monitoring of vital signs. IEEE Microw. Mag. 2009, 10, 47–56. [Google Scholar] [CrossRef]
- Zhang, T.; Shao, Y.; Wu, Y.; Geng, Y.; Fan, L. An overview of speech endpoint detection algorithms. Appl. Acoust. 2020, 160, 107133. [Google Scholar] [CrossRef]
- Wilpon, J.G.; Rabiner, L.R.; Martin, T. An Improved Word-Detection Algorithm for Telephone-Quality Speech Incorporating Both Syntactic and Semantic Constraints. AT&T Bell Lab. Tech. J. 1984, 63, 479–498. [Google Scholar]
- Sun, M.; Wan, G.; Zhuang, X.; Zhou, J.; Shen, Y.; Zhang, M.; Du, H. Aerial remote sensing of underwater acoustic signal based on laser interference. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–4. [Google Scholar]
- Yan, R.; Gao, R.X. Hilbert-Huang Transform Based Vibration Signal Analysis for Machine Health Monitoring. IEEE Trans. Instrum. Meas. 2006, 55, 2320–2329. [Google Scholar] [CrossRef]
- Hai, H.; Pan, J. Speech pitch determination based on Hilbert-Huang transform. Signal Processing 2006, 86, 792–803. [Google Scholar]
- Zhang, R.R.; Asce, M.; Ma, S.; Safak, E.; Hartzell, S. Hilbert-Huang Transform Analysis of Dynamic and Earthquake Motion Recordings. J. Eng. Mech. 2003, 129, 861–875. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P. On empirical mode decomposition and its algorithms. In Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing, Grado, Italy, 8 June 2003; Volume 3, pp. 8–11. [Google Scholar]
- Wang, G.; Chen, X.Y.; Qiao, F.L.; Wu, Z.; Huang, N.E. On intrinsic mode function. Advances in Adaptive Data Analysis 2010, 2, 277–293. [Google Scholar] [CrossRef]
- Sinha, S.; Routh, P.S.; Anno, P.D.; Castagna, J.P. Spectral decomposition of seismic data with continuous-wavelet transform. Geophysics 2005, 70, P19–P25. [Google Scholar] [CrossRef]
- Olhede, S.C.; Walden, A.T. Generalized Morse wavelets. IEEE Trans. Signal Process. 2002, 50, 2661–2670. [Google Scholar] [CrossRef] [Green Version]
- Aguiar-Conraria, L.; Soares, M.J. The Continuous Wavelet Transform: A Primer; Technical Report; NIPE-Universidade do Minho: Braga, Portugal, 2011. [Google Scholar]
- Pierson, W.J., Jr.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, P.; Ye, H. Theory and Method of Numerical Simulation of Composite Scattering from the Object and Randomly Rough Surface; Science Press: Beijing, China, 2008. [Google Scholar]
- Nikias, C.L.; Shao, M. Signal Processing with Alpha-Stable Distributions and Applications; Wiley-Interscience: Hoboken, NJ, USA, 1995. [Google Scholar]
- Qiu, T.; Zhang, X.; Li, X. Statistical Signal Processing: Non-Gaussian Signal Processing and Its Applications; Publishing Housing of Electronics Industry: Beijing, China, 2004. [Google Scholar]
- Laguna-Sanchez, G.; Lopez-Guerrero, M. On the use of alpha-stable distributions in noise modeling for PLC. IEEE Trans. Power Deliv. 2015, 30, 1863–1870. [Google Scholar]
- AWR1243BOOST. 2020. Available online: https://www.ti.com.cn/tool/cn/AWR1243BOOST (accessed on 10 May 2021).
- Chen, S.Z.; Zhang, X.L.; Wang, B.; Zhao, W.J.; Zhang, K.K.; Zhao, Q.; Yu-Shang, W.U. Review on the Progress of Water Surface Acoustic Wave Inspection for the Laser-Acoustic Detection Technique. J. Ocean. Technol. 2016, 35, 1–12. [Google Scholar]
- Xiaolin, Z.; Hongjie, M.; Kai, L.; Wenyan, T. Amplitude detection of low frequency water surface acoustic wave based on phase demodulation. Infrared Laser Eng. 2019, 48, 506001. [Google Scholar]



















| Phase | 0.5 mrad | 1 mrad | 1.5 mrad | 2 mrad | 2.5 mrad | |
|---|---|---|---|---|---|---|
| Method | ||||||
| STE | 5.4% | 10.9% | 26.1% | 53.1 % | 80.1 % | |
| HHT | 5.3% | 12.9% | 35.4% | 67.5% | 89.1% | |
| CWT | 6.5% | 18.0% | 44.4% | 75.5% | 93.2% |
| Phase | 0.5 mrad | 1 mrad | 1.5 mrad | 2 mrad | 2.5 mrad |
|---|---|---|---|---|---|
| Amp | 155 nm | 310 nm | 465 nm | 620 nm | 775 nm |
| Method | STE | HHT | CWT | |
|---|---|---|---|---|
| Wind Speed | ||||
| 2 m/s | 25.1% | 84.9% | 91.8% | |
| 4 m/s | 4.5% | 73.6% | 82.8% | |
| 6 m/s | 0.1% | 53.3% | 53.2% |
| Parameters | Value |
|---|---|
| Frequency | 77 GHz |
| Bandwidth | 1.53 GHz |
| Sample rate | 10 M/s |
| Chirp period | 100 s |
| chirp number | 255 |
| Frame number | 256 |
| Range resolution | 9.8 cm |
| Beam width for | |
| Beam width for |
| Organization | Time | Wave Length | Apply | Amptitude | Height | Frequency |
|---|---|---|---|---|---|---|
| Naval Research Office | 1972 | 8 mm | Detection | 1.6/0.8 mm | 45/55 Hz | |
| MIT Media Lab | 2018 | 5 mm | Comunication | micrometer | 20–40 cm | 200 Hz |
| Zhejiang University | 2022 | 3.9 mm | Comunication | micrometer | 3–50 cm | <4.4 KHz |
| This work | 2022 | 3.9 mm | Detection | <155 nm | 80 cm | <500 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Shen, S.; Xu, Z. Water Surface Acoustic Wave Detection by a Millimeter Wave Radar. Remote Sens. 2023, 15, 4022. https://doi.org/10.3390/rs15164022
Zeng Y, Shen S, Xu Z. Water Surface Acoustic Wave Detection by a Millimeter Wave Radar. Remote Sensing. 2023; 15(16):4022. https://doi.org/10.3390/rs15164022
Chicago/Turabian StyleZeng, Yuming, Siyi Shen, and Zhiwei Xu. 2023. "Water Surface Acoustic Wave Detection by a Millimeter Wave Radar" Remote Sensing 15, no. 16: 4022. https://doi.org/10.3390/rs15164022
APA StyleZeng, Y., Shen, S., & Xu, Z. (2023). Water Surface Acoustic Wave Detection by a Millimeter Wave Radar. Remote Sensing, 15(16), 4022. https://doi.org/10.3390/rs15164022