Next Article in Journal
Use of High-Resolution Land Cover Maps to Support the Maintenance of the NWI Geospatial Dataset: A Case Study in a Coastal New Orleans Region
Next Article in Special Issue
Study on Road Network Vulnerability Considering the Risk of Landslide Geological Disasters in China’s Tibet
Previous Article in Journal
DOA Estimation of Multiple Coherent Targets Using Weight Vector Orthogonal Decomposition in TDM-MIMO HF-Radar
Previous Article in Special Issue
An Approach for Monitoring Shallow Surface Outcrop Mining Activities Based on Multisource Satellite Remote Sensing Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 16
10.3390/rs15164074
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Spatial Data-Driven Approach for Mineral Prospectivity Mapping

by
Indishe P. Senanayake
1,2,3,*,
Anthony S. Kiem
1,3,
Gregory R. Hancock
1,3,
Václav Metelka
3,4,†,
Chris B. Folkes
5,
Phillip L. Blevin
5 and
Anthony R. Budd
3,6
1
School of Environmental and Life Sciences, College of Engineering, Science and Environment, The University of Newcastle, Callaghan, NSW 2308, Australia
2
School of Engineering, College of Engineering, Science and Environment, The University of Newcastle, Callaghan, NSW 2308, Australia
3
Mineral Exploration Cooperative Research Centre, Kensington, WA 6151, Australia
4
The Commonwealth Scientific and Industrial Research Organisation, Kensington, WA 6151, Australia
5
Geological Survey of New South Wales, Department of Regional NSW, Maitland, NSW 2310, Australia
6
Geoscience Australia, Canberra, ACT 2609, Australia
*
Author to whom correspondence should be addressed.
†
Current affiliation: AIC Mines Ltd., Subiaco, WA 6008, Australia.
Remote Sens. 2023, 15(16), 4074; https://doi.org/10.3390/rs15164074
Submission received: 25 July 2023 / Revised: 14 August 2023 / Accepted: 15 August 2023 / Published: 18 August 2023
(This article belongs to the Special Issue Remote Sensing for Geology and Mapping)
Browse Figures
Versions Notes

Abstract

:
Mineral prospectivity mapping is a crucial technique for discovering new economic mineral deposits. However, detailed knowledge-based geological exploration and interpretations generally involve significant costs, time, and human resources. In this study, an ensemble machine learning approach was tested using geoscience datasets to map Cu-Au and Pb-Zn mineral prospectivity in the Cobar Basin, NSW, Australia. The input datasets (magnetic, gravity, faults, electromagnetic, and magnetotelluric data layers) were chosen by considering their association with Cu-Au and Pb-Zn mineralization patterns. Three machine learning algorithms, namely random forest (RF), support vector machine (SVM), and maximum-likelihood (MaxL) classification, were applied to the input data. The results of the three algorithms were ensembled to produce Cu-Au and Pb-Zn prospectivity maps over the Cobar Basin with improved classification accuracy. The findings demonstrate good agreement with known mineral occurrence points and existing mineral prospectivity maps developed using the weights-of-evidence (WofE) method. The ability to capture training points accurately and the simplicity of the proposed approach make it advantageous over complex mineral prospectivity mapping methods, to serve as a preliminary evaluation technique. The methodology can be modified with different datasets and algorithms, facilitating the investigations of mineral prospectivity in other regions and providing guidance for more detailed, high-resolution geological investigations.

Graphical Abstract

1. Introduction

Mineral prospectivity mapping aids the discovery of new ore deposits and plays a vital role in mineral exploration and the mining industry. Geological, geochemical, geophysical, and remotely sensed datasets are commonly employed in mineral prospectivity mapping approaches, by analysing them with various geo-computational techniques to identify key mineralisation patterns (e.g., Refs. [1,2,3,4]). Geophysical methods, such as seismic and electromagnetic (EM) surveys, help detect subsurface variations in the physical properties that may indicate mineralization [5,6]. Geochemical analyses of rock and soil samples unveil elemental compositions, helping in identifying anomaly patterns associated with mineral deposits [7,8]. Remote sensing methods, like satellite imagery and airborne surveys, enable the detection of surface alterations, mineral signatures, and topographic features, enhancing the identification of potential exploration targets [9,10,11]. The integration of these multidisciplinary datasets and methods offers a robust approach to mineral exploration, aiding in the delineation and assessment of prospective areas for further investigation [12].
Mineral prospectivity mapping techniques can be classified mainly into two categories: (i) expert-knowledge-driven (EKD, e.g., Refs. [13,14,15]); and (ii) data-driven (e.g., Refs. [16,17,18]) approaches. EKD approaches employ geological expertise who possess a deep understanding of the geological formations and mineral indicators to identify and interpret new deposits, whereas data-driven approaches employ the spatial associations of different geoscience datasets to map mineral potential. The EKD methods incorporate domain-specific insights, leading to targeted and informed exploration efforts. However, it might be limited by subjectivity and biases associated with human decision-making, potentially overlooking unconventional mineralization patterns or rare deposits. On the contrary, data-driven approaches employ advanced technologies such as remote sensing, machine learning, and geospatial analysis to process large datasets and identify spatial patterns and anomalies. While data-driven methods offer objectivity, speed, and the potential to find unrecognized mineral occurrences, they can be limited by data quality issues, algorithmic uncertainties, and the risk of false positives. Probabilistic methods, such as weights-of-evidence (WofE) and logistic regression, have been previously used for many mineral prospectivity mapping studies across the globe [19,20,21,22] and are now more widely accepted in the mining industry. Still, the prevalent method for generating new targets and evaluating the potential of mineralisation, especially in mid-tier and junior mineral houses, remains EKD in some aspects. However, these EKD methods require more specialised human resources, often implying higher costs, as well as longer project timeframes.
Classification can be identified as the main process used in data-driven mineral prospectivity mapping. The outputs of classification methods classify locations as prospective or non-prospective, as binary maps or maps showing a prospectivity confidence range. Classification approaches are primarily categorised into (i) supervised and (ii) unsupervised methods. In supervised methods, the model is trained with given training samples, whereas in unsupervised methods, clusters are generated based on the similarities and dissimilarities of the spatial data.
Often the association between mineralisation patterns and geospatial datasets is complex and non-linear. In this context, machine learning algorithms can be a viable option to capture these complex relationships between input data and mineralisation patterns. Many researchers have tested machine learning methods to map mineral prospectivity, which often outperform the traditional statistical and empirical explorative models [23,24,25,26,27,28]. Brown et al. [23] have used a multilayer feed-forward neural network, trained with a gradient descent back-propagation algorithm to map Au prospectivity in Tenterfield, NSW, Australia. The neural network performed well, even with one-third less data than a WofE method. Zuo and Carranza [29] tested a support vector machine (SVM) algorithm to map Au prospectivity in the western Meguma Terrain of Canada. Their results showed that the SVM method outperformed the WofE approach. McKay and Harris [25] tested random forest (RF) methods to map Au mineralisation in Hearn Geologic Province in Nunavut, Canada and observed a better performance than knowledge-driven methods. A RF-based data-driven method employed by Carranza and Laborte [16] outperformed the evidential belief modelling in mapping the hydrothermal Au-Cu prospectivity in Catanduanes Island, Philippines. However, the results of different classification methods can never be entirely identical due to the nature of the algorithms. Therefore, outputs from a single algorithm can inherit particular errors or biases.
This study aims to assess a simple data-driven machine learning approach to map mineral prospectivity, which can produce quick results on a large scale and can be used as an initial guide for more detailed geological evaluations. This data-driven approach has minimal involvement of geological expertise (i.e., it remains more objective with less potential for human-induced bias). Therefore, less human resources and time are required for this method. This study aims to investigate the performance of three machine learning algorithms, (i) RF, (ii) SVM, and (iii) maximum-likelihood classification (MaxL) in south-eastern Australia to map Cu-Au and Pb-Zn mineralisation patterns over the Cobar Basin, NSW, Australia with a unique combination of input geoscience datasets. Given the possible errors inherited in the outputs of a single classification algorithm, a simple ensemble method is employed in this study to combine the results of the three classification algorithms.

2. Study Area

The Cobar Superbasin in the Central Lachlan Orogen (Figure 1) is a mineral-rich Late Silurian to Early Devonian basin found in central-western NSW, about 700 km northwest of Sydney. The basin is NSW’s most heavily mineralised Siluro-Devonian basin, enriched with precious and base metal mineral systems [30,31]. An overview of the geology of the Cobar Basin is described by Folkes et al. [32], and a detailed description of its structural framework is given by Glen et al. [33]. The Cobar area has a long history of mining and exploration dating back to 1869, when copper was discovered in the area. The Cobar Basin is a major polymetallic mineral province, including Au-only, Au- and Ag-rich, and Cu-and Pb-Zn-rich systems, with a total estimated metal endowment (past production plus known resources) exceeding 224.54 t Au, 2.519 Mt Cu, 2.801 Mt Pb, 4.760 Mt Zn, and 6924 t Ag [34,35].
Fitzherbert and Downes [35] and Ford et al. [31] provide good overviews of the tectonic and mineralisation history of the basin. The following is taken from these sources (and references therein). Geologically, the Cobar Basin rocks underwent three main tectonic phases,
  • Rift phase deposition and widespread volcanism in discrete volcanic troughs/belts ca. 420 Ma;
  • Transition to sag phase deposition at ca. 410 Ma, with stable sag phase deposition continuing until ca. 400 Ma. Bindian extension/contraction at ca. 410 Ma; and
  • Inversion phase during the Tabberabberan Orogeny ca. 390–380 Ma.
Fault-focused mineralisation is associated with these three tectonic phases, often resulting in the formation of complex polymetallic orebodies. The mineralisation mainly occurred after the transition to the sag phase basin deposition, whereas only a few orebodies have been formed at the rift phase volcanism/basin deposition.
Three major mineralisation systems can be found in and around the Cobar Basin: (i) Cu-Au-±Zn mineralisation; (ii) Pb-Zn mineralisation; and (iii) Sn-W mineralisation. The Cobar Cu-Au mineralisation extends mainly along the eastern boundary of the basin, with fewer occurrences in the western and southern parts of the basin. The style of these deposits varies from the massive sulphide-rich zones to the breccia, vein, or shear-hosted mineralisation. Some zones form multiple narrow ore lenses with short strike lengths and a more considerable vertical extent.
Cobar Pb-Zn-±Ag mineralisation occurs as individual orebodies predominantly adjacent to, or over parts of earlier formed Cobar Cu-Au(±Zn) systems. The fault/shear hosted Pb-Zn sulphide-rich zones often ‘piggyback’ on the previously formed Cu-Au(±Zn) orebodies (e.g., CSA Mine, Great Cobar Mines) along the major faults on the eastern boundary of the basin. The style of the deposits varies from low-temperature replacement to fault/shear-hosted massive sulphide orebodies with a similar deposit-scale morphology as the Cu-Au-(±Zn) orebodies.
Granite-related Sn-W deposits of the Central Lachlan Orogen form along a 250 km N-NW belt that extends from northern Victoria to the Tallebung region of central NSW. This belt is the second-largest tin field in NSW after New England. These deposits formed outside the Cobar Basin (sensu stricto) and are therefore not included in this study.

2.1. Mineral Prospectivity Mapping in Central Lachlan Orogen Using WofE Method

The WofE approach has been previously used to map mineral prospectivity over the Central Lachlan Orogen area by Kenex Pty Ltd., in colloboration with the Geological Survey of NSW (GSNSW) [31]. The expertise of the GSNSW staff was employed in developing mineral system models for three mineral systems in the central Lachlan Orogen, i.e., (i) Cobar Cu-Au, (ii) Cobar Pb-Zn, and (iii) granite-related Sn-W. The key predictive variables representing different critical ore-forming processes of these mineral systems (i.e., source, transport, trap, and deposition) were determined using these models. Between 138 to 196 predictive maps were developed using the pre-competitive geoscience data from the GSNSW, and analysed for the three mineral system models using the EKD method. Then, spatial data tables were developed by using the information about all the predictive maps, their relevance to the mineral systems and spatial correlation with known mineralisation. Based on multiple criteria (e.g., regional coverage of data, spatial correlation with training points, minimal duplication of predictive map patterns), between 8 to 10 predictive maps were chosen to develop mineral prospectivity maps for these three major mineral systems in the central Lachlan Orogen.

3. Methodology

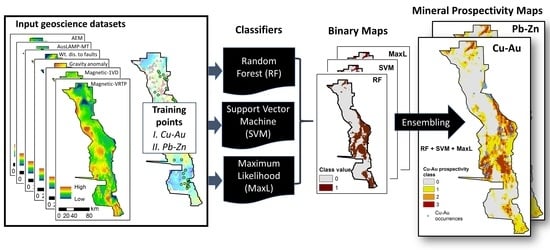
3.1. Overview of the Methodology

A spatial data-driven ensemble machine learning (SDDEML) approach using three supervised learning algorithms, i.e., (i) RF, (ii) SVM and (iii) MaxL, was employed in this study to assess Cobar Cu-Au and Pb-Zn mineral prospectivity using geo-spatial data inputs. The method employed in this study is herein called the SDDEML approach. The produced prospectivity maps were compared against the results of the WofE method (see Section 2.1) and the existing mineral occurrence datasets for validation. ArcGIS 10.8 was used as the main data processing platform in this study.

3.2. Datasets

Data layers that are associated with the mineralisation patterns were chosen as the input datasets. Mineral occurrence points from the NSW MetIndEx database (https://datasets.seed.nsw.gov.au/dataset/nsw-mineral-occurrences, accessed on 1 October 2021) were used as training data in supervised classification. The datasets used in this work, with their sources, are given in Table 1.
The association of gravity and magnetic layers with the mineral occurrences is well established; therefore, these layers were used in testing the many mineral exploration models (e.g., Ref. [36]). The variable reduction to the pole (VRTP) [37] and the first vertical derivative (1VD) magnetic grids [38] with an 80 m cell size obtained from Geoscience Australia were used for this work. Magnetic data provides vital information about the distribution of magnetic minerals in rocks. For example, most sedimentary rocks consist of negligible amounts of magnetic minerals, while igneous and metamorphic rocks consist of appreciable amounts of magnetic minerals. Magnetic data provides valuable information on the boundaries of extensive rock units due to the contrast of magnetic properties between different rocks. These magnetic gradients are enhanced in the derivatives of the total field and can not only map the lithological contacts, but also the fault zones that control fluid flow, and hence the location of many mineral systems.
Gravity anomaly data is commonly used in mineral exploration, considering its variability over different rocks. Gravity anomaly values are higher over the dense rocks compared to the lighter rocks. The Bouguer Anomaly gravity grid of Australia has been developed with airborne gravity/gravity gradiometry data from the National Australian Geophysical Database (NAGD), data from the Australian National Gravity Database (ANGD), and the Global Gravity Grid from National Oceanic and Atmospheric Administration (NOAA) over a 400 m grid [39]. Gravity data can again attribute to, for example, the hidden intrusions with particular shapes that are either less or more dense than the surrounding rocks. Gravity gradients can also show the deep-seated lithospheric structures that many studies have recognised to be the important controlling features of mineral systems [40,41].
The lithospheric-scale structural features can also be mapped by measuring the resistivity of the rocks through the deep looking magnetotelluric method. The Australian Lithospheric Architecture Magnetotelluric (MT) Project (AusLAMP) dataset for NSW [42,43,44,45], which was developed through a collaboration between Geoscience Australia and the GSNSW, was used to assess the deep conductivity/resistivity features that were previously recognised to delineate the corridors and anomalies associated with major mineral systems [46]. This MT dataset is available in an ascii grid format with 285 depth slices (from 2190 m to 337,290 m) over a half degree (~55 km) grid.
Data from an Airborne EM (AEM) survey conducted by Geoscience Australia and the GSNSW, to measure the natural electrical properties of rocks and soil in the Cobar–Lake Cargelligo area, was also used in this work as an input dataset. Electromagnetic surveying can, apart from directly detecting conductive ore minerals, enhance the mapping the lithostructural features in the magnetically quiet regions such as sedimentary basins. Only the footprint of the AEM survey (Figure 1) was chosen as the area of interest (AOI) for this study. This inversion of the AEM dataset consists of 32 depth slices extending from 5 m to 500 m. Currently, the AEM datasets only cover selected parts of Australia and do not provide continent-wide coverage. Therefore, the methodology was tested both with and without the AEM datasets to evaluate their impact on the results when expanding the methodology over other areas in future work.
The mineralisation patterns of the Lachlan Orogen region have a strong association with faults and intrusions [47]. Therefore, the fault attribution geodatabase of the area [35] was also used in this work. The AusMOHO [48,49] and depth to basement data layers [50] were also used as input data, because both the basin morphology and the deep structures that reach the base of the lithosphere could have played a role in the local and regional fluid flow.
The training data for the supervised classification were acquired from the GSNSW MetIndEx mineral occurrence dataset. MetIndex is the mineral occurrence database for NSW, with records of known mineral occurrences across the state. These records have been compiled by the GSNSW, with resource and production data acquired from both historical and current mining operations.

3.3. Data Pre-Processing

As the first step, the input data layers were prepared for the classification process. The datasets were clipped to the extent of the study’ (i.e., the footprint of the Cobar AEM survey) including the gravity anomaly layer, and the magnetic-VRTP and 1VD layers.
The depth to Moho across the Cobar Basin varies from ~26 km to 42 km as per the AusMOHO dataset. A relationship between the MT data and gold mineralisation in western Victoria and south-eastern South Australia was found by Heinson et al. [46] across the low resistivity zone from ~20 km depth to the depth of Moho. Using similar conditions over the Cobar Basin, MT depth slices from 25 km to 42 km across the AOI (11 in total) were extracted. In order to reduce the dataset by choosing the layers exhibiting the highest significance, a principal component analysis (PCA) was applied to the depth slices, and subsequently, covariance and correlation matrices were developed. The first PC demonstrated an accumulated percentage of eigenvalues of 95.2%, which means that a significant portion of the variability of the dataset is captured by this component. The two input MT layers having high loading on the first PC were chosen for the classification process. Similarly, significant AEM layers were chosen after applying a PCA on the AEM depth slices.
The association between the Cu-Au and Pb-Zn mineral occurrences and faults were also considered in selecting the model inputs. The faults over the study area were classified into five separate layers (Figure 2a–e), based on the fault order that is an attribute of the data layer [47]. This association between the mineral occurrences and the faults is seen visually when the MetIndEx mineral occurrence (training) points are overlain on the faults layer (Figure 2a–e). Euclidean distances up to 50 km from the faults were calculated for these layers on a grid with the same size as the magnetic layers. These values were then inverted to have higher values for the pixels closer to the faults and lower values for the pixels far from the faults (Figure 2f–j). Based on the density of the mineral occurrences within a 5 km buffer from the faults, weights varying from 55 to 80 were assigned to each of these five layers. Then, the five weighted layers were combined together by choosing the highest pixel value at each point (Figure 2k). All the input layers were standardised to avoid any bias in classification caused by varied value ranges.
For training the model, ninety-seven Cu-Au and sixty-six Pb-Zn occurrence points over the study area were extracted from the MetIndEx dataset (see Figure 3). Given that the Cobar Basin is extensively explored for mineral occurrences, random negative points were created over the outcropping areas outside a 3 km buffer from the Cu-Au and Pb-Zn occurrence points. The outcropping regions were identified using the ‘depth to basement layer’ (i.e., data gaps or white regions within the depth to basement layer in Figure 3). Over 100 random negative points for Cu-Au and Pb-Zn were generated, separately.

3.4. Classification

The supervised classification algorithms were applied to the magnetic-VRTP, magnetic-1VD, gravity anomaly, MT, distance to faults, and AEM data layers (Figure 4) based on the training points shown in Figure 3. The algorithms were tested both with and without the AEM layer to assess its impact as an input dataset (to take into account that the AEM datasets are not available for all parts of the country).
Three machine learning algorithms, (i) RF, (ii) SVM, and (iii) MaxL, were tested to produce binary maps showing the Cu-Au and Pb-Zn mineral prospectivity. The selection of these algorithms is made by considering their specific strengths and adaptability to the complex challenges posed by mineral mapping. RF’s robustness in handling complex and noisy data, and small sample sizes suits the complex geological and geophysical variations associated with mineral mapping [51]. SVM’s capability to handle both linear and nonlinear relationships [52] aids in classifying the mineral systems based on various properties. MaxL’s probabilistic approach is valuable for estimating the class probabilities and uncertainty [53], which is crucial in providing confidence levels in mineral occurrence predictions. Here, 70% of the data points (Figure 3) were used for training, and 30% for validation. Subsequently, the three binary maps showing the mineral prospectivity (1 for prospective pixels and 0 for non-prospective pixels) for each mineralisation group (i.e., Cu-Au or Pb-Zn) were summed together to identify the regions classified as prospective areas by all three algorithms. i.e.,
M a p F i n a l = M a p R a n d o m _ f o r e s t + M a p S V M + M a p M a x L
where MapFinal is the map showing the combined value of the mineral prospectivity from all three algorithms, and MapRandom_forest, MapSVM, and MapMaxL are the binary values of the mineral prospectivity maps produced by RF, SVM and MaxL algorithms, respectively. The collective integration of these carefully chosen algorithms enables the capture of intricate interrelationships between the input layers and the training data. The summary of this process is illustrated in Figure 5. The possible final pixel values and their mineral prospectivity classification based on the combinations of the resultant binary maps of RF, SVM and MaxL classification are shown in Table 2.
The binary map produced by the MaxL algorithm (MapMaxL) was merged with its confidence (MapMaxL-confidence) of classification using,
M a p M a x L − c l a s s i f i e d = M a p M a x L × M a p M a x L − c o n f i d e n c e
Here, MapMaxL-classified gives the classification confidence of the pixels only in prospective areas.

4. Results

The results of the MaxL classification algorithm-based Cu-Au and Pb-Zn mineral prospectivity mapping are shown in Figure 6 and Figure 7, respectively. Here, panels a and b show the results of the MaxL classification performed by excluding and including the AEM data, respectively. The outputs of the MaxL algorithm-based binary maps (panels a(i) and b(i) of Figure 6 and Figure 7) combined with the classification confidence layers (panels a(ii) and b(ii) of Figure 6 and Figure 7) are shown in panels a(iii) and b(iii) of Figure 6 and Figure 7 (see Equation (2)). Values of 0 in the binary maps show pixels with no mineral prospectivity, whereas values of 1 show prospective pixels. Equation (2) eliminates the areas having 0 values (i.e., no prospectivity) in the final maps. The classification confidence shown in these maps should not be mistaken for the confidence of the mineral prospectivity. However, the classification confidence can indirectly indicate the mineral prospectivity constrained by the input datasets. The areas with high classification confidence (>70%) show a good agreement with the mineral occurrence points (panels a(iii) and b(iii) of Figure 6 and Figure 7). These figures depict that the prospective areas are confined to much smaller regions when the classification algorithm was run, including the AEM data. However, the two output maps produced with and without the AEM data showed similar spatial patterns. Three Cu-Au occurrence points over the northwest region of the AOI have not been well-captured by the MaxL algorithm (Figure 6a(iii),b(iii)). This should be further investigated in detailed explorations.
The prospectivity of Cu-Au and Pb-Zn mineralisation as captured by the three machine learning algorithms, i.e., RF, SVM and MaxL, is shown in Figure 8, Figure 9, Figure 10 and Figure 11. In allcases, the models demonstrated over 80% overall validation accuracy. Figure 8 and Figure 10 show the result of the algorithms tested without the Cobar AEM data as an input, whereas Figure 9 and Figure 11 show the results of the algorithms tested with the Cobar AEM data. In the binary output maps of the RF, SVM and MaxL (panels a–c of Figure 8, Figure 9, Figure 10 and Figure 11), pixels assigned with a class value of 1 (i.e., class-1) show the prospective areas. Pixels assigned with a value of 0 (i.e., class-0) show areas with no prospectivity as per each machine learning algorithm. Panel d shows the combined result of the RF, SVM and MaxL after summing the three binary maps (i.e., panels a–c). The resultant map consists of four pixel values, i.e., 0 to 3 (see Table 1). Pixels captured by all three algorithms as prospective areas are assigned with a value of 3 (i.e., class-3, high prospectivity), pixels captured by only two algorithms as prospective areas are assigned with a value of 2 (i.e., class-2, moderate prospectivity) and pixels captured by prospective areas by only one algorithm are assigned with a value of 1 (i.e., class-1, low prospectivity). Pixels not captured by any of the three algorithms as prospective areas were assigned with a value of 0 (i.e., class 0, no prospectivity).
The prospective regions became confined to slightly smaller regions when the AEM dataset was introduced as an input layer to the classification. However, the mineral prospectivity maps of Cu-Au and Pb-Zn prepared with and without the AEM data show similar spatial patterns.

5. Discussion

5.1. Interpretation and Comparison of Results with Existing Studies

Large areas of the northern- (>~6,560,000 mS) and southern-most (<~6,320,000 mS) parts of the AOI, as well as the eastern and western margins of the central area, have been identified as prospective regions for the Cobar Cu-Au mineral systems. The Cu-Au prospective areas show a general North-South orientation that correlates with the general strike of the major geological units in the Cobar Basin. The results of the Cu-Au prospectivity mapping using the SVM algorithm (Figure 9 and Figure 10) showed a better agreement with the MetIndEx Cu-Au mineral occurrence/training points than the MaxL and RF methods. For example, the Cu-Au occurrences in the northwest of the study area have largely been captured by prospective areas using the SVM-based classification but were not well-captured by the RF and MaxL methods (Figure 8).
Including the AEM data as an input layer for the classification models confined the prospective areas to a slightly smaller extent. However, the classification results without the AEM data showed similar spatial patterns of mineral potential, suggesting that the SDDEML approach tested in this study can be effectively applied over regions where AEM datasets are unavailable.
Class 3 (i.e., highly prospective class where all three algorithms detected a pixel as a prospective area) areas of our Cu-Au mineral prospectivity maps (Figure 12) show a moderate to a strong agreement with the MetIndEx Cu-Au mineral occurrence points. A moderate agreement is observed between class 2 (i.e., pixels where the results of only two algorithms identified them as prospective areas) and the Cu-Au mineral occurrence points. Class 1 (i.e., pixels where the results of only one algorithm identified them as prospective areas) showed a low correlation compared to the MetIndEx data. This implies the robustness of ensembling the three machine learning models to get better results that are less affected by the errors and biases in the individual algorithms.
A moderate to strong agreement was observed between the class 3 (highly prospective) areas of the SDDEML method-based Cu-Au prospectivity maps developed in this study and the prospective areas of the equivalent map produced with the existing WofE approach (Figure 12; Ford et al. [31]—see Section 2.1). A moderate agreement was observed between class 2 of the mineral prospectivity map using the SDDEML approach and the WofE-based results. The agreement between class 1 and the EKD method-based result is less significant.
Importantly, the results of the data-driven-ensemble method presented in this paper showed the Cu-Au prospectivity in the northern- and southern-most parts of the AOI, which were not captured by the WofE approach (Figure 12). Differences in the input data and the algorithms might have caused this disparity. However, it is worth performing a more detailed investigation of these regions to assess any further mineral potential. Using the data-driven SDDEML methods in this study, prospective areas for the Cobar Pb-Zn mineral systems were observed in approximately North-South oriented bands in the AOI’s north-eastern, south-eastern, and southern areas. Notably, many of the predicted prospective areas for the Pb-Zn mineral systems overlap with those for the Cu-Au mineral systems. A possible explanation for this is the documented ‘piggyback’ style of the mineral systems of many mineral occurrences for the Cu-Au and Pb-Zn mineral systems in the Cobar Basin (see Section 2 of this paper and Ford et al. [31]).
The existing EKD method-based mineral prospectivity maps and the data-driven SDDEML method-based mineral prospectivity maps produced by this study showed similar prospectivity patterns across the AOI. There is a strong agreement between the class 3 (highly prospective) areas of the SDDEML method-based Pb-Zn prospectivity maps and the prospective areas of the equivalent map produced by the existing EKD approach (Figure 13). A moderate agreement was observed between class 2 of the mineral prospectivity map using the SDDEML approach and EKD based results. The agreement between class 1 (least prospective) and the EKD method-based result is less significant.
The mineral prospectivity maps produced in this study with the SDDEML methods showed a good agreement with the MetIndEx mineral occurrence (training) points (Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12). This further demonstrates that the SDDEML approach is an effective method to assess the mineral prospectivity of the major mineral systems in the Cobar Basin. The results of ensembling three robust machine learning models (specifically class 3 and 2) showed a better agreement to the results of the WofE method, compared to binary maps produced by using only one model. Although this is a simple approach, ensembling the results makes the SDDEML approach robust in identifying the prospective mineral zones. The results also indicate that the AEM data is not an essential requirement for this analysis; therefore, the SDDEML method could be used to assess mineral prospectivity over other areas where AEM datasets are unavailable.

5.2. Potential Future Work

The results of the spatial data-driven approach in this study are highly encouraging, and the method could be tested in other areas, over different spatial scales, to map the mineral prospectivity using the available geoscience datasets as a preliminary method of investigation. However, it is necessary to conduct a field validation of the results prior to a detailed exploration. When applying this method over other regions, the random negative data points used for training the algorithms could also be collected from drillholes showing no indication of mineralisation. The processing speed of the SDDEML method is much more effective than the more complex and time-consuming knowledge-driven mineral prospectivity mapping methods.
The SDDEML method can be further improved and modified by including different data combinations, classification algorithms, and their combinations. However, it would be worthwhile comparing the results of this method with more complex algorithms such as spatial random forest (e.g., Ref. [36]) and logistic regression methods over a similar AOI to get a better insight into the results. The algorithms for the SDDEML method could also be tested at different depths based on the effective depth resolution/confidence or DOI (depth of investigation) of the different input layers. Although this method should not replace detailed geological investigations, given the speed and simplicity of this data-driven method, the results could be used as an initial assessment and a validation method to compare the results with other mineral prospectivity mapping methods of more poorly investigated areas. Such results can be used as an initial, less biased, guiding step at regional or district scales before performing more detailed geological assessments, such as drilling, and exploration programs at the camp and prospect scales.

6. Conclusions

A spatial data-driven ensemble machine learning (SDDEML) approach was tested in this study to map Cu-Au and Pb-Zn mineral prospectivity in the Cobar Basin of New South Wales, Australia. Three machine-learning approaches, RF, SVM and MaxL, were used in identifying potential deposits and the results were ensembled to achieve maps with higher classification accuracy. Here, magnetic-VRTP, magnetic-1VD, gravity anomaly, distance to faults (weighted), AusLAMP magnetotelluric and, Cobar AEM datasets were used as input data considering their influence on Cu-Au and Pb-Zn mineralisation. Ensembling multiple models provided a better accuracy compared to the individual classification algorithms and provides a more robust approach in mapping mineral prospectivity over different spatial extents. The method was tested using AEM data and without the use of AEM data to examine its potential over areas where AEM data are unavailable. The results indicated that AEM data can somewhat narrow down the extent of mineral prospectivity into slightly smaller regions. The method tested here can be modified and further tested with different combinations of input layers and classification algorithms. The findings of this study are promising for expanding this method over other regions to identify mineral prospectivity with different input datasets. The results of the proposed method can provide an initial assessment and valuable insights for more detailed geological assessments and exploration in prospective mineralised terranes.

Author Contributions

Conceptualization, I.P.S., V.M., A.S.K. and G.R.H.; methodology, I.P.S. and V.M.; validation, I.P.S., C.B.F. and P.L.B.; formal analysis, I.P.S.; resources, A.S.K., G.R.H., A.R.B., C.B.F. and P.L.B.; data curation, I.P.S.; writing—original draft preparation, I.P.S.; writing—review and editing, I.P.S., A.S.K., G.R.H., V.M., C.B.F., P.L.B. and A.R.B.; visualization, I.P.S.; supervision, A.S.K., G.R.H. and V.M.; project administration, V.M. and A.R.B.; funding acquisition, A.S.K. and G.R.H. All authors have read and agreed to the published version of the manuscript.

Funding

The work has been supported by the Mineral Exploration Cooperative Research Centre, whose activities are funded by the Australian Government’s Cooperative Research Centre Program. This is MinEx CRC Document 2023/27. The Article Processing Charges were supported by the Geological Survey of New South Wales.

Data Availability Statement

Sources of the datasets used in this study are provided in the ‘datasets’ section. The final maps are available on request from the corresponding author.

Acknowledgments

We would like to express our gratitude to Giovanni Spampinato from the Geological Survey of New South Wales, Adrian Hitchman from Geoscience Australia, Dave Cole and Hassan Talebi from CSIRO, and other personnel involved with the MinEx CRC project for their assistance and suggestions. Chris Folkes and Phil Blevin publish with the permission of the Executive Director, Geological Survey of New South Wales.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Marjoribanks, R. Geological Methods in Mineral Exploration and Mining; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
  2. Zou, H.; Han, R.; Liu, M.; Cromie, P.; Zaw, K.; Fang, W.; Huang, J.; Ren, T.; Wu, J. Geological, geophysical, and geochemical characteristics of the Ban Kiouchep Cu–Pb–Ag deposit and its exploration significance in Northern Laos. Ore Geol. Rev. 2020, 124, 103603. [Google Scholar] [CrossRef]
  3. Ali, M.A.H.; Mewafy, F.M.; Qian, W.; Alshehri, F.; Ahmed, M.S.; Saleem, H.A. Integration of Electrical Resistivity Tomography and Induced Polarization for Characterization and Mapping of (Pb-Zn-Ag) Sulfide Deposits. Minerals 2023, 13, 986. [Google Scholar] [CrossRef]
  4. Porwal, A.K.; Kreuzer, O.P. Introduction to the special issue: Mineral prospectivity analysis and quantitative resource estimation. Ore Geol. Rev. 2010, 38, 121–127. [Google Scholar] [CrossRef]
  5. Hoover, D.B.; Klein, D.P.; Campbell, D.C.; du Bray, E. Geophysical methods in exploration and mineral environmental investigations. Prelim. Compil. Descr. Geoenviron. Miner. Depos. Models USGS Open-File Rep. 1995, 95, 19–27. [Google Scholar]
  6. Kearey, P.; Brooks, M.; Hill, I. An Introduction to Geophysical Exploration; Wiley-Blackwell: Maldan, MA, USA, 2002; Volume 4. [Google Scholar]
  7. Rose, A.W. Geochemical exploration. In Geochemistry. Encyclopedia of Earth Science; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar]
  8. Grunsky, E.C.; Caritat, P.D. State-of-the-art analysis of geochemical data for mineral exploration. Geochemistry: Exploration, Environment. Analysis 2020, 20, 217–232. [Google Scholar]
  9. Agar, B.; Coulter, D. Remote sensing for mineral exploration—A decade perspective 1997–2007. In Proceedings of the Exploration 07: Fifth Decennial International Conference on Mineral Exploration, Toronto, ON, Canada, 9–12 September 2007; pp. 109–136. [Google Scholar]
  10. Sabins, F.F. Remote sensing for mineral exploration. Ore Geol. Rev. 1999, 14, 157–183. [Google Scholar] [CrossRef]
  11. Shirmard, H.; Farahbakhsh, E.; Müller, R.D.; Chandra, R. A review of machine learning in processing remote sensing data for mineral exploration. Remote Sens. Environ. 2022, 268, 112750. [Google Scholar] [CrossRef]
  12. Lawley, C.J.; Tschirhart, V.; Smith, J.W.; Pehrsson, S.J.; Schetselaar, E.M.; Schaeffer, A.J.; Houlé, M.G.; Eglington, B.M. Prospectivity modelling of Canadian magmatic Ni (±Cu±Co±PGE) sulphide mineral systems. Ore Geol. Rev. 2021, 132, 103985. [Google Scholar] [CrossRef]
  13. Harris, J.; Grunsky, E.; Behnia, P.; Corrigan, D. Data-and knowledge-driven mineral prospectivity maps for Canada’s North. Ore Geol. Rev. 2015, 71, 788–803. [Google Scholar] [CrossRef]
  14. Hosseini, S.A.; Abedi, M. Data envelopment analysis: A knowledge-driven method for mineral prospectivity mapping. Comput. Geosci. 2015, 82, 111–119. [Google Scholar] [CrossRef]
  15. Ma, Y.; Zhao, J.; Sui, Y.; Liao, S.; Zhang, Z. Application of knowledge-driven methods for mineral prospectivity mapping of polymetallic sulfide deposits in the southwest Indian ridge between 46° and 52° E. Minerals 2020, 10, 970. [Google Scholar] [CrossRef]
  16. Carranza, E.J.M.; Laborte, A.G. Data-driven predictive modeling of mineral prospectivity using random forests: A case study in Catanduanes Island (Philippines). Nat. Resour. Res. 2016, 25, 35–50. [Google Scholar] [CrossRef]
  17. Sun, T.; Li, H.; Wu, K.; Chen, F.; Zhu, Z.; Hu, Z. Data-driven predictive modelling of mineral prospectivity using machine learning and deep learning methods: A case study from southern Jiangxi Province, China. Minerals 2020, 10, 102. [Google Scholar] [CrossRef]
  18. Yousefi, M.; Nykänen, V. Data-driven logistic-based weighting of geochemical and geological evidence layers in mineral prospectivity mapping. J. Geochem. Explor. 2016, 164, 94–106. [Google Scholar] [CrossRef]
  19. Fu, C.; Chen, K.; Yang, Q.; Chen, J.; Wang, J.; Liu, J.; Xiang, Y.; Li, Y.; Rajesh, H. Mapping gold mineral prospectivity based on weights of evidence method in southeast Asmara, Eritrea. J. Afr. Earth Sci. 2021, 176, 104143. [Google Scholar] [CrossRef]
  20. Xiong, Y.; Zuo, R. GIS-based rare events logistic regression for mineral prospectivity mapping. Comput. Geosci. 2018, 111, 18–25. [Google Scholar] [CrossRef]
  21. Yuan, F.; Li, X.; Zhang, M.; Jowitt, S.M.; Jia, C.; Zheng, T.; Zhou, T. Three-dimensional weights of evidence-based prospectivity modeling: A case study of the Baixiangshan mining area, Ningwu Basin, Middle and Lower Yangtze Metallogenic Belt, China. J. Geochem. Explor. 2014, 145, 82–97. [Google Scholar] [CrossRef]
  22. Zeghouane, H.; Allek, K.; Kesraoui, M. GIS-based weights of evidence modeling applied to mineral prospectivity mapping of Sn-W and rare metals in Laouni area, Central Hoggar, Algeria. Arab. J. Geosci. 2016, 9, 373. [Google Scholar] [CrossRef]
  23. Brown, W.M.; Gedeon, T.; Groves, D.; Barnes, R. Artificial neural networks: A new method for mineral prospectivity mapping. Aust. J. Earth Sci. 2000, 47, 757–770. [Google Scholar] [CrossRef]
  24. Carranza, E.J.M.; Laborte, A.G. Random forest predictive modeling of mineral prospectivity with small number of prospects and data with missing values in Abra (Philippines). Comput. Geosci. 2015, 74, 60–70. [Google Scholar] [CrossRef]
  25. McKay, G.; Harris, J. Comparison of the data-driven random forests model and a knowledge-driven method for mineral prospectivity mapping: A case study for gold deposits around the Huritz Group and Nueltin Suite, Nunavut, Canada. Nat. Resour. Res. 2016, 25, 125–143. [Google Scholar] [CrossRef]
  26. Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
  27. Zhang, N.; Zhou, K.; Li, D. Back-propagation neural network and support vector machines for gold mineral prospectivity mapping in the Hatu region, Xinjiang, China. Earth Sci. Inform. 2018, 11, 553–566. [Google Scholar] [CrossRef]
  28. Zuo, R. Geodata science-based mineral prospectivity mapping: A review. Nat. Resour. Res. 2020, 29, 3415–3424. [Google Scholar] [CrossRef]
  29. Zuo, R.; Carranza, E.J.M. Support vector machine: A tool for mapping mineral prospectivity. Comput. Geosci. 2011, 37, 1967–1975. [Google Scholar] [CrossRef]
  30. David, V. Cobar Deposits–Structural control. ASEG Ext. Abstr. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
  31. Ford, A.; Peters, K.; Downes, P.; Blevin, P.; Greenfield, J.; Fitzherbert, J. Central Lachlan Orogen Mineral Systems Mineral Systems Report; Report GS2020/0741; Kenex Pty Ltd.: Dongara, WA, Australia, 2020. [Google Scholar]
  32. Folkes, C.B.; Carlton, A.; Eastlake, M.; Deyssing, L.; Trigg, S.; Montgomery, K.; Matthews, S.; Spampinato, G.; Roach, I.; Gilmore, P.; et al. The Cobar AEM Survey Interpretation Report; Report GS2021/1592; Mining, Exploration and Geoscience: Maitland, NSW, Australia, 2022. [Google Scholar]
  33. Glen, R.; Drummond, B.; Goleby, B.; Palmer, D.; Wake-Dyster, K. Structure of the Cobar Basin, New South Wales, based on seismic reflection profiling. Aust. J. Earth Sci. 1994, 41, 341–352. [Google Scholar] [CrossRef]
  34. Seccombe, P.K.; Jiang, Z.; Downes, P.M. Sulfur isotope and fluid inclusion geochemistry of metamorphic Cu–Au deposits, central Cobar area, NSW, Australia. Aust. J. Earth Sci. 2017, 64, 537–556. [Google Scholar] [CrossRef]
  35. Fitzherbert, J.A.; Downes, P.M. A Mineral System Model for Cu-Au-Pb-Zn-Ag Systems of the Cobar Basin, Central Lachlan Orogen, New South Wales 2020; Report GS2021/0042; Regional NSW: Maitland, NSW, Australia, 2020.
  36. Talebi, H.; Peeters, L.J.; Otto, A.; Tolosana-Delgado, R. A truly spatial Random Forests algorithm for geoscience data analysis and modelling. Math. Geosci. 2022, 54, 1–22. [Google Scholar] [CrossRef]
  37. Poudjom Djomani, Y.; Minty, B.R.S. Total Magnetic Intensity (TMI) Grid of Australia with Variable Reduction to Pole (VRTP) 2019, 7th ed.; Geoscience Australia: Canberra, Australia, 2019. [CrossRef]
  38. Poudjom Djomani, Y. Total Magnetic Intensity Grid of Australia 2019—First Vertical Derivative (1VD); Geoscience Australia: Canberra, Australia, 2019. [CrossRef]
  39. Lane, R.J.L.; Wynne, P.E.; Poudjom Djomani, Y.; Stratford, W.R.; Barretto, J.A.; Caratori Tontini, F. 2019 Australian National Gravity Grids: Free Air Anomaly, Complete Bouguer Anomaly, De-Trended Global Isostatic Residual, 400 m Cell Size (Includes Point Located Data); Geoscience Australia: Canberra, Australia, 2020.
  40. McCuaig, T.C.; Beresford, S.; Hronsky, J.M.A. Translating the mineral systems approach into an effective exploration targeting system. Ore Geol. Rev. 2010, 38, 128–138. [Google Scholar] [CrossRef]
  41. Occhipinti, S.; Metelka, V.; Lindsay, M.; Aitken, A.; Pirajno, F.; Tyler, I. The evolution from plate margin to intraplate mineral systems in the Capricorn Orogen, links to prospectivity. Ore Geol. Rev. 2020, 127, 103811. [Google Scholar] [CrossRef]
  42. Kirkby, A.; Musgrave, R.J.; Czarnota, K.; Doublier, M.P.; Duan, J.; Cayley, R.A.; Kyi, D. Lithospheric architecture of a Phanerozoic orogen from magnetotellurics: AusLAMP in the Tasmanides, southeast Australia. Tectonophysics 2020, 793, 228560. [Google Scholar] [CrossRef]
  43. Kirkby, A.L. Resistivity Model of the Southeast Australian Mainland from AusLAMP Magnetotelluric Data; Geoscience Australia: Canberra, Australia, 2020. [CrossRef]
  44. Kyi, D.; Duan, J.; Kirkby, A.L.; Stolz, N. Australian Lithospheric Architecture Magnetotelluric Project (AusLAMP): New South Wales: Data Release (Phase One). Record 2020/011; Geoscience Australia: Canberra, Australia, 2020. [CrossRef]
  45. Robertson, K.; Heinson, G.; Thiel, S. Lithospheric reworking at the Proterozoic–Phanerozoic transition of Australia imaged using AusLAMP Magnetotelluric data. Earth Planet. Sci. Lett. 2016, 452, 27–35. [Google Scholar] [CrossRef]
  46. Heinson, G.; Duan, J.; Kirkby, A.; Robertson, K.; Thiel, S.; Aivazpourporgou, S.; Soyer, W. Lower crustal resistivity signature of an orogenic gold system. Sci. Rep. 2021, 11, 15807. [Google Scholar] [CrossRef] [PubMed]
  47. Folkes, C.B.; Stuart, C. Fault Attribution for the Western Lachlan Orogen of NSW; Report GS2020/0955; Regional NSW: Maitland, NSW, Australia, 2020.
  48. Kennett, B.L.N.; Salmon, M.; Saygin, E.; Group, A.W. AusMoho: The variation of Moho depth in Australia. Geophys. J. Int. 2011, 187, 946–958. [Google Scholar] [CrossRef]
  49. Salmon, M.; Kennett, B.L.N.; Stern, T.; Aitken, A.R.A. The Moho in Australia and New Zealand. Tectonophysics 2013, 609, 288–298. [Google Scholar] [CrossRef]
  50. Stolz, E.; Spampinato, G.; Davidson, J. A statewide 3D geological model for New South Wales. ASEG Ext. Abstr. 2019, 2019, 1–4. [Google Scholar] [CrossRef]
  51. Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
  52. Ghosh, S.; Dasgupta, A.; Swetapadma, A. A Study on Support Vector Machine based Linear and Non-Linear Pattern Classification. In Proceedings of the 2019 International Conference on Intelligent Sustainable Systems (ICISS), Palladam, India, 21–22 February 2019; pp. 24–28. [Google Scholar]
  53. Singh, G.B.; Singh, G.B. Probabilistic Methods: Maximum Likelihood. In Fundamentals of Bioinformatics and Computational Biology: Methods and Exercises in MATLAB; Springer: Cham, Switzerland, 2015; pp. 273–286. [Google Scholar]
Remotesensing 15 04074 g001
Figure 1. Study area, the Central Lachlan Orogen and the Cobar Superbasin, NSW.
Figure 1. Study area, the Central Lachlan Orogen and the Cobar Superbasin, NSW.
Remotesensing 15 04074 g001
Remotesensing 15 04074 g002
Figure 2. (a–e) The classification of faults over the Cobar AEM footprint based on the order of the faults [47]. (f–j) The inverted Euclidean distance from faults for each fault order group. (k) The merged, weighted distance from faults layer.
Figure 2. (a–e) The classification of faults over the Cobar AEM footprint based on the order of the faults [47]. (f–j) The inverted Euclidean distance from faults for each fault order group. (k) The merged, weighted distance from faults layer.
Remotesensing 15 04074 g002
Remotesensing 15 04074 g003
Figure 3. (a) Cu-Au, and (b) Pb-Zn training points used for classification overlaid on the depth to basement layer. The outcropping areas are shown as data gaps (white areas) within the depth to basement layer.
Figure 3. (a) Cu-Au, and (b) Pb-Zn training points used for classification overlaid on the depth to basement layer. The outcropping areas are shown as data gaps (white areas) within the depth to basement layer.
Remotesensing 15 04074 g003
Remotesensing 15 04074 g004
Figure 4. The input layers used for the classification (a) magnetic-VRTP, (b) magnetic-1VD, (c) gravity anomaly, (d) distance to faults (weighted), (e) AusLAMP magnetotelluric, and (f) Cobar AEM data over the Cobar AEM survey footprint.
Figure 4. The input layers used for the classification (a) magnetic-VRTP, (b) magnetic-1VD, (c) gravity anomaly, (d) distance to faults (weighted), (e) AusLAMP magnetotelluric, and (f) Cobar AEM data over the Cobar AEM survey footprint.
Remotesensing 15 04074 g004
Remotesensing 15 04074 g005
Figure 5. The ensemble approach of combining the mineral prospectivity maps produced using RF, SVM, and MaxL algorithms.
Figure 5. The ensemble approach of combining the mineral prospectivity maps produced using RF, SVM, and MaxL algorithms.
Remotesensing 15 04074 g005
Remotesensing 15 04074 g006
Figure 6. Panels (a) and (b), respectively, show the results of the Cu-Au prospectivity mapping tested with MaxL classification by excluding and including the AEM data over the Cobar AEM survey footprint. (a(i)) and (b(i)) show the binary maps showing the Cu-Au prospectivity (i.e., pixel value 1 = prospective and pixel value 0 = no prospectivity), (a(ii)) and (b(ii)) show the classification confidence over the entire area, and (a(iii)) and (b(iii)) shows the Cu-Au prospective areas combined with the classification confidence with the overlain Cu-Au mineral occurrence points.
Figure 6. Panels (a) and (b), respectively, show the results of the Cu-Au prospectivity mapping tested with MaxL classification by excluding and including the AEM data over the Cobar AEM survey footprint. (a(i)) and (b(i)) show the binary maps showing the Cu-Au prospectivity (i.e., pixel value 1 = prospective and pixel value 0 = no prospectivity), (a(ii)) and (b(ii)) show the classification confidence over the entire area, and (a(iii)) and (b(iii)) shows the Cu-Au prospective areas combined with the classification confidence with the overlain Cu-Au mineral occurrence points.
Remotesensing 15 04074 g006
Remotesensing 15 04074 g007
Figure 7. Panels (a) and (b), respectively, show the results of the Pb-Zn prospectivity mapping tested with MaxL classification by including and excluding the AEM data over the Cobar AEM survey footprint. (a(i)) and (b(i)) show the binary maps showing the Pb-Zn prospectivity (i.e., pixel value 1 = prospective and pixel value 0 = no prospectivity), (a(ii)) and (b(ii)) shows the classification confidence over the entire area, and (a(iii)) and (b(iii)) shows the Pb-Zn prospective areas combined with the classification confidence with the overlain Pb-Zn mineral occurrence points.
Figure 7. Panels (a) and (b), respectively, show the results of the Pb-Zn prospectivity mapping tested with MaxL classification by including and excluding the AEM data over the Cobar AEM survey footprint. (a(i)) and (b(i)) show the binary maps showing the Pb-Zn prospectivity (i.e., pixel value 1 = prospective and pixel value 0 = no prospectivity), (a(ii)) and (b(ii)) shows the classification confidence over the entire area, and (a(iii)) and (b(iii)) shows the Pb-Zn prospective areas combined with the classification confidence with the overlain Pb-Zn mineral occurrence points.
Remotesensing 15 04074 g007
Remotesensing 15 04074 g008
Figure 8. Cu-Au prospectivity maps developed with (a) RF, (b) SVM, and (c) MaxL without using Cobar AEM data as an input layer. Class values 1 and 0 show prospective and non-prospective areas, respectively. Map (d) shows the ensembled result after summing (a–c). Class value 3, 2, and 1 depict areas which were captured as prospective areas by (i) all three machine learning algorithms (high confidence), (ii) only two algorithms (moderate confidence), and (iii) only one algorithm (low confidence), respectively. Class value 0 depicts areas that are classified as non-prospective areas by all three algorithms.
Figure 8. Cu-Au prospectivity maps developed with (a) RF, (b) SVM, and (c) MaxL without using Cobar AEM data as an input layer. Class values 1 and 0 show prospective and non-prospective areas, respectively. Map (d) shows the ensembled result after summing (a–c). Class value 3, 2, and 1 depict areas which were captured as prospective areas by (i) all three machine learning algorithms (high confidence), (ii) only two algorithms (moderate confidence), and (iii) only one algorithm (low confidence), respectively. Class value 0 depicts areas that are classified as non-prospective areas by all three algorithms.
Remotesensing 15 04074 g008
Remotesensing 15 04074 g009
Figure 9. Cu-Au prospectivity maps developed with (a) RF, (b) SVM, and (c) MaxL, including Cobar AEM data as an input layer. Class values 1 and 0 show prospective and non-prospective areas, respectively. Map (d) shows the ensembled result after summing (a–c). Class value 3, 2, and 1 depict areas which were captured as prospective areas by (i) all three machine learning algorithms (high confidence), (ii) only two algorithms (moderate confidence), and (iii) only one algorithm (low confidence), respectively. Class value 0 depicts areas that are classified as non-prospective areas by all three algorithms.
Figure 9. Cu-Au prospectivity maps developed with (a) RF, (b) SVM, and (c) MaxL, including Cobar AEM data as an input layer. Class values 1 and 0 show prospective and non-prospective areas, respectively. Map (d) shows the ensembled result after summing (a–c). Class value 3, 2, and 1 depict areas which were captured as prospective areas by (i) all three machine learning algorithms (high confidence), (ii) only two algorithms (moderate confidence), and (iii) only one algorithm (low confidence), respectively. Class value 0 depicts areas that are classified as non-prospective areas by all three algorithms.
Remotesensing 15 04074 g009
Remotesensing 15 04074 g010
Figure 10. Pb-Zn prospectivity maps developed with (a) RF, (b) SVM, and (c) MaxL without using Cobar AEM data as an input layer. Class values 1 and 0 show prospective and non-prospective areas, respectively. Map (d) shows the ensembled result after summing (a–c). Class value 3, 2, and 1 depict areas which were captured as prospective areas by (i) all three machine learning algorithms (high confidence), (ii) only two algorithms (moderate confidence), and (iii) only one algorithm (low confidence), respectively. Class value 0 depicts areas that are classified as non-prospective areas by all three algorithms.
Figure 10. Pb-Zn prospectivity maps developed with (a) RF, (b) SVM, and (c) MaxL without using Cobar AEM data as an input layer. Class values 1 and 0 show prospective and non-prospective areas, respectively. Map (d) shows the ensembled result after summing (a–c). Class value 3, 2, and 1 depict areas which were captured as prospective areas by (i) all three machine learning algorithms (high confidence), (ii) only two algorithms (moderate confidence), and (iii) only one algorithm (low confidence), respectively. Class value 0 depicts areas that are classified as non-prospective areas by all three algorithms.
Remotesensing 15 04074 g010
Remotesensing 15 04074 g011
Figure 11. Cu-Au prospectivity maps developed with (a) RF, (b) SVM, and (c) MaxL, including Cobar AEM data as an input layer. Class values 1 and 0 show prospective and non-prospective areas, respectively. Map (d) shows the ensembled result of summing (a–c). Class value 3, 2, and 1 depict areas which were captured as prospective areas by (i) all three machine learning algorithms (high confidence), (ii) only two algorithms (moderate confidence), and (iii) only one algorithm (low confidence), respectively. Class value 0 depicts areas that are classified as non-prospective areas by all three algorithms.
Figure 11. Cu-Au prospectivity maps developed with (a) RF, (b) SVM, and (c) MaxL, including Cobar AEM data as an input layer. Class values 1 and 0 show prospective and non-prospective areas, respectively. Map (d) shows the ensembled result of summing (a–c). Class value 3, 2, and 1 depict areas which were captured as prospective areas by (i) all three machine learning algorithms (high confidence), (ii) only two algorithms (moderate confidence), and (iii) only one algorithm (low confidence), respectively. Class value 0 depicts areas that are classified as non-prospective areas by all three algorithms.
Remotesensing 15 04074 g011
Remotesensing 15 04074 g012
Figure 12. Comparison between the Cu-Au prospectivity mapping results from the (a) ensemble data-driven approach (this study), and (b) the WofE approach used by GSNSW [31].
Figure 12. Comparison between the Cu-Au prospectivity mapping results from the (a) ensemble data-driven approach (this study), and (b) the WofE approach used by GSNSW [31].
Remotesensing 15 04074 g012
Remotesensing 15 04074 g013
Figure 13. Comparison between the Pb-Zn prospectivity mapping results from the (a) ensemble data-driven approach (this study), and (b) the WofE approach used by GSNSW [31].
Figure 13. Comparison between the Pb-Zn prospectivity mapping results from the (a) ensemble data-driven approach (this study), and (b) the WofE approach used by GSNSW [31].
Remotesensing 15 04074 g013
Table 1. Datasets used in this study.
Table 1. Datasets used in this study.
DatasetSource
Total Magnetic Intensity with variable reduction to the pole (VRTP)Geoscience Australia
https://ecat.ga.gov.au/geonetwork/srv/eng/catalog.search#/metadata/131519, accessed on 5 August 2021
Total Magnetic Intensity–First Vertical Derivative (1VD)Geoscience Australia
https://ecat.ga.gov.au/geonetwork/srv/eng/catalog.search#/metadata/132275, accessed on 5 August 2021
Gravity anomalyGeoscience Australia
https://ecat.ga.gov.au/geonetwork/srv/eng/catalog.search#/metadata/133023, accessed on 5 August 2021
The Australian Lithospheric Architecture Magnetotelluric Project (AusLAMP) dataGeoscience Australia
https://ecat.ga.gov.au/geonetwork/srv/eng/catalog.search#/metadata/131889, accessed on 20 August 2021
Cobar AEM dataGSNSW and Geoscience Australia
https://minview.geoscience.nsw.gov.au/#/(dlmodal:geophys-survey-air/AIR0759)?lon=148.5&lat=-32.5&z=7&bm=bm1&l=gp118:y:100, accessed on 30 July 2021
Fault attribution of Zone 55WGSNSW
AusMOHOAustralian Passive Seismic Server (AusPass) and the Australian National University Data Commons
http://rses.anu.edu.au/seismology/AuSREM/AusMoho, accessed on 10 October 2021
Depth to basementGSNSW
https://geonetwork.geoscience.nsw.gov.au/geonetwork/srv/eng/catalog.search#/metadata/97772139-31b0-412b-ab0a-86a6b2f66c2d, accessed on 20 August 2021
Mineral Occurrence (NSW MetIndEx) dataGSNSW
http://portal.auscope.org.au/geonetwork/srv/eng/catalog.search#/metadata/fd59b712f10394e68f07261981ac6d771d72aacd, accessed on 1 October 2021
Table 2. The possible pixel values of the map showing the summed value of the RF-, SVM-, and MaxL-based binary mineral prospectivity maps.
Table 2. The possible pixel values of the map showing the summed value of the RF-, SVM-, and MaxL-based binary mineral prospectivity maps.
Pixel ValueMineral
Prospectivity
MapRandom_ForestMapSVMMAPMaxLFinal Map
0000None
1001Low
0101
0011
1102Moderate
0112
1012
1113High
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Senanayake, I.P.; Kiem, A.S.; Hancock, G.R.; Metelka, V.; Folkes, C.B.; Blevin, P.L.; Budd, A.R. A Spatial Data-Driven Approach for Mineral Prospectivity Mapping. Remote Sens. 2023, 15, 4074. https://doi.org/10.3390/rs15164074

AMA Style

Senanayake IP, Kiem AS, Hancock GR, Metelka V, Folkes CB, Blevin PL, Budd AR. A Spatial Data-Driven Approach for Mineral Prospectivity Mapping. Remote Sensing. 2023; 15(16):4074. https://doi.org/10.3390/rs15164074

Chicago/Turabian Style

Senanayake, Indishe P., Anthony S. Kiem, Gregory R. Hancock, Václav Metelka, Chris B. Folkes, Phillip L. Blevin, and Anthony R. Budd. 2023. "A Spatial Data-Driven Approach for Mineral Prospectivity Mapping" Remote Sensing 15, no. 16: 4074. https://doi.org/10.3390/rs15164074

APA Style

Senanayake, I. P., Kiem, A. S., Hancock, G. R., Metelka, V., Folkes, C. B., Blevin, P. L., & Budd, A. R. (2023). A Spatial Data-Driven Approach for Mineral Prospectivity Mapping. Remote Sensing, 15(16), 4074. https://doi.org/10.3390/rs15164074

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop