Strong-Scattering Multiparameter Reconstruction Based on Elastic Direct Envelope Inversion and Full-Waveform Inversion with Anisotropic Total Variation Constraint
Abstract
:1. Introduction
2. Review of Elastic Full-Waveform Inversion and Direct Envelope Inversion
2.1. Elastic Full-Waveform Inversion (EFWI)
2.2. Elastic Direct Envelope Inversion (EDEI)
3. EDEI with Anisotropic Total Variation Constraint (EDEI-ATV)
3.1. Anisotropic Total Variation (ATV) Constraint
3.2. EDEI with ATV Constraint (EDEI-ATV)
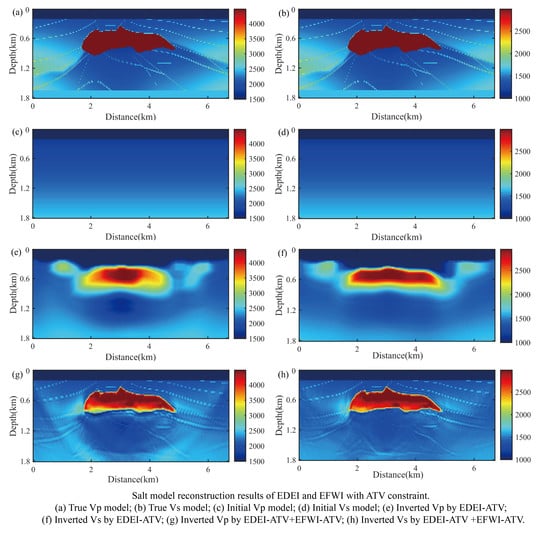
4. Numerical Examples
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tarantola, A. Inversion of seismic reflection data in the acoustic approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Virieux, J.; Operto, S. An overview of full-waveform inversion in exploration geophysics. Geophysics 2009, 74, WCC127–WCC152. [Google Scholar] [CrossRef]
- Rivera, C.; Trinh, P.; Bergounioux, E.; Duquet, B. Elastic multiparameter FWI in sharp contrast medium. In Proceedings of the 89th SEG Annual Meeting, San Antonio, TX, USA, 15–20 September 2019. [Google Scholar]
- Shin, C.; Cha, Y.H. Waveform inversion in the Laplace domain. Geophys. J. Int. 2008, 173, 922–931. [Google Scholar] [CrossRef] [Green Version]
- Shin, C.; Cha, Y.H. Waveform inversion in the Laplace-Fourier domain. Geophys. J. Int. 2009, 177, 1067–1079. [Google Scholar] [CrossRef]
- Lewis, W.; Starr, B.; Vigh, D. A level set approach to salt geometry inversion in full-waveform inversion. In Proceedings of the 82nd SEG Annual Meeting, Las Vegas, NV, USA, 4–9 November 2012. [Google Scholar]
- Chen, S.; Chen, G. Full waveform inversion based on time-integral-damping wavefield. J. Appl. Geophys. 2019, 163, 84–95. [Google Scholar] [CrossRef]
- Yang, F.; Ma, J. Deep-learning inversion: A next-generation seismic velocity model building method. Geophysics 2019, 84, R583–R599. [Google Scholar] [CrossRef] [Green Version]
- Anagaw, A.; Sacchi, M. Edge-preserving smoothing for simultaneous-source full-waveform inversion model updates in high-contrast velocity models. Geophysics 2018, 83, A33–A37. [Google Scholar] [CrossRef]
- Chai, X.; Tang, G.; Peng, R.; Liu, S. The linearized Bregman method for frugal full-waveform inversion with compressive sensing and sparsity-promoting. Pure Appl. Geophys. 2018, 175, 1085–1101. [Google Scholar] [CrossRef]
- Askan, A.; Akcelik, V.; Bielak, J.; Ghattas, O. Full waveform inversion for seismic velocity and anelastic losses in heterogeneous structures. Bull. Seismol. Soc. Amer. 2007, 97, 1990–2008. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Huang, L. Acoustic- and elastic-waveform inversion using a modified total-variation regularization scheme. Geophys. J. Int. 2015, 200, 489–502. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Han, L.; Gong, X.; Sun, H.; Mao, B. Multi-source elastic full waveform inversion based on the anisotropic total variation constraint. Chin. J. Geophys. -Chin. Ed. 2018, 61, 716–732. [Google Scholar]
- Qu, S.; Verschuur, E.; Chen, Y. Full-waveform inversion and joint migration inversion with an automatic directional total variation constraint. Geophysics 2019, 84, R175–R183. [Google Scholar] [CrossRef]
- Aghamiry, H.; Gholami, A.; Operto, S. Multiparameter wavefield reconstruction inversion for wavespeed and attenuation with bound constraints and total variation regularization. Geophysics 2020, 85, R381–R396. [Google Scholar]
- Feng, D.; Wang, X.; Wang, X. New dynamic stochastic source encoding combined with a minmax-concave total variation regularization strategy for full waveform inversion. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7753–7771. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, J.; Innanen, K.A.; Trad, D.O. A recurrent neural network for 1 anisotropic viscoelastic full waveform inversion with high-order total variation regularization. In Proceedings of the First International Meeting for Applied Geoscience & Energy, Denver, CO, USA, 27 August–1 September 2021. [Google Scholar]
- Esser, E.; Herrmann, F.J.; Guasch, L.; Warner, M. Constraint waveform inversion in salt-affected datasets. In Proceedings of the 85th SEG Annual Meeting, New Orleans, LA, USA, 18–23 October 2015. [Google Scholar]
- Esser, E.; Guasch, L.; Herrmann, F.J.; Warner, M. Constrained waveform inversion for automatic salt flooding. Lead. Edge 2016, 35, 235–239. [Google Scholar] [CrossRef]
- Qiu, L.; Chemingui, N.; Zou, Z.; Valenciano, A. Full waveform inversion with steerable variation regularization. In Proceedings of the 86th SEG Annual Meeting, Dallas, TX, USA, 16–21 October 2016. [Google Scholar]
- Peters, B.; Herrmann, F.J. Constraints versus penalties for edge-preserving full-waveform inversion. Lead. Edge 2017, 36, 94–100. [Google Scholar] [CrossRef]
- Yong, P.; Liao, W.; Huang, J.; Li, Z. Total variation regularization for seismic waveform inversion using an adaptive primal dual hybrid gradient method. Inverse Probl. 2018, 34, 045006. [Google Scholar] [CrossRef]
- Kalita, M.; Kazei, V.; Choi, Y.; Alkhalifah, T. Regularized full-waveform inversion with automated salt flooding. Geophysics 2019, 84, R569–R582. [Google Scholar] [CrossRef] [Green Version]
- Wu, R.S.; Luo, J.; Wu, B. Seismic envelope inversion and modulation signal model. Geophysics 2014, 79, WA13–WA24. [Google Scholar] [CrossRef]
- Luo, J.R.; Wu, R.S. Seismic envelope inversion: Reduction of local minima and noise resistance. Geophys. Prospect. 2015, 63, 597–614. [Google Scholar] [CrossRef]
- Bozdag, E.; Trampert, J.; Tromp, J. Misfit functions for full waveform inversion based on instantaneous phase and envelope measurements. Geophys. J. Int. 2011, 185, 845–870. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, R.S.; Han, L. Seismic envelope inversion based on hybrid scale separation for data with strong noises. Pure Appl. Geophys. 2019, 176, 165–188. [Google Scholar] [CrossRef]
- Wu, R.S.; Chen, G. New Fréchet derivative for envelope data and multi-scale envelope inversion. In Proceedings of the 79th EAGE Annual Meeting, Paris, France, 12–15 June 2017. [Google Scholar]
- Wu, R.S.; Chen, G. Multi-Scale Seismic Envelope Inversion Using a Direct Envelope Fréchet Derivative for Strong-Nonlinear Full Waveform Inversion. 2018. Available online: https://arxiv.org/abs/1808.05275 (accessed on 20 November 2022).
- Wu, R.S. Towards a Theoretical Background for Strong-Scattering Inversion—Direct Envelope Inversion and Gel’fand-Levitan-Marchenko Theory. Commun. Comput. Phys. 2020, 28, 41–73. [Google Scholar]
- Chen, G.; Wu, R.S.; Chen, S. Reflection multi-scale envelope inversion. Geophys. Prospect. 2018, 66, 1258–1271. [Google Scholar] [CrossRef]
- Chen, G.; Wu, R.S.; Wang, Y.; Chen, S. Multi-scale signed envelope inversion. J. Appl. Geophys. 2018, 153, 113–126. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, R.S.; Chen, G.; Peng, Z. Seismic modulation model and envelope inversion with smoothed apparent polarity. J. Geophys. Eng. 2018, 15, 2278–2286. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Yang, W.; Chen, S.; Liu, Y.; Gu, Z. Application of envelope in salt structure velocity building: From objective function construction to the full-band seismic data reconstruction. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6594–6608. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, R.S.; Han, L. Source-independent seismic envelope inversion based on the direct envelope Fréchet derivative. Geophysics 2018, 83, R581–R595. [Google Scholar] [CrossRef]
- Chen, G.; Wu, R.S.; Chen, S. Multiscale direct envelope inversion: Algorithm and methodology for application to the salt structure inversion. Earth Space Sci. 2019, 6, 174–190. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Wu, R.S.; Han, L.; Zhang, P. Joint multiscale direct envelope inversion of phase and amplitude in the time-frequency domain. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5108–5120. [Google Scholar] [CrossRef]
- Luo, J.; Wu, R.S.; Chen, G. Angle domain direct envelope inversion method for strong-scattering velocity and density estimation. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1508–1512. [Google Scholar] [CrossRef]
- Zhang, P.; Han, L.; Zhang, F.; Feng, Q.; Chen, X. Wavefield decomposition-based direct envelope inversion and structure-guided perturbation decomposition for salt building. Minerals 2021, 11, 919. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, R.S.; Han, L.; Hu, Y. Elastic direct envelope inversion based on wave mode decomposition for multi-parameter reconstruction of strong-scattering media. Pet. Sci. 2022, 19, 2046–2063. [Google Scholar] [CrossRef]
- Luo, J.; Wu, R.S.; Hu, Y.; Chen, G. Strong scattering elastic full waveform inversion with the envelope Fréchet derivative. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8008805. [Google Scholar] [CrossRef]
- Chen, G.; Yang, W.; Liu, Y.; Wang, H.; Huang, X. Salt structure elastic full waveform inversion based on the multiscale signed envelope. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Zhang, P.; Xing, Z.; Hu, Y. Velocity construction using active and passive multi-component seismic data based on elastic full waveform inversion. Chin. J. Geophys. -Chin. Ed. 2019, 62, 3974–3987. [Google Scholar]
- Beck, A.; Teboulle, M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar] [CrossRef] [Green Version]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Wu, R.-S.; Han, L.; Zhou, Y. Strong-Scattering Multiparameter Reconstruction Based on Elastic Direct Envelope Inversion and Full-Waveform Inversion with Anisotropic Total Variation Constraint. Remote Sens. 2023, 15, 746. https://doi.org/10.3390/rs15030746
Zhang P, Wu R-S, Han L, Zhou Y. Strong-Scattering Multiparameter Reconstruction Based on Elastic Direct Envelope Inversion and Full-Waveform Inversion with Anisotropic Total Variation Constraint. Remote Sensing. 2023; 15(3):746. https://doi.org/10.3390/rs15030746
Chicago/Turabian StyleZhang, Pan, Ru-Shan Wu, Liguo Han, and Yixiu Zhou. 2023. "Strong-Scattering Multiparameter Reconstruction Based on Elastic Direct Envelope Inversion and Full-Waveform Inversion with Anisotropic Total Variation Constraint" Remote Sensing 15, no. 3: 746. https://doi.org/10.3390/rs15030746
APA StyleZhang, P., Wu, R. -S., Han, L., & Zhou, Y. (2023). Strong-Scattering Multiparameter Reconstruction Based on Elastic Direct Envelope Inversion and Full-Waveform Inversion with Anisotropic Total Variation Constraint. Remote Sensing, 15(3), 746. https://doi.org/10.3390/rs15030746