A Three-Dimensional Block Adjustment Method for Spaceborne InSAR Based on the Range-Doppler-Phase Model
Abstract
:1. Introduction
2. Analysis of the Range-Doppler-Phase Model
2.1. Range-Doppler-Phase Model
2.2. Analysis for RDP Model
2.2.1. Spatial Baseline
2.2.2. Slant Range
2.2.3. Orbit and Timing Parameter
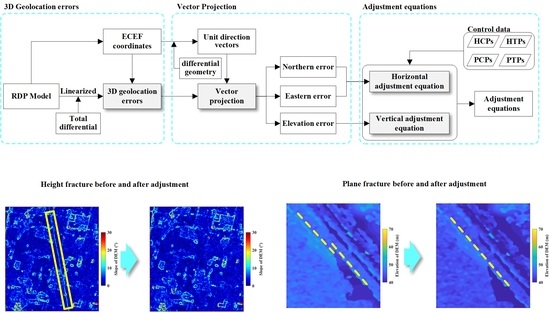
3. Method
3.1. Three-Dimensional Geolocation Error Equation
3.2. Adjustment Equations of Various Control Data
3.2.1. Equation of HCPs
3.2.2. Equation of PCPs
3.2.3. Equation of HTPs
3.2.4. Equation of PTPs
3.3. Solution Strategy
- i.
- Initialize adjustment parameter , i.e., .
- ii.
- Set tolerance limits , , and for the increment of baseline, range, and timing parameters. According to the analysis in Section 2, , , and should be below millimeters, meters, and 0.1 milliseconds, respectively. For example, mm, m, and ms.
- iii.
- iv.
- Sperate the corrections of slant range, azimuth time, and spatial baseline according to their track, add the corrections to the result of the previous iteration, i.e., , to update the range, timing, and baseline parameters.
- v.
- Judge whether the increment of each parameter is less than the tolerance limit. If less than, end iterative calculation and take as the solution of adjustment parameters. Otherwise, re-execute step iii.
4. Experiment and Discussion
4.1. Experiment Data
4.2. Simulated Experiment
- i.
- Generate absolute interferometric phase. We select the external DEM in the experimental area as the simulated terrain and the geometric parameters of InSAR data, such as orbit and baseline, as the accurate geometric parameters. The absolute interferometric phase is calculated through the reverse geolocation method.
- ii.
- Generate checkpoints and control points. We select a series of geographic points in the simulated terrain, part of which are checkpoints, and the other points are added with Gaussian white noise as the HCPs and PCPs, respectively.
- iii.
- Generate DEMs. We add systematic error into baseline, slant range, and timing parameters and then generate DEMs according to the strict model Equation (1). Then, we determined the observation values of heights corresponding to HCPs and PCPs extracted in step ii.
- iv.
- Extract tie points. As described in Section 3.2.3 and Section 3.2.4, HTPs can be selected by the geolocation method, while PTPs need to be extracted by matching methods.
- v.
- Adjust and verify accuracy. Unlike the real data experiment, the accuracy verification of the simulated experiment includes not only the plane and elevation accuracies of adjusted DEMs but also the difference between the simulated error and the adjustment calculation value. The latter is used to verify whether the proposed method can accurately calculate the systematic errors of bistatic InSAR systems.
4.3. Real-Data Experiment
4.3.1. Fracture in DEM Mosaic Maps
4.3.2. Adjustment Effect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| InSAR | Synthetic aperture radar interferometry |
| CoSSC | Co-registered Single look Slant range Complex |
| DEM | Digital Elevation Model |
| RDP | Range-Doppler-Phase |
| HCP | Height control point |
| HTP | Height tie point |
| PCP | Plane control point |
| PTP | Plane tie point |
Appendix A. Derivation of the North, East and Upper Unit Vectors in the ECEF Coordinate System

Appendix B. Deduction of Adjustment Equations
Appendix B.1. Derivation of the Total Differential Form of the RDP Model
Appendix B.2. The Concrete Form of Design Matrixes in Adjustment Equations
References
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Kampes, B.M. Radar Interferometry; Springer: Berlin/Heidelberg, Germany, 2006; Volume 12. [Google Scholar]
- Pitz, W.; Miller, D. The TerraSAR-X satellite. IEEE Trans. Geosci. Remote Sens. 2010, 48, 615–622. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A satellite formation for high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Wessel, B.; Gruber, A.; Huber, M.; Roth, A. TanDEM-X: Block adjustment of interferometric height models. In Proceedings of the ISPRS Hannover Workshop 2009 “High-Resolution Earth Imaging for Geospatioal Information”, International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Hannover, Germany, 2–5 June 2009; pp. 1–6. [Google Scholar]
- Xijuan, Y.; Chunming, H.; Changyong, D.; Yinghui, Z. Mathematical model of airborne InSAR block adjustment. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 59–63. [Google Scholar]
- Gruber, A.; Wessel, B.; Huber, M.; Roth, A. Operational TanDEM-X DEM calibration and first validation results. ISPRS J. Photogramm. Remote Sens. 2012, 73, 39–49. [Google Scholar] [CrossRef]
- Ma, J.; You, H.J.; Hu, D.H. Block adjustment of InSAR images based on the combination of F. Leberl and interferometric models. J. Infrared Millim. Waves 2012, 31, 271–276. [Google Scholar] [CrossRef]
- González, J.H.; Bachmann, M.; Scheiber, R.; Andres, C.; Krieger, G. TanDEM-X DEM calibration and processing experiments with E-SAR. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 3, p. 115. [Google Scholar]
- Sansosti, E. A simple and exact solution for the interferometric and stereo SAR geolocation problem. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1625–1634. [Google Scholar] [CrossRef]
- Duque, S.; Balss, U.; Rossi, C.; Fritz, T.; Balzer, W. TanDEM-X Payload Ground Segment, CoSSC Generation and Interferometric Considerations; German Aerospace Center: Oberpfaffenhofen, Germany, 2012. [Google Scholar]
- González, J.H.; Bachmann, M.; Krieger, G.; Fiedler, H. Development of the TanDEM-X calibration concept: Analysis of systematic errors. IEEE Trans. Geosci. Remote Sens. 2009, 48, 716–726. [Google Scholar] [CrossRef]
- Huber, M.; Gruber, A.; Wessel, B.; Breunig, M.; Wendleder, A. Validation of tie-point concepts by the DEM adjustment approach of TanDEM-X. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2644–2647. [Google Scholar]
- Wessel, B. TanDEM-X Ground Segment–DEM Products Specification Document; Deutsches Zentrum fur Luft- und Raumfahrt: Koln, Germany, 2018. [Google Scholar]
- Mallorqui, J.J.; Bara, M.; Broquetas, A. Calibration requirements for airborne SAR interferometry. SAR Image Anal. Model. Tech. SPIE 2000, 4173, 267–278. [Google Scholar]
- Jin, G.; Xiong, X.; Xu, Q.; Gong, Z.; Zhou, Y. Baseline Estimation Algorithm with Block Adjustment for Multi-Pass Dual-Antenna Insar. In Proceedings of the The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; pp. 39–45. [Google Scholar]
- Qingsong, W. Research on High-Efficiency and High-Precision Processing Techniques of Spaceborne Interferometric Synthetic Aperture Radar. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2011. [Google Scholar]
- Yanping, W.; Hailiang, P. Locating calibrators in airborne InSAR calibration. In Proceedings of the IGARSS 2003—2003 IEEE International Geoscience and Remote Sensing Symposium (IEEE Cat. No. 03CH37477), Toulouse, France, 21–25 July 2003; Volume 7, pp. 4515–4517. [Google Scholar]
- Lu, L.; Huang, G. A Single-Pass Airborne Interferometric Calibration Method Research For DEM Mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 331–336. [Google Scholar] [CrossRef]
- Li, Y.W.; Xiang, M.S.; Lü, X.L.; Wei, L.D. Joint interferometric calibration based on block adjustment for an airborne dual-antenna InSAR system. Int. J. Remote Sens. 2014, 35, 6444–6468. [Google Scholar] [CrossRef]
- Curlander, J.C. Location of spaceborne SAR imagery. IEEE Trans. Geosci. Remote. Sens. 1982, 20, 359–364. [Google Scholar] [CrossRef]
- González, J.H.; Antony, J.M.W.; Bachmann, M.; Krieger, G.; Zink, M.; Schrank, D.; Schwerdt, M. Bistatic system and baseline calibration in TanDEM-X to ensure the global digital elevation model quality. ISPRS J. Photogramm. Remote Sens. 2012, 73, 3–11. [Google Scholar] [CrossRef]
- Wermuth, M.; Konig, R.; Moon, Y.; Antony, J.W.; Montenbruck, O. Two Years of TanDEM-X Baseline Determination. Int. J. Space Sci. Eng. 2014, 2, 35–48. [Google Scholar] [CrossRef]
- Antony, J.W.; Gonzalez, J.H.; Schwerdt, M.; Bachmann, M.; Krieger, G.; Zink, M. Results of the TanDEM-X baseline calibration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1495–1501. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Y.; Fu, H.; Zhu, J.; Yu, Y.; Li, R.; Zhang, S.; Qu, Z.; Hu, S. Parameterized Modeling and Calibration for Orbital Error in TanDEM-X Bistatic SAR Interferometry over Complex Terrain Areas. Remote Sens. 2021, 13, 5124. [Google Scholar] [CrossRef]
- Liangsheng, L.; Zhiming, L.; Hao, Z.; Fangming, Q.; Yan, H. TH-2 satellite engineering design and implementation. Acta Geod. Cartogr. Sin. 2020, 49, 1252. [Google Scholar]
- Lu, H.; Suo, Z.; Li, Z.; Xie, J.; Zhao, J.; Zhang, Q. InSAR baseline estimation for Gaofen-3 real-time DEM generation. Sensors 2018, 18, 2152. [Google Scholar] [CrossRef] [PubMed]
- Eineder, M.; Minet, C.; Steigenberger, P.; Cong, X.; Fritz, T. Imaging geodesy—Toward centimeter-level ranging accuracy with TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2010, 49, 661–671. [Google Scholar] [CrossRef]
- Yunjun, Z.; Fattahi, H.; Pi, X.; Rosen, P.; Simons, M.; Agram, P.; Aoki, Y. Range Geolocation Accuracy of C-/L-Band SAR and its Implications for Operational Stack Coregistration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Breit, H.; Fritz, T.; Balss, U.; Lachaise, M.; Niedermeier, A.; Vonavka, M. TerraSAR-X SAR processing and products. IEEE Trans. Geosci. Remote Sens. 2009, 48, 727–740. [Google Scholar] [CrossRef]
- Chibiao, D.; Jiayin, L.; Bin, L.; Xiaolan, Q. Preliminary exploration of systematic geolocation accuracy of GF-3 SAR satellite system. J. Radars 2017, 6, 11–16. [Google Scholar]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat mission. Geophys. Res. Lett. 2005, 32, GL024009. [Google Scholar] [CrossRef]
- Li, Z.; Bethel, J. DEM registration, alignment and evaluation for SAR interferometry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 11–116. [Google Scholar]
- Ravanbakhsh, M.; Fraser, C. DEM registration based on mutual information. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Melbourne, Australia, 25 August–1 September 2012. [Google Scholar]
- Suri, S.; Reinartz, P. Mutual-information-based registration of TerraSAR-X and Ikonos imagery in urban areas. IEEE Trans. Geosci. Remote Sens. 2009, 48, 939–949. [Google Scholar] [CrossRef]
- Kennedy, R.; Cohen, W. Automated designation of tie-points for image-to-image coregistration. Int. J. Remote Sens. 2003, 24, 3467–3490. [Google Scholar] [CrossRef]
- Teo, T.A.; Chen, L.C.; Liu, C.L.; Tung, Y.C.; Wu, W.Y. DEM-aided block adjustment for satellite images with weak convergence geometry. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1907–1918. [Google Scholar]
- Zhang, G.; Wang, T.y.; Li, D.; Tang, X.; Jiang, Y.h.; Huang, W.c.; Pan, H. Block adjustment for satellite imagery based on the strip constraint. IEEE Trans. Geosci. Remote Sens. 2014, 53, 933–941. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tian, X.; Shan, J. Comprehensive evaluation of the ICESat-2 ATL08 terrain product. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8195–8209. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Error analysis on grid-based slope and aspect algorithms. Photogramm. Eng. Remote Sens. 2004, 70, 957–962. [Google Scholar] [CrossRef]
















| Parameters | Values |
|---|---|
| Slant range (km) | 682.70 |
| Satellite position (km) | (−2706.04, 5088.03, 3765.30) |
| Satellite velocity (m/s) | (−524.50, 4389.90, −6288.98) |
| Baseline vector (m) | (0.62, −266.42, 430.36) |
| Absolute interferometric phase (rad) | −174.18 |
| Target coordinate (km) | (−2070.03, 4915.39, 3486.46) |
| Eastern unit vector (m) | (−0.91, −0.42, 0.0) |
| Northern unit vector (m) | (0.23, −0.51, 0.83) |
| Upper unit vector (m) | (−0.35, 0.75, 0.56) |
| Time | Orbit | Incidence () | Resolution (m) | Baseline Length (m) |
|---|---|---|---|---|
| 26 January 2012 | ASC | 33.63 | 1.34 × 1.98 | 506.15 |
| 6 February 2012 | ASC | 34.16 | 1.36 × 2.03 | 577.90 |
| 17 February 2012 | ASC | 33.58 | 1.36 × 2.19 | 607.98 |
| 2 November 2012 | ASC | 33.91 | 1.36 × 2.04 | 485.38 |
| 5 December 2012 | ASC | 33.86 | 1.36 × 1.99 | 657.02 |
| 16 December 2012 | ASC | 33.83 | 1.36 × 1.71 | 612.14 |
| 24 July 2013 | ASC | 33.95 | 1.36 × 1.85 | 559.86 |
| 27 January 2018 | DEC | 34.27 | 1.36 × 2.19 | 479.02 |
| 27 February 2019 | DEC | 38.35 | 1.36 × 1.83 | 459.50 |
| 10 March 2019 | DEC | 33.72 | 1.36 × 1.98 | 480.65 |
| Data | Range (m) | Timing (ms) | Basline Offset (mm) |
|---|---|---|---|
| 26 January 2012 | 5.47 | 0.109 | 2.03 |
| 6 February 2012 | 4.40 | 0.054 | 1.51 |
| 17 February 2012 | 5.42 | −0.28 | 2.34 |
| 2 November 2012 | 2.01 | −0.641 | 1.99 |
| 5 December 2012 | −14.84 | −0.459 | 1.26 |
| 16 December 2012 | 0.75 | −0.040 | 0.25 |
| 24 July 2013 | 2.61 | 1.40 | 0.10 |
| 27 January 2018 | 2.47 | 0.937 | 2.12 |
| 27 February 2019 | 1.87 | 0.540 | 0.20 |
| 10 March 2019 | 0.95 | 0.734 | 1.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Lv, X.; Chai, H.; Zhang, L. A Three-Dimensional Block Adjustment Method for Spaceborne InSAR Based on the Range-Doppler-Phase Model. Remote Sens. 2023, 15, 1046. https://doi.org/10.3390/rs15041046
Wang R, Lv X, Chai H, Zhang L. A Three-Dimensional Block Adjustment Method for Spaceborne InSAR Based on the Range-Doppler-Phase Model. Remote Sensing. 2023; 15(4):1046. https://doi.org/10.3390/rs15041046
Chicago/Turabian StyleWang, Rui, Xiaolei Lv, Huiming Chai, and Li Zhang. 2023. "A Three-Dimensional Block Adjustment Method for Spaceborne InSAR Based on the Range-Doppler-Phase Model" Remote Sensing 15, no. 4: 1046. https://doi.org/10.3390/rs15041046
APA StyleWang, R., Lv, X., Chai, H., & Zhang, L. (2023). A Three-Dimensional Block Adjustment Method for Spaceborne InSAR Based on the Range-Doppler-Phase Model. Remote Sensing, 15(4), 1046. https://doi.org/10.3390/rs15041046