Next Article in Journal
A Nonlinear Grid Transformation Method for Extrapolating and Predicting the Convective Echo of Weather Radar
Previous Article in Journal
Inferences on the 2021 Ongoing Volcanic Unrest at Vulcano Island (Italy) through a Comprehensive Multidisciplinary Surveillance Network
Previous Article in Special Issue
Generalized Additive Model Reveals Nonlinear Trade-Offs/Synergies between Relationships of Ecosystem Services for Mountainous Areas of Southwest China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 5
10.3390/rs15051404
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Performance of Multiple Models for Estimating Rodent Activity Intensity in Alpine Grassland Using Remote Sensing

by
Guang Dong
1,2,3,
Wei Xian
4,
Huaiyong Shao
1,2,*,
Qiufang Shao
5 and
Jiaguo Qi
6
1
College of Earth Sciences, Chengdu University of Technology, Chengdu 610059, China
2
Key Laboratory of Earth Exploration and Information Technology, Ministry of Education, Chengdu 610059, China
3
College of Computer Science, Sichuan Normal University, Chengdu 610066, China
4
College of Resources and Environment, Chengdu University of Information Technology, Chengdu 610225, China
5
Teaching Steering Committee, Sichuan Tourism University, Chengdu 610100, China
6
Center for Global Change and Earth Observations, Michigan State University, East Lansing, MI 48824, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(5), 1404; https://doi.org/10.3390/rs15051404
Submission received: 26 December 2022 / Revised: 24 February 2023 / Accepted: 26 February 2023 / Published: 2 March 2023
(This article belongs to the Special Issue Recent Advances in Remote Sensing Modeling and Retrieving for Mountain Ecological Parameters)
Browse Figures
Versions Notes

Abstract

:
Rodents are a vital part of the natural succession chain of the alpine grassland ecosystem, and rodent activities have an important impact on alpine grassland ecology. Moderate rodent population activities positively improve soil permeability, promote nutrient cycling, and promote biodiversity. However, too much rodent population or excessive activity intensity will bring negative effects on the ecological environment. Therefore, it is of great significance to accurately grasp the rodent activity intensity (RAI) in alpine grassland to cope with the changes in rodent populations and maintain the stability of the alpine grassland ecosystem. The Zoige alpine grassland was used as the study area in this study. In addition, UAV was sent to sample the rodent activity area in the alpine grassland. With the aid of field survey data, the surface information of rodent activity in the experimental area was identified, and the RAI index in the sample plot was calculated. Then, based on Sentinel-2A satellite remote sensing multi-spectral data and spectral index, multiple linear regression (MLR), multi-layer perceptron neural networks (MPL neural nets), random forest (RF), and support vector regression (SVR) were used to construct four models for RAI and Sentinel-2 datasets. The accuracy of the four models was compared and analyzed. The results showed that the RF model had the highest prediction accuracy (R2 = 0.8263, RWI = 0.8210, LCCC = 0.8916, RMSE = 0.0840, MAE = 0.0549), followed by the SVR model, the MLP neural nets model, and the MLR model. Overall, the nonlinear relationship between rodent activity intensity and satellite remote sensing images is obvious. Machine learning with strong nonlinear fitting ability can better characterize the RAI in alpine grassland. The RF model, with the best accuracy, can quantitatively estimate RAI in the alpine grassland, providing theoretical and technical support for monitoring RAI and rodent control in the alpine grassland.

Graphical Abstract

1. Introduction

Grassland is an important ecological barrier as well as a material base for animal husbandry production [1]. At high latitudes or high altitudes, there are large areas of alpine grasslands [2,3], which are important ecological reserves and have significant ecological value for maintaining biodiversity and regional ecological balance [4,5,6]. Alpine grassland is also a vital water source conservation and supply area in the basin’s upper reaches, which has an important strategic position in the ecological protection and high-quality development of the watershed [7,8]. Since alpine grassland is susceptible to plateau climate, human activities, and animal disturbance [9], it is crucial to ensure the ecological regional security pattern and respond to climate change correctly [10,11].
Small mammals in the alpine grassland mainly include the Citellus dauricus, zokors, gerbils, pikas, and marmots (collectively referred to as “rodents” in this paper), which are important components of the natural succession chain of the alpine grassland ecosystem. Through digging, excreting, foraging, and other activities, rodents can significantly affect the soil formation process, nutrient content, and vegetation succession [12,13]. Moderate rodent population activities can improve soil permeability, promote nutrient cycling, and play an essential positive role in ensuring water conservation, improving the ecological landscape, and promoting biodiversity [14,15,16]. However, excessive rodent populations lead to a large number of high-quality herbage being eaten. More seriously, the dense and crisscrossed rodent holes change the soil surface structure and destroy vegetation [17,18,19]. It is easy to form secondary bare land, and the soil moisture and fertility are reduced. The extent of the problem will gradually expand and become large “bald spots” [20,21,22]. The activities of the rodent population directly affect soil properties and vegetation growth [23] and have an extremely important impact on the alpine grassland ecological environment [24].
Since the 1980s, alpine grassland in China has been seriously degraded, and its ecological functions have been destroyed. Many problems have been faced, such as decreased biodiversity, ecosystem service function, and environmental deterioration [25]. Large-scale rodent infestation has been considered a significant factor in the degradation of alpine grasslands in recent decades [23,26,27]. The rodent population is also reflected on the land surface. The greater the number of rodents, the greater the activity intensity and the more land surface traces will be produced. Therefore, it is of great significance to maintain the alpine grassland ecosystem and ensure the sustainable utilization of grassland resources by accurately grasping the rodent activity intensity (RAI) in alpine grasslands to cope with changes in rodent populations effectively. The RAI index was proposed for the first time in this study. It indicates the extent of the impact of rodent activity on the surface landscape in an area.
Currently, the standard method to investigate RAI in grassland is still a field survey based on the plot scale [28,29,30]. The disturbance of plateau rodents to soil and vegetation is the comprehensive result of various rodent activities. It is common to use the effective hole density per unit area to classify rodent disturbance intensity on plateau [31,32,33,34]. Chen believed that the total hole density of the plateau pika could reflect not only the plateau pika interference intensity but also the amount of excavation activity of the plateau pika [35]. Li and Zhang used the transect method to estimate the population density of plateau pika when the plateau pika activity peaked at the Haibei Alpine Meadow Ecosystem Positioning Station of the Chinese Academy of Sciences [36]. Niu estimated the number of pika holes in the sample plot using the blocked tunnel method [37] and calculated the density of pika holes in each sample plot [38]. Liu used the blocking and stealing holes method to continuously record the number of holes and the number of effective holes. After determining effective holes, the plateau pika was captured in the sample field until it was no longer captured. Finally, the number of captured plateau pika was used to calculate the hole coefficient of the plateau pika [39]. Yu and Zhang believed that the number of bare soil patches was directly related to the population density of plateau pika, so the percentage of bare soil area of each disturbed plot could be used as a representative of the plateau pika disturbance intensity [34]. The advantage of the field survey method is that it can obtain accurate data about RAI at the sample plot scale, which has obvious advantages for understanding and grasping RAI at the micro-scale [40,41]. However, the RAI data obtained from the sample plot survey are easily affected by the number of sample plots, survey area, and other factors. In this method, it is difficult to accurately obtain the spatio-temporal distribution data of RAI in the macro scale area, which is not conducive to the overall understanding of the spatio-temporal pattern of RAI.
Since 2013, UAVs have made a breakthrough in the field of rodent activity monitoring. Many scholars used UAVs to acquire images of prairie rodent damage and combined them with artificial intelligence, pattern recognition, and other methods to obtain the spatial distribution and damage degree of rodent damage in the grassland [42]. Ma and Sun took aerial photographs of the rodent infestation areas based on the UAV low-altitude remote sensing monitoring platform, and then calculated the coverage of hole clusters using the UAV low-altitude remote sensing images, classified the rodent infestation levels in the study area and analyzed the distribution of rodent infestation [43,44]. Dong carried out a study on the UAV remote sensing identification of rodent holes and rodent mounds information and achieved good accuracy [45]. Xuan built a low-altitude remote sensing platform using dynamic delta wings and digital cameras to obtain ultra-high resolution image data of grassland rodent infestation of about 1 cm. Additionally, the spatial distribution and damage degree of rodent infestation was obtained by using GIS spatial interpolation and statistical methods on the basis of manual interpretation [46]. With the development of UAV technology, field investigation method and low-altitude remote sensing technology are effectively combined. Aerial images with ultra-high spatial resolution can provide a finer spatial scale for directly mapping rodent hole distribution. Compared with the manual field survey method, the work efficiency and survey scope are greatly improved [47]. However, the continuous flight time of UAVs is limited, and it is not easy to meet the prediction of RAI in an extensive range and multiple periods.
In contrast, whether it is a manual field survey or UAV remote sensing survey, the point data of field monitoring can hardly reflect the spatial and temporal distribution of RAI in macro-scale areas comprehensively and accurately. Satellite remote sensing has the characteristics of macroscopic and multi-phase, which has advantages in estimating RAI in large-scale and multi-stage. The critical point is to study further the relationship between satellite remote sensing data and RAI. However, rodent activity information such as holes and mounds cannot be directly obtained from the images because the spatial resolution of satellite images is far less than UAV images. Fortunately, the surface landscape of alpine grassland is altered by rodent feeding and digging. Therefore, landscape changes caused by rodent activity can be used to estimate RAI [48].
There are mainly the following methods for estimating RAI based on satellite remote sensing. Firstly, construct the interpretation signs of rodent activity areas. For example, in a study by Li [49], Interpretation signs such as rodent infestation sites, grasslands, rodent wasteland, and bare land were constructed based on Landsat8 remote sensing images. Then, rodent-infested areas in the Altun Mountains grassland were identified and classified with the help of altitude and vegetation coverage. Secondly, build an evaluation model. He selected six indicators of elevation, slope, slope aspect, grassland type, soil type, and enhanced vegetation index (EVI) to construct a rodent damage estimation model. Different rat infestation areas and thresholds were extracted [50]. Thirdly, the changes in remote sensing indices were used to indirectly estimate the number of rodents. For example, Pianalto used the surface temperature extracted from the TM thermal infrared band to simulate the spatial pattern of desert rodent abundance at night [51]. Andreo used the number of rodents as the dependent variable and the vegetation index and moisture index as the independent variables to construct a fitting model based on Sentinel-2 and Landsat 8 satellite images [52]. In past research, indirect indicators such as vegetation index and comprehensive index were used to construct various models to estimate RAI, and various methods were also being tried and improved. The estimation of RAI by remote sensing was successfully reached. However, these indicators and methods are single and do not correlate satellite remote sensing data with field survey data and UAV survey data, resulting in low accuracy of estimation results.
The critical point of remote sensing estimation RAI is to find the relationship between RAI and satellite remote sensing data. Still, there may be complex nonlinear relationships between them, which linear regression models may not sufficiently reflect. In recent years, the extreme learning machine (ELM) [53] and multiple adaptive regression spline (MARS) model [54,55] were used to solve multiple nonlinear problems in the field of engineering technology, such as predicting the thermal conductivity of unsaturated soil [56] and evaluating the ultimate bearing capacity of geosynthetic-reinforced sand soil foundations [57]. Moreover, machine learning nonlinear regression algorithms, such as support vector machine [58], artificial neural network [59], and random forest [60], were applied to remote sensing regression fitting [61]. The experimental results of different methods are different. Therefore, finding the most suitable fitting model between RAI and satellite remote sensing data is the critical problem in estimating RAI in alpine grassland by satellite remote sensing.
This study was carried out on the Zoige alpine grassland. Satellite remote sensing data, UAV survey data, and field survey data were combined to construct the RAI estimation model. UAV remote sensing techniques and field surveys were used to extract rodent activity information from the sample sites. Meanwhile, multispectral datasets and remote sensing indicators from the Sentinel-2A satellite were used as indicators to estimate RAI. The plots used multiple linear regression, support vector machine, random forest, and MLP neural nets to research the relationship between the RAI and remote sensing indicators. The model with the highest accuracy was selected by verifying and comparing the prediction accuracy of the four models. The quantitative description of rodent activity can provide some theoretical and technical support for estimating rodent activity in alpine grassland. Study ideas and technical routes are shown in Figure 1.

2. Data and Method

2.1. Study Area

The area selected for this study is Zoige Alpine Grassland, which is located at the eastern edge of the Qinghai–Tibet Plateau, at the junction of Sichuan, Gansu, and Qinghai provinces, with a total area of about 10,326 km2 (Figure 2).
The Zoige alpine grassland is a typical alpine grassland ecological landscape area on the Qinghai–Tibet Plateau [62,63,64,65]. It is also an important water conservation and supply area in the upper reaches of the Yellow River [66,67]. In May 2022, the Zoige Grassland was approved as a national park, and the ecological benefits were raised to a high strategic position, which plays a vital role in guaranteeing and promoting the environmental protection and high-quality development of the upper Yellow River basin [7,8]. Zoige alpine grassland is a specific area that is comprehensively affected by plateau climate, human activities, animal disturbance, and other aspects. It has a direct indicator and early warning value for the grassland ecosystem of the Qinghai–Tibet Plateau [68,69]. It is vital to ensure the regional ecological security pattern and respond to climate change [70].
According to the actual statistics of the Sichuan Grassland Station, the average area of rodent damage in Sichuan grasslands in 2018 was 2.84 × 106 hm2, an increase of about 4.7% over 2017. Moreover, the severely damaged area is about 1.82 × 106 hm2, an increase of about 10% compared with 2017 [71]. Excessive rodent activity seriously affects the sustainable development of grassland animal husbandry. The sample plot selected for this study is located in Hongxing Town in the north of Zoige County, and the sample plot size is 500 m × 500 m. The primary rat species in this area are the zokor and the marmot, whose activity traces are typical.

2.2. Data Collection and Processing

2.2.1. UAV Data Acquisition and Processing

(1)
Flight plan of UAV
In the alpine grassland, the rodent population and the intensity of excavation were the highest in spring and autumn [72]. However, grassland vegetation gradually began to wither and yellow in autumn, which was not conducive to extracting vegetation indexes based on multispectral satellite data. According to the research of Dong [73] and Xiong [74], May 2021 was selected as the time for UAV remote sensing data collection. This time ensures that the surface rodent activity information obtained by UAV remote sensing represents the maximum RAI and allows the extraction of accurate vegetation indices using satellite remote sensing images in the same period.
A DJI Phantom 4 Pro Multi-rotor was used to take aerial photography of the sample site. The UAV is equipped with GPS/GLONASS dual-mode satellite positioning system, IMU, and compass dual redundant sensors, which can give images high-precision positioning information. The flight date was 12 May 2021; the flight altitude was 200 m, and the heading and side overlap rates were 80% and 60%, respectively.
(2)
Data Processing
The UAV image processing software Pix4Dmapper platform was used to convert the photos taken by the UAV into digital orthophotos [75]. Then the sample area is clipped out according to the size of 500 m × 500 m. The ground resolution of the UAV image is 0.05 m, which can clearly identify the surface traces of rodent activities. Combined with the information from the field investigation, the traces of rodent activities (including rodent holes and mounds) are interpreted by manual interpretation, which took 18 h. The interpretation results are shown in Figure 3.
According to the research of Pang [16], Yu [34], and Liu [39], the number of bare soil patches is directly related to the population density of plateau rodents, so the percentage of bare soil area in each disturbance plot can be used as a representative of the disturbance intensity of plateau rodents. In order to achieve a complete match between the UAV image and the Sentinel-2A image on the pixel scale, the interpretation results were gridded in this study, and the grid size was set to 10 × 10 m. Finally, the proportion of rodent activity trace areas in the grid was taken as the RAI index of the grid (Figure 3).

2.2.2. Collection and Processing of Sentinel-2A Data

(1)
Data source and description
In this study, Sentinel-2A satellite images were sourced from the ESA Copernicus Data Center (https://scihub.copernicus.eu/dhus/#/home, (accessed on 22 July 2021)). The image was taken on 9 May 2021, and the cloud cover was 0.2%. The imaging time of the satellite image is three days earlier than the UAV flight. During this period, there was no apparent natural change or human intervention in the sample plot. The field investigation results showed no signs of rodent activity, such as rodent holes and mounds recently added, and there was no significant growth in pastures. The authors believe that the temporal phases of the UAV image and satellite image used in this study are consistent and can be used to research the remote sensing estimation method of grassland RAI.
(2)
Data Processing
The images were radiometrically calibrated and atmospherically corrected in sen2cor software, then post-processed in SNAP software, and finally, the images of the plots were clipped in ENVI software. Sentinel-2A multispectral data has a total of 13 bands. Band 1 is used to monitor aerosols, Band 9 is used to monitor water vapor, and Band 10 is used to monitor ocean currents. The spatial resolution of the above three bands is low (only 60 m). The spatial resolution of the above three bands is low (only 60 m). These three bands should be excluded from this study and not be used as variables to construct the RAI estimation model in alpine grassland, so as to avoid interfering with model construction and reducing the model’s prediction accuracy.
Then, 14 derived indices were obtained through band calculation (Figure 4), including Enhanced Vegetation Index (EVI), Modified Soil Adjusted Vegetation Index (MSAVI), Normalized Difference Moisture Index (NDMI), Normalized Difference Soil Index (NDSI), Normalized Difference Vegetation Index (NDVI), Normalized Difference Vegetation Greenness Index (NDVGI), Normalized Moisture Index (NDWI), Ratio Vegetation Index (RVI), Soil Adjusted Vegetation Index (SAVI), Soil Color Index (SCI), Transformed Vegetation Index (TVI), Brightness Index (BI), Greenness Index (GI), and Wetness Index (WI).
There are many variables used for modeling, and the measurement standards of each variable are inconsistent. Therefore, all data were standardized before constructing models to improve the model’s sensitivity and ensure the accuracy of the estimation results.

2.3. Methodology

This study mainly consists of three stages: extracting the rodent activity area of the UAV image, constructing RAI estimation models, and comparing the model accuracy. RAI estimation was achieved by constructing an optimal inversion model between the RAI index and the spectral index [76]. This paper discussed four methods: multiple linear regression model, MLP neural nets model, random forest model, and support vector regression model.

2.3.1. Multiple Linear Regression

MLR models can describe the correlation between a dependent variable and multiple independent variables. The independent variables are added to the model one by one according to the correlation of the independent variables to the regression equation [77]. If the significance of the original variable is reduced after adding a new variable, the original variable is eliminated [78]. The addition or elimination of independent variables must pass the significance test to ensure that only the variables with large significance are included in the regression model [79,80]. In this study, 24 variables were added to the regression model according to the degree of correlation between the index and RAI. Variables with high significance were retained, and variables with minor significance were eliminated. The model equation for estimating the RAI was constructed as follows:
RAI = 0.168 + 0.145 × B2 − 0.363 × B3 + 0.166 × B4 + 0.002 × B5 − 0.012 × B6 − 0.054 × B7 − 0.167 × B8 + 0.002 × B8A + 0.371 × B11 − 0.070 × B12 + 0.49 × RVI + 0.388 × MSAVI + 0.355 × NDMI − 0.060 × NDGVI + 0.043 × EVI − 0.188 × TVI
where RAI is rodent activity intensity; B1~12 are band 1~12 of Sentinel-2A satellite image.

2.3.2. Multi-Layer Perception Neural Network

There may be a complex non-linear relationship between the 24 variables used for remote sensing inversion and the RAI values, which machine learning models can better reflect. Multi-layer perception neural networks (MLP neural nets) are artificial neural networks with a forward structure consisting of multiple node layers. Each layer is fully connected to the next layer, and the linearity is overcome by merging one or more hidden layers. It has a strong non-linear fitting ability and can map any complex non-linear relationship [81,82].
The MLP neural nets have three layers: the input layer, the hidden layer, and the output layer [83]. The input layer data were the spectral values and spectral indexes of the Sentinel-2A satellite image. In the hidden layer, the sigmoid function was selected as the activation function. The hidden layer was determined to be two layers, and the number of neurons in the first and second layers was 20 and 15, respectively. The output layer has only one layer, which is the RAI. The main parameters of the model in this study are as follows: the solver is “lbfgs”, the initial learning rate is 0.001, the L2 regular term is 0.01, and the number of training iterations is 500.
In training the neural network, the output value of the hidden layer and the predicted RAI index of the output layer were sequentially calculated by forward propagation. Then, the weights between the input layer and the hidden layer and between the hidden layer and the output layer were corrected by backpropagation. The above process was repeated until the maximum number of repetitions was reached. Optimizing network parameters was the process of constructing MLP neural nets.

2.3.3. Random Forest

Random forests (RF) is a machine learning model proposed by Breiman based on the classification and regression tree (CART) [84,85]. Random forest integrates several CARTs in parallel to construct a model with strong learning ability. When one CART makes an error, the other decision trees can correct it. The random forest algorithm has high efficiency for classification or regression with multidimensional features. It can process data with higher dimensions without dimensionality reduction and is simple to implement and fast to train [86].
The model randomly selects some samples from the training set. A set of samples is used to train a base-decision tree located at the tree’s root node. The information purity of the sample features is judged by the information gain rate or Gini index, and the best features are selected as the standard for splitting. Repeat the above steps to keep the base-decision tree growing until it meets the design. The random forest model is constructed by merging all the trained base-decision trees into a forest [87,88].
The performance of the RF model depends on the number of base-decision trees used. The more trees there are, the less easy the model is to overfit, but the computational effort will increase. In this study, the random search optimization method is used to find the optimal parameters. The optimal number of base-decision trees is 150, and the depth of a tree is 20. Max-features (the number of features to be used when splitting each node) is log2, min-samples-split (the minimum number of samples required to split internal nodes) is 8, min-samples-leaf (the minimum number of samples in each leaf) is 4, and the bootstrap (sampling method: put back the sample) is “true”.

2.3.4. Support Vector Regression

The support vector machine (SVM) is a machine learning model based on the statistical learning theory proposed by Cortes, which has excellent learning ability [89]. In dealing with pattern recognition problems, it can ensure that the training sample set and test sample set have small errors. It is widely used in environmental modeling, land use/cover classification, and the estimation of forest biomass. SVR is the regression algorithm model of SVM, whose basic idea is to find an optimal function that minimizes the “total deviation” of sample point distance.
SVR includes linear regression and nonlinear regression, and nonlinear regression is used in this study. The selection of the kernel function has a significant impact on the performance of the SVR model. In this study, the radial basis function (RBF) was selected as the kernel [90], and its prediction results depend on the distance to a specific point. The advantage of the RBF kernel function is that it is not constrained by the sample size when the data are mapped to a high-dimensional space and is resistant to perturbations in the data. Two critical parameters of the RBF kernel function are C and γ. C is the penalty coefficient, namely the tolerance for error. γ is the characteristic width of the kernel function and determines the scope of the kernel function [91]. Appropriate parameter settings will greatly improve the performance of the model. The parameter optimization algorithm obtained the optimal C and γ [92,93]. The optimal C = 54 and =1 were used to construct the SVR model in this study. The remaining main hyperparameters are as follows: the number of training iterations is 1696, shrinking is “true”, tol (the threshold for terminating iteration) is 0.001, random state is “none”, and epsilon (parameter e) is 0.1.

2.3.5. Model Assessment

To assess the four models’ accuracy, the sample data were divided into training sets and validation sets. A total of 70% of the sample data were randomly used for model construction, and 30% of the sample data were used for model accuracy validation [94]. Four statistical criteria were used to characterize the predictive performance of the model, including the coefficient of determination (R2), the root mean square error (RMSE), the mean absolute error (MAE), refined Wilmott index (RWI) [54], and Lin’s concordance correlation coefficient (LCCC) [95]. The larger the LCCC value and R2 value and the smaller the MAE value and RMSE value, the higher the accuracy of the estimated model.
R 2 = 1 − ∑ i = 1 n ( y i − z i ) 2 ∑ i = 1 n ( y i − y ¯ ) 2
R M S E = 1 n ∑ i = 1 n ( y i − z i ) 2
M A E = 1 n ∑ i = 1 n | y i − z i |
R W I = 1 − ∑ i = 1 n | y i − z i | 2 ∑ i = 1 n | y i − y ¯ |
L C C C = 2 r σ y σ z σ y 2 + σ z 2 + ( y _ − z _ ) 2
where n is the number of samples, yi is the RAI index measured by the UAV, zi is the RAI index predicted by the model, y _ is the mean of the measured values, z _ is the mean of the predicted values, σy2 is the variance of the measured values, σz2 the variance of the predicted values, and r is the Pearson correlation coefficient between the measured and predicted values [96].

3. Results and Analysis

3.1. Comparison of RAI Estimation Results

The MLR, MLP neural nets, RF, and SVR methods were used to construct the RAI estimation model. These four models were used to estimate the RAI of the plot area. Figure 5 shows the distribution of RAI in the plot.
According to RAI ≤ 0.1 (I), 0.1 < RAI ≤ 0.2 (II), 0.2 < RAI ≤ 0.3 (III), 0.3 < RAI ≤ 0.4 (IV), and RAI > 0.4 (V), the RAI of the sample plot was divided into five levels. The area of the RAI estimated by different methods is shown in Table 1. The RAI index of the sample plot interpreted and measured from the UAV image is the validation data. The sum of the areas of levels IV and V is 4.89 × 104 m2, accounting for 19.56% of the total sample plot area, and the areas of levels I and II are 17.66 × 104 m2, accounting for 70.64% of the total sample plot area.
It can be seen from Table 1 that there are certain differences in the RAI predicted by different methods. The prediction data of the MLR model have large errors with the validation data at each level. For predicting the area of level V, the accuracy of the three machine learning models is similar. Yet, they are about 30% smaller than the validation data. The area of level IV predicted by the machine learning model is very close to the verification data, and the difference between the prediction result of the RF model and the reality is only 0.11 × 104 m2. In the validation data, the area of level III is 2.45 × 104 m2. The prediction data of the machine learning model are larger than the validation data, and RF and SVR are 3.38 × 104 m2, which are the closest to the validation data. The prediction accuracy for level II is the lowest, and the error of MLR, MLP neural nets, and SVR models is more than 50%. RF is also the model with the highest accuracy for predicting the area of level Ⅰ.
The predicted value is always smaller than the verified value when RAI > 0.4 or RAI ≤ 0.1. The result is the opposite when 0.1 < RAI ≤ 0.4. The predicted value always tends to be the middle number. Comparing the prediction results of four models, it can be seen that the performance of MLP neural nets is obviously superior to the MLR model, but it is not the best method to estimate RAI. The RF is the model with the highest accuracy, and its prediction results are the closest to reality.
Twenty points were randomly selected in the sample plot, and the prediction results of the four models are shown in Figure 6. The results show that four models, MLR, MLP neural nets, RF, and SVR, can estimate RAI using satellite images in the study area. On the whole, the estimated results of the model are slightly smaller than the UAV measurement data, especially when the RAI is more significant than 0.35. The estimation results of the RF model are most similar to the UAV measurements.

3.2. Accuracy Assessment and Comparison

To illustrate the accuracy of estimating grassland RAI by various models at the study site, Figure 7 shows scatterplots of predicted versus verified RAI. It can be observed that the RF model has the highest saturation level.
The four models were used to predict the RAI of the plots, and the predictions were compared with the validation data to calculate the four statistical criteria. The results of the RAI estimation on the Sentinel-2A dataset using MLR, MLP neural nets, RF, and SVR models are shown in Table 2. It shows that the prediction performance of the nonlinear machine learning model is significantly better than the linear regression model. Comparing the three machine learning models, RF model has the highest goodness of fit and the best performance (R2 = 0.8263, RWI = 0.8210, LCCC = 0.8916, RMSE = 0.0840, MAE = 0.0549), followed by the SVR model (R2 = 0.6921, RWI = 0.7191, LCCC = 0.8195, RMSE = 0.1118, MAE = 0.0862), the MLP neural nets model (R2 = 0.6593, RWI = 0.6978, LCCC = 0.7899, RMSE = 0.1319, MAE = 0.0803). In contrast, the lowest goodness of fit was found for the MLR model (R2 = 0.3983, RWI = 0.6164, LCCC = 0.2695, RMSE = 0.1563, MAE = 0.1177).

4. Discussion

4.1. Advances and Innovations in This Study

In past research, the density of rodent holes [35], effective hole density [31], hole coefficient [39], bare soil spot density [34], and other indices were calculated to evaluate the population of grassland rodents or the impact of rodent activities on the grassland. However, these indices could not well reflect the impact of rodent activities on grassland. The RAI index was proposed for the first time in this study. It indicates the extent of the impact of rodent activity on the surface landscape in an area. This may provide a theoretical basis for future research.
In addition, traditional field surveys always take a long time, and it is difficult and error-prone to manually measure the area of rodent mounds [97]. The UAV measurement technology can map fine rodent holes and rodent mounds, so it can accurately estimate the RAI [47]. However, UAV endurance is short, which means it cannot support RAI estimation in large areas or for multiple periods [98]. Satellite imagery cannot be directly used to obtain RAI information, such as rodent holes and mounds, because its spatial resolution is much lower than that of UAV imagery. The main innovation of this study is to establish the relationship between satellite remote sensing and UAV remote sensing. This study is an exploration of estimating RAI using satellite remote sensing, which has rarely been reported in previous studies. The machine learning model combining UAV and satellite remote sensing proposed in this study is successful and has high fitting accuracy.

4.2. Select Input Variables for the Model

In existing research, NDVI, SAVI, NDWI, NDBI, and other spectral indexes are widely used [50,52,76]. However, the situation in a rodent activity area is much more complex than that of single vegetation coverage, so there is no conclusive conclusion on which factors have an influence on RAI, and the causal mechanism of various factors affecting RAI is unclear [48]. It is difficult to select the characteristic variables of the model. The SVR, RF, and MLP algorithms selected in this study are non-causal machine learning methods. There are no strict requirements for the causal mechanism of the input factors and independent variables, and the invalid factors have little impact on the regression results [99]. The MLR model can also gradually eliminate the variables with a small correlation. Therefore, as many input variables as possible are selected in this study and then processed by models with judgment and learning ability. This study selected 24 factors as input variables.
However, the MLP neural network model is susceptible to collinearity issues when there are a lot of feature variables. This is the reason why the accuracy of MLP neural nets is not high in this study. This is consistent with Zhang’s research results [100]. The advantage of the RF model is that it can handle high-dimensional data without repeatedly tuning parameters. Even if some feature variables are missing, the accuracy of the final result can be maintained. Its main advantages are strong generalization, low collinearity and outlier sensitivity, and difficulty in overfitting. This is consistent with the research results of Han, who pointed out that compared with traditional methods, random forest is not easily influenced by environmental noise and has high prediction accuracy [101].

4.3. Effectiveness of Machine Learning for Estimating RAI in Alpine Grassland

Because rodents are engaged in uninterrupted activities, it is difficult to obtain information directly about rodent activities [51]. It is still challenging to estimate grassland RAI using satellite remote sensing data in alpine grassland. In this study, four models were established to estimate RAI in alpine grassland. R2, RWI, LCCC, RMSE, and MAE were used to evaluate the estimation effect.
The prediction results of all four models are slightly smaller than the UAV validation data, especially when the RAI is more significant than 0.35. The reason is that the grass has some occlusions for the rodent hole and the rodent mound, but the resolution of the satellite image is so low that it is impossible to make a judgment close to that of the UAV image. The R2 and LCCC of the MLR model are 0.3983 and 0.2695, respectively, which not only shows that the linear regression model is unsuitable for grassland RAI remote sensing estimation but also indicates that the linear relationship between grassland RAI and spectral index is not apparent. This coincides with Melis’s research [102]. On the contrary, the three nonlinear regression machine learning models showed better performance (R2 = 0.6593–0.8263; LCCC = 0.7899–0.8916), indicating an evident nonlinear relationship between grassland RAI and Sentinel-2A satellite remote sensing data. This result is in agreement with the findings reported in Reference [103].

4.4. Shortcomings and Prospects

This study was carried out in a sample plot, and good results were obtained, which verified the effectiveness of using remote sensing technology to estimate alpine grassland RAI. It provides a high-efficiency and low-cost research idea for the next step to estimate the alpine grassland RAI on a large scale and in multiple stages. According to the research of Pei [104], there will be some new problems to be solved when small-scale research is promoted to large scale.
In the stage of processing the UAV image data, the traces of rodent activity are interpreted manually. Although the accuracy is high and the closest to the natural situation, the efficiency is very low. In order to realize the modeling of a larger area, the method of extracting rat activity traces from UAV images needs to be improved to improve efficiency while ensuring accuracy.
The sample plots selected for this study have flat terrain and few types of land cover, including only grassland, roads, and streams. The interference of the model is small, which ensures high prediction accuracy. However, it is unavoidable to encounter complex terrain or many land cover types when the study area is large, which may affect the performance of the model [99]. Therefore, in the next research plan, we will try to eliminate the interference of other land covers. In addition, the model is optimized by combining various algorithms to further improve the estimation accuracy and applied to estimate alpine grassland RAI on a large scale.

5. Conclusions

This study investigates using Sentinel-2A satellite remote sensing multispectral and UAV images to estimate the RAI of alpine grassland. In addition, four models, including MLR, MLP neural nets, RF, and SVR, were investigated and compared. Based on the findings of this study, the following conclusions are drawn.
(1)
Compared to MLR, MLP, and SVR, the RF model can provide the highest prediction accuracy for estimating the RAI of alpine grassland.
(2)
The nonlinear relationship between RAI and the satellite spectral index is apparent. Therefore, the machine learning model with nonlinear solid fitting ability is suitable for estimating the RAI of alpine grassland.
(3)
The alpine grassland RAI estimation model constructed by satellite remote sensing data can quantitatively describe the rodent activity in a certain area, which can provide theoretical and technical support for further monitoring of rodent control in alpine grassland.

Author Contributions

G.D.: methodology, data curation, software, validation, formal analysis, visualization, writing—original draft preparation. H.S.; methodology, investigation, resources, writing—review and editing. W.X.: investigation, methodology, formal analysis, writing—original draft preparation. Q.S.: supervision, resources, investigation. J.Q.: data curation, investigation, supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This study was funded by the National Natural Science Foundation of China (Grant No. 42271405) and the Science and Technology Department of Sichuan Province (Grant No. 2022NSFSC0231).

Data Availability Statement

The model developed in this study, as well as the data supporting the reported results, can be obtained by contacting the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wang, Q.; Yang, Y.; Liu, Y.Y.; Tong, L.J.; Zhang, Q.P.; Li, J.L. Assessing the impacts of drought on grassland net primary production at the global scale. Sci. Rep. 2019, 9, 14041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Ren, J.Z.; Li, X.L.; Hou, F.J. Research progress and trend on grassland agroecology. Chin. J. Appl. Ecol. 2002, 13, 1017–1021. [Google Scholar]
  3. Dong, S.K.; Shang, Z.H.; Gao, J.X.; Boone, R.B. Enhancing sustainability of grassland ecosystems through ecological restoration and grazing management in an era of climate change on Qinghai-Tibetan Plateau. Agric. Ecosyst. Environ. 2020, 287, 106684. [Google Scholar] [CrossRef]
  4. Liu, A.R.; Yang, T.; Xu, W.; Shangguan, Z.J.; Wang, J.Z.; Liu, H.Y.; Shi, Y.; Chu, H.Y.; He, J.S. Status, issues and prospects of belowground biodiversity on the Tibetan alpine grassland. Biodivers. Sci. 2018, 26, 972–987. [Google Scholar] [CrossRef]
  5. Xie, G.D.; Lu, C.X.; Xiao, Y.; Zheng, D. The economic evaluation of grassland ecosystem services in Qinghai-Tibet Plateau. Mt. Res. 2003, 21, 50–55. [Google Scholar]
  6. Yang, Q.; Liu, G.Y.; Giannetti, B.F.; Agostinho, F.; Almeida, C.M.V.B.; Casazza, M. Emergy-based ecosystem services valuation and classification management applied to China's grasslands. Ecosyst. Serv. 2020, 42, 101073. [Google Scholar] [CrossRef]
  7. Zhang, Y.P. Analysis on Spatial Distribution Patterns and Driving Forces of Degraded Alpine Grassland in the River Basin of the Yellow River Source Zone. Ph.D. Thesis, Qinghai University, Xining, China, 2022. [Google Scholar]
  8. Zhang, A.L. Response of Eco-Hydrology Evolution to Changing Environment in Grassland Watershed of Plateau Inland River. Master’s Thesis, Inner MongoliaAgricultural University, Hohhot, China, 2020. [Google Scholar]
  9. Zheng, Y.M.; Niu, Z.G.; Gong, P.; Li, M.N.; Hu, L.L.; Wang, L.; Yang, Y.X.; Gu, H.J.; Mu, J.R.; Dou, G.J.; et al. A method for alpine wetland delineation and features of border: Zoig Plateau, China. Chin. Geogr. Sci. 2017, 27, 784–799. [Google Scholar] [CrossRef] [Green Version]
  10. Xiang, S.; Guo, R.Q.; Wu, N.; Sun, S.C. Current status and future prospects of Zoige Marsh in Eastern Qinghai-Tibet Plateau. Ecol. Eng. 2009, 35, 553–562. [Google Scholar] [CrossRef]
  11. Sun, H.L.; Zheng, D.; Yao, T.D.; Zhang, Y.L. Protection and construction of the national ecological security shelter zone on Tibetan Plateau. Acta Geogr. Sin. 2012, 67, 3–12. [Google Scholar]
  12. Aho, K.; Huntly, N.; Moen, J.; Oksanen, T. Pikas (Ochotona princeps: Lagomorpha) as allogenic engineers in an alpine ecosystem. Oecologia. 1998, 114, 405–409. [Google Scholar] [CrossRef]
  13. Qin, Y.; Yi, S.; Ding, Y.; Zhang, W.; Qin, Y.; Chen, J.; Wang, Z. Effect of plateau pika disturbance and patchiness on ecosystem carbon emissions in alpine meadow in the northeastern part of Qinghai–Tibetan Plateau. Biogeosciences 2019, 16, 1097–1109. [Google Scholar]
  14. Wang, Q.; Yu, C.; Pang, X.P.; Jin, S.H.; Zhang, J.; Guo, Z.G. The disturbance and disturbance intensity of small and semi-fossorial herbivores alter the belowground bud density of graminoids in alpine meadows. Ecol. Eng. 2018, 113, 35–42. [Google Scholar] [CrossRef]
  15. Faiz, A.H.; Fakhar, I.A.; Faiz, L.Z. Burrowing Activity of Rodents Alter Soil Properties: A Case Study on the Short Tailed Mole Rat (Nesokia indica) in Pothwar Plateau, Punjab, Pakistan. Pak. J. Zool. 2018, 50, 719–724. [Google Scholar] [CrossRef]
  16. Pang, X.P.; Wang, Q.; Zhang, J.; Xu, H.P.; Zhang, W.N.; Wang, J.; Guo, Z.G. Responses of soil inorganic and organic carbon stocks of alpine meadows to the disturbance by plateau pikas. Eur. J. Soil Sci. 2020, 71, 706–715. [Google Scholar] [CrossRef]
  17. Retzer, V.; Reudenbach, C. Modelling the carrying capacity and coexistence of pika and livestock in the mountain steppe of the South Gobi, Mongolia. Ecol. Model. 2005, 189, 89–104. [Google Scholar] [CrossRef]
  18. Guo, Z.G.; Wang, Q.; Chen, H. Issues and suggestions for rodent control of the natural grassland in China. Pratacultural Sci. 2014, 31, 168–172. [Google Scholar]
  19. Castillo, J.A.; Epps, C.W.; Jeffress, M.R.; Ray, C.; Rodhouse, T.J.; Schwalm, D. Replicated landscape genetic and network analyses reveal wide variation in functional connectivity for American pikas. Ecol. Appl. 2016, 26, 1660–1676. [Google Scholar] [CrossRef]
  20. Wei, X.H. Investigation and control of rodent damage on fenced grassland in Songduo Town, Nyingchi, Tibet. Pratacultural Sci. 2003, 20, 48–49. [Google Scholar]
  21. Guo, W.J. The grassland rodent harmfulness and its control in Dangxiong county Tibet. Pratacultural Sci. 1999, 16, 48–50. [Google Scholar]
  22. Su, J.H.; Liu, R.T.; Ji, W.H.; Jiao, T.; Cai, Z.S.; Hua, L.M. Stages and characteristics of grassland rodent pests control and research in China. Pratacultural Sci. 2013, 30, 1116–1123. [Google Scholar]
  23. Sun, X.H.; Zhao, Y.; Li, Q. Holocene peatland development and vegetation changes in the Zoige Basin, eastern Tibetan Plateau. Sci. China-Earth Sci. 2017, 60, 1826–1837. [Google Scholar] [CrossRef]
  24. Liu, W.; Yang, K.; Xu, G.W.; Xu, H.K.; Xie, H.Q.; Zhong, X.S.; Liu, A.R. Disturbing effects of Plateau zokor(Myospalax baileyi) on grassland plant community in Ruoergai Plateau marshes. J. Sichuan Norm. Univ. (Nat. Sci.) 2020, 43, 84–88. [Google Scholar]
  25. Qiang, W.Q. Evaluation of Soil Quality and Ecological Environment Effect of Typical Grassland in Western China. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2020. [Google Scholar]
  26. Dong, Z.B.; Hu, G.Y.; Yan, C.Z.; Wang, W.L.; Lu, J.F. Aeolian desertification and its causes in the Zoige Plateau of China's Qinghai-Tibetan Plateau. Environ. Earth Sci. 2010, 59, 1731–1740. [Google Scholar] [CrossRef]
  27. Wang, D.L.; Li, X.C.; Pan, D.F.; De, K.J. The ecological significance and controlling of rodent outbreaks in the Qinghai-Tibetan Grasslands. J. Southwest Minzu Univ. (Nat. Sci. Ed.) 2016, 42, 237–245. [Google Scholar]
  28. Brady, M.J.; Slade, N.A. Diversity of a grassland rodent community at varying temporal scales: The role of ecologically dominant species. J. Mammal. 2001, 82, 974–983. [Google Scholar] [CrossRef]
  29. Feliciano, B.R.; Fernandez, F.a.S.; De Freitas, D.; Figueiredo, M.S.L. Population dynamics of small rodents in a grassland between fragments of Atlantic Forest in southeastern Brazil. Mamm. Biol. 2002, 67, 304–314. [Google Scholar] [CrossRef]
  30. Southgate, R.; Masters, P. Fluctuations of rodent populations in response to rainfall and fire in a central Australian hummock grassland dominated by Plectrachne schinzii. Wildl. Res. 1996, 23, 289–303. [Google Scholar] [CrossRef]
  31. Pang, X.P.; Guo, Z.G. Plateau pika disturbances alter plant productivity and soil nutrients in alpine meadows of the Qinghai-Tibetan Plateau, China. Rangel. J. 2017, 39, 133–144. [Google Scholar]
  32. Zhang, W.N.; Jin, S.H.; Yu, C.; Pang, X.P.; Wang, J.; Guo, Z.G. Influence of the density of burrow entrances of plateau pika on the concentration of soil nutrients in a Kobresia pygmaea meadow. Pratacultural Sci. 2018, 35, 1593–1601. [Google Scholar]
  33. Wangdwei, M.; Steele, B.; Harris, R.B. Demographic responses of plateau pikas to vegetation cover and land use in the Tibet Autonomous Region, China. J. Mammal. 2013, 94, 1077–1086. [Google Scholar]
  34. Yu, C.; Zhang, J.; Pang, X.P.; Wang, Q.; Zhou, Y.P.; Guo, Z.G. Soil disturbance and disturbance intensity: Response of soil nutrient concentrations of alpine meadow to plateau pika bioturbation in the Qinghai-Tibetan Plateau, China. Geoderma 2017, 307, 98–106. [Google Scholar] [CrossRef]
  35. Chen, J.; Wang, Z.Q.; Wang, Y.; Li, B.; Zhaxi, X.Z.; Luo, S.; Zhang, M.W. Methods for investigating the density of the plateau pika in Northern Tibetan Plateau. Plant Prot. 2008, 34, 114–117. [Google Scholar]
  36. Li, W.J.; Zhang, Y.M. Impacts of plateau pikas on soil organic matter and moisture content in alpine meadow. Acta Theriol. Sin. 2006, 26, 331–337. [Google Scholar]
  37. Sun, F.D.; Guo, Z.G.; Shang, Z.H.; Long, R.J. Effects of density of burrowing Plateau pikas (Ochotona curzoniae) on soil physical and chemical properties of alpine meadow soil. Acta Pedol. Sin. 2010, 47, 378–383. [Google Scholar]
  38. Niu, K.C.; Feng, F.; Xu, Q.; Zhang, S.T. Impoverished soil supports more plateau pika through lowered diversity of plant functional traits in Tibetan alpine meadows. Agric. Ecosyst. Environ. 2019, 285, 106621. [Google Scholar] [CrossRef]
  39. Liu, W.; Xu, Q.M.; Wang, X.; Zhao, J.Z.; Zhou, L. Influence of burrowing activity of plateau pikas (Ochotona curzoniae) on nitrogen in soils. Acta Theriol. Sin. 2010, 30, 35–44. [Google Scholar]
  40. Liu, R. Occurrence and control measures of rodents in Ordos grassland. Grassl. Prataculture 2011, 23, 10–13. [Google Scholar]
  41. Sun, F.D.; Gou, W.L.; Li, F.; Zhu, C.; Lu, H.; Chen, W.Y. Plateau pika population survey and its control threshold in the alpine meadow ecosystems of the Tibetan Plateau. Sichuan J. Zool. 2016, 35, 825–832. [Google Scholar]
  42. Zhou, X.L.; An, R.; Chen, Y.H.; Al, Z.T.; Huang, L.J. Identification of Rat Holes in the Typical Area of "Three-River Headwaters”Region By UAV Remote Sensing. J. Subtrop. Resour. Environ. 2018, 13, 85–92. [Google Scholar]
  43. Sun, D. Dynamic Monitoring and Change Analysis of Mouse-Hole by Eolagurus Luteus Based on Low Altitude Remote Sensing. Master’s Thesis, Xinjiang University, Ürümqi, China, 2019. [Google Scholar]
  44. Ma, T.; Zheng, J.H.; Wen, A.M.; Chen, M.; Liu, Z.J. Group coverage of burrow entrances and distribution characteristics of desert forest-dwelling Rhombomys opimus based on unmanned aerial vehicle (UAV) low-altitude remote sensing: A case study at the southern margin of the Gurbantunggut Desert in Xinjiang. Acta Ecol. Sin. 2018, 38, 953–963. [Google Scholar]
  45. Dong, G.; Di, W.; Cheng, W.X. Information extraction and comparison of zokor damage in Zoige grassland based on low-altitude remote sensing. J. Sichuan Norm. Univ. (Nat. Sci.) 2022, 45, 110–118. [Google Scholar]
  46. Xuan, J.W.; Zheng, J.H.; Ni, Y.F.; Mu, C. Research on remote sensing monitoring of grassland rodents based on dynamic delta wing platform. China Plant Prot. 2015, 35, 52–55. [Google Scholar]
  47. Hua, R.; Zhou, R.; Bao, D.E.H.; Dong, K.C.; Tang, Z.S.; Hua, L.M. A study of UAV remote sensing technology for classifying the level of plateau pika damage to alpine rangeland. Acta Prataculturae Sin. 2022, 31, 165–176. [Google Scholar]
  48. Angelopoulou, T.; Tziolas, N.; Balafoutis, A.; Zalidis, G.; Bochtis, D. Remote sensing techniques for soil organic carbon estimation: A review. Remote Sens. 2019, 11, 676. [Google Scholar] [CrossRef] [Green Version]
  49. Li, P.X.; Zheng, J.H.; Ni, Y.F.; Wu, J.G.; Wumaier, W.; Aihemaijiang, A.; Nasongcaoketu. Estimating area of grassland rodent damage gangeland and rat wastelands based on remote sensing in Altun Mountain, Xinjiang, China. Xinjiang Agric. Sci. 2016, 53, 1346–1355. [Google Scholar]
  50. He, Y.Q.; Huang, X.D.; Hou, X.M.; Feng, Q.S.; Wang, W.; Guo, Z.G.; Liang, T.G. Monitoring grassland rodents with 3S technologies. Acta Prataculturae Sin. 2013, 22, 33–40. [Google Scholar]
  51. Pianalto, F.S.; Yool, S.R. Sonoran Desert rodent abundance response to surface temperature derived from remote sensing. J. Arid Environ. 2017, 141, 76–85. [Google Scholar] [CrossRef]
  52. Andreo, V.; Belgiu, M.; Brito Hoyos, D.; Osei, F.; Provensal, C.; Stein, A. Rodents and satellites: Predicting mice abundance and distribution with Sentinel-2 data. Ecol. Inform. 2019, 51, 157–167. [Google Scholar] [CrossRef]
  53. Bardhan, A.; Samui, P.; Ghosh, K.; Gandomi, A.H.; Bhattacharyya, S. ELM-based adaptive neuro swarm intelligence techniques for predicting the California bearing ratio of soils in soaked conditions. Appl. Soft Comput. 2021, 110, 107595. [Google Scholar] [CrossRef]
  54. Raja, M.N.A.; Shukla, S.K. Predicting the settlement of geosynthetic-reinforced soil foundations using evolutionary artificial intelligence technique. Geotext. Geomembr. 2021, 49, 1280–1293. [Google Scholar] [CrossRef]
  55. Raja, M.N.A.; Shukla, S.K. Multivariate adaptive regression splines model for reinforced soil foundations. Geosynth. Int. 2021, 28, 368–390. [Google Scholar] [CrossRef]
  56. Kardani, N.; Bardhan, A.; Samui, P.; Nazem, M.; Zhou, A.; Armaghani, D.J. A novel technique based on the improved firefly algorithm coupled with extreme learning machine (ELM-IFF) for predicting the thermal conductivity of soil. Eng. Comput. 2022, 38, 3321–3340. [Google Scholar] [CrossRef]
  57. Raja, M.N.A.; Shukla, S.K. An extreme learning machine model for geosynthetic-reinforced sandy soil foundations. Proc. Inst. Civ. Eng.-Geotech. Eng. 2022, 175, 383–403. [Google Scholar] [CrossRef]
  58. Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. Isprs J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
  59. Yuan, H.H.; Yang, G.J.; Li, C.C.; Wang, Y.J.; Liu, J.G.; Yu, H.Y.; Feng, H.K.; Xu, B.; Zhao, X.Q.; Yang, X.D. Retrieving soybean leaf area index from unmanned aerial vehicle hyperspectral remote sensing: Analysis of RF, ANN, and SVM regression models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef] [Green Version]
  60. Zhu, X.L.; Liu, D.S. Improving forest aboveground biomass estimation using seasonal Landsat NDVI time-series. Isprs J. Photogramm. Remote Sens. 2015, 102, 222–231. [Google Scholar] [CrossRef]
  61. Sha, Z.Y.; Wang, Y.W.; Bai, Y.F.; Zhao, Y.J.; Jin, H.; Na, Y.; Meng, X.L. Comparison of leaf area index inversion for grassland vegetation through remotely sensed spectra by unmanned aerial vehicle and field-based spectroradiometer. J. Plant Ecol. 2019, 12, 395–408. [Google Scholar] [CrossRef] [Green Version]
  62. Li, P.; Zhu, Q.; Peng, C.H.; Zhang, J.; Wang, M.; Zhang, J.J.; Ding, J.H.; Zhou, X.L. Change in autumn vegetation phenology and the climate controls from 1982 to 2012 on the Qinghai-Tibet Plateau. Front. Plant Sci. 2020, 10, 1677. [Google Scholar] [CrossRef] [Green Version]
  63. Bai, J.P. Research on Ecological Recovery Procedure and Ecosystem Service Function of Desertifi Cation Grassland Governance Area in Zoige County. Master’s Thesis, Sichuan Agricultural University, Chengdu, China, 2013. [Google Scholar]
  64. Luan, J.W.; Cui, L.J.; Xiang, C.H.; Wu, J.H.; Song, H.T.; Ma, Q.F. Soil carbon stocks and quality across intact and degraded alpine wetlands in Zoige, east Qinghai-Tibet Plateau. Wetl. Ecol. Manag. 2014, 22, 427–438. [Google Scholar] [CrossRef]
  65. Hu, G.Y.; Yu, L.P.; Dong, Z.B.; Lu, J.F.; Li, J.Y.; Wang, Y.X.; Lai, Z.L. Holocene aeolian activity in the Zoige Basin, northeastern Tibetan Plateau, China. Catena 2018, 160, 321–328. [Google Scholar] [CrossRef]
  66. Wu, C.Y.; Chen, W.; Cao, C.X.; Tian, R.; Liu, D.; Bao, D.M. Diagnosis of wetland ecosystem health in the Zoige Wetland, Sichuan of China. Wetlands 2018, 38, 469–484. [Google Scholar] [CrossRef]
  67. Shen, G.; Yang, X.C.; Jin, Y.X.; Xu, B.; Zhou, Q.B. Remote sensing and evaluation of the wetland ecological degradation process of the Zoige Plateau Wetland in China. Ecol. Indic. 2019, 104, 48–58. [Google Scholar] [CrossRef]
  68. He, L. Study on the Remote Sensing Retrieval of Aboveground Biomass in the ZoigegrassLand Based on PROSAIL and GPR Models. Doctor Thesis, Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu, China, 2020. [Google Scholar]
  69. He, L.; Li, A.N.; Yin, G.F.; Nan, X.; Bian, J.H. Retrieval of Grassland Aboveground Biomass through Inversion of the PROSAIL Model with MODIS Imagery. Remote Sens. 2019, 11, 1597. [Google Scholar] [CrossRef] [Green Version]
  70. Bruun, T.B.; Elberling, B.; De Neergaard, A.; Magid, J. Organic carbon dynamics in different soil types after conversion of forest to agri-culture. Land Degrad. Dev. 2015, 26, 272–283. [Google Scholar] [CrossRef]
  71. Tu, M.G.; Lu, H.; Shang, M. Monitoring grassland desertification in Zoige County using Landsat and UAV image. Pol. J. Environ. Stud. 2021, 30, 5789–5799. [Google Scholar] [CrossRef]
  72. Yan, Z.L.; Zhou, L.; Sun, Y.; Liu, W.; Zhou, H.K. A research about the population dynamic model of Ochotona curzoniae in alpine meadows of source region of Yangtze and Y ellow River. J. Grassl. Forage Sci. 2005, 114, 17–19. [Google Scholar]
  73. Dong, G. Comparison on Methods of Extracting Rodent Damage Information in Zoige Grassland Based on Low-Altitude Remote Sensing. Master’s Thesis, Sichuan Normal University, Chengdu, China, 2019. [Google Scholar]
  74. Xiong, R.D. Study on the Estimation of the Damage Degree of Rats in Zoige Alpine Grassland Based on Low-Altitude Remote Sensing. Master’s Thesis, Sichuan Normal University, Chengdu, China, 2020. [Google Scholar]
  75. Yang, L.L. Application of Aerial Photogrammetry Based on Light and Small Unmanned Aerial Vehicle in Geometric Information Survey of High and Steep Slope. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2017. [Google Scholar]
  76. Porcasi, X.; Calderon, G.; Lamfri, M.; Gardenal, N.; Polop, J.; Sabattini, M.; Scavuzzo, C.M. The use of satellite data in modeling population dynamics and prevalence of infection in the rodent reservoir of Junin virus. Ecol. Model. 2005, 185, 437–449. [Google Scholar] [CrossRef]
  77. Liu, H.X.; Zhang, A.B.; Liu, C.; Zhao, Y.L.; Zhao, A.Z.; Wang, D.L. Analysis of the time-lag effects of climate factors on grassland productivity in Inner Mongolia. Glob. Ecol. Conserv. 2021, 30, e01751. [Google Scholar] [CrossRef]
  78. Eberly, L.E. Multiple linear regression. Methods Mol. Biol. 2007, 404, 165–187. [Google Scholar]
  79. Slinker, B.K.; Glantz, S.A. Multiple linear regression is a useful alternative to traditional analyses of variance. Am. J. Physiol. 1988, 255, R353–R367. [Google Scholar] [CrossRef]
  80. Pandis, N. Multiple linear regression analysis. Am. J. Orthod. Dentofac. Orthop. 2016, 149, 581. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  81. Delogu, R.; Fanni, A.; Montisci, A. Geometrical synthesis of MLP neural networks. Neurocomputing 2008, 71, 919–930. [Google Scholar] [CrossRef]
  82. Zare, M.; Pourghasemi, H.R.; Vafakhah, M.; Pradhan, B. Landslide susceptibility mapping at Vaz Watershed (Iran) using an artificial neural network model: A comparison between multilayer perceptron (MLP) and radial basic function (RBF) algorithms. Arab. J. Geosci. 2013, 6, 2873–2888. [Google Scholar] [CrossRef]
  83. Pham, B.T.; Shirzadi, A.; Bui, D.T.; Prakash, I.; Dholakia, M.B. A hybrid machine learning ensemble approach based on a Radial Basis Function neural network and Rotation Forest for landslide susceptibility modeling: A case study in the Himalayan area, India. Int. J. Sediment Res. 2018, 33, 157–170. [Google Scholar] [CrossRef]
  84. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  85. Heung, B.; Bulmer, C.E.; Schmidt, M.G. Predictive soil parent material mapping at a regional-scale: A Random Forest approach. Geoderma 2014, 214, 141–154. [Google Scholar] [CrossRef]
  86. Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. Isprs J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
  87. Probst, P.; Wright, M.N.; Boulesteix, A.-L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev.-Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef] [Green Version]
  88. Speiser, J.L.; Miller, M.E.; Tooze, J.; Ip, E. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst. Appl. 2019, 134, 93–101. [Google Scholar] [CrossRef]
  89. Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
  90. Meng, B.P.; Gao, J.L.; Liang, T.G.; Cui, X.; Ge, J.; Yin, J.P.; Feng, Q.S.; Xie, H.J. Modeling of Alpine Grassland Cover Based on Unmanned Aerial Vehicle Technology and Multi-Factor Methods: A Case Study in the East of Tibetan Plateau, China. Remote Sens. 2018, 10, 320. [Google Scholar] [CrossRef] [Green Version]
  91. Gu, T.L.; Chen, H.Y.; Chang, L.; Li, L. Intrusion detection system based on improved abc algorithm with tabu search. Ieej Trans. Electr. Electron. Eng. 2019, 14, 1652–1660. [Google Scholar] [CrossRef]
  92. Tien Bui, D.; Tuan, T.A.; Hoang, N.-D.; Thanh, N.Q.; Nguyen, D.B.; Liem, N.V.; Pradhan, B. Spatial prediction of rainfall-induced landslides for the Lao Cai area (Vietnam) using a hybrid intelligent approach of least squares support vector machines inference model and artificial bee colony optimization. Landslides. 2017, 14, 447–458. [Google Scholar] [CrossRef]
  93. Tien Bui, D.; Le, K.-T.T.; Nguyen, V.C.; Le, H.D.; Revhaug, I. Tropical forest fire susceptibility mapping at the Cat Ba National Park area, Hai Phong City, Vietnam, using GIS-Based kernel logistic regression. Remote Sens. 2016, 8, 347. [Google Scholar] [CrossRef] [Green Version]
  94. Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.D.; Bui, D.T. Improving Accuracy Estimation of Forest Aboveground Biomass Based on Incorporation of ALOS-2 PALSAR-2 and Sentinel-2A Imagery and Machine Learning: A Case Study of the Hyrcanian Forest Area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef] [Green Version]
  95. Lin, L.I. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef] [PubMed]
  96. Wang, B.; Waters, C.; Orgill, S.; Cowie, A.; Clark, A.; Liu, D.; Simpson, M.; Mcgowen, I.; Sides, T. Estimating soil organic carbon stocks using different modelling techniques in the semi-arid rangelands of eastern Australia. Ecol. Indic. 2018, 88, 425–438. [Google Scholar] [CrossRef]
  97. Ling, H.X. Study on occurrence of Aletai Grassland rodent in Aletai Xinjiang. Grass-Feed. Livest. 2014, 88, 49–51. [Google Scholar]
  98. Liu, X.Y. Identification and Hazard Asessmennt of Ancient Landslides Based on Multi-Source Remote Sensing Technology. Ph.D. Thesis, Chinese Academy of Geological Sciences, Beijing, China, 2020. [Google Scholar]
  99. Shi, H.Y.; Pan, Q.; Luo, G.P.; Hellwich, O.; Chen, C.B.; Van De Voorde, T.; Kurban, A.; De Maeyer, P.; Wu, S.X. Analysis of the Impacts of Environmental Factors on Rat Hole Density in the Northern Slope of the Tienshan Mountains with Satellite Remote Sensing Data. Remote Sens. 2021, 13, 4709. [Google Scholar] [CrossRef]
  100. Zhang, F.; Zhang, Y.Y.; Chen, J.X.; Zhai, X.Y.; Hu, Q.F. Performance of multiple machine learning model simulation of process characteristic indicators of different flood types. Prog. Geogr. 2022, 41, 1239–1250. [Google Scholar] [CrossRef]
  101. Han, T.; Jiang, D.X.; Zhao, Q.; Wang, L.; Yin, K. Comparison of random forest, artificial neural networks and support vector machine for intelligent diagnosis of rotating machinery. Trans. Inst. Meas. Control. 2018, 40, 2681–2693. [Google Scholar] [CrossRef]
  102. Melis, C.; Szafranska, P.A.; Jedrzejewska, B.; Barton, K. Biogeographical variation in the population density of wild boar (Sus scrofa) in western Eurasia. J. Biogeogr. 2006, 33, 803–811. [Google Scholar] [CrossRef]
  103. Baltensperger, A.P.; Huettmann, F. Predictive spatial niche and biodiversity hotspot models for small mammal communities in Alaska: Applying machine-learning to conservation planning. Landsc. Ecol. 2015, 30, 681–697. [Google Scholar] [CrossRef]
  104. Pei, Y.J. Accuracy Evaluation of Monitoring Rocky Desertification in Southeastern Yunnan Using Multi-Scale Remote Sensing. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2014. [Google Scholar]
Remotesensing 15 01404 g001 550
Figure 1. Study ideas and technical routes.
Figure 1. Study ideas and technical routes.
Remotesensing 15 01404 g001
Remotesensing 15 01404 g002 550
Figure 2. Location of the study area.
Figure 2. Location of the study area.
Remotesensing 15 01404 g002
Remotesensing 15 01404 g003 550
Figure 3. Interpretation results of rodent activity traces were gridded.
Figure 3. Interpretation results of rodent activity traces were gridded.
Remotesensing 15 01404 g003
Remotesensing 15 01404 g004 550
Figure 4. Fourteen spectral indices were calculated by band operation.
Figure 4. Fourteen spectral indices were calculated by band operation.
Remotesensing 15 01404 g004
Remotesensing 15 01404 g005 550
Figure 5. Calculate RAI distribution of the sample plot using: (a) UAV image; (b) the MLR model; (c) the MLP neural nets model; (d) the RF model; and (e) the SVR model.
Figure 5. Calculate RAI distribution of the sample plot using: (a) UAV image; (b) the MLR model; (c) the MLP neural nets model; (d) the RF model; and (e) the SVR model.
Remotesensing 15 01404 g005
Remotesensing 15 01404 g006 550
Figure 6. Comparison of the predicted RAI and the measured RAI values.
Figure 6. Comparison of the predicted RAI and the measured RAI values.
Remotesensing 15 01404 g006
Remotesensing 15 01404 g007 550
Figure 7. Comparison between the measured and predicted RAI using: (a) the MLR model; (b) the MLP neural nets model; (c) the RF model; and (d) the SVR model.
Figure 7. Comparison between the measured and predicted RAI using: (a) the MLR model; (b) the MLP neural nets model; (c) the RF model; and (d) the SVR model.
Remotesensing 15 01404 g007
Table
Table 1. The area of different RAI levels was calculated and compared.
Table 1. The area of different RAI levels was calculated and compared.
RAI Level (I)
RAI ≤ 0.1 		(II)
0.1 < RAI ≤ 0.2 		(III)
0.2 < RAI ≤ 0.3 		(IV)
0.3 < RAI ≤ 0.4 		(V)
RAI > 0.4
Model
Validation13.124.542.451.623.27
MLR8.547.225.532.711.00
MLP Neural Nets9.447.963.511.822.27
RF11.256.183.381.732.46
SVR9.198.013.381.942.48
The unit of data in the table is 104 m2.
Table
Table 2. Validation results of the RAI model.
Table 2. Validation results of the RAI model.
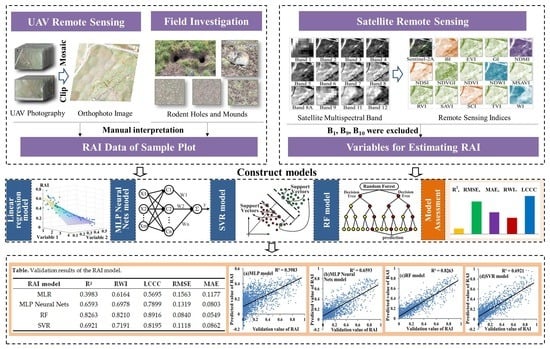
RAI Model R2 RWI LCCC RMSE MAE
MLR0.39830.61640.56950.15630.1177
MLP Neural Nets0.65930.69780.78990.13190.0803
RF0.82630.82100.89160.08400.0549
SVR0.69210.71910.81950.11180.0862
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Dong, G.; Xian, W.; Shao, H.; Shao, Q.; Qi, J. Performance of Multiple Models for Estimating Rodent Activity Intensity in Alpine Grassland Using Remote Sensing. Remote Sens. 2023, 15, 1404. https://doi.org/10.3390/rs15051404

AMA Style

Dong G, Xian W, Shao H, Shao Q, Qi J. Performance of Multiple Models for Estimating Rodent Activity Intensity in Alpine Grassland Using Remote Sensing. Remote Sensing. 2023; 15(5):1404. https://doi.org/10.3390/rs15051404

Chicago/Turabian Style

Dong, Guang, Wei Xian, Huaiyong Shao, Qiufang Shao, and Jiaguo Qi. 2023. "Performance of Multiple Models for Estimating Rodent Activity Intensity in Alpine Grassland Using Remote Sensing" Remote Sensing 15, no. 5: 1404. https://doi.org/10.3390/rs15051404

APA Style

Dong, G., Xian, W., Shao, H., Shao, Q., & Qi, J. (2023). Performance of Multiple Models for Estimating Rodent Activity Intensity in Alpine Grassland Using Remote Sensing. Remote Sensing, 15(5), 1404. https://doi.org/10.3390/rs15051404

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop