Three-Dimensional Dual-Mesh Inversions for Sparse Surface-to-Borehole TEM Data
Abstract
:1. Introduction
2. Methods
2.1. Regularized Inversion
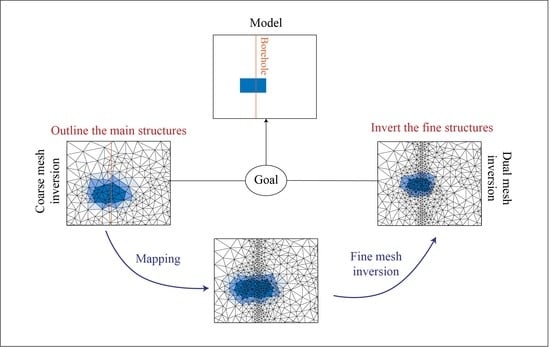
2.2. Dual-Mesh Inversion Strategy
3. Numerical Experiments
3.1. Flat Model Inversion
3.2. Topographic Model Inversion
3.3. Field Data Inversion
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Li, J. Inversion Algorithms for Electromagnetic Problems in Well: Numerical Examples in Reservoir Target Detection. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2015. [Google Scholar]
- Augustin, A.M.; Kennedy, W.D.; Morrison, H.F.; Lee, K.H. A theoretical study of surface-to-borehole electromagnetic logging in cased holes. Geophysics 1989, 54, 90–99. [Google Scholar] [CrossRef]
- Malmqvist, L.; Pantze, R. Directional EM-measurements in boreholes. Geoexploration 1981, 19, 149–150. [Google Scholar] [CrossRef]
- Lane, R.J.L. The downhole EM response of an intersected massive sulphide deposit, South Australia. Explor. Geophys. 1987, 18, 313–318. [Google Scholar] [CrossRef]
- Silic, J.; Eadie, E.T. DHEM: The Que-Hellyer Volcanics experience. Explor. Geophys. 1989, 20, 65–69. [Google Scholar] [CrossRef]
- Vella, L. Petrophysical characteristics of BIF-hosted gold deposits and the application of downhole EM to their exploration, with examples from Hill 50 gold mine, Mt Magnet, Western Australia. Explor. Geophys. 1995, 26, 106–115. [Google Scholar] [CrossRef]
- Paggi, J.; Macklin, D. Discovery of the Eureka volcanogenic massive sulphide lens using downhole electromagnetics. Explor. Geophys. 2016, 47, 248–257. [Google Scholar] [CrossRef]
- Wei, B.; Zhang, G. Imaging method in surface-to-borehole electromagnetic system. Shi You Da Xue Xue Bao 1999, 23, 24–29. [Google Scholar]
- Zhang, Z.; Xiao, J. Inversions of surface and borehole data from a large-loop transient electromagnetic system over a 1-D earth. Geophysics 2001, 66, 1090–1096. [Google Scholar] [CrossRef]
- Chen, W.; Han, S.; Khan, M.Y.; Chen, W.; He, Y.; Zhang, L.; Hou, D.; Xue, G. A Surface-to-Borehole TEM System Based on Grounded-wire Sources: Synthetic Modeling and Data Inversion. Pure Appl. Geophys. 2020, 177, 4207–4216. [Google Scholar] [CrossRef]
- Chen, W.; Han, S.; Xue, G. Analysis on the full-component response and detectability of electric source surface-to-borehole TEM method. Acta Geophys. Sin. 2019, 62, 1969–1980. [Google Scholar] [CrossRef]
- Lajoie, J.J.; West, G.F. The electromagnetic response of a conductive inhomogeneity in a layered earth. Geophysics 1976, 41, 1133–1156. [Google Scholar] [CrossRef]
- West, R.C.; Ward, S.H. The borehole transient electromagnetic response of a three-dimensional fracture zone in a conductive half-space. Geophysics 1988, 53, 1469–1478. [Google Scholar] [CrossRef]
- Eaton, P.A.; Hohmann, G.W. The influence of a conductive host on two-dimensional borehole transient electromagnetic responses. Geophysics 1984, 49, 861–869. [Google Scholar] [CrossRef] [Green Version]
- Christoph, S.; Ralph-Uwe, B.; Klaus, S. Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics—A marine CSEM example. Geophys. J. Int. 2011, 187, 63–74. [Google Scholar]
- Yin, C.; Qi, Y.; Liu, Y.; Cai, J. 3D time-domain airborne EM forward modeling with topography. J. Appl. Geophys. 2016, 134, 11–22. [Google Scholar] [CrossRef]
- Gu, G.; Li, T. Three-dimensional magnetotelluric inversion with surface topography based on the vector finite element method. Acta Geophys. Sin. 2020, 63, 2449–2465. [Google Scholar] [CrossRef]
- Kordy, M.; Wannamaker, P.; Maris, V.; Cherkaev, E.; Hill, G. 3-D magnetotelluric inversion including topography using deformed hexahedral edge finite elements and direct solvers parallelized on SMP computers; Part I, Forward problem and parameter Jacobians. Geophys. J. Int. 2016, 204, 74–93. [Google Scholar] [CrossRef]
- Um, E.S. Three-Dimensional Finite-Element Time-Domain Modeling of the Marine Controlled-Source Electromagnetic Method. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2011. [Google Scholar]
- Oldenburg, D.W.; Haber, E.; Shekhtman, R. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics 2013, 78, E47–E57. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Lu, X.; Colin, G.F.; Hu, X. A finite-element time-domain forward solver for electromagnetic methods with complex-shaped loop sources. Geophysics 2018, 83, E117–E132. [Google Scholar] [CrossRef]
- Yang, D.; Fournier, D.; Kang, S.; Oldenburg, D.W. Deep mineral exploration using multi-scale electromagnetic geophysics; the Lalor massive sulphide deposit case study. Can. J. Earth Sci. 2019, 56, 544–555. [Google Scholar] [CrossRef]
- Yang, D.; Oldenburg, D.W. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit. Geophysics 2012, 77, B23–B34. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Yin, C.; Liu, Y.; Su, Y.; Ren, X.; Hui, Z.; Zhang, B.; Xiong, B. Three-dimensional forward modeling for the SBTEM method using an unstructured finite-element method. Appl. Geophys. 2021, 18, 101–116. [Google Scholar] [CrossRef]
- Hui, Z.; Yin, C.; Liu, Y.; Zhang, B.; Ren, X.; Wang, C. 3D inversions of time-domain marine EM data based on unstructured finite-element method. Acta Geophys. Sin. 2020, 63, 3167–3179. [Google Scholar] [CrossRef]
- Qi, Y.; Zhi, Q.; Li, X.; Jing, X.; Qi, Z.; Sun, N.; Zhou, J.; Liu, W. Three-dimensional ground TEM inversion over a topographic earth considering ramp time. Acta Geophys. Sin. 2021, 64, 2566–2577. [Google Scholar] [CrossRef]
- Key, K. MARE2DEM: A 2-D inversion code for controlled-source electromagnetic and magnetotelluric data. Geophys. J. Int. 2016, 207, 571–588. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Yin, C.; Qiu, C.; Hui, Z.; Zhang, B.; Ren, X.; Weng, A. 3-D inversion of transient EM data with topography using unstructured tetrahedral grids. Geophys. J. Int. 2019, 217, 301–318. [Google Scholar] [CrossRef]
- Si, H. TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator. ACM Trans. Math. Softw. 2015, 41, 1–36. [Google Scholar] [CrossRef]
- Jin, J.-M. The Finite Element Method in Electromagnetics, 2nd ed.; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Um, E.S.; Harris, J.M.; Alumbaugh, D.L. 3D time-domain simulation of electromagnetic diffusion phenomena; a finite-element electric-field approach. Geophysics 2010, 75, F115–F126. [Google Scholar] [CrossRef]
- Amestoy, P.R.; Duff, I.S.; L’Excellent, J.-Y.; Koster, J. A Fully Asynchronous Multifrontal Solver Using Distributed Dynamic Scheduling. SIAM J. Matrix Anal. Appl. 2001, 23, 15–27. [Google Scholar] [CrossRef] [Green Version]
















| No. | Borehole Depth (m) | Core Properties | ρ0 (Ω·m) |
|---|---|---|---|
| wx-1 | 596.74–596.84 | porphyritic quartz monzodiorite | 7178 |
| wx-2 | 764.84–764.94 | copper-bearing hematite magnetite ore | 8.7 |
| wx-3 | 802.43–802.54 | marble rock | 1125 |
| wx-4 | 879.75–879.85 | marble rock | 374 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liu, Y.; Yin, C.; Su, Y.; Ren, X.; Zhang, B. Three-Dimensional Dual-Mesh Inversions for Sparse Surface-to-Borehole TEM Data. Remote Sens. 2023, 15, 1845. https://doi.org/10.3390/rs15071845
Wang L, Liu Y, Yin C, Su Y, Ren X, Zhang B. Three-Dimensional Dual-Mesh Inversions for Sparse Surface-to-Borehole TEM Data. Remote Sensing. 2023; 15(7):1845. https://doi.org/10.3390/rs15071845
Chicago/Turabian StyleWang, Luyuan, Yunhe Liu, Changchun Yin, Yang Su, Xiuyan Ren, and Bo Zhang. 2023. "Three-Dimensional Dual-Mesh Inversions for Sparse Surface-to-Borehole TEM Data" Remote Sensing 15, no. 7: 1845. https://doi.org/10.3390/rs15071845
APA StyleWang, L., Liu, Y., Yin, C., Su, Y., Ren, X., & Zhang, B. (2023). Three-Dimensional Dual-Mesh Inversions for Sparse Surface-to-Borehole TEM Data. Remote Sensing, 15(7), 1845. https://doi.org/10.3390/rs15071845