Impacts of Water and Stress Transfers from Ground Surface on the Shallow Earthquake of 11 November 2019 at Le Teil (France)

Abstract

The 4.9 Mw earthquake of 11 November 2019 at Le Teil (France) occurred at a very shallow depth (about 1 km), inducing the surface rupture of La Rouvière fault. The question was raised shortly after about the potential impact of a nearby surface quarry. Thanks to satellite differential interferometry, here, we revealed the existence of a secondary surface rupture of the quasi-parallel Bayne Rocherenard fault. A newly processed seismic cross-section allowed us to shape the three-dimensional geometry of the local three-fault system. Assuming that the earthquake was triggered by the impact of meteoric water recharge, our numerical simulations show that the hydraulic pressure gradient at depth was at a maximum during the period of 2010–2019, just before the seismic event. The estimated overpressure at the intersection of the two faults, which is the most probable place of the hypocenter, was close to 1 MPa. This hydraulic effect is about two and a half times larger than the cumulative effect of mechanical stress release due to the mass removal from the surface quarry over the two past centuries. This work suggests a rapid hydraulic triggering mechanism on a network of faults at a shallow depth after a heavy rainfall episode.

1. Introduction

Large earthquakes usually occur along preexisting faults and plate interfaces. However, intraplate earthquakes are difficult to assess, as many damaging earthquakes are not associated with the known major faults, which are considered to have the highest seismic potential in the area [1]. Since the recurrence time of intraplate events is long, our knowledge and understanding of the fault dynamics (structure, rheology, stress loading, and interaction) are still limited, and causes other than the long-term tectonic stress loading are, therefore, considered for some earthquakes. For example, the 2008 7.9 Mw Wenchuan (China) earthquake had a total fault length of more than 200 km in the Longmenshan fault zone. Before the occurrence of the earthquake, the highest seismic potential of the area had never been attributed to the ruptured faults (causal faults) from the seismic hazard assessment [2] view point. Although the tectonic stress loading is undoubtable over the whole area, the nucleation process of this mega earthquake has been discussed in relation to the nearby Zipingpu reservoir in terms of the elastic stress change and pore pressure change [3,4,5,6,7,8]. Indeed, any positive perturbation of stress on a causal fault can be suspected of triggering an earthquake [9]. The lack of in situ measurements, however, does not allow any definitive conclusion, and the impoundment of the reservoir may have activated the shallow micro-seismicity within a few kilometers below the dam [5,6], but the link to the hypocenter of the earthquake more than 10 km away is not clear.

The anthropogenic influence on earthquake triggering has been widely studied, and several authors have produced an overview of the likely cases [10,11,12,13,14,15], covering a range of magnitude between 1 and 8. At a local scale, the micro-seismicity at Gardanne, southern France, is correlated to the flooding of the underground abandoned mining gallery, with a time lag of about ten days [16]. The driving mechanism behind the triggering is not only human-driven, but it can also be related to natural variations on the Earth’s surface, namely climate variations [17,18,19]. It is reported that the seismicity in Himalaya has a seasonal trend according to the annual monsoon season, namely large amounts of precipitation in the summer [20,21]. Among the studies analyzing the rainfall effect, the seasonal pore pressure evolution was discussed through fluid diffusion in the limestone of southeastern Germany [19]. The seismicity triggered by rainfall in the karstic domain, in Switzerland, was studied through a fluid diffusion model in a poro-elastic context [22]. The hypothesis of “hydro-seismicity” developed by John K. Costain [23,24,25,26] attributes most intraplate and near-intraplate earthquakes to the dynamics of the hydrologic cycle. Such hydraulic perturbations may occur from a few to 10 km away if a permeably connected fault system exists. In France, a correlation between heavy rainfall and small earthquakes was shown in the Western Provence around the Nîmes Fault [27] and in the Provence Alps at Castellane [28].

The 2019 4.9 Mw Le Teil (France) earthquake heavily damaged nearby areas [29,30]. Regardless of its moderate magnitude, this earthquake ruptured the shallowest part of the known fault (only the first 2 km depth at most) and showed rupture traces on the ground surface (Figure 1). The area had been known for some historical earthquakes; however, earthquakes of this magnitude with surface ruptures had hardly been taken into account in local/regional seismic hazard assessments [31]. Previously, some authors pointed out that a nearby limestone quarry may have contributed to the stress loading on the causal fault [32,33,34]. The best-inferred epicenter is probably located not inside but rather southwest of the surface quarry, using the seismograms available from the mainshock and aftershocks [35]. In contrast to a purely mechanical view, here, we will investigate the hypothesis of an earthquake triggered by the water transfer from the ground surface. Indeed, the studied area suffered from heavy rainfall during the month before the seismic event. Therefore, a permeably connected fault system may play a role of conducting the pore pressure change at depth. We focus on the local hydraulic system in the study area. The movement of moisture in partially saturated media is simulated using a 3D diphasic flow, double-permeability model, with the soil moisture data recorded during the period of 2010–2019 as surface boundary and the Rhône River as edge boundary conditions. We will finally discuss the possible triggering mechanism by comparing the results of the hydraulic model with those of a mechanical model that simulates the mass withdrawal due to the quarry exploitation in a similar geological configuration. We will try to answer two key questions: (1) How large is the hydraulic overpressure due to the meteoric water recharge compared to the Coulomb stress change due to the mass withdrawal from the surface quarry? (2) Is the estimated location of the maximum hydraulic overpressure consistent with the estimated hypocenter location?

2. Materials and Methods

2.1. Differential Synthetic-Aperture Radar Interferometry (DInSAR) Using Sentinel-1 Data

Spaceborne differential SAR interferometry (DInSAR) has been widely used during the past decades to track land subsidence or uplift related to groundwater extraction or underground gas storage [37]. The same method has also been successfully used for identifying ruptures due to earthquakes and quantifying the co-seismic motion [38,39]. Sentinel-DInSAR was applied to measure the surface displacement along the sensor’s Line of Sight (LOS), which is the sensor-to-target direction. This method measures the projection of real surface motion along the LOS and provides 1D displacement measurements. These displacements are relative in space and time, as they are spatially related to a reference point, and temporally to the date of the first available satellite acquisition. In order to reduce the loss of coherence effect, four interferograms with short six-day timespans around the date of 11 November 2019 were produced using Sentinel-1 data (Table S1). The processing is based on the Gamma processing software (https://gamma-rs.com, accessed on 16 January 2021). Only one interferogram (named A059—orbit 59 in ascending mode) resulted as interpretable because of a poor coherence on the surface rupture zones for the three others. In order to interpret this interferogram for identifying and quantifying surface ruptures, an additional unwrapping step is required (Figure 2). For this step, we used the Minimum Cost Flow procedure implemented in Gamma [40].

The visual examination allowed a first estimation of the LRF rupture location and the positions of the extremities of a candidate for the BRF rupture (Figure 3). In order to obtain additional candidates, we added the positions of faults extracted from a 1:50,000 geological map [36]. These faults were imported in the tool for profile stacking and displacement estimation using the Cosi-corr software [41,42], in order to be applied to our unwrapped interferogram. Figures S1–S3 illustrate the use of the tool on different parts of LRF and BRF. Twenty lateral profiles were automatically generated by the tool, perpendicularly to the candidate on LRF/BRF, and three were manually added on BRF. Our objective was first to validate points on the fault candidate as reliable observations if significant differential motion between each side of the profile was observed, and then to quantify this motion. In addition, if the “jump” on the displacement profile is not exactly on the candidate’s position, this procedure allows to adjust the position by displacing the candidate according to the jump’s position. Finally, the obtained points were connected in order to obtain a continuous rupture trace. This proposed procedure was found to be sensitive enough for interpreting the initial interferometric information, and the obtained results were in fairly good agreement with the surface rupture evidence (Figure 3). Although it could not be fully exhaustive and minor motions could be missed, this method provided an accurate and reliable representation of the surface traces of LRF and BRF, and a quantification of their surface displacements was proposed (Figure 3).

Furthermore, some unwrapping issues can occur close to the ruptures for two main reasons. First, some sectors of the area have poor coherence because of possible surface changes that occurred during the six-day timespan due to the earthquake itself or due to the presence of locally vegetated land covers. Secondly, the observed motion on the ruptures was larger than quarter of the wavelength (i.e., 14 mm). One noteworthy point is the fact that the two parallel ruptures introduced a specific unwrapping issue (illustrated in Figure S4). This may have influenced the location and quantification of the rupture traces. Examples of unwrapping issues can be found in [43,44]. For these reasons, it is important to choose an interpretation of the interferogram consistent with the prior knowledge of faults (e.g., ground observations or boreholes). The consequence is that it introduces an ambiguity on the distribution of the measured slip between the two faults. As this ambiguity cannot be resolved only on the basis of the information of one interferogram, here, we will use additional observations (i.e., surface rupture evidence and boreholes’ cores).

2.2. Hydraulic Model Using ComPASS

ComPASS is an open platform using state-of-the-art numerical schemes to discretize multiphase Darcian flows on generic unstructured meshes [45,46]. We adopted a so-called hybrid dimensional model coupling a 3D model of the “matrix” with a 2D model in “fault planes” using ComPASS (Appendix A).

2.2.1. Hydraulic Parameters in Matrix/Fault

The hydraulic parameters in the Barremian/Urgonian limestones are highly variable in the host rock, the damaged zone, and the core fault [47,48,49,50]. The continuous medium (“matrix”) and the fault elements are characterized by a large range of porosity and permeability. In the Urgonian carbonates at Low-Noise Underground Laboratory (LSBB) of Russel, about 90 km southeast of Le Teil, the observations showed the presence of discontinuities (joints, veins, faults, and stylolites) that influence the hydraulic properties from the core to the reservoir scale. The measured porosity varied from 1% to 20% and the permeability varied in a range between 10⁻¹⁷ m² and 5 × 10⁻¹² m² close to the fault core [47]. In the “matrix”, a permeability of 10⁻¹⁶ m² and a porosity of 20% (

Table 1. Base cases using SM30 at a 30 cm depth (Berzème) (parameters and results).

Base Case	BC16	BC20	BC23	BC24
Surface condition	SM30	SM30	SM30	SM30
Matrix porosity, ${\mathsf{\theta }}_m$	0.2	0.2	0.2	0.2
Matrix permeability, ${\mathrm{K}}_m$	10−18 m2 in Apto-albien	10−16 m2	10−18 m2 in Apto-albien	10−18 m2 in Apto-albien
	10−16 m2 elsewhere		10−16 m2 elsewhere	10−16 m2 elsewhere
Fault porosity, ${\mathsf{\theta }}_f$	0.1	0.1	0.1	0.1
Fault permeability, ${\mathrm{K}}_f$	10−11 m2	10−11 m2	5 10−12 m2	10−12 m2
Fault width, $W$	20 m	20 m	20 m	20 m
Maximum differential of pressure (ΔP) along intersection LRF/BRF	0.98 MPa (9.84 bar)	0.97 MPa (9.75 bar)	0.84 MPa (8.39 bar)	0.38 MPa (3.8 bar)

) were chosen, corresponding to typical values in the host rock measured in the group of samples with higher porosity and permeability. In the “fault”, the fault permeability varied in the range of high values between 10⁻¹² m² and 10⁻¹¹ m² based on in situ measurements in fault zones [48]. The hydraulic parameters are displayed in Table 1 for the base cases using the in situ soil moisture at a 30 cm depth at Berzème (SM30), and in

Table A1. Additional cases using surface soil moisture (SSM) of the SMOS satellite.

Sensitivity Case	SC21	SC22
Surface condition	SSM (SMOS-CATDS ASC, L2 cell, 3 days)	SSM (SMOSMAP-IB ASC, L2 cell, 3 days) *
Matrix porosity, ${\mathsf{\theta }}_m$	0.2	0.2
Matrix permeability, ${\mathrm{K}}_m$	10−18 m2 in Apto-albien	10−18 m2 in Apto-albien
	10−16 m2 elsewhere	10−16 m2 elsewhere
Fault porosity, ${\mathsf{\theta }}_f$	0.1	0.1
Fault permeability, ${\mathrm{K}}_f$	10−11 m2	10−11 m2
Fault width, $W$	20 m	20 m
Maximum differential of pressure (ΔP) along intersection LRF/BRF	0.9 MPa (9.03 bar)	0.87 MPa (8.73 bar)

* SMOSMAP-IB data were produced and shared by INRAE BORDEAUX.

for the additional cases using the surface soil moisture acquired by the SMOS satellite (SSM).

2.2.2. Soil Moisture (SM30) Data at the Berzème Station

The SMOSMANIA network (Soil Moisture Observing System) is based on the Meteorological Automatic Network Integrated Application of Météo-France. The stations form a Mediterranean–Atlantic transect following the marked climatic gradient between the two coastlines. The station at Berzème of SMOSMANIA is located at less than 15 km from Le Teil quarry (Figure A1). The vegetation on these sites is made up of natural fallow land, cut once or twice a year. Since 24 April 2015, four soil moisture probes have been installed per station at depths of 5, 10, 20, and 30 cm. These capacitance probes use the dielectric permittivity properties of the soil to estimate the volumetric soil moisture content. The data at a depth of 30 cm (noted SM30) are used in the reference ComPASS simulations as boundary conditions for the whole nodes at the top surface, except for those belonging to the Rhône River. The soil moisture content is the quantity of water contained in the soil. The normalized water content (or effective saturation, Se) is calculated at the Berzème station following Equation (1):

$$\mathrm{S}\mathrm{e}=\frac{\left(\mathrm{S}\mathrm{M}30-{\mathsf{\theta }}_{\mathrm{r}}\right)}{\left(\mathsf{\omega }-{\mathsf{\theta }}_{\mathrm{r}}\right)},$$

(1)

where SM30 is the volumetric water content at a 30 cm depth (raw data), ${\mathsf{\theta }}_{\mathrm{r}}$ is the residual water content (about 12% between 2015 and 2019), and the saturated water content is equivalent to porosity, ω (about 42% at 30 cm). SMOSMANIA was developed to validate remote sensing and model soil moisture estimates. The average distance between two neighboring stations is approximately 40 km, which is consistent with the spatial resolution of remote sensing soil moisture products of the SMOS satellite.

2.2.3. Surface Soil Moisture (SSM) Products Acquired by the SMOS Satellite

The first satellite mission to focus primarily on the collection of soil moisture data was the European satellite SMOS (Soil Moisture and Ocean Salinity), launched in November 2009. Here, we use the term surface soil moisture (SSM) to refer to the volumetric soil moisture in the first few centimeters (0–5 cm) of the soil. The soil moisture data acquired by SMOS are used as alternative surface boundary conditions (Appendix A). The SMOS-CATDS (Centre Aval de Traitement des Données SMOS) provides either a 3-day product or a 10-day SSM product (that contains median, minimum, and maximum values of soil moisture). Ascending and descending overpasses of the SMOS satellite are bound to show different values of the retrieved parameters that may not always be comparable, and they are, thus, separately retrieved. The data are presented over the Equal-Area Scalable Earth (EASE grid 2) [51], with a sampling of about 25 km × 25 km, and the studied area is included in two grid cells, called L1 and L2 (Figure A1). Using the Berzème station during the year 2019, we found a bias of −12.3 vol.% and a correlation coefficient of 0.49, as already observed in southwestern France by others [52]. As the residual water content, ${\mathsf{\theta }}_{\mathrm{r}}$, is almost zero for all three-day SSM products, the effective saturation, Se, is calculated following Equation (2) (Figure S6):

$$\mathrm{S}\mathrm{e}=\frac{\mathrm{S}\mathrm{S}\mathrm{M}}{\mathsf{\omega }}$$

(2)

where ω is the porosity at 5–10 cm (about 50% in the Harmonized World Soil Database). Another SSM product, called SMOSMAP-IB, is available at INRAE BORDEAUX [53]. It fuses SMOS and NASA’s SMAP satellite. We found a much better correlation coefficient of 0.7 for SMOSMAP-IB than for SMOS-CATDS. Unbiased values of Se are then calculated following Equation (3) (Figure A2):

$$\mathrm{S}\mathrm{e}=\frac{\left(\mathrm{S}\mathrm{S}\mathrm{M}+\mathrm{B}\mathrm{I}\mathrm{A}\mathrm{S}\right)-\mathrm{B}\mathrm{I}\mathrm{A}\mathrm{S}}{(\mathsf{\omega }-\mathrm{B}\mathrm{I}\mathrm{A}\mathrm{S})}=\frac{\mathrm{S}\mathrm{S}\mathrm{M}}{(\mathsf{\omega }-\mathrm{B}\mathrm{I}\mathrm{A}\mathrm{S})}$$

(3)

where BIAS is the bias between SSM and SM30 during the year 2019 (−11.3 vol.%).

2.3. Mechanical Model Using 3DEC^TM

To model the mechanical effect of mass withdrawal on the fault system, the Distinct Element Method of 3DEC^TM code (Version 5.2, Itasca Consulting Group Inc., Minneapolis, MN, USA), that explicitly handles discontinuities as mechanically active joints, was adopted here [54]. The Coulomb stress change is given by $\Delta CFF=\left|\Delta \tau \right|-\mu \Delta {\sigma }_n$, where $\mathsf{\Delta }\mathsf{\tau }$ and $\mathsf{\Delta }{\mathsf{\sigma }}_{\mathrm{n}}$ are the shear and normal stress changes (positive in compression), and $\mathsf{\mu }$ is the frictional coefficient. The direction of $\mathsf{\tau }$ is taken for the maximum shear stress on the given fault geometry. The mass withdrawal generates a relaxing of normal stress on LRF as well as an increase of shear stress. The Coulomb stress change, $\mathsf{\Delta }\mathrm{C}\mathrm{F}\mathrm{F}$, related to the mass withdrawal is estimated from the difference between the two equilibrium steps (Appendix B).

2.4. Seismological Data Analysis Using the Vibration Sensor at Clauzel House (CLAU)

A vibration sensor was installed by the quarry owner in the private house Clauzel (CLAU, red triangle in Figure 1) to monitor the vibrations due to the quarry blasts. The sensor is a three-component, short-period seismograph (sampling rate at 1024 Hz). The recorded data of the mainshock include visually unnatural jumps in velocity, and this leads to unexpected levels of acceleration. The on-site visit leads us to think that the CLAU sensor has not been correctly fixed on the house floor and probably may have been impacted by the fall of miscellaneous objects around it. Although the whole waveform may not be exploitable, the first movement at the beginning of the signals could be informative. In order to verify the polarity, we checked the blast signal of 25 September 2019, for which the source location is well-known. For the given records, we removed the linear trend, applied the Butterworth bandpass filter (order of 8) between 1 and 10 Hz, and integrated once using the software SeisGram2K Seismogram Viewer v7.0.0 × 10 (www.alomax.net, accessed on 16 January 2021) for data viewing and processing. Then, we manually exploited the particle motion of this blast for a selected time window. We obtained a back azimuth of N98°E ± 20° for the true value of N111°E (Figure S7). Thus, the particle motion approximatively indicates the event direction with a margin of error of around 16°. The sensor data were used to estimate the azimuth of the mainshock of 11 November 2019, assuming the same margin of error.

3. Results

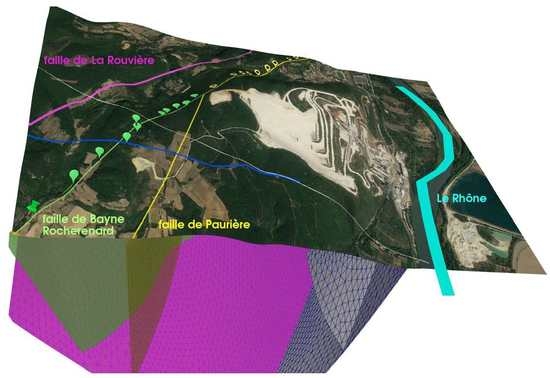
3.1. Geological Context around the Fault System

The concerned area is located in the Rhône Valley in southeastern France near Montélimar City (Figure 1). The Urgonian limestones, which were extracted from the nearby quarry, were deposited in the early cretaceous epoch, during the Upper Barremian–Lower Aptian age, and afterwards, some calcareous marlstones were deposited during the Aptian–Albian age, east of La Rouvière fault (LRF) (Figure 1). The available geological map [36] of the studied area at a scale of 1:50,000 shows the existence of several, mostly NE–SW, striking fault segments in the area. The observed surface rupture was consistent with the portion of the already mapped La Rouvière fault (LRF) [31]. Each other segment of the geological map [36] was then analyzed by using the differential SAR interferometry (DInSAR) method applied to Sentinel-1 images (Section 2.1, Figure 2).

3.2. Surface Traces of the Fault System Using DInSAR

We aimed to refine the location of surface ruptures with a particular interest in La Rouvière fault (LRF) and the surrounding ones mapped on the 1:50,000 geological map [36]. To carry out this analysis, four interferograms were produced using SAR data acquired by Sentinel-1 (Table S1). After visual analysis of the four produced interferograms, only the track A059 had sufficient quality in the area of major deformation. The interpretation of this interferogram is shown in Figure 2 and provided in the Supplementary Materials. The final geocoded product had 15 m spatial sampling. While the main rupture along LRF was clearly identified on the A059 interferogram, a secondary rupture could be suspected from the pattern of the deformation at the extremities of the ruptured area (Figure 2c,d). The latter mostly coincided with the mapped Bayne Rocherenard fault (BRF) in the southwestern area of the studied area, and this continued in the northeastern direction, always parallel to the LRF, after the intersection with the Paurière fault (PF) (Figure 2e). The interferometric coherence was better on the southwestern part of the BRF than on its northeastern part (more black pixels). Figure 3 compares the identified positions with the cartographic representation of the faults as well as the differential motion along the rupture traces. The main rupture along LRF exhibited motion up to 14 cm in the line of sight (LOS) in the central part of the rupture (points LRF5 to LRF14, between 1000 and 3000 m). The LRF motion moved more on the central part of the rupture (points LRF5 to LRF14, between 1000 and 3000 m). These results are consistent with previous results in [31]. In contrast, the differential motion along BRF was estimated up to 4 cm, about one-third of the main motion along LRF (Figure 3b). The southwestern part along BRF (BRR1 to BRR10, between 2000 and 3800 m) moved two times less (about 2 cm) than the northeastern part (BRR11 to P8, between 3900 and 5400 m). Our interferogram interpretation suggests the re-positioning of the northeastern part of BRF. Most of the observed surface rupture evidence found in [31] was close to LRF from the geological map [36], except for one, which was found near the point P7 along the northeastern extension of the BRF trace we found (Figure 3). Using this DInSAR analysis, we reconstructed the local fault system: The trace of BRF did not intersect with LRF on the ground surface. BRF, however, remained secondary in terms of the differential displacement during the earthquake. The newly processed seismic cross-section M201 allowed us to also propose a local 3D geometry.

3.3. Three-Dimensional Geometry of the Three-Fault System Using M201 Cross-Section

Since our main objective was to calculate the influence of water and stress transfers from the ground surface, we only focused on the local shallow 3D structure that includes, from west to east, La Rouvière (LRF), Bayne Rocherenard (BRF), and Paurière (PF) faults (Figure 3). In order to clarify the possible connectivity of these faults, the seismic cross-section M201 was re-interpreted. This profile, M201, was acquired by the CGG company during 1962 to 1963 (available on www.minergies.fr, accessed on 15 June 2020). LRF is a southeast dipping fault, consistent with the focal mechanism and finite source inversions of Le Teil earthquake [32,35]. The seismic cross-section indicates that BRF was branching from LRF and PF was branching further from BRF (Figure 4). Assuming the dip angles were approximately constant, the position of each fault on the ground surface allowed us to estimate the dip angles (Texts S1–S3). We found a true dip angle of 54° for LRF. Our value is consistent with the best-fitting dips for InSAR data inversion in the range of 54°–59° found previously in [55].

This shaped the 3D geometry of the three-fault system at the local scale. The modeling volume includes the three-fault system (LRF, BRF, and PF) as well as two other dipping faults of our geological model close to the Rhône River (Figure 5). This fault system is part of a 3D geological model at a regional scale (up to 100 km horizontally and down to a 5 km depth) based on the Valvignères exploration well (Figure A1) [56].

Additional data support this 3D local fault model. The SC03 borehole drilled by the quarry owner in 2016 is near the point P0 of the new BRF trace (Figure 3a). An important quantity of water was lost at an 83 m depth during the SC03 geotechnical (personal communication of the quarry owner). Moreover, the SC03 core samples showed, at a 90.5 m depth, a near-vertical natural fracture with calcite veins, and at a 112.5 m depth, the geological evidence for fluid overpressures, with angular fragments organized in a jigsaw puzzle pattern (Figure S5). Both observations are consistent with an intersection of the borehole SC03 with a fault (the northeastern part of BRF) (Text S3). Moreover, we inferred that the BRF fault zone may form a drain along the fracture network, leading to fault-parallel flows.

3.4. Hydraulic Simulations Using ComPASS

Several authors have tested whether or not any correlation could exist in geological environments with fractured or karstified limestones between the seismicity and the local hydrology (river discharge) [28] or the meteorology (rainfall) [19]. A significant percentage of high discharges was followed by at least one seismic event within a 7–28-day optimal interval in [28], while a maximum correlation with the rainfall data was shown if the seismicity was shifted backwards by 8 days in [19]. First, we have compared the daily rainfall and the mean daily discharge of Le Rhône to the seismic events in a rectangular area of 50 km × 25 km around the Teil during the period 2010–2019 (Figure A1). Seismic data were collected from the French national seismic monitoring network (RéNaSS) and rain data from Météo-France weather station at Montélimar (44.58° N, 4.74° E). Three of the four most intense rainfall events between 2010 and 2019 (4 May 2010, 4 November 2014, 24 October 2019) were followed by a seismic event, which occurred between 8 and 18 days after the date of the extreme rainfall (Figure A1b). However, a statistical analysis was not possible here because the number of seismic events is too limited (only 12). Therefore, we adopted a numerical approach to specifically simulate the pore pressure at depth during 2010 to 2019 (Section 2.2, Appendix A).

Using the local 3D geometry (Figure 5), the pressure variations at depth linked to the infiltration of meteoric water in the period preceding the earthquake were simulated by a double-permeability model using ComPASS (Section 2.2.1). In order to exclude as much of the evapotranspiration and surface runoff contributions as possible, the soil moisture data at a 30 cm depth (SM30) at Berzème station were used instead of the rainfall data in all reference simulations (Section 2.2.2). The variations of effective water saturation at the ground surface (Figure 6), occurring over time, result in piezometric level changes. More specifically, an increase of water saturation at the top of the model, which was related to rainfall events, resulted in overpressure pulses from the surface towards a greater depth. The surface soil moisture (SSM) data acquired by the SMOS satellite were also used in additional simulations to extend the simulating period between 2010 and 2015 (Figure A2, Section 2.2.3). The soil moisture data (SM30 or SSM) were used as input for the nodes at the top surface, except for those that belonged to the Rhône River, where a constant/fixed boundary condition was applied (Appendix A).

The hydraulic parameters in the Barremian/Urgonian limestones are highly variable (Section 2.2.1). For the “fault”, a homogeneous high fault permeability value of 10⁻¹¹ m² (i.e., a hydraulic conductivity of k ~10⁻⁴ m s⁻¹ at a 500 m depth) and a mean fault porosity of 10% were chosen to explore the infiltration in a highly conductive, intensively fractured fault zone, that is representative of fast fluid conduits in the shallow subsurface. Such high permeability values are expected in the porous layers along the fault zones in these limestones [47,48]. In particular, measurements in Barremian/Urgonian limestones showed an average permeability of 7 10⁻¹² m² at Russel (about 90 km southeast of Le Teil) [48]. These hydraulic parameters were used for the reference simulations and a sensitivity analysis was also carried out by varying the fault permeability (Table 1).

In the reference case noted as BC16, the date of 24 September 2019 corresponds to a relative minimum pressure before the seismic event, as shown in Figure 7d. The differential of pressure (ΔP) for the period preceding the earthquake (between 24 September and 11 November 2019) is shown in Figure 7a–c. A peak value of ΔP of 0.98 MPa (984 kPa or 9.8 bars) appeared along the intersection line between BRF and LRF (Figure 7c). This maximum pore overpressure appeared near the junction of the three-fault system at around a 1200 m depth (Figure 7b). This value is higher than the peak value along the intersection line between PF and LRF. Moreover, the pressure gradient for the previous 30 days was at a maximum just before the earthquake of 11 November 2019 (about 18 days, in Figure 7d).

We verified via the double-permeability model that the intersections between two or multiple faults were the most probable location zones for the hypocenter of an earthquake triggered by a hydraulic recharge, according to the “hydro-seismicity” concept developed by J.K. Costain in [26]. In BC16, we assumed a 100-fold decrease of the permeability in the Apto-Albian marlstone layer in comparison to the Upper Barremian limestone layer (i.e., 10⁻¹⁸ m²) (Table 1). Another case, called BC20, corresponds to a simplified scenario with a homogeneous permeability of 10⁻¹⁶ m² in the matrix in the shallow subsurface. We obtained a differential pressure, ΔP, of about 0.975 MPa. This counterintuitively indicates that the surface clays did not play a predominant role in establishing the hydraulic overpressure on LRF at depth. Indeed, the overpressure was qualitatively stable since the overpressure was transported principally in this model by BRF to the depth.

A limit of this model is that the fault permeability is assumed constant over time. A recent in situ experiment in [48] measured a 14-fold increase of the fault permeability during the aseismic period after an overpressure of about 1.7 MPa. Therefore, a sensitivity analysis has been carried out on the fault permeability (BC23 and BC24 in Table 1). In BC24, we found that a 10-fold decrease of fault permeability corresponded to a 2.6-fold decrease of the overpressure (0.38 instead of 0.98 MPa).

Finally, we carried out two additional simulations, replacing SM30 with SSM values to extend the simulated period between 2010 and 2019 (SC21 and SC22 in Table A1). The use of SSM instead of SM30 decreased the simulated overpressure at depth by less than 11.2% (0.87 instead of 0.98 MPa in Table A1). This decrease is consistent with the lower SSM values compared to the in situ soil moistures at a 30 cm depth before the earthquake (Figure A2a). An absolute maximum pressure gradient during the extended period of 2010–2019 was also predicted by our model just before the earthquake (Figure A2).

4. Discussion

Our hydraulic simulations showed that the pore pressure change may reach 0.98 MPa at a depth of around 1.2 km at the intersection of the local three-fault system. It is thus naturally questioned how this is significant compared to the mechanical impact due to the mass removal of the nearby Le Teil surface quarry. Prior analytical evaluation of Coulomb stress, based on Boussinesq solution in a homogeneous half-space elastic medium, showed variations of 0.15 to 0.2 MPa [32,57]. It is important to note that the earlier amplitude value of about 1 MPa proposed by De Novellis et al. in [34] was later corrected in [57]. We performed 3D mechanical simulations using 3DEC^TM distinct-element code [54] to represent an improved local geological model, including discontinuities as well as lithology in a 3D medium (Section 2.3). The Coulomb stress change, ΔCFF, was simulated by 3DEC^TM on all the considered fault segments (Figure A3). The spatial distributions of $\mathsf{\Delta }{\mathsf{\sigma }}_{\mathrm{n}}$ and $\mathsf{\Delta }\mathsf{\tau }$ on LRF are shown in Figure 8c,d, respectively. ΔCFF showed a maximum change of 0.25 MPa at around a 1 km depth on LRF (Figure 8b), a value of the same order as the Boussinesq solution [32,57]. When we look carefully at the LRF, one peak (0.25 MPa) exists above the intersection with BRF, while another peak (0.24 MPa) appears along the intersection of LRF and BRF. An important portion of shear stress on LRF was generated along the fault line between LRF and BRF (pan Figure 8d). Additionally, the maximum value of ΔCFF among all the faults appeared not on LRF but on BRF (0.39 MPa). It is worth noting that the mechanical stress change can be larger around the intersection of LRF and BRF, and that BRF is more favorably located than LRF in terms of the mechanical stress change. This mechanical term $\mathsf{\Delta }\mathrm{C}\mathrm{F}\mathrm{F}=\left|\mathsf{\Delta }\mathsf{\tau }\right|-\mathsf{\mu }\mathsf{\Delta }{\mathsf{\sigma }}_{\mathrm{n}}$, should then be compared to the hydraulic term. The hydraulic term may be included in the calculation of the Coulomb stress change following $\mathsf{\Delta }\mathrm{C}\mathrm{F}\mathrm{F}=\left|\mathsf{\Delta }\mathsf{\tau }\right|-\mathsf{\mu }(\mathsf{\Delta }{\mathsf{\sigma }}_{\mathrm{n}}$ − $\mathsf{\Delta }\mathrm{P})$, where $\mathsf{\Delta }\mathrm{P}$ is the difference of pore water pressure, previously calculated by ComPASS. The reference simulation BC16 highlighted that the hydraulic term, $\mathsf{\mu }\mathsf{\Delta }\mathrm{P}$ (0.59 MPa), was about two and a half times larger than the maximum mechanical stress change due to the mass removal from the ground surface (0.24 MPa). Moreover, the mechanical unloading is a long-term, quasi-static process, lasting over nearly 200 years, while the overpressure pulse on faults is a dynamic process shortly preceding the earthquake of 11 November 2019.

The second key question in the discussion is the comparison of the overpressure locations with other hypocenter locations using independent approaches. Before the earthquake, the studied area had not been covered by a dense seismic network. The closest station of the permanent network is far from the source area, by about 30 km (OGLP stations from https://seismology.resif.fr/, accessed on 15 June 2021), and thus the hypocenter location using any catalogue has a significant uncertainty (of several km). However, a local network was installed just after the seismic event, and the hypocenter has recently been relocated using multiple approaches [35]. The most probable hypocenter location using the calibration from aftershocks is at 44.5188N, 4.6694E, and a 1.3 km depth, with an error of about 500 m. This epicenter position is very close to the surface projection of the intersection of LRF and BRF (Figure 8 and Figure 9). It is also close to the projected locations of the maximum overpressures of both BC16 and BC20 reference simulations. A nearby blast monitoring station, CLAU, recorded the mainshock (Figure 9). Although this short-period sensor calibrated for micro-vibrations of quarry blasts was saturated during the mainshock, we found that the first particle motion could bring some useful information (Section 2.4, Figure S7). The azimuth and its associated uncertainty of the first-wave arrival of the mainshock was estimated as N164°E ±16° (Figure 9). This direction is consistent with the overpressure epicenter locations previously found by ComPASS. Observing this accordance between the seismological analyses and our hydraulic and mechanical modeling, we suggest that the causal fault is more complex than one single fault (LRF), and that the intersection of LRF and BRF played a role for the nucleation process. It is well-known that the nucleation process of an earthquake may occur around the geometrical irregularity of a complex fault system [58,59,60]. Our interpretation may also address the question of the indetermination of the dip angle for the mainshock (between 40° and 65°), as raised by Delouis et al. in [35]. The steeper BRF (69° dip) may have played a major role in the mainshock.

5. Conclusions

We compared two potential triggering factors for the earthquake of 11 November 2019 at Le Teil (France). We carried out two separate numerical approaches to simulate the impacts of water and stress transfers from the ground surface on the fault system at depth. We considered the double-surface rupture found by our DInSAR interpretation (BRF in addition to LRF) and a newly processed local seismic cross-section in order to shape the 3D geometry of the local three-fault system. The soil moisture data at the ground surface were used as surface boundary conditions of the hydraulic model during the period 2010–2019. The near-vertical BRF geometry became the major drain path of rainfall during the month before the earthquake, thus increasing the pore pressure at depth, enough to possibly trigger a very shallow earthquake on LRF. The simulated pore pressure at depth showed a local peak just before the 2019 Le Teil earthquake at the intersection of the two faults, BRF and LRF, very close to the hypocenter location determined by other seismological studies [35]. The estimated overpressure was close to 1 MPa, and this hydraulic effect was about two and a half times larger than the maximum stress change due to the mass removal of the nearby surface quarry. This work thus suggests a rapid hydraulic triggering mechanism at a shallow depth on a network of faults after a strong rainfall episode. Similar fault systems may be investigated in the near future to study the shallow, climatically modulated seismicity, with the challenging perspective of improving the local seismic hazard assessment in the intraplate domain.