Spectral Correlation and Spatial High–Low Frequency Information of Hyperspectral Image Super-Resolution Network
Abstract
:1. Introduction
- (1)
- Due to the different spectral curve responses corresponding to different pixels in HSI, an attention mechanism can be applied to the emphasis of spectral features. However, the existing spectral attention methods based on 3D convolution can only extract the features of several adjacent spectra or exchange a wider spectrum receptive field with a larger convolution kernel parameter. Furthermore, if two-dimensional spatial attention and channel attention are simply extended to three-dimensions, the information present in the spectrum dimension cannot be effectively exploited.
- (2)
- Most existing SR methods ignore the features of different stages, or only concatenate the features of different stages to the end of the network, without fully considering the further mining of the feature information of each stage in the existing model.
- (3)
- Most existing SR methods directly apply upsampling for SR reconstruction at the end of feature extraction, not considering the information fusion between features after feature extraction to achieve a more precise reconstruction performance.
- (1)
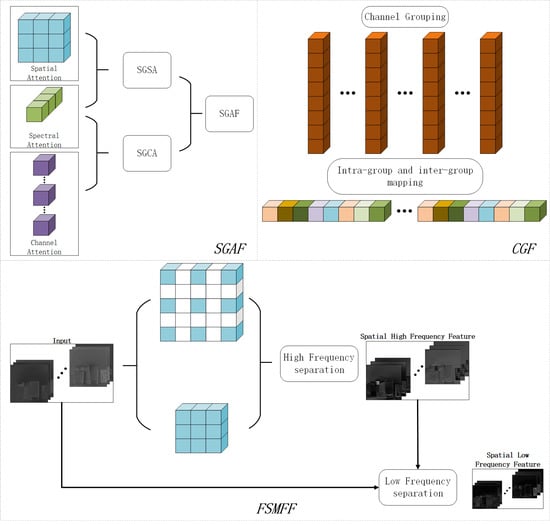
- The spectrum-guided spatial/channel attention (SGSA/SGCA) module use spectral high-frequency information to optimize channel attention and spatial attention, so that it can be applied in spectral dimension. The proposed attention module can simultaneously focus on the spatial, spectral, and channel features of HSI.
- (2)
- A cross-fusion module for joint spectral features (CFJSF) combines features from three branches and fuses them through multi-head self-attention, sharing the attention map with other branches. This module allows the network to learn the differences between response curves of different features in the spectrum dimension.
- (3)
- The high- and low-frequency separated multi-level feature fusion (FSMFF) is designed for merging the multi-level features of HSIs. This module enhances the expression ability of the proposed network.
- (4)
- Channel grouping and fusion (CGF) uses channel grouping to enable feature information in one group to guide the mapping and transformation of another group of feature information. Each group of features only affects the adjacent group of features, which allows the network to refine the extracted fusion feature information and transmit it to the final upsampling operation.
2. Proposed Method
2.1. Overall Framework
2.2. Spectral and Spatial Feature Extraction Module (SSFE)
2.3. High–Low Frequency Separated Multi-Level Feature Fusion (FSMFF)
2.4. Channel Grouping and Fusion (CGF)
3. Experiments
3.1. Datasets
3.2. Implementation Details
3.3. Results and Analysis
3.4. Ablation Study
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jalal, R.; Iqbal, Z.; Henry, M.; Franceschini, G.; Islam, M.S.; Akhter, M.; Khan, Z.T.; Hadi, M.A.; Hossain, M.A.; Mahboob, M.G.; et al. Toward Efficient Land Cover Mapping: An Overview of the National Land Representation System and Land Cover Map 2015 of Bangladesh. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3852–3861. [Google Scholar] [CrossRef]
- Zhong, P.; Wang, N.; Zheng, Z.; Xia, J. Monitoring of drought change in the middle reach of Yangtze River. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; Volume 2018, pp. 4935–4938. [Google Scholar]
- Goetzke, R.; Braun, M.; Thamm, H.-P.; Menz, G. Monitoring and modeling urban land-use change with multitemporal satellite data. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 8–11 July 2008; Volume 4, pp. 510–513. [Google Scholar]
- Darweesh, M.; Al Mansoori, S.; AlAhmad, H. Simple Roads Extraction Algorithm Based on Edge Detection Using Satellite Images. In Proceedings of the 2019 IEEE 4th International Conference on Image, Vision and Computing, ICIVC 2019, Xiamen, China, 5–7 July 2019; pp. 578–582. [Google Scholar]
- Kussul, N.; Shelestov, A.; Yailymova, H.; Yailymov, B.; Lavreniuk, M.; Ilyashenko, M. Satellite Agricultural Monitoring in Ukraine at Country Level: World Bank Project. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Waikoloa, HA, USA, 26 September–2 October 2020; pp. 1050–1053. [Google Scholar]
- Di, Y.; Xu, X.; Zhang, G. Research on secondary analysis method of synchronous satellite monitoring data of power grid wildfire. In Proceedings of the 2020 IEEE International Conference on Information Technology, Big Data and Artificial Intelligence, ICIBA 2020, Chongqing, China, 6–8 November 2020; pp. 706–710. [Google Scholar]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Hou, H.; Andrews, H. Cubic splines for image interpolation and digital filtering. IEEE Trans. Acoust. Speech Signal Process. 1987, 26, 508–517. [Google Scholar]
- Stark, H.; Oskoui, P. High-resolution image recovery from image-planear rays, using convex projection. J. Opt. Soc. Am. 1989, 6, 1715–1726. [Google Scholar] [CrossRef] [PubMed]
- Irani, M.; Peleg, S. Improving resolution by image registration. CVGIP: Graphcial Model. Image Process. 1991, 53, 231–239. [Google Scholar] [CrossRef]
- Schultz, R.R.; Stevenson, R.L. Extraction of high-resolution frames from video sequences. IEEE Trans. Image Process. 1996, 5, 996–1011. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; Volume 2016-December, pp. 1646–1654. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Mei, S.; Yuan, X.; Ji, J.; Wan, S.; Hou, J.; Du, Q. Hyperspectral image super-resolution via convolutional neural network. In Proceedings of the International Conference on Image Processing, ICIP, Athens, Greece, 7–10 October 2018; Volume 2017-September, pp. 4297–4301. [Google Scholar]
- Yang, J.; Zhao, Y.-Q.; Chan, J.C.-W.; Xiao, L. A Multi-Scale Wavelet 3D-CNN for Hyperspectral Image Super-Resolution. Remote Sens. 2019, 11, 1557. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Q.; Li, X. Exploring the Relationship Between 2D/3D Convolution for Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8693–8703. [Google Scholar] [CrossRef]
- Li, J.; Cui, R.; Li, B.; Li, Y.; Mei, S.; Du, Q. Dual 1D-2D Spatial-Spectral CNN for Hyperspectral Image Super-Resolution. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3113–3116. [Google Scholar] [CrossRef]
- Liu, D.; Li, J.; Yuan, Q. Enhanced 3D Convolution for Hyperspectral Image Super-Resolution. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2452–2455. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Q.; Li, X. Mixed 2D/3D Convolutional Network for Hyperspectral Image Super-Resolution. Remote Sens. 2020, 12, 1660. [Google Scholar] [CrossRef]
- Zhang, J.; Shao, M.; Wan, Z.; Li, Y. Multiscale Feature Mapping Network for Hyperspectral Image Super-Resolution. Remote Sens. 2021, 13, 4180. [Google Scholar] [CrossRef]
- Hu, J.; Jia, X.; Li, Y.; He, G.; Zhao, M. Hyperspectral Image Super-Resolution via Intrafusion Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7459–7471. [Google Scholar] [CrossRef]
- Liu, D.; Li, J.; Yuan, Q. A Spectral Grouping and Attention-Driven Residual Dense Network for Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7711–7725. [Google Scholar] [CrossRef]
- Wang, X.; Ma, J.; Jiang, J. Hyperspectral Image Super-Resolution via Recurrent Feedback Embedding and Spatial–Spectral Consistency Regularization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Li, J.; Cui, R.; Li, B.; Song, R.; Li, Y.; Dai, Y.; Du, Q. Hyperspectral Image Super-Resolution by Band Attention Through Adversarial Learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4304–4318. [Google Scholar] [CrossRef]
- Yan, Y.; Xu, X.; Chen, W.; Peng, X. Lightweight Attended Multiscale Residual Network for Single Image Super-Resolution. IEEE Access 2021, 9, 52202–52212. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 391–407. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; Volume 2016-December, pp. 1874–1883. [Google Scholar]
- Odena, A.; Dumoulin, V.; Olah, C. Deconvolution and Checkerboard Artifacts. Distill 2016. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon1, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Park, J.; Woo, S.; Lee, J.-Y.; Kweon, I.S. Bam: Bottleneck attention module. arXiv 2018, arXiv:1807.06514. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HA, USA, 21–26 July 2017; Volume 2017-January, pp. 2261–2269. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image Super-Resolution Using Dense Skip Connections. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; Volume 2017-October, pp. 4809–4817. [Google Scholar]
- Chen, Y.; Fan, H.; Xu, B.; Yan, Z.; Kalantidis, Y.; Rohrbach, M.; Shuicheng, Y.; Feng, J. Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 3434–3443. [Google Scholar] [CrossRef]
- Zhang, J.; Long, C.; Wang, Y.; Piao, H.; Mei, H.; Yang, X.; Yin, B. A Two-Stage Attentive Network for Single Image Super-Resolution. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 1020–1033. [Google Scholar] [CrossRef]

























| Scale | Methods | PSNR ↑ | MPSNR ↑ | SSIM ↑ | SAM ↓ |
|---|---|---|---|---|---|
| Bicubic | 40.330 | 39.500 | 0.9820 | 3.311 | |
| VDSR | 44.456 | 43.531 | 0.9895 | 2.866 | |
| EDSR | 45.151 | 44.207 | 0.9907 | 2.606 | |
| ×2 | MCNet | 45.878 | 44.913 | 0.9913 | 2.588 |
| ERCSR | 45.972 | 45.038 | 0.9914 | 2.544 | |
| MSFMNet | 46.015 | 45.039 | 0.9917 | 2.497 | |
| Ours | 46.240 | 45.240 | 0.9921 | 2.474 | |
| Bicubic | 34.616 | 33.657 | 0.9388 | 4.784 | |
| VDSR | 37.027 | 36.045 | 0.9591 | 4.297 | |
| EDSR | 38.117 | 37.137 | 0.9626 | 4.132 | |
| ×4 | MCNet | 38.589 | 37.679 | 0.9690 | 3.682 |
| ERCSR | 38.626 | 37.738 | 0.9695 | 3.643 | |
| MSFMNet | 38.733 | 37.814 | 0.9697 | 3.676 | |
| Ours | 38.848 | 37.897 | 0.9699 | 3.630 | |
| Bicubic | 30.554 | 29.484 | 0.8657 | 6.431 | |
| VDSR | 32.184 | 31.210 | 0.8852 | 5.747 | |
| EDSR | 33.416 | 32.337 | 0.9002 | 5.409 | |
| ×8 | MCNet | 33.607 | 32.520 | 0.9125 | 5.172 |
| ERCSR | 33.624 | 32.556 | 0.9113 | 5.114 | |
| MSFMNet | 33.675 | 32.599 | 0.9136 | 5.084 | |
| Ours | 33.723 | 32.638 | 0.9134 | 5.027 |
| Scale | Methods | PSNR ↑ | MPSNR ↑ | SSIM ↑ | SAM ↓ |
|---|---|---|---|---|---|
| Bicubic | 32.406 | 31.798 | 0.9036 | 4.370 | |
| VDSR | 35.392 | 34.879 | 0.9501 | 3.689 | |
| EDSR | 35.160 | 34.580 | 0.9452 | 3.898 | |
| ×2 | MCNet | 35.124 | 34.626 | 0.9455 | 3.865 |
| ERCSR | 35.602 | 35.099 | 0.9503 | 3.683 | |
| MSFMNet | 35.678 | 35.200 | 0.9506 | 3.656 | |
| Ours | 35.927 | 35.413 | 0.9540 | 3.627 | |
| Bicubic | 26.596 | 26.556 | 0.7091 | 7.553 | |
| VDSR | 28.328 | 28.317 | 0.7707 | 6.514 | |
| EDSR | 28.649 | 28.591 | 0.7782 | 6.573 | |
| ×4 | MCNet | 28.791 | 28.756 | 0.7826 | 6.385 |
| ERCSR | 28.862 | 28.815 | 0.7818 | 6.125 | |
| MSFMNet | 28.920 | 28.873 | 0.7863 | 6.300 | |
| Ours | 29.031 | 29.000 | 0.7943 | 5.873 | |
| Bicubic | 24.464 | 24.745 | 0.4899 | 7.648 | |
| VDSR | 24.526 | 24.804 | 0.4944 | 7.588 | |
| EDSR | 24.854 | 25.067 | 0.5282 | 7.507 | |
| ×8 | MCNet | 24.877 | 25.096 | 0.5391 | 7.429 |
| ERCSR | 24.965 | 25.190 | 0.5382 | 7.834 | |
| MSFMNet | 25.027 | 25.257 | 0.5464 | 7.449 | |
| Ours | 25.125 | 25.377 | 0.5553 | 7.404 |
| Scale | Methods | PSNR ↑ | MPSNR ↑ | SSIM ↑ | SAM ↓ |
|---|---|---|---|---|---|
| Bicubic | 30.509 | 30.497 | 0.9255 | 3.816 | |
| VDSR | 33.988 | 34.038 | 0.9524 | 3.258 | |
| EDSR | 33.943 | 33.985 | 0.9511 | 3.334 | |
| ×2 | MCNet | 33.695 | 33.743 | 0.9502 | 3.359 |
| ERCSR | 33.857 | 33.910 | 0.9520 | 3.220 | |
| MSFMNet | 34.807 | 34.980 | 0.9582 | 3.460 | |
| Ours | 35.914 | 35.033 | 0.9584 | 3.068 | |
| Bicubic | 29.061 | 29.197 | 0.7322 | 5.248 | |
| VDSR | 29.761 | 29.904 | 0.7854 | 4.997 | |
| EDSR | 29.795 | 29.894 | 0.7791 | 5.074 | |
| ×4 | MCNet | 29.889 | 29.993 | 0.7835 | 4.917 |
| ERCSR | 30.049 | 30.164 | 0.7899 | 4.865 | |
| MSFMNet | 30.140 | 30.283 | 0.7948 | 4.861 | |
| Ours | 30.388 | 30.489 | 0.8068 | 4.692 | |
| Bicubic | 26.699 | 26.990 | 0.5936 | 7.179 | |
| VDSR | 26.737 | 27.028 | 0.5962 | 7.133 | |
| EDSR | 27.182 | 27.467 | 0.6302 | 6.678 | |
| ×8 | MCNet | 27.201 | 27.483 | 0.6254 | 6.683 |
| ERCSR | 27.288 | 27.548 | 0.6276 | 6.611 | |
| MSFMNet | 27.334 | 27.586 | 0.6356 | 6.615 | |
| Ours | 27.384 | 27.590 | 0.6427 | 6.576 |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| CFJSF | ✗ | ✓ | ✓ | ✓ | ✓ |
| HFGSA | ✗ | ✗ | ✓ | ✓ | ✓ |
| FSMFF | ✗ | ✗ | ✗ | ✓ | ✓ |
| CGF | ✗ | ✗ | ✗ | ✗ | ✓ |
| PSNR | 45.516 | 45.744 | 45.998 | 46.150 | 46.240 |
| mPSNR | 44.574 | 44.776 | 44.983 | 45.144 | 45.240 |
| SSIM | 0.9911 | 0.9914 | 0.9917 | 0.9919 | 0.9921 |
| SAM | 2.602 | 2.573 | 2.521 | 2.491 | 2.474 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zheng, R.; Chen, X.; Hong, Z.; Li, Y.; Lu, R. Spectral Correlation and Spatial High–Low Frequency Information of Hyperspectral Image Super-Resolution Network. Remote Sens. 2023, 15, 2472. https://doi.org/10.3390/rs15092472
Zhang J, Zheng R, Chen X, Hong Z, Li Y, Lu R. Spectral Correlation and Spatial High–Low Frequency Information of Hyperspectral Image Super-Resolution Network. Remote Sensing. 2023; 15(9):2472. https://doi.org/10.3390/rs15092472
Chicago/Turabian StyleZhang, Jing, Renjie Zheng, Xu Chen, Zhaolong Hong, Yunsong Li, and Ruitao Lu. 2023. "Spectral Correlation and Spatial High–Low Frequency Information of Hyperspectral Image Super-Resolution Network" Remote Sensing 15, no. 9: 2472. https://doi.org/10.3390/rs15092472
APA StyleZhang, J., Zheng, R., Chen, X., Hong, Z., Li, Y., & Lu, R. (2023). Spectral Correlation and Spatial High–Low Frequency Information of Hyperspectral Image Super-Resolution Network. Remote Sensing, 15(9), 2472. https://doi.org/10.3390/rs15092472