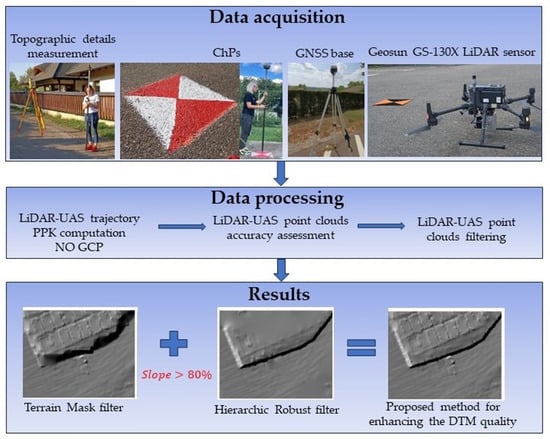
Enhancing LiDAR-UAS Derived Digital Terrain Models with Hierarchic Robust and Volume-Based Filtering Approaches for Precision Topographic Mapping
Abstract
:1. Introduction
- –
- Morphological-based filters: These algorithms use a structural parameter that describes the height differences within a threshold based on the horizontal distances used. The smaller the distance between a point and its neighbor, the smaller the height difference between them. A variant of this method is described in [15], in which the structural parameter depends on the terrain’s shape. Morphology-based filtering may be challenging in terrains with a variety of non-ground objects [16].
- –
- Surface-based filters: These algorithms work iteratively. In the first iteration, the lowest point for each grid cell is used to create an initial surface. Subsequently, residuals, which represent the distances between the measured points and the initial surface, are calculated. Each point is assigned a weight based on its residual value. Points with higher weights have a stronger influence on the surface, attracting the surface toward them, while points with lower weights have a lesser impact on the overall configuration of the surface. This iterative process continues until a stable surface is achieved, or the maximum allowable number of iterations is reached [18,19,20]. This type of method can present challenges in preserving terrain details, such as sharp ridges and cliffs. Additionally, it may have a tendency to misclassify small non-ground objects within the point cloud data [16].
- –
- Triangulated irregular network (TIN)-based refinement: An initial TIN is created based on the points with the lowest elevation in each grid cell. Gradually, other points are added by establishing reference thresholds [21]. This approach may encounter challenges when it comes to detecting discontinuous terrains, such as sharp ridges, and is time-consuming [16].
- –
- Segmentation and classification: These methods work with segments, which are classified based on height differences in their neighborhoods. In [22], a region growing technique of creating a surface was applied, based on height differences, to obtain segments that were subsequently classified into three categories: ground, buildings, and vegetation. In [23], segmentation compactness and height differences were applied to determine various types of areas, including the ground. Features such as geometry, radiometry, topology, the number of returns, intensity, and echo characteristics are used for better filtering ground points. These methods may encounter difficulties when applied to densely vegetated areas and strongly depend on the accuracy of segmentation [16].
- –
- Statistical analysis: These filters, particularly parameter-free algorithms, help minimize the need for manual parameter tuning, thus reducing uncertainty and enhancing the robustness of applying specific methods to different study sites. Additionally, these methods tend to excel in relatively flat terrains without intricate non-ground objects [16].
- –
- Multi-scale comparison: In general, this type of method operates through two main steps. First, several preliminary trend surfaces are created at different resolutions; second, each point in the point cloud is examined at various scales by comparing the elevation difference between the point and the different trend surfaces. This method is better suited for relatively flat terrains and may exhibit suboptimal performance in rapidly changing or complex landscapes [16].
Research Scope
2. Materials and Methods
2.1. Study Area
2.2. Research Methodology
2.3. Check Points (ChPs)
2.4. GeoSun GS-130X LiDAR Scanner
2.5. LiDAR-UAS Mission Planning
2.6. LiDAR-UAS Trajectory Computation
3. Results
3.1. Quality Assessment of the LiDAR-UAS Point Clouds
3.2. LiDAR-UAS Point Cloud Classification in Ground and Off-Ground Points
3.2.1. Cloth Simulation Filtering Approach
3.2.2. Volume-Based Filtering Approach
DSM Generation
Ground Point Filtering
3.2.3. Hierarchic Robust Filtering Approach
3.2.4. Proposed Method for Enhancing DTM Quality by Combining Robust Filtering and Volume-Based Filtering Approaches for Ground Points
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Component Name | System Parameters | |
|---|---|---|
| GS-130X | Weight | 1.26 kg |
| Measuring accuracy | Less than 0.1 m @120 m | |
| Working temperature | −20 °C~+65 °C | |
| Power range | 12 V–24 V | |
| Consumption | 10 W | |
| Carrying platform | GS-800 Multi Rotor and other brand | |
| Storage | 64 GB storage, maximum support 128 GB TF card | |
LiDAR Unit | Measuring range | 0.3 m–120 m@10% reflectivity |
| Laser class | 905 nm Class 1 (IEC 60825-1:2014) | |
| Channel | 32 channels | |
| Range accuracy | ±1 cm (typical value) | |
| Scanning frequency | 10 HZ, 20 HZ | |
| Data | Double echo 1,280,000 points/sec | |
| FOV | 360°, adjustable | |
| Laser sensor | HESAI Pandar XT | |
| POS unit | Update frequency | 200 HZ |
| Heading accuracy | 0.017° | |
| Pitch accuracy | 0.005° | |
| Rolling accuracy | 0.005° | |
| Position accuracy | ≤0.05 m | |
| GNSS signal type | GPSL1/L2/L5 GLONASSL1/L2 BDS B1/B2/B3 GAL E1/E5a/5b | |
| Pre-processing software | POS software | Output information: position, speed, attitude |
| Point cloud software | Output point cloud data format: LAS format, custom TXT format | |
| Camera (built-in) | FOV | 83 degrees |
| Effective pixel | 26 megapixels | |
| Focal length(mm) | 16 |
Appendix B


Appendix C


Appendix D


Appendix E

References
- Kucharczyk, M.; Hugenholtz, C.H.; Zou, X. UAV–LiDAR accuracy in vegetated terrain. J. Unmanned Veh. Syst. 2018, 6, 212–234. [Google Scholar] [CrossRef]
- Mandlburger, G.; Pfennigbauer, M.; Haring, A.; Wieser, M.; Glira, P.; Winiwarter, L. Complementing airborne laser bathymetry with UAV-based lidar for capturing alluvial landscapes. In Proceedings of the SPIE Remote Sensing, Toulouse, France, 14 October 2015. [Google Scholar]
- Seitsonen, O.; Ikäheimo, J. Detecting Archaeological Features with Airborne Laser Scanning in the Alpine Tundra of Sápmi, Northern Finland. Remote Sens. 2021, 13, 1599. [Google Scholar] [CrossRef]
- Herrault, P.-A.; Poterek, Q.; Keller, B.; Schwartz, D.; Ertlen, D. Automated detection of former field systems from airborne laser scanning data: A new approach for Historical Ecology. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102563. [Google Scholar] [CrossRef]
- Hodgetts, D. Laser scanning and digital outcrop geology in the petroleum industry: A review. Mar. Pet. Geol. 2013, 46, 335–354. [Google Scholar] [CrossRef]
- Wajs, J.; Trybała, P.; Górniak-Zimroz, J.; Krupa-Kurzynowska, J.; Kasza, D. Modern Solution for Fast and Accurate Inventorization of Open-Pit Mines by the Active Remote Sensing Technique—Case Study of Mikoszów Granite Mine (Lower Silesia, SW Poland). Energies 2021, 14, 6853. [Google Scholar] [CrossRef]
- Hollaus, M.; Mücke, W.; Roncat, A.; Pfeifer, N.; Briese, C. Full-Waveform Airborne Laser Scanning Systems and Their Possibilities in Forest Applications. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Managing Forest Ecosystems; Springer: Dordrecht, The Netherlands, 2014; pp. 43–61. ISBN 978-94-017-8663-8. [Google Scholar]
- Appiah Mensah, A.; Jonzén, J.; Nyström, K.; Wallerman, J.; Nilsson, M. Mapping site index in coniferous forests using bi-temporal airborne laser scanning data and field data from the Swedish national forest inventory. For. Ecol. Manag. 2023, 547, 121395. [Google Scholar] [CrossRef]
- Elamin, A.; Abdelaziz, N.; El-Rabbany, A. A GNSS/INS/LiDAR Integration Scheme for UAV-Based Navigation in GNSS-Challenging Environments. Sensors 2022, 22, 9908. [Google Scholar] [CrossRef]
- Loghin, A.; Oniga, E.; Wieser, M. Analysing and Modelling Terrain Surface Changes using Airborne Laser Scanning Data. World J. Eng. Res. Technol. 2016, 2, 87–95. [Google Scholar]
- Torresan, C.; Berton, A.; Carotenuto, F.; Chiavetta, U.; Miglietta, F.; Zaldei, A.; Gioli, B. Development and Performance Assessment of a Low-Cost UAV Laser Scanner System (LasUAV). Remote Sens. 2018, 10, 1094. [Google Scholar] [CrossRef]
- Maune, D.F.; Kopp, S.M.; Crawford, C.A.; Zervas, C.E. Introduction. In Digital Elevation Model Technologies and Applications: The DEM Users Manual, 2nd ed.; Maune, D.F., Ed.; American Society for Photogrammetry and Remote Sensing; Bethesda: Rockville, MD, USA, 2007; pp. 9–16. [Google Scholar]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian Decomposition and Calibration of a Novel Small-Footprint Full-Waveform Digitising Airborne Laser Scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Ruiz, L.A.; Hermosilla, T.; Mauro, F.; Godino, M. Analysis of the Influence of Plot Size and LiDAR Density on Forest Structure Attribute Estimates. Forests 2014, 5, 936–951. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, B.; Devereux, B. State-of-the-Art: DTM Generation Using Airborne LIDAR Data. Sensors 2017, 17, 150. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, V. Automated ground filtering of LiDAR and UAS point clouds with metaheuristics. Opt. Laser Technol. 2021, 138, 106890. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. Advanced DTM generation from LIDAR data. Int. Arch. Photogramm. Remote Sens. 2001, 34, 23–30. [Google Scholar]
- Pfeifer, N.; Stadler, P.; Briese, C. Derivation of Digital Terrain Models in the SCOP ++ Environment. In Proceedings of the OEEPE Workshop on Airborne Laser Scanning and Interferometric SAR for Detailed Digital Elevation Models, Stockholm, Sweden, 1–3 March 2001. [Google Scholar]
- Axelsson, P. DEM generation form laser scanner data using adaptive TIN models. Int. Arch. Photogramm. Remote Sens. 2000, 4, 110–118. [Google Scholar]
- Nardinocchi, C.; Forlani, G.; Zingaretti, P. Classification and filtering of laser data. Int. Arch. Photogramm. Remote Sens. 2003, 34. Available online: https://www.isprs.org/proceedings/XXXIV/3-W13/papers/Nardinocchi_ALSDD2003.PDF (accessed on 20 October 2023).
- Jacobsen, K.; Lohmann, P. Segmented filtering of laser scanner DSMs. Int. Arch. Photogramm. Remote Sens 2003, 34. Available online: https://www.isprs.org/proceedings/XXXIV/3-W13/papers/Jacobsen_ALSDD2003.pdf (accessed on 10 October 2023).
- Serifoglu, Y.C.; Gungor, O. Comparison of the performances of ground filtering algorithms and DTM generation from a UAV-based point cloud. Geocarto Int. 2018, 33, 522–537. [Google Scholar] [CrossRef]
- Salach, A.; Bakuła, K.; Pilarska, M.; Ostrowski, W.; Górski, K.; Kurczyński, Z. Accuracy Assessment of Point Clouds from LiDAR and Dense Image Matching Acquired Using the UAV Platform for DTM Creation. ISPRS Int. J. Geo-Inf. 2018, 7, 342. [Google Scholar] [CrossRef]
- Fuad, N.A.; Ismail, Z.; Majid, Z.; Darwin, N.; Ariff, M.F.M.; Idris, K.M.; Yusoff, A.R. Accuracy evaluation of digital terrain model based on different flying altitudes and conditional of terrain using UAV LiDAR technology. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Kuala Lumpur, Malaysia, 24–25 April 2018; IOP Publishing: Bristol, UK, 2018; Volume 169, p. 012100. [Google Scholar]
- Štroner, M.; Urban, R.; Křemen, T.; Braun, J. UAV DTM acquisition in a forested area–comparison of low-cost photogrammetry (DJI Zenmuse P1) and LiDAR solutions (DJI Zenmuse L1). Eur. J. Remote Sens. 2023, 56, 2179942. [Google Scholar] [CrossRef]
- Chen, C.; Guo, J.; Wu, H.; Li, Y.; Shi, B. Performance Comparison of Filtering Algorithms for High-Density Airborne LiDAR Point Clouds over Complex LandScapes. Remote Sens. 2021, 13, 2663. [Google Scholar] [CrossRef]
- Romanian Position Determination System: Real Time Products. Available online: https://www.unoosa.org/documents/pdf/psa/activities/2010/moldova/presentations/3-3.pdf (accessed on 20 October 2023).
- Oniga, V.E.; Morelli, L.; Macovei, M.; Chirila, C.; Breaban, A.I.; Remondino, F.; Sestraș, P. PPK Processing to Boost Accuracy in Cadastral Mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 48, 345–352. [Google Scholar] [CrossRef]
- Dreier, A.; Janßen, J.; Kuhlmann, H.; Klingbeil, L. Quality Analysis of Direct Georeferencing in Aspects of Absolute Accuracy and Precision for a UAV-Based Laser Scanning System. Remote Sens. 2021, 13, 3564. [Google Scholar] [CrossRef]
- Shuttle V5.7 User Guide. Available online: https://fshop.oss-accelerate.aliyuncs.com/20200611113453747081734.pdf (accessed on 1 November 2023).
- Help TransDatRO: User Guide; National Agency for Cadastre and Land Registration; National Center for Cartography: Bucharest, Romania, 2022; Available online: https://cngcft.ro/index.php/ro/ (accessed on 20 October 2023).
- OPALS Orientation and Processing of Airborne Laser Scanning Data. Available online: http://geo.tuwien.ac.at/opals/html/ModuleGrid.html (accessed on 1 November 2023).
- Pfeifer, N.; Mandlburger, G.; Otepka, J.; Karel, W. OPALS—A framework for Airborne Laser Scanning data analysis. Comput. Environ. Urban Syst. 2014, 45, 125–136. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Línková, L. A New Method for UAV Lidar Precision Testing Used for the Evaluation of an Affordable DJI ZENMUSE L1 Scanner. Remote Sens. 2021, 13, 4811. [Google Scholar] [CrossRef]
- CloudCompare OfficialWeb Site. Available online: http://www.danielgm.net/cc/ (accessed on 1 November 2023).
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Piltz, B.; Bayer, S.; Poznanska, A.M. Volume based DTM generation from very high resolution photogrammetric DSMs. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, 41, 83–90. [Google Scholar] [CrossRef]
- Pfeifer, N.; Mandlburger, G. Filtering and DTM Generation. In Topographic Laser Ranging and Scanning: Principles and Processing; Shan, J., Toth, C., Eds.; CRC Press: Boca Raton, FL, USA, 2008; pp. 307–333. ISBN 9781420051421. [Google Scholar]
- Štroner, M.; Urban, R.; Lidmila, M.; Kolár, V.; Kremen, T. Vegetation Filtering of a Steep Rugged Terrain: The Performance of Standard Algorithms and a Newly Proposed Workflow on an Example of a Railway Ledge. Remote Sens. 2021, 13, 3050. [Google Scholar] [CrossRef]
- Kuçak, R.A.; Büyüksalih, İ. Comparison of CSF Ground Filtering Method by Using Airborne LiDAR Data. Adv. LiDAR 2023, 3, 47–52. [Google Scholar]
- Sarıtaş, B.; Kaplan, G. Enhancing Ground Point Extraction in Airborne LiDAR Point Cloud Data Using the CSF Filter Algorithm. Adv. LiDAR 2023, 3, 53–61. [Google Scholar]
- Hollaus, M.; Mandlburger, G.; Pfeifer, N.; Mücke, W. Land Cover Dependent Derivation of Digital Surface models from Airborne Laser Scanning Data. IAPRS 2010, 38, 221–226. [Google Scholar]





















| LiDAR-UAS Point Cloud | No. of Points | Density Points/sqm |
|---|---|---|
| 60 m height | 39,287,325 | 564 |
| 100 m height | 20,159,785 | 300 |
| LiDAR-UAS Point Cloud | RMSEX σ (cm) | RMSEY σ (cm) | RMSEZ σ (cm) | RMSEX,Y σ (cm) | RMSETOT σ (cm) |
|---|---|---|---|---|---|
| 60 m height | 3.3 3.3 | 3.5 2.9 | 2.2 1.4 | 4.8 2.0 | 5.3 2.0 |
| 100 m height | 5.0 4.9 | 4.2 3.7 | 3.7 2.2 | 6.5 3.0 | 7.5 2.8 |
| LiDAR-UAS Point Cloud | RMSEX (cm) | RMSEY (cm) | RMSEZ (cm) | RMSEX,Y (cm) | RMSETOT (cm) |
|---|---|---|---|---|---|
| 60 m height | 6 | 8 | 7.6 | 10 | 12.6 |
| 100 m height | 8.2 | 11.4 | 11 | 14.1 | 17.9 |
| No. of LiDAR-UAS Ground Points | 60 m Heigh | 100 m Height |
|---|---|---|
| Hierarchic robust | 17,814,702 | 11,092,862 |
| Morphological volume-based (steep slopes only) | 175,641 | 88,681 |
| Total (combined) | 17,990,343 | 11,181,543 |
| No. of Ground Points | CSF | Volume-Based Filter | Volume-Based Morphological Filter | Hierarchic Robust Filter | Proposed Method |
|---|---|---|---|---|---|
| 60 m height | 19,844,316 | 16,611,900 | 15,300,117 | 17,990,702 | 17,990,343 |
| 100 m height | 11,713,850 | 10,016,332 | 9,071,908 | 11,092,862 | 11,181,543 |
| Filtering Method | Accuracy Metrics (m) | |||
|---|---|---|---|---|
| µ | Median | σ | RMSE | |
| CSF | ||||
| 60 m | −0.04 | 0.01 | 0.29 | 0.29 |
| 100 m | −0.05 | −0.01 | 0.28 | 0.29 |
| Volume-based morphological filter | ||||
| 60 m | 0.01 | 0.00 | 0.28 | 0.28 |
| 100 m | −0.01 | −0.02 | 0.29 | 0.29 |
| Hierarchic robust filter | ||||
| 60 m | −0.02 | 0.01 | 0.25 | 0.25 |
| 100 m | −0.04 | −0.01 | 0.25 | 0.25 |
| Proposed method | ||||
| 60 m | −0.00 | 0.01 | 0.16 | 0.15 |
| 100 m | −0.02 | −0.01 | 0.18 | 0.18 |
| CSF | Volume-Based Morphological Filter | Hierarchic Robust Filter | Proposed Method |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
| |||
|
|
|
|
|
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oniga, V.-E.; Loghin, A.-M.; Macovei, M.; Lazar, A.-A.; Boroianu, B.; Sestras, P. Enhancing LiDAR-UAS Derived Digital Terrain Models with Hierarchic Robust and Volume-Based Filtering Approaches for Precision Topographic Mapping. Remote Sens. 2024, 16, 78. https://doi.org/10.3390/rs16010078
Oniga V-E, Loghin A-M, Macovei M, Lazar A-A, Boroianu B, Sestras P. Enhancing LiDAR-UAS Derived Digital Terrain Models with Hierarchic Robust and Volume-Based Filtering Approaches for Precision Topographic Mapping. Remote Sensing. 2024; 16(1):78. https://doi.org/10.3390/rs16010078
Chicago/Turabian StyleOniga, Valeria-Ersilia, Ana-Maria Loghin, Mihaela Macovei, Anca-Alina Lazar, Bogdan Boroianu, and Paul Sestras. 2024. "Enhancing LiDAR-UAS Derived Digital Terrain Models with Hierarchic Robust and Volume-Based Filtering Approaches for Precision Topographic Mapping" Remote Sensing 16, no. 1: 78. https://doi.org/10.3390/rs16010078
APA StyleOniga, V. -E., Loghin, A. -M., Macovei, M., Lazar, A. -A., Boroianu, B., & Sestras, P. (2024). Enhancing LiDAR-UAS Derived Digital Terrain Models with Hierarchic Robust and Volume-Based Filtering Approaches for Precision Topographic Mapping. Remote Sensing, 16(1), 78. https://doi.org/10.3390/rs16010078