Dynamic Spatial–Spectral Feature Optimization-Based Point Cloud Classification
Abstract
:1. Introduction
2. Materials and Methods
2.1. Datasets
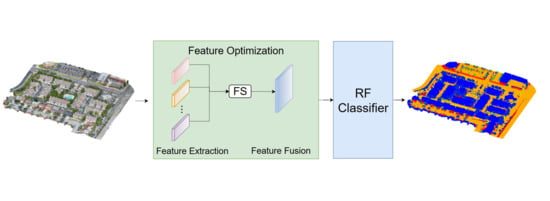
2.2. The Proposed Method
2.2.1. Voxel Preprocessing
| Algorithm 1 Large-scale point cloud classification using random forest based on weighted feature spatial transformation |
Input: : Point cloud dataset
|
2.2.2. Feature Extraction Based on Statistical Analysis and Spatial–Spectral Information
- Comparative features of spectral information
- Spatial information distribution features
- Global features
- Localized spatial enhancement features
- Elevation features and plane roughness
2.2.3. Feature Selection and Feature Fusion
- Feature selection based on feature importance and correlation
- Multi-features weighted fusion
2.2.4. Classification with RF
2.2.5. Evaluation Index
3. Results
3.1. Classification Accuracy
3.2. Classification Results
3.3. Comparison with Other Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Höfle, B.; Hollaus, M.; Hagenauer, J. Urban vegetation detection using radiometrically calibrated small-footprint full-waveform airborne LiDAR data. Isprs J. Photogramm. Remote Sens. 2012, 67, 134–147. [Google Scholar] [CrossRef]
- Chen, T.W.; Lu, M.H.; Yan, W.Z.; Fan, Y.C. 3D LiDAR Automatic Driving Environment Detection System Based on MobileNetv3-YOLOv4. In Proceedings of the 2022 IEEE International Conference on Consumer Electronics (ICCE), Taipei, Taiwan, 6–8 July 2022; pp. 1–2. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Gao, S.; Wu, F.; Guo, Q. Separating the Structural Components of Maize for Field Phenotyping Using Terrestrial LiDAR Data and Deep Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2644–2658. [Google Scholar] [CrossRef]
- Zhou, X.; Li, W. A Geographic Object-Based Approach for Land Classification Using LiDAR Elevation and Intensity. IEEE Geosci. Remote Sens. Lett. 2017, 14, 669–673. [Google Scholar] [CrossRef]
- Tan, S.; Stoker, J.; Greenlee, S. Detection of foliage-obscured vehicle using a multiwavelength polarimetric lidar. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 2503–2506. [Google Scholar] [CrossRef]
- Barnefske, E.; Sternberg, H. Evaluation of Class Distribution and Class Combinations on Semantic Segmentation of 3D Point Clouds With PointNet. IEEE Access 2023, 11, 3826–3845. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Y.; Zhang, S.; Ogai, H. Deep 3D Object Detection Networks Using LiDAR Data: A Review. IEEE Sens. J. 2021, 21, 1152–1171. [Google Scholar] [CrossRef]
- Guiotte, F.; Pham, M.T.; Dambreville, R.; Corpetti, T.; Lefvre, S. Semantic Segmentation of LiDAR Points Clouds: Rasterization Beyond Digital Elevation Models. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2016–2019. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11105–11114. [Google Scholar] [CrossRef]
- Lin, X.; Xie, W. A segment-based filtering method for mobile laser scanning point cloud. Int. J. Image Data Fusion 2022, 13, 136–154. [Google Scholar] [CrossRef]
- Wei, X.; Yu, R.; Sun, J. View-GCN: View-Based Graph Convolutional Network for 3D Shape Analysis. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1847–1856. [Google Scholar] [CrossRef]
- Milioto, A.; Vizzo, I.; Behley, J.; Stachniss, C. Rangenet++: Fast and accurate lidar semantic segmentation. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4213–4220. [Google Scholar] [CrossRef]
- Tatarchenko, M.; Park, J.; Koltun, V.; Zhou, Q.Y. Tangent convolutions for dense prediction in 3d. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3887–3896. [Google Scholar] [CrossRef]
- Wu, B.; Zhou, X.; Zhao, S.; Yue, X.; Keutzer, K. Squeezesegv2: Improved model structure and unsupervised domain adaptation for road-object segmentation from a lidar point cloud. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4376–4382. [Google Scholar] [CrossRef]
- Maturana, D.; Scherer, S. VoxNet: A 3D Convolutional Neural Network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September 2015–2 October 2015; pp. 922–928. [Google Scholar] [CrossRef]
- Riegler, G.; Osman Ulusoy, A.; Geiger, A. Octnet: Learning deep 3d representations at high resolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3577–3586. [Google Scholar] [CrossRef]
- Chen, X.; Ma, H.; Wan, J.; Li, B.; Xia, T. Multi-view 3d object detection network for autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1907–1915. [Google Scholar] [CrossRef]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- He, P.; Gao, K.; Liu, W.; Song, W.; Hu, Q.; Cheng, X.; Li, S. OFFS-Net: Optimal Feature Fusion-Based Spectral Information Network for Airborne Point Cloud Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 141–152. [Google Scholar] [CrossRef]
- Zhao, C.; Yu, D.; Xu, J.; Zhang, B.; Li, D. Airborne LiDAR point cloud classification based on transfer learning. In Proceedings of the International Conference on Digital Image Processing, Guangzhou, China, 10–13 May 2019. [Google Scholar]
- Poliyapram, V.; Wang, W.; Nakamura, R. A Point-Wise LiDAR and Image Multimodal Fusion Network (PMNet) for Aerial Point Cloud 3D Semantic Segmentation. Remote Sens. 2019, 11, 2961. [Google Scholar] [CrossRef]
- Li, D.; Shen, X.; Guan, H.; Yu, Y.; Wang, H.; Zhang, G.; Li, J.; Li, D. AGFP-Net: Attentive geometric feature pyramid network for land cover classification using airborne multispectral LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102723. [Google Scholar] [CrossRef]
- Xiu, H.; Vinayaraj, P.; Kim, K.S.; Nakamura, R.; Yan, W. 3D Semantic Segmentation for High-Resolution Aerial Survey Derived Point Clouds Using Deep Learning (Demonstration). In Proceedings of the 26th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, New York, NY, USA, 6 November 2018; SIGSPATIAL ’18. pp. 588–591. [Google Scholar] [CrossRef]
- Aljumaily, H.; Laefer, D.F.; Cuadra, D.; Velasco, M. Point cloud voxel classification of aerial urban LiDAR using voxel attributes and random forest approach. Int. J. Appl. Earth Obs. Geoinform. 2023, 118, 103208. [Google Scholar] [CrossRef]
- Chehata, N.; Guo, L.; Mallet, C. Airborne lidar feature selection for urban classification using random forests. In Proceedings of the Laserscanning, Paris, France, 1–2 September 2009. [Google Scholar]
- Farnaaz, N.; Jabbar, M. Random Forest Modeling for Network Intrusion Detection System. Procedia Comput. Sci. 2016, 89, 213–217. [Google Scholar] [CrossRef]
- Chen, M.; Hu, Q.; Hugues, T.; Feng, A.; Hou, Y.; McCullough, K.; Soibelman, L. STPLS3D: A large-scale synthetic and real aerial photogrammetry 3D point cloud dataset. arXiv 2022, arXiv:2203.09065. [Google Scholar] [CrossRef]
- Lepetit, V.; Fua, P. Keypoint recognition using randomized trees. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1465–1479. [Google Scholar] [CrossRef]
- Shotton, J.; Glocker, B.; Zach, C.; Izadi, S.; Criminisi, A.; Fitzgibbon, A. Scene Coordinate Regression Forests for Camera Relocalization in RGB-D Images. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2930–2937. [Google Scholar] [CrossRef]
- Guo, L.; Chehata, N.; Mallet, C.; Boukir, S. Relevance of airborne lidar and multispectral image data for urban scene classification using Random Forests. ISPRS J. Photogramm. Remote Sens. 2011, 66, 56–66. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 27–31 August 1998; AAAI Press: Portland, Oregon, 1996; pp. 226–231. [Google Scholar]
- Deng, D. DBSCAN Clustering Algorithm Based on Density. In Proceedings of the 2020 7th International Forum on Electrical Engineering and Automation (IFEEA), Hefei, China, 25–27 September 2020; pp. 949–953. [Google Scholar] [CrossRef]
- Louhichi, S.; Gzara, M.; Ben Abdallah, H. A density based algorithm for discovering clusters with varied density. In Proceedings of the 2014 World Congress on Computer Applications and Information Systems (WCCAIS), Hammamet, Tunisia, 17–19 January 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Gu, Q.; Li, Z.; Han, J. Generalized Fisher Score for Feature Selection. In Proceedings of the Twenty-Seventh Conference on Uncertainty in Artificial Intelligence, Arlington, VG, USA, 14–17 July 2011; pp. 266–273. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef]
- Yang, Y.; Pedersen, J.O. A Comparative Study on Feature Selection in Text Categorization. In Proceedings of the International Conference on Machine Learning, Nashville, TN, USA, 8–12 July 1997. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Kim, T.; Park, S.; Lee, K.T. Depth-Aware Feature Pyramid Network for Semantic Segmentation. In Proceedings of the 2023 Fourteenth International Conference on Ubiquitous and Future Networks (ICUFN), Paris, France, 4–7 July 2023; pp. 487–490. [Google Scholar] [CrossRef]
- Zhu, L.; Huang, J.; Ye, S. Unsupervised Semantic Segmentation with Feature Fusion. In Proceedings of the 2023 3rd Asia-Pacific Conference on Communications Technology and Computer Science (ACCTCS), Shenyang, China, 25–27 February 2023; pp. 162–167. [Google Scholar] [CrossRef]
- Zhao, W.; Kang, Y.; Chen, H.; Zhao, Z.; Zhao, Z.; Zhai, Y. Adaptively Attentional Feature Fusion Oriented to Multiscale Object Detection in Remote Sensing Images. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Dai, Y.; Gieseke, F.; Oehmcke, S.; Wu, Y.; Barnard, K. Attentional Feature Fusion. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2021; pp. 3559–3568. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhou, Z.; Feng, J. Deep forest. Natl. Sci. Rev. 2018, 6, 74–86. [Google Scholar] [CrossRef] [PubMed]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF international conference on computer vision, Montreal, BC, Canada, 11–17 October 2021; pp. 16259–16268. [Google Scholar] [CrossRef]
- Fan, S.; Dong, Q.; Zhu, F.; Lv, Y.; Ye, P.; Wang, F.Y. SCF-Net: Learning Spatial Contextual Features for Large-Scale Point Cloud Segmentation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 14499–14508. [Google Scholar] [CrossRef]
- Choy, C.; Gwak, J.; Savarese, S. 4D Spatio-Temporal ConvNets: Minkowski Convolutional Neural Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3070–3079. [Google Scholar] [CrossRef]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L. KPConv: Flexible and Deformable Convolution for Point Clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6410–6419. [Google Scholar] [CrossRef]
















| RA | WMSC | OCCC | USC | |
|---|---|---|---|---|
| Building | 2,388,323 (34.99%) | 996,180 (9.98%) | 14,742,339 (37.88%) | 40,094,389 (42.34%) |
| Low vegetation | 1,460,336 (21.10%) | 2,086,770 (20.91%) | 6,685,428 (17.18%) | 27,996,830 (29.57%) |
| Vehicle | 133,085 (1.95%) | 42,033 (0.42%) | 964,766 (2.48%) | 478,130 (0.50%) |
| Light Pole | 18,870 (0.28%) | 6,232 (0.06%) | 74,233 (0.19%) | 179,555 (0.19%) |
| Clutter | 32,383 (0.47%) | 134,859 (1.35%) | 145,289 (0.37%) | 2,112,812 (2.23%) |
| Fence | 333,862 (4.89%) | 76,296 (0.76%) | 56,405 (0.14%) | 819,305 (0.87%) |
| Road | 2,054,448 (30.10%) | 754,171 (7.56%) | 8,636,482 (22.19%) | 16,051,158 (16.95%) |
| Dirt | 32,315 (0.47%) | 4,700,616 (47.11%) | 1,393,234 (3.58%) | 828,581 (0.88%) |
| Grass | 371,443 (5.44%) | 1,180,607 (11.83%) | 6,216,458 (15.97%) | 6,134,089 (6.48%) |
| Total | 6,825,065 (100%) | 9,977,764 (100%) | 38,914,634 (100%) | 94,694,849 (100%) |
| Method | mIoU (%) | oAcc (%) | Per Class IoU (%) | |||||
|---|---|---|---|---|---|---|---|---|
| Ground | Building | Tree | Car | Light Pole | Fence | |||
| PointTransformer [47] | 36.27 | 54.31 | 39.95 | 20.88 | 62.57 | 36.13 | 49.32 | 8.76 |
| RandLA-Net [9] | 42.33 | 60.19 | 46.13 | 24.23 | 72.46 | 53.37 | 44.82 | 12.95 |
| SCF-Net [48] | 45.93 | 75.75 | 68.77 | 37.27 | 65.49 | 51.5 | 31.22 | 21.34 |
| MinkowskiNet [49] | 46.52 | 70.44 | 64.22 | 29.95 | 61.33 | 45.96 | 65.25 | 12.43 |
| KPConv [50] | 45.22 | 70.67 | 60.87 | 32.13 | 69.05 | 53.8 | 52.08 | 3.4 |
| The proposed method | 84.49 | 96.83 | 95.65 | 96.39 | 88.31 | 83.38 | 78.25 | 64.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Feng, W.; Quan, Y.; Ye, G.; Dauphin, G. Dynamic Spatial–Spectral Feature Optimization-Based Point Cloud Classification. Remote Sens. 2024, 16, 575. https://doi.org/10.3390/rs16030575
Zhang Y, Feng W, Quan Y, Ye G, Dauphin G. Dynamic Spatial–Spectral Feature Optimization-Based Point Cloud Classification. Remote Sensing. 2024; 16(3):575. https://doi.org/10.3390/rs16030575
Chicago/Turabian StyleZhang, Yali, Wei Feng, Yinghui Quan, Guangqiang Ye, and Gabriel Dauphin. 2024. "Dynamic Spatial–Spectral Feature Optimization-Based Point Cloud Classification" Remote Sensing 16, no. 3: 575. https://doi.org/10.3390/rs16030575
APA StyleZhang, Y., Feng, W., Quan, Y., Ye, G., & Dauphin, G. (2024). Dynamic Spatial–Spectral Feature Optimization-Based Point Cloud Classification. Remote Sensing, 16(3), 575. https://doi.org/10.3390/rs16030575