Radar High-Resolution Range Profile Rejection Based on Deep Multi-Modal Support Vector Data Description
Abstract
:1. Introduction
- An efficient rejection method for HRRP is proposed, which jointly optimizes feature extraction and rejection boundary learning under a unified distance-based criterion;
- The dual attention module in the feature extractor is capable of capturing the global and local structure information of HRRP, which further strengthens the feature discrimination between the in-library and out-of-library samples.
- Considering the high-dimensional and multi-modal structure of HRRP, a more compact and explicit rejection boundary is formed with an adjustable GMM;
- A semi-supervised method is extended to take advantage of available out-of-library samples to assist rejection boundary learning;
- Experiments demonstrate that the proposed methods can significantly promote the rejection performance on the measured HRRP dataset.
2. Related Work
2.1. Support Vector Data Description
2.2. Deep Support Vector Data Description
2.3. Deep Multi-Sphere Support Vector Data Description
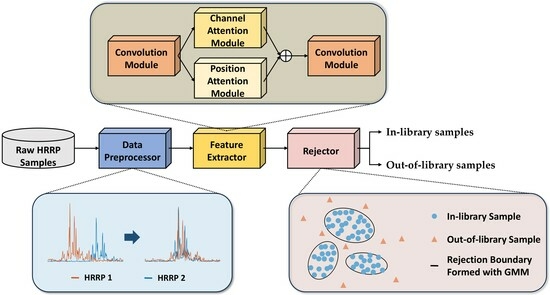
3. The Proposed Method
3.1. Data Preprocessor
3.2. Feature Extractor
3.3. Rejector
3.4. Objective Function
3.5. Training
3.5.1. Initializing
- Initialization of feature extractor
- Initialization of GMM
3.5.2. Updating
3.6. Theoretical Analysis
3.7. Rejection Criterion
4. Results
4.1. Dataset
4.2. Implementation Details
4.3. Evaluation Metrics
4.4. Experiment with All Training Samples
4.5. Experiment with Different Training Sample Sizes
5. Discussion
5.1. Ablation Study
5.2. Visualization
5.2.1. Visualization of Separability
5.2.2. Visualization of Position Attention Maps
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, T.; Zhang, X.; Liu, C.; Shi, J.; Wei, S.; Ahmad, I.; Zhan, X.; Zhou, Y.; Pan, D.; Li, J. Balance learning for ship detection from synthetic aperture radar remote sensing imagery. ISPRS J. Photogramm. 2021, 182, 190–207. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. A mask attention interaction and scale enhancement network for SAR ship instance segmentation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4511005. [Google Scholar] [CrossRef]
- Yan, J.; Jiao, H.; Pu, W.; Shi, C.; Dai, J.; Liu, H. Radar sensor network resource allocation for fused target tracking: A brief review. Inform. Fusion 2022, 86, 104–115. [Google Scholar] [CrossRef]
- Yan, J.; Pu, W.; Zhou, S.; Liu, H.; Bao, Z. Collaborative detection and power allocation framework for target tracking in multiple radar system. Inform. Fusion 2020, 55, 173–183. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, J.; Liu, H.; Ho, K.; Chen, Y.; Yang, Z. Optimal sensor placement for source tracking under synchronization offsets and sensor location errors with distance-dependent noises. Signal Process. 2022, 193, 108399. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Bai, X. End-to-end radar HRRP target recognition based on integrated denoising and recognition network. Remote Sens. 2022, 14, 5254. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. A polarization fusion network with geometric feature embedding for SAR ship classification. Pattern Recogn. 2022, 123, 108365. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. Squeeze-and-excitation Laplacian pyramid network with dual-polarization feature fusion for ship classification in SAR images. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4019905. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. Injection of traditional hand-crafted features into modern CNN-based models for SAR ship classification: What, why, where, and how. Remote Sens. 2021, 13, 2091. [Google Scholar] [CrossRef]
- Li, X.; Ran, J.; Wen, Y.; Wei, S.; Yang, W. MVFRnet: A novel high-accuracy network for ISAR air-target recognition via multi-view fusion. Remote Sens. 2023, 15, 3052. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef]
- Tax, D.M.; Duin, R.P. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation forest. In Proceedings of the Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008. [Google Scholar]
- Erfani, S.M.; Rajasegarar, S.; Karunasekera, S.; Leckie, C. High-dimensional and large-scale anomaly detection using a linear one-class SVM with deep learning. Pattern Recogn. 2016, 58, 121–134. [Google Scholar] [CrossRef]
- Andrews, J.; Tanay, T.; Morton, E.J.; Griffin, L.D. Transfer representation-learning for anomaly detection. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016. [Google Scholar]
- Pang, G.; Shen, C.; Cao, L.; Hengel, A.V.D. Deep learning for anomaly detection: A review. ACM Comput. Surv. 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Perera, P.; Nallapati, R.; Xiang, B. OCGAN: One-class novelty detection using GANs with constrained latent representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. GANomaly: Semi-supervised anomaly detection via adversarial training. In Proceedings of the 14th Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2019. [Google Scholar]
- Zaheer, M.Z.; Lee, J.-h.; Astrid, M.; Lee, S.-I. Old is gold: Redefining the adversarially learned one-class classifier training paradigm. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Sabokrou, M.; Fathy, M.; Zhao, G.; Adeli, E. Deep end-to-end one-class classifier. IEEE Trans. Neur. Net. Lear. 2020, 32, 675–684. [Google Scholar] [CrossRef]
- Golan, I.; El-Yaniv, R. Deep anomaly detection using geometric transformations. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Tack, J.; Mo, S.; Jeong, J.; Shin, J. CSI: Novelty detection via contrastive learning on distributionally shifted instances. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020. [Google Scholar]
- Ristea, N.-C.; Madan, N.; Ionescu, R.T.; Nasrollahi, K.; Khan, F.S.; Moeslund, T.B.; Shah, M. Self-supervised predictive convolutional attentive block for anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Ruff, L.; Vandermeulen, R.; Goernitz, N.; Deecke, L.; Siddiqui, S.A.; Binder, A.; Müller, E.; Kloft, M. Deep one-class classification. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Ghafoori, Z.; Leckie, C. Deep multi-sphere support vector data description. In Proceedings of the 2020 SIAM International Conference on Data Mining, Cincinnati, OH, USA, 7–9 May 2020. [Google Scholar]
- Xia, Z.; Wang, P.; Dong, G.; Liu, H.J. Radar HRRP Open Set Recognition Based on Extreme Value Distribution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3257879. [Google Scholar] [CrossRef]
- Chen, J.; Du, L.; Guo, G.; Yin, L.; Wei, D. Target-attentional CNN for radar automatic target recognition with HRRP. Signal Process 2022, 196, 108497. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Shi, J.; Wei, S. HyperLi-Net: A hyper-light deep learning network for high-accurate and high-speed ship detection from synthetic aperture radar imagery. ISPRS J. Photogramm. 2020, 167, 123–153. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Ke, X. Quad-FPN: A novel quad feature pyramid network for SAR ship detection. Remote Sens. 2021, 13, 2771. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. A full-level context squeeze-and-excitation ROI extractor for SAR ship instance segmentation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4506705. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Ke, X.; Liu, C.; Xu, X.; Zhan, X.; Wang, C.; Ahmad, I.; Zhou, Y.; Pan, D. HOG-ShipCLSNet: A novel deep learning network with hog feature fusion for SAR ship classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–22. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Wang, P.; Shi, L.; Du, L.; Liu, H.; Xu, L.; Bao, Z. Radar HRRP statistical recognition with temporal factor analysis by automatic Bayesian Ying-Yang harmony learning. Front. Electr. Electron. Eng. China 2011, 6, 300–317. [Google Scholar] [CrossRef]
- Liu, H.; Du, L.; Wang, P.; Pan, M.; Bao, Z. Radar HRRP automatic target recognition: Algorithms and applications. In Proceedings of the 2011 IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011. [Google Scholar]
- Hendrycks, D.; Mazeika, M.; Dietterich, T. Deep anomaly detection with outlier exposure. arXiv 2018, arXiv:1812.04606. [Google Scholar]
- Ruff, L.; Vandermeulen, R.A.; Görnitz, N.; Binder, A.; Müller, E.; Müller, K.-R.; Kloft, M. Deep semi-supervised anomaly detection. arXiv 2019, arXiv:1906.02694. [Google Scholar]
- Yao, X.; Li, R.; Zhang, J.; Sun, J.; Zhang, C. Explicit Boundary Guided Semi-Push-Pull Contrastive Learning for Supervised Anomaly Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 24490–24499. [Google Scholar]
- Zaheer, M.Z.; Mahmood, A.; Khan, M.H.; Segu, M.; Yu, F.; Lee, S.-I. Generative cooperative learning for unsupervised video anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Caliafornia, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966. [Google Scholar]
- Ball, G.H.; Hall, D.J. A clustering technique for summarizing multivariate data. Behav. Sci. 1967, 12, 153–155. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.-S.; Lai, C.-Y.; Lin, C.-Y. A robust EM clustering algorithm for Gaussian mixture models. Pattern Recogn. 2012, 45, 3950–3961. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Pernkopf, F.; Bouchaffra, D. Genetic-based EM algorithm for learning Gaussian mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1344–1348. [Google Scholar] [CrossRef] [PubMed]
- Masci, J.; Meier, U.; Cireşan, D.; Schmidhuber, J. Stacked convolutional auto-encoders for hierarchical feature extraction. In Proceedings of the 21st International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Lv, H.; Chen, C.; Cui, Z.; Xu, C.; Li, Y.; Yang, J. Learning normal dynamics in videos with meta prototype network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Hu, W.; Wang, M.; Qin, Q.; Ma, J.; Liu, B. HRN: A holistic approach to one class learning. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020. [Google Scholar]
- Qiu, C.; Pfrommer, T.; Kloft, M.; Mandt, S.; Rudolph, M. Neural transformation learning for deep anomaly detection beyond images. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing non-metric similarities in multiple maps. Mach. Learn. 2012, 87, 33–55. [Google Scholar] [CrossRef]









| Module | Layer | Output Size | Normalization/Activation | |
|---|---|---|---|---|
| Feature Extractor | Convolution Module 1 | Conv1D | 8 × 256 | BN/Leaky ReLU |
| Max Pooling | 8 × 128 | - | ||
| Conv1D | 16 × 128 | BN/Leaky ReLU | ||
| Max Pooling | 16 × 64 | - | ||
| Dual Attention Module | Channel Attention | 16 × 64 | - | |
| Position Attention | 16 × 64 | - | ||
| Convolution Module 2 | Conv1D | 8 × 64 | BN/Leaky ReLU | |
| Max Pooling | 8 × 32 | - | ||
| Flattening | 1 × 256 | - | ||
| Conv1D | 1 × 32 | - | ||
| Decoder | Deconvolution Module 1 | Reshape | 2 × 16 | - |
| Upsample | 2 × 32 | - | ||
| Deconv1D | 8 × 32 | BN/Leaky ReLU | ||
| Upsample | 8 × 64 | - | ||
| Deconv1D | 16 × 64 | BN/Leaky ReLU | ||
| Upsample | 16 × 128 | - | ||
| Dual Attention Module | Channel Attention | 16 × 128 | - | |
| Position Attention | 16 × 128 | - | ||
| Deconvolution Module 2 | Deconv1D | 8 × 128 | BN/Leaky ReLU | |
| Upsample | 8 × 256 | - | ||
| Deconv1D | 1 × 256 | BN/Leaky ReLU | ||
| Sigmoid | 1 × 256 | - |
| Method | AUC/F1-Score | ||||
|---|---|---|---|---|---|
| Setting I | Setting II | Setting III | Setting IV | Average | |
| OCSVM | 50.80/41.07 | 83.98/73.52 | 59.03/46.38 | 61.88/50.46 | 63.92/52.86 |
| IF | 52.62/43.31 | 80.58/63.59 | 54.91/45.22 | 51.82/42.66 | 59.98/48.70 |
| KDE | 47.06/38.10 | 81.88/69.66 | 53.91/41.40 | 55.67/45.38 | 59.63/48.64 |
| AE | 52.06/42.25 | 64.55/53.19 | 54.56/43.93 | 68.02/54.93 | 59.80/48.58 |
| VAE | 48.30/39.09 | 67.62/56.70 | 48.28/38.95 | 48.40/37.76 | 53.15/43.13 |
| MPN | 64.15/53.23 | 78.64/67.01 | 59.58/47.64 | 70.16/57.05 | 68.13/56.23 |
| HRN | 56.55/46.09 | 68.87/57.64 | 54.60/44.64 | 59.43/49.13 | 59.86/49.38 |
| NeuTraLAD | 62.96/51.18 | 81.55/68.28 | 56.25/45.45 | 65.60/53.39 | 66.59/54.58 |
| DSVDD | 62.82/51.08 | 82.07/69.46 | 67.32/55.10 | 66.69/54.76 | 69.73/57.60 |
| DMSVDD | 66.07/53.98 | 86.77/74.81 | 67.79/55.63 | 67.01/55.23 | 71.91/59.91 |
| DMMSVDD (ours) | 74.77/62.46 | 90.64/79.57 | 80.79/68.25 | 69.04/56.19 | 78.81/66.61 |
| DMMSAD (ours) | 75.41/62.39 | 91.16/81.09 | 81.01/68.50 | 76.03/64.00 | 80.90/68.99 |
| Method | Training Sample Sizes (AUC/F1-Score) | |||
|---|---|---|---|---|
| 3750 | 7500 | 15,000 | 30,000 | |
| OCSVM | 79.54/73.93 | 79.59/73.76 | 79.63/74.01 | 79.67/77.46 |
| IF | 75.91/71.32 | 76.07/71.41 | 76.15/71.45 | 76.18/71.54 |
| KDE | 75.50/71.72 | 75.79/71.98 | 75.80/72.01 | 75.83/73.76 |
| AE | 73.93/67.96 | 77.46/70.44 | 78.19/70.79 | 79.01/70.54 |
| VAE | 64.83/61.54 | 64.91/61.57 | 64.95/61.62 | 65.13/61.85 |
| MPN | 68.75/63.84 | 73.26/66.83 | 78.40/71.49 | 78.77/71.89 |
| HRN | 68.12/62.88 | 71.09/65.41 | 71.44/66.32 | 72.19/66.47 |
| NeuTraLAD | 78.26/71.14 | 78.49/71.58 | 79.01/71.76 | 79.26/71.93 |
| DSVDD | 78.00/71.54 | 78.19/71.68 | 78.85/72.09 | 81.25/74.16 |
| DMSVDD | 78.85/71.84 | 79.86/72.79 | 80.27/73.09 | 83.87/73.77 |
| DMMSVDD (ours) | 83.06/76.06 | 84.97/78.08 | 86.49/79.99 | 87.70/79.88 |
| Method | GMM | Channel Attention | Position Attention | Out-of-Library Samples | AUC |
|---|---|---|---|---|---|
| DMSVDD | 66.07 | ||||
| DMSVDD-GMM | √ | 73.77 | |||
| DMSVDD-GMMCA | √ | √ | 74.22 | ||
| DMMSVDD (ours) | √ | √ | √ | 74.77 | |
| DMMSAD (ours) | √ | √ | √ | √ | 75.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Wang, P.; Fang, M.; Guo, Y.; Cao, L.; Yan, J.; Liu, H. Radar High-Resolution Range Profile Rejection Based on Deep Multi-Modal Support Vector Data Description. Remote Sens. 2024, 16, 649. https://doi.org/10.3390/rs16040649
Dong Y, Wang P, Fang M, Guo Y, Cao L, Yan J, Liu H. Radar High-Resolution Range Profile Rejection Based on Deep Multi-Modal Support Vector Data Description. Remote Sensing. 2024; 16(4):649. https://doi.org/10.3390/rs16040649
Chicago/Turabian StyleDong, Yue, Penghui Wang, Ming Fang, Yifan Guo, Lili Cao, Junkun Yan, and Hongwei Liu. 2024. "Radar High-Resolution Range Profile Rejection Based on Deep Multi-Modal Support Vector Data Description" Remote Sensing 16, no. 4: 649. https://doi.org/10.3390/rs16040649
APA StyleDong, Y., Wang, P., Fang, M., Guo, Y., Cao, L., Yan, J., & Liu, H. (2024). Radar High-Resolution Range Profile Rejection Based on Deep Multi-Modal Support Vector Data Description. Remote Sensing, 16(4), 649. https://doi.org/10.3390/rs16040649