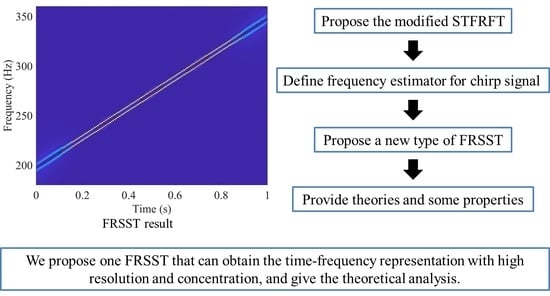
The Synchrosqueezed Method and Its Theory-Analysis-Based Novel Short-Time Fractional Fourier Transform for Chirp Signals
Abstract
:1. Introduction
2. Preliminaries
2.1. Fractional Fourier Transform
2.2. Short-Time FRFT
3. FRSST-Based Novel STFRFT
3.1. Modified Novel STFRFT
3.2. Definition of the New FRSST
3.3. Theoretical Analysis of FRSSTT
3.4. Basic Properties of the FRSST
4. Numerical Examples
4.1. Linear Modulations
4.2. Linear Modulation with Disturbance
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Bracewell, R. The Fourier Transform and Its Applications; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Cooley, J.W.; Lewis, P.A.W.; Welch, P.D. The fast Fourier transform and its applications. IEEE Trans. Educ. 1969, 12, 27–34. [Google Scholar] [CrossRef]
- Namias, V. The fractional order Fourier transform and its application to quantum mechanics. J. Inst. Math. Appl. 1980, 25, 241–265. [Google Scholar] [CrossRef]
- Almeida, L.B. The fractional Fourier transform and time-frequency representations. IEEE Trans. Signal Process. 1994, 42, 3084–3091. [Google Scholar] [CrossRef]
- Cohen, L. Time Frequency Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Gabor, D. Theory of communication. J. Inst. Electr. Eng. 1946, 93, 429–457. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling theory-Part I: Complex signal and scattering in multilayered media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling theory-Part II: Sampling theory and complex waves. Geophysics 1982, 47, 222–236. [Google Scholar] [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy functions into square integrable wavelets of constant shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Gao, J.; Chen, W.; Li, Y.; Tian, F. Generalized S transform and seismic response analysis of thin interbeds. Chin. J. Geophys. 2003, 46, 526–532. [Google Scholar]
- Wignaer, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Ville, J. Theorie et applications de la notion de signal analytique. Cables Trans. 1948, 2A, 61–74. [Google Scholar]
- Mendlovic, D.; Zalevsky, Z.; Lohmann, A.W.; Dorsch, R.G. Signal spatial-filtering using localized fractional Fourier transform. Opt. Commun. 1996, 126, 14–18. [Google Scholar] [CrossRef]
- Zalevsky, Z.; Mendlovic, D.; Caulfield, J.H. Localized, partially space invariant filtering. Appl. Opt. 1997, 36, 1086–1092. [Google Scholar] [CrossRef] [PubMed]
- Ozaktas, H.M.; Kutay, M.A.; Zalevsky, Z. Applications of the fractional Fourier transform to matched filtering, detection, and pattern recognition. In The Fractional Fourier Transform: With Applications Optics and Signal Processing; Wiley: New York, NY, USA, 2000; pp. 455–460. [Google Scholar]
- Mendlovic, D.; Zalevsky, Z.; Mas, D.; García, J.; Ferreira, C. Fractional wavelet transform. Appl. Opt. 1997, 36, 4801–4806. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Liu, X.; Zhang, N. Multiresolution analysis and orthogonal wavelets associated with fractional wavelet transform. Signal Image Video Process. 2015, 9, 211–220. [Google Scholar] [CrossRef]
- Ranjan, R.; Jindal, N.; Singh, A.K. Fractional S-Transform and Its Properties: A Comprehensive Survey. Wirel. Pers. Commun. 2020, 113, 2519–2541. [Google Scholar] [CrossRef]
- Daubechies, I.; Maes, S. A nonlinear squeezing of the continuous wavelet transform based on auditory nerve models. In Wavelets in Medicine and Biology; CRC Press: Boca Raton, FL, USA, 1996; pp. 527–546. [Google Scholar]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed wavelet transform: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P. Improving the readability of time-frequency and time-scale representations by the reassignment method. IEEE Trans. Signal Process. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Thakur, G.; Wu, H.T. Synchrosqueezing-based Recovery of Instantaneous Frequency from Nonuniform Samples. SIAM J. Math. Anal. 2012, 43, 2078–2095. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. The Fourier-based synchrosqueezing transform. In Proceedings of the IEEE International Conference on Acoustics, Florence, Italy, 4–9 May 2014; pp. 315–319. [Google Scholar]
- Huang, Z.; Zhang, J.; Zou, Z. Synchrosqueezing S-transform and its application in seismic spectral decomposition. IEEE Trans. Geosci. Remote Sens. 2016, 54, 817–825. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, J.; Liu, N.; Jiang, X. High-Resolution Seismic Time-Frequency Analysis Using the Synchrosqueezing Generalized S-Transform. IEEE Geosci. Remote Sens. Lett. 2018, 15, 374–378. [Google Scholar] [CrossRef]
- He, D.; Cao, H.; Wang, S.; Chen, X. Time-reassigned synchrosqueezing transform: The algorithm and its applications in mechanical signal processing. Mech. Syst. Signal Process. 2019, 117, 255–279. [Google Scholar] [CrossRef]
- Yu, G. A Concentrated Time-Frequency Analysis Tool for Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2020, 69, 371–381. [Google Scholar] [CrossRef]
- Li, Z.; Gao, J.; Wang, Z. A Time-Synchroextracting Transform for the Time-Frequency Analysis of Seismic Data. IEEE Geosci. Remote Sens. Lett. 2020, 17, 864–868. [Google Scholar] [CrossRef]
- Li, Z.; Gao, J.; Wang, Z.; Liu, N.; Yang, Y. Time-Synchroextracting General Chirplet Transform for Seismic Time-Frequency Analysis. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8626–8636. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. Second-order synchrosqueezing transform or invertible reassignment? Towards ideal time-frequency representations. IEEE Trans. Signal Process. 2015, 63, 1335–1344. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S. The second-order wavelet synchrosqueezing transform. In Proceedings of the IEEE ICASSP, New Orleans, LA, USA, 5–9 May 2017. [Google Scholar]
- Behera, R.; Meignen, S.; Oberlin, T. Theoretical analysis of the second-order synchrosqueezing transform. Appl. Comput. Harmon. Anal. 2016, 34, 1009. [Google Scholar] [CrossRef]
- Han, B.; Zhou, Y.; Yu, G. Second-order synchroextracting wavelet transform for nonstationary signal analysis of rotating machinery. Signal Process. 2021, 186, 108123. [Google Scholar] [CrossRef]
- Yu, G.; Lin, T. Second-order transient-extracting transform for the analysis of impulsive-like signals. Mech. Syst. Signal Process. 2021, 147, 107069. [Google Scholar] [CrossRef]
- Pham, D.; Meignen, S. High-order synchrosqueezing transform for multicomponent signals analysis—With an application to gravitational-wave signal. IEEE Trans. Signal Process. 2017, 65, 3168–3178. [Google Scholar] [CrossRef]
- Lv, S.; Lv, Y.; Yuan, R.; Li, H. High-order synchroextracting transform for characterizing signals with strong AM-FM features and its application in mechanical fault diagnosis. Mech. Syst. Signal Process. 2022, 172, 108959. [Google Scholar] [CrossRef]
- Yu, G.; Yu, M.; Xu, C. Synchroextracting Transform. IEEE Trans. Ind. Electron. 2017, 64, 8042–8054. [Google Scholar] [CrossRef]
- Yu, G.; Wang, Z.; Zhao, P. Multisynchrosqueezing Transform. IEEE Trans. Ind. Electron. 2019, 66, 5441–5455. [Google Scholar] [CrossRef]
- Dong, H.; Yu, G.; Lin, T.; Li, Y. An energy-concentrated wavelet transform for time-frequency analysis of transient signal. Signal Process. 2023, 206, 108934. [Google Scholar] [CrossRef]
- Li, Z.; Gao, J.; Li, H.; Zhang, Z.; Liu, N.; Zhu, X. Synchroextracting transform: The theory analysis and comparisons with the synchrosqueezing transform. Signal Process. 2020, 166, 107243. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Z.; Li, Z.; Gao, J.; Huang, X.; Wen, G. Multiple squeezes from adaptive chirplet transform. Signal Process. 2019, 163, 26–40. [Google Scholar] [CrossRef]
- Yu, G.; Lin, R.; Wang, Z.; Li, Y. Time-Reassigned Multisynchrosqueezing Transform for Bearing Fault Diagnosis of Rotating Machinery. IEEE Trans. Ind. Electron. 2021, 68, 1486–1496. [Google Scholar] [CrossRef]
- Chen, X.; Chen, H.; Hu, Y.; Li, R. A statistical instantaneous frequency estimator for high-concentration time-frequency representation. Signal Process. 2023, 204, 108825. [Google Scholar] [CrossRef]
- Zeyani, A.R. Instantaneous Frequency Estimation and Signal Separation Using Fractional Continuous Wavelet Transform. Ph.D. Dissertation, Univ. Missouri St. Louis, St. Louis, MO, USA, 2021. [Google Scholar]
- Shi, J.; Chen, G.; Zhao, Y.; Tao, R. Synchrosqueezed Fractional Wavelet Transform: A New High-Resolution Time-Frequency Representation. IEEE Trans. Signal Process. 2023, 71, 264–278. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, G. Synchrosqueezing-Based Short-Time Fractional Fourier Transform. IEEE Trans. Signal Process. 2023, 71, 279–294. [Google Scholar] [CrossRef]
- Shi, J.; Zheng, J.; Liu, X.; Xiang, W.; Zhang, Q. Novel Short-Time Fractional Fourier Transform: Theory, Implementation, and Applications. IEEE Trans. Signal Process. 2020, 68, 3280–3295. [Google Scholar] [CrossRef]
- Zhang, F.; Bi, G.; Chen, Y.Q. Chip signal analysis by using adaptive short-time fractional Fourier transform. In Proceedings of the 10th European Signal Processing Conference, Tampere, Finland, 4–8 September 2000; pp. 1–4. [Google Scholar]
- Stankovi’c, L.; Alieva, T.; Bastiaans, M.J. Time-frequency signal analysis based on the windowed fractional Fourier transform. Signal Process. 2003, 83, 2459–2468. [Google Scholar] [CrossRef]
- Tao, R.; Lei, Y.; Wang, Y. Short-time fractional Fourier transform and its applications. IEEE Trans. Signal Process. 2010, 58, 2568–2580. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Gao, Z.; Chen, L.; Gao, J.; Xu, Z. The Synchrosqueezed Method and Its Theory-Analysis-Based Novel Short-Time Fractional Fourier Transform for Chirp Signals. Remote Sens. 2024, 16, 1173. https://doi.org/10.3390/rs16071173
Li Z, Gao Z, Chen L, Gao J, Xu Z. The Synchrosqueezed Method and Its Theory-Analysis-Based Novel Short-Time Fractional Fourier Transform for Chirp Signals. Remote Sensing. 2024; 16(7):1173. https://doi.org/10.3390/rs16071173
Chicago/Turabian StyleLi, Zhen, Zhaoqi Gao, Liang Chen, Jinghuai Gao, and Zongben Xu. 2024. "The Synchrosqueezed Method and Its Theory-Analysis-Based Novel Short-Time Fractional Fourier Transform for Chirp Signals" Remote Sensing 16, no. 7: 1173. https://doi.org/10.3390/rs16071173
APA StyleLi, Z., Gao, Z., Chen, L., Gao, J., & Xu, Z. (2024). The Synchrosqueezed Method and Its Theory-Analysis-Based Novel Short-Time Fractional Fourier Transform for Chirp Signals. Remote Sensing, 16(7), 1173. https://doi.org/10.3390/rs16071173