Construction of Aerosol Model and Atmospheric Correction in the Coastal Area of Shandong Peninsula

Abstract

Applying standard aerosol models for atmospheric correction in nearshore coastal waters introduces significant uncertainties due to their inability to accurately represent aerosol characteristics in these regions. To improve the accuracy of remote sensing reflectance ($R_{rs}$) products in the nearshore waters of the Shandong Peninsula, this study develops an aerosol model based on aerosol data collected from the Mu Ping site in the coastal area of the Shandong Peninsula, enabling tailored atmospheric correction for this specific region. Given the pronounced seasonal variations in aerosol optical properties, monthly aerosol models were developed. The monthly aerosol model is derived using the average values of aerosol microphysical properties. Compared to the standard aerosol model, this model is more effective in characterizing the absorption and scattering characteristics of aerosols in the study area. Corresponding lookup tables for the aerosol model were created and integrated into the NIR-SWIR atmospheric correction algorithm. According to the accuracy evaluation indexes of RMSD, MAE, and UPD, it can be found that the atmospheric correction results of the aerosol model established in this paper are better than those of the standard aerosol model, especially in the 547 nm band. It demonstrates that the new aerosol model outperforms the standard model in atmospheric correction performance. With the increasing availability of aerosol observational data, the aerosol model is expected to become more accurate and applicable to other satellite missions.

1. Introduction

Ocean color remote sensing provides abundant observational data for studying water color constituents, including chlorophyll-a concentration, suspended sediment concentration, and water transparency [1,2]. These water color constituents can be inferred using inversion algorithms constructed with remote sensing reflectance ($R_{rs}$) at different spectral bands as variables. Remote sensing reflectance is typically defined as the ratio of radiance leaving the water ($L_w$) to the downwelling irradiance just above the water surface ($E_d$). The signal outside the water constitutes only a small fraction of the signal received by the satellite, with the majority originating from interactions with aerosols and Rayleigh molecules. This atmospheric signal contributes approximately 80% to 90% of the satellite signal in the visible light spectrum over the ocean [3,4]. Additionally, it is subject to subtle influences such as glint and whitecaps. Therefore, obtaining accurate water-leaving signals requires the crucial step of mitigating the impact of aerosols and Rayleigh molecules. Due to the relatively stable composition of molecules in the atmosphere, the portion of Rayleigh molecular scattering can be accurately assessed by considering the influences of polarization, surface pressure, and roughness [5,6]. It is evident from this that mitigating the impact of aerosol components is particularly crucial for obtaining accurate water-leaving signals. As is well known, atmospheric aerosol properties exhibit significant variability across both temporal and spatial scales. Differences in geographical location and time can lead to pronounced disparities in aerosol optical and microphysical characteristics [7]. Consequently, developing an appropriate aerosol model for the relevant satellite images is crucial for eliminating aerosol signals and achieving effective atmospheric correction [8].

The microphysical and optical properties of aerosols, such as particle size distribution and complex refractive index, effectively characterize the features of regional aerosols. They contribute to the successful elimination of aerosol signals during atmospheric correction processes, thus obtaining accurate $R_{rs}$ products [9]. However, characterizing these aerosol properties proves challenging due to their significant temporal and spatial variability [10]. To improve this situation, many studies began analyzing various aerosol observational data to characterize aerosol properties. By constructing different aerosol models, they aim to characterize the absorption and scattering characteristics of aerosols under different temporal and spatial conditions [11,12,13].

Aerosol particle size distribution is an important indicator for studying the origin and distribution of aerosols, and it is commonly incorporated as one of the aerosol model parameters [14,15]. The aerosol size distribution is commonly characterized using the classical log-normal distribution theory, which assigns specific parameters to each component, including modal radius and standard deviation [16]. Several other studies utilize power functions, gamma functions, and analytical functions to depict aerosol particle sizes and their distribution [17,18,19,20]. Based on size distribution, aerosols are classified into five categories (rural, urban, maritime, tropospheric, and fog) by Shettle and Fenn, commonly known as SF79 [12]. In establishing relevant aerosol models, they further consider the impact of relative humidity on each group of aerosol particles. Gordon and Wang [21] were the first to apply three SF79 aerosol models (maritime, coastal, and tropospheric) in atmospheric correction for ocean color remote sensing satellite imagery. Chomko and Gordon introduced maritime, coastal, tropospheric, and urban aerosol models [17].

Ahmad et al. [22] categorized aerosol types into 10 categories and combined them with eight relative humidity levels to form 80 aerosol models (referred to as AF10). They constructed corresponding lookup tables for each model. Among these, the fine-mode particle component of the 10 aerosol types is comprised of 99.5% dust particles and 0.5% soot particles, showing excellent consistency with the average results of aerosol optical properties measured by AERONET. These 10 aerosol models have varying proportions of coarse and fine modal particles but share the same effective radius and mean radius [5,22]. These aerosols can be used to eliminate aerosol signals during the atmospheric correction process. However, due to the limitations of the models themselves, they cannot effectively account for the presence of strongly absorbing aerosols. These aerosols often occur in coastal waters where aerosols from land are transported to the sea due to wind advection effects, even extending into the open ocean. To effectively characterize the characteristics of strongly absorbing aerosols, many researchers focused their studies on this aspect [10]. However, during the atmospheric correction process, there is no reliable method to detect the presence of absorbing aerosols in the Near-Infrared (NIR) band. As a consequence, all pixels are processed using non-absorbing or weakly absorbing aerosol algorithms [5].

Current atmospheric correction algorithms often overestimate aerosol radiance in coastal marine areas, leading to the underestimation of water-leaving signals, particularly near the blue spectral bands, and even negative remote sensing reflectance values may occur [6]. This situation may arise because AERONET sites are primarily located on land, with fewer stations situated in marine areas, and their global distribution is not uniform. As a result, the observed data from AERONET sites used for constructing aerosol models are limited, with a mere 11 sites situated in open oceans and adjacent coastal waters. In coastal waters, influenced by both land and sea, aerosol sources are more complex. Merely relying on observed marine data to characterize aerosol conditions with complex sources in coastal areas poses challenges [1]. Given this limitation, other studies started to collect more aerosol observational data and integrate it into aerosol models [22,23]. Some researchers utilize continuously updated AERONET datasets to build new aerosol models for studying specific regions [24]. One study divided 27 aerosol models based on global AERONET aerosol observational data to improve the inadequacy of AF10 in effectively characterizing strongly absorbing aerosols [25]. In this research, we attempt to utilize aerosol observation data from the Yellow Sea Offshore Verification Platform established by the National Satellite Ocean Application Center. We aim to construct aerosol models and Look-Up Tables (LUTs) specifically for the nearshore region of the Shandong Peninsula in China. This endeavor is undertaken to achieve more accurate remote sensing reflectance (Rrs) inversion products for the coastal waters of China.

2. Materials and Methods

2.1. Materials

2.1.1. Sun/Sky Photometer Data

The Mu Ping site (37.681N, 121.700E) is located in the coastal area approximately 20 km north of the coastline in the Mu Ping district of Yantai City, Shandong Province, as shown in Figure 1. Situated near the junction of the Bohai Sea and Yellow Sea, this site experiences a dual influence from both the ocean and the mainland due to its proximity to the coastline. The station employs the CE318 Sun Photometer, a water color version manufactured by the French company CIMEL Electronics. It comprises 11 observation channels at wavelengths of 400 nm, 412 nm, 442 nm, 490 nm, 510 nm, 560 nm, 620 nm, 665 nm, 779 nm, 865 nm, and 1020 nm. In atmospheric aerosol research, the wavelengths of 442 nm, 665 nm, 865 nm, and 1020 nm are commonly used [26]. The instrument primarily measures solar radiance, allowing for the estimation of atmospheric aerosol characteristics and other components.

The CE318 multi-band sun photometer, using the PhotoGetData (v2.18.5) software, can transmit the measured data through the RS232 serial port to a computer and save it, generating binary storage files (K8 files). Each K8 file, after conversion into ASCII format, typically includes multiple file types with different suffixes. Among them, the NSU file represents data for direct solar radiation measurements, primarily used for calculating aerosol optical thickness and other parameters. The ALL and ALR files, respectively, denote data for zenith angle scans in the sky and left–right scans along the azimuth circle, mainly used for inverting sky radiance parameters. The sun photometer data at this site are sourced from the National Satellite Ocean Application Center.

2.1.2. Remote Sensing Images

MODIS is equipped with 36 spectral bands, among which 16 are primarily suitable for water color research, including 10 visible bands, 3 Near-Infrared bands, and 3 Short-Wave Infrared bands. The high temporal resolution of MODIS sensor provides significant advantages for studying rapidly changing water color in time dynamics, making it one of the widely used image data globally. For turbid coastal waters, MODIS’s Short-Wave Infrared bands can effectively serve atmospheric correction work. MODIS sensor provides various level data products, including L0, L1A, L1B, L2, and L3. L0 data are the raw data received by the sensor without processing, which is only used in a few specific applications. L1A data are reconstructed from L0 data and supplemented with auxiliary information (including radiometric and geometric calibration coefficients, as well as geolocation parameters). L1B data are radiometrically calibrated L1A data. L2 data are the geophysical products developed by combining L1B data with auxiliary data through processes such as atmospheric correction and parameter inversion. L3 data are raster data obtained by uniform mosaicking and projecting L2 products over a certain geographic grid within a certain time period. In this article, MODIS Aqua L1A data are used as the source of remote sensing image data to validate the atmospheric correction results obtained from aerosol models. The data were downloaded from NASA (https://oceancolor.gsfc.nasa.gov/, accessed on 1 October 2023).

2.1.3. R_rs Validation Data

This study utilizes on-site measurements of $R_{rs}$ spectra from the Mu Ping station, established by the National Satellite Ocean Application Center on the northern coast of the Shandong Peninsula. The dataset includes measurements collected from the year 2020 to the present. When conducting measurements, the method used was that recommended by NASA for obtaining above-water remote sensing reflectance ($R_{rs}$) data [27], which were estimated as

$$R_{rs}=\frac{{\rho }_p\left(L_u-{\rho }_f\times L_{sky}\right)}{\pi L_{pla}}$$

(1)

where $L_u$ is the upward radiance, $L_{sky}$ denotes skylight radiance,${ L}_{pla}$ represents the radiance emitted from a standard reference plaque, all of which were directly measured using a spectrometer. ${\rho }_p$ represents the reflectance (approximately 10%) of a standard reference plaque provided by the producer, and ${\rho }_f$ signifies the Fresnel reflection off the water surface, assumed to be 0.022 for a flat water surface.

2.2. Methods

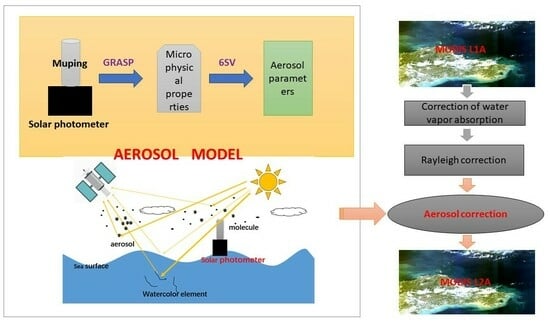
2.2.1. Construction of Aerosol Models

The raw data used for the inversion of aerosol microphysical properties comes from the Mu Ping station’s CE318 Water Color Sun/Sky Photometer. The microphysical characteristics of aerosols, including particle size distribution and complex refractive index, can be inferred from spectral sky radiance measurements conducted at 442, 665, 865, and 1020 nm, obtained at the almucantar plane, along with solar direct irradiance measurements at corresponding wavelengths [26]. The selected four bands exhibit no significant gas absorption and demonstrate high sensitivity to the typical sizes of major aerosols [28]. Before the inversion of microphysical properties, it is necessary to select data that meet certain criteria. First, the observed sky radiance data from both left and right azimuth scans (clockwise and counterclockwise) should differ by no more than 20%. The average of the left and right azimuth scan data is then taken as the sky radiance data for that specific time point. Second, under the condition of symmetric azimuth angles for left and right sky scattering radiance, the scattering radiance data used for inversion should have a symmetrical azimuthal angle count greater than 21, within the range of 3.5° to 160° [29]. Third, the selected data should have a solar zenith angle greater than 50°. The data generated under this criterion is similar to the AERONET website’s version 2.0 data [29,30]. The sky radiance data were convolved using a square filter with a width of 10 nm centered at the effective wavelengths of the photometer. The standard extraterrestrial spectrum irradiance (https://oceancolor.gsfc.nasa.gov/docs/rsr/f0.txt, accessed on 1 October 2023) was used to normalize the resulting spectra [31].

The Generalized Retrieval of Aerosol and Surface Properties (GRASP) code, developed by Dubovik et al., is an open-source algorithm designed for retrieving properties of aerosols [30,32,33]. GRASP comprises two main modules: numerical inversion and forward modeling. The numerical inversion module employs statistical optimization techniques to fit observational data, while the forward model accurately simulates various atmospheric remote sensing observations [34]. Therefore, this versatility allows GRASP to be applied across passive and active satellites, as well as ground-based atmospheric observations, and it is particularly suited for synergistic retrievals when inverting different observations simultaneously [35]. The algorithm accepts diverse input data, such as satellite images, polar nephelometer measurements, sun/sky photometer data, sky camera images, and lidar data. The precise inversion of various combinations of these input data is accomplished through the use of a multi-term least squares method (LSM) [36]. This fitting algorithm can undergo statistical optimization, allowing for flexible inversions based on different observations [37]. In this study, ground-based observations from a single sun photometer were utilized for the inversion of aerosol properties. The retrieved column-integrated aerosol volume size distributions (VSDs) are adjusted using 22 logarithmically equidistant triangle bins ranging from 0.05 to 15 µm in radius [38]. While some studies suggest approximating VSDs with bimodal log-normal distributions to reduce the information required by the binned VSDs, a problem arises when the retrieved VSDs deviate from perfect log-normality, leading to asymmetrical or trimodal shapes. In such cases, the strategy based on simplified bimodal VSDs may not yield accurate retrievals, hence the preference for the former approach despite its more complex calculations. To further validate the algorithm’s reliability and ensure the accuracy of the results, we selected raw data from the AERONET Beijing_PKU and Socheongcho sites as input for the GRASP algorithm [39]. We inverted the aerosol particle size distribution for the respective regions of these two sites. The Beijing_PKU site is located on land, and the data selected are from 1 January 2019, at 01:21:13 UTC. The Socheongcho site is situated in the ocean, and the data retrieved are from 3 January 2020, at 03:48:35 UTC. These two sites represent different underlying surface types. The obtained results are shown in Figure 2.

For the Beijing_PKU site, it can be observed that the trend of aerosol size distribution obtained by the GRASP algorithm is generally consistent with the AERONET results. However, a notable difference is that the AERONET results exhibit higher peaks at the coarse and fine modal particles compared to the GRASP results. For the Socheongcho site, the consistency between GRASP and AERONET results is nearly perfect, with only minor differences observed at the peak of coarse-mode particles. This suggests that the GRASP algorithm is capable of accurately retrieving aerosol characteristics in the respective regions.

In open ocean regions, the distribution of aerosol particles in the air above the sea surface is relatively stable, with less influence from external factors, and the composition and concentration of aerosols change minimally with the seasons [22]. However, in coastal areas, due to proximity to land, the composition of aerosols in the atmosphere above undergoes rapid changes in both time and space, influenced significantly by human activities and natural factors on land, and is subject to larger variations due to terrestrial influences [40].

The AF10 model, currently adopted as the globally standardized aerosol model by NASA, incorporates relative humidity as a key parameter to adapt various regional aerosol models. However, aerosol particles originating from terrestrial sources, including continental, biomass burning, and dust sources, demonstrated limited sensitivity to variations in relative humidity, particularly under conditions where the relative humidity is below 70% [41,42]. Kinne’s study of aerosol characteristics on the monthly average time scale found that large monthly differences were rare [43]. Sang Woo studied the optical properties of columnar aerosols in East Asia and found that their changes had seasonal and monthly characteristics [44]. Through studying the global aerosol particle size distribution and complex refractive index parameters, Zhao Dan found that these parameters changed slightly in the same month in different years and were relatively stable [1]. Therefore, for more accurate construction of regional aerosol models, this study builds aerosol models for the region based on monthly aerosol data. Selecting the sun photometer data from the Mu Ping station between 2020 and 2022, which underwent quality control, the GRASP algorithm is employed to invert aerosol microphysical and optical properties. Results with inversion fitting errors of less than 5% are considered valid. Valid results are then statistically analyzed, and monthly averages are calculated to construct monthly aerosol models. The microphysical properties of aerosols, including particle size distribution and complex refractive index, along with optical properties such as extinction coefficient, Ångström exponent (α), single scattering albedo (SSA), and aerosol phase function, can be simulated using a radiative transfer model predicated on these pivotal microphysical attributes [45].

The aerosol size distribution function describes how particles of different diameters are distributed within a given volume. Typically, this function is modeled as the combination of two log-normal distributions: one for fine particles and the other for coarse particles. This combined distribution is commonly known as a bimodal log-normal distribution. Mathematically, it can be represented as follows:

$$\frac{dV\left(r\right)}{dlnr}=\frac{V_f}{\sqrt{2\pi }{\sigma }_f}\exp \left[-{\left(\frac{lnr-ln{r}_f}{\sqrt{2}{\sigma }_f}\right)}^2\right]+\frac{V_c}{\sqrt{2\pi }{\sigma }_c}\exp \left[-{\left(\frac{lnr-ln{r}_c}{\sqrt{2}{\sigma }_c}\right)}^2\right]$$

(2)

where V denotes the volume concentration of the particles, r represents the mean volume radius of the particles, $f$ and $c$ represent coarse mode particles and fine mode particles, respectively. $r_f$ and $r_c$ represent the mean volume radius of the fine and coarse mode particles, respectively. ${\sigma }_f$ and ${\sigma }_c$ signify the standard deviation of the fine mode and coarse mode particle size within a model. Figure 3 shows the monthly average particle size distribution at the Mu Ping station for months 1 to 12 [43]. The complex refractive index comprises the real part ($n_r$) and the imaginary part ($n_i$), which vary depending on the chemical composition of the aerosol; $n_r$ and $n_i$ govern the scattering and absorption of aerosols by incident light, respectively [46,47]. Figure 4 illustrates the distribution of the real and imaginary components of the complex refractive index at 442 nm across months 1 to 12. In July, there is only one valid data point, and thus, it lacks monthly representativeness. By inputting the aforementioned particle size distribution and complex refractive index into the 6S radiative transfer model, the optical properties of aerosols can be simulated [48].

2.2.2. Construction of the Lookup Table for the New Aerosol Model

These tables contain parameters identical to those used in the AF10 model. Additionally, two sets of coefficients were computed. The first set represents the correlation between single-scattering albedo and multiple-scattering albedo. The second set of coefficients relates to the relationship between diffuse transmittance from the sun to Earth’s surface, diffuse transmittance from the surface to the satellite, and aerosol optical thickness.

In the case where geometric conditions and aerosol optical thickness (AOD) are known, the relationship between aerosol single-scattering reflectance (${\rho }_{as}$) and aerosol multiple-scattering reflectance (${\rho }_a$) can be expressed as

$$ln\left[{\rho }_a\left(\lambda \right)\right]=a\left(\lambda \right)+b\left(\lambda \right)ln\left[{\rho }_{as}\left(\lambda \right)\right]+c\left(\lambda \right){ln}^2\left[{\rho }_{as}\left(\lambda \right)\right]$$

(3)

$${\rho }_{as}\left(\lambda \right)={\omega }_a\left(\lambda \right){\tau }_a\left(\lambda \right)p_a({\theta }_s,{\theta }_v,\varphi ,\lambda )/4cos{\theta }_{v}cos{\theta }_s$$

(4)

$$p_a\left({\theta }_s,{\theta }_v,\varphi ,\lambda \right)=P_a\left({\theta }_{-},\lambda \right)+(r\left({\theta }_s\right)+r\left({\theta }_v\right))P_a({\theta }_{+},\lambda )$$

(5)

$$cos{\theta }_{\pm }=\pm cos{\theta }_{s}cos{\theta }_v-sin{\theta }_{s}sin{\theta }_v\mathrm{c}\mathrm{o}\mathrm{s}\varphi$$

(6)

where ${\omega }_a$ is aerosol single scattering albedo, ${\tau }_a$ is aerosol optical depth, ${\theta }_s$ and ${\theta }_v$ are solar zenith angle and view zenith angle, respectively, $\varphi$ is relative azimuth angle, $P_a\left({\theta }_{\pm },\lambda \right)$ is the aerosol scattering phase function for a scattering angle, ${\theta }_{\pm }$, $r\left(\theta \right)$ is the Fresnel reflectance of the interface for an incident angle $\theta$.

Whereas the multiple-scattering reflectance is obtained through simulations using the 6S radiative transfer model [48], the single-scattering reflectance is calculated using Equations (4) and (5) [49].

By employing the method of least squares fitting regression to solve for the coefficients a, b, and c, the relationship between $ln{\rho }_a$ and $ln{\rho }_{as}$ under specific geometric conditions (${\theta }_s=36$°, ${\theta }_v=66$°, $\varphi =70$°) for the aerosol model at the Mu Ping station in June is depicted in Figure 5. The regression coefficients in the regression equation correspond to the a, b, and c in Equation (3).

The relationship between diffuse transmittance t ($t_s$ or $t_v$) and aerosol optical depth (${\tau }_a$) can be expressed as

$$t=Aexp(-B{\tau }_a)$$

(7)

Whereas the diffuse transmittance t is obtained through simulations using the 6S radiative transfer model under specific geometric parameters and AOD conditions, the coefficients (A and B) can be obtained through the least squares fitting method. Figure 6 depicts the relationship between diffuse transmittance and aerosol optical depth when the solar zenith angle is 36 degrees, and the coefficients of the fitting equation correspond to the A and B in Equation (7).

For each lookup table (LUT) associated with the aerosol model for each month, we integrated diverse combinations of aerosol multiple-scattering and diffuse transmittance coefficients correlated with aerosol optical depth (AOD) values and satellite/solar geometric parameters. In particular, the AOD varied from 0 to 3 (with an increment of 0.1), while the solar/sensor zenith angles (${\theta }_s$ and ${\theta }_v$) ranged from 0 to 78 degrees (with an increment of 6 degrees), and their relative azimuthal angles ($\varphi$) ranged from 0 to 180 degrees (with an increment of 10 degrees). Conversely, NASA’s LUT employed only 8 AOD values within a significantly narrower range [4]. The format and content of the aerosol lookup table are shown in

Table 1. Aerosol lookup table LUTs parameter list.

Parameter	Description	Dimension
wave	wavelength	1
scatt	scattering angle	1
albedo	single scattering albedo	1
extc	extinction coefficient	1
angstrom	Ångström index	1
phase	Scattering Phase Function	2
solz	Solar zenith angle	1
senz	View zenith angle	1
phi	Relative azimuth	1
accost bcost ccost	Aerosol single-multiple scattering coefficient	4
dtran_wave	Diffuse transmission wavelength	1
dtran_theta	Diffuse transmission zenith angle	1
$\text{dtran\_a} (a_0$$) \text{dtran\_b} (b_0$)	Diffuse transmittance coefficient	2

.

2.2.3. Atmospheric Correction

The radiative signals observed by satellite sensors include signals from both water bodies and the atmosphere [21,50]. To achieve more accurate retrieval of water color elements, it is essential to separate the water color signal from the atmospheric signal [51,52,53]. The process of removing the atmospheric signal is known as atmospheric correction [54,55].

The goal of atmospheric correction is to establish specific models that remove atmospheric path and surface influences from the Top of Atmosphere (TOA) signals. The primary difficulty involves accurately assessing the impact of aerosols, a major source of uncertainty in atmospheric correction, on atmospheric path radiance. This contribution varies considerably and must be estimated based on observations [56]. Water exhibits strong absorption in the Near-Infrared to Short-Wave Infrared (NIR-SWIR) range, providing a basis for separating atmospheric and ocean signals [57,58]. Initially, for open ocean regions, SeaWiFS and MODIS atmospheric correction was conducted using two Near-Infrared (NIR) bands under the assumption that the marine influence in these NIR bands could be considered negligible [50]. However, coastal regions, influenced by factors such as land–sea dynamics, often have turbid waters. In these areas, the radiance observed in the Near-Infrared (NIR) bands can be significant. This can pose challenges for iterative methods that rely solely on NIR, leading to underestimation or even negative values for water-leaving radiance. To tackle this issue, Wang et al. [59] proposed an atmospheric correction algorithm for MODIS that incorporates both Near-Infrared and Short-Wave Infrared bands. The key aspect of this algorithm involves introducing a turbidity index based on MODIS measurements in the Near-Infrared (748 nm) and Short-Wave Infrared bands (1240 nm, 2130 nm), as described in Equation (7). When the turbidity index meets certain conditions $T_{ind}\left(748, 1240\right)<1.3$, the iterative method using Near-Infrared bands (748 nm, 869 nm) is applied; otherwise, the iterative method using Short-Wave Infrared bands (1240 nm, 2130 nm) is utilized [59,60].

$$T_{ind}\left(748, 1240\right)=\frac{\mathsf{\Delta }{\rho }^{\left(RC\right)}\left(748\right)}{\mathsf{\Delta }{\rho }^{\left(RC\right)}\left(1240\right)}exp\left\{-\frac{492}{890}ln\left(\frac{\mathsf{\Delta }{\rho }^{\left(RC\right)}\left(1240\right)}{\mathsf{\Delta }{\rho }^{\left(RC\right)}\left(2130\right)}\right)\right\}$$

(8)

$$\mathsf{\Delta }{\rho }^{\left(RC\right)}\left({\lambda }_l\right)={\rho }_t\left({\lambda }_l\right)-{\rho }_r\left({\lambda }_l\right)$$

(9)

where ${\rho }_t\left({\lambda }_l\right)$ represents the reflectance of the top atmosphere observed by satellites after gas absorption correction, and ${\rho }_r\left({\lambda }_l\right)$ denotes the reflectance contributed by the molecules, also known as Rayleigh scattering.

3. Results

To further validate the efficacy of our new aerosol model in improving atmospheric correction, we applied the previously described NIR-SWIR atmospheric correction algorithm. This algorithm, recommended jointly by NASA for turbid water bodies, was validated utilizing datasets on a global and regional scale. The monthly Look-Up Tables (LUTs) developed for the study sites in this research were substituted for the standard LUTs in the SeaDAS (v8.3) software. During the atmospheric correction process for a specific pixel, the aerosol LUT is selected based on the location of the target pixel and the month of data collection. Subsequently, this LUT is utilized to estimate the aerosol scattering component of the signal [1].

This research utilized the same version of SeaDAS (v8.3) for the removal of gas absorption and Rayleigh scattering to assess the improvements of the new aerosol model on remote sensing reflectance ($R_{rs}$) products. We established specific criteria for selecting corresponding satellite and in situ observational data. Initially, the time interval between satellite observations and ground-based measurements was limited to 30 min. While NASA’s standard allows a 3 h time difference in open ocean regions, our stricter criterion was necessary due to the higher variability and influence of continental factors in coastal areas. Pixels identified as being affected by cloud or ice contamination, having high sensor view zenith, high solar zenith, and stray light contamination were deemed invalid. Instead of using NASA’s default Rayleigh-corrected reflectance for cloud-masked reflectance, we opted for an alternative approach [1]. This decision was made due to concerns that NASA’s default threshold might incorrectly identify turbid water or thick aerosols, which are common in coastal waters. Similar methodologies were adopted in previous research studies [61,62].

Figure 7 shows the remote sensing reflectance ($R_{rs}$) obtained from the aerosol model developed in this study and the AF10 aerosol model processed through the NIR-SWIR algorithm. It can be observed that the $R_{rs}$ distribution from the two models is generally consistent, with subtle differences in specific values. In certain regions, the aerosol model established in this article yields slightly higher $R_{rs}$ than the NASA standard model. This means that the aerosol signals assessed by standard aerosol models in these regions may be higher than those in the aerosol models presented in this paper. This is due to the fact that standard aerosol models are constructed using only a small number of observations from ocean sites, especially in coastal areas. This results in the overestimation of aerosol signals in turbid water, while the measured aerosol data in this paper can better characterize the aerosol characteristics of the study area, and the aerosol signals obtained are more accurate. Figure 8 presents a further comparison between satellite-retrieved $R_{rs}$ and ground-based measured $R_{rs}$ spectra. For this collection of spectra, in strict adherence to the previously defined criteria, the time gap between satellite imagery and ground measurements does not exceed 30 min. It can be seen that when we use the new aerosol model, the results calculated by the NIR-SWIR algorithm are closer to the measured values.

4. Discussion

We use several accuracy assessment metrics to evaluate the results of the aerosol model, encompassing the regression slope, coefficient of determination ($R^2$), root mean squared difference (RMSD), unbiased percentage difference (UPD), and mean absolute error (MAE).

$$RMSD=\sqrt{\frac{1}{N}\sum _{i=1}^N{(Y_i-X_i)}^2}$$

(10)

$$MAE=\frac{1}{N}\sum _{i=1}^N\left|Y_i-X_i\right|$$

(11)

$$UPD=\sum _{i=1}^N\frac{\left|Y_i-X_i\right|}{0.5\times \left|Y_i+X_i\right|}$$

(12)

Figure 9 displays the satellite data alongside corresponding measurements for three visible bands (i.e., 443, 547, and 645 nm), and the satellite $R_{rs}$ product is also calculated using the NIR-SWIR algorithm. The red points represent the results of NASA’s standard aerosol model, while the blue points represent the results of the new aerosol model proposed in this study.

From the results, it is clear that for the RMSD, MAE, and UPD accuracy evaluation indicators, the results of the new model are significantly better than NASA’s standard model. For $R^2$ and slope, except for slightly lower values at 645 nm, the new model’s results at 443 nm and 547 nm are also better than the standard model.

Table 2. The evaluation metrics for the atmospheric correction results of the nine MODIS bands, evaluated using in situ $R_{rs}$ dataset from the Mu Ping site.

	Band	${\mathit{R}}^2$	Slope	RMSD	MAE	UPD (%)
Our/NASA model	412	0.56/0.53	0.71/0.6	0.003/0.0037	0.0022/0.0029	41.68/49.13
	443	0.61/0.6	0.78/0.77	0.0029/0.0036	0.0023/0.0028	32.12/40.29
	469	0.65/0.64	0.76/0.77	0.0032/0.0039	0.0026/0.0031	28.48/38.04
	488	0.57/0.66	0.6/0.77	0.0038/0.0039	0.0031/0.0031	27.01/32.86
	531	0.76/0.69	0.84/0.79	0.0033/0.0042	0.0025/0.0033	21.93/28.69
	547	0.82/0.68	0.86/0.76	0.0029/0.0044	0.0023/0.0034	19.46/27.69
	555	0.62/0.65	0.7/0.72	0.0045/0.0048	0.0037/0.0037	49.41/31.14
	645	0.64/0.73	0.81/0.83	0.0018/0.0023	0.0014/0.0018	42.00/46.28
	678	0.62/0.72	0.74/0.82	0.0014/0.0019	0.0012/0.0015	40.49/43.32

lists the accuracy assessment statistics for MODIS’s nine bands. Overall, the performance of the new aerosol model is better than the standard aerosol model, especially at 547 nm. It is important to highlight that the underestimation observed in the blue light band with the new model, relative to the standard model, was mitigated, which is likely attributed to a more accurate representation of absorbing aerosols [1]. It is notable that the slopes observed in these bands are all less than 1, possibly indicating the overcorrection of remote sensing reflectance ($R_{rs}$) in turbid water. Please note that the study initially matched 24 satellite situ points. However, minor discrepancies in the number of data points across different models or bands may arise from saturation or negative $R_{rs}$ values in MODIS bands or from the atmospheric correction process.

5. Conclusions

Coastal regions, characterized by complex water compositions, introduce significant uncertainties in remote sensing reflectance ($R_{rs}$) obtained through atmospheric correction. NASA’s aerosol models are primarily developed for open ocean conditions, leading to substantial variability in coastal areas, mainly due to the inaccurate characterization of absorbing aerosols in the aerosol correction process. In this study, aerosol observation data from the Mu Ping station in the Yellow and Bohai Seas were utilized to characterize aerosol properties in the region. Aerosol properties, such as single scattering albedo (SSA) and Ångström exponent, exhibited noticeable spatial gradients and seasonal dynamics. The monthly aerosol model, based on these aerosol characteristics by taking their monthly averages, can more effectively characterize the scattering and absorption properties of aerosols in the region, facilitating the precise removal of aerosol signals from the sensor-received signals. By incorporating this aerosol model and the standard aerosol model into the NIR-SWIR algorithm for atmospheric correction, the atmospheric correction results for both models in the region are obtained. These results are then matched and validated against measured data. From the precision evaluation metrics, including RMSD, MAE, and UPD, it can be observed that the new aerosol model outperforms the standard aerosol model across the nine visible light bands of MODIS, leading to an improvement in the accuracy of atmospheric correction.

While we only applied this aerosol model to MODIS satellite imagery in this study, it can seamlessly be adapted for use with other satellite imagery. This adaptation requires constructing aerosol model lookup tables that align with the specific wavelength bands of the other satellites. This opens up the possibility of generating additional remote sensing reflectance ($R_{rs}$) products for coastal regions, facilitating the improved retrieval of water color-related parameters.

Certainly, there is substantial room for improvement in the current aerosol model. The model’s construction was based on observational data from the Mu Ping station spanning 2020 to 2022, which is relatively limited. As time progresses, the Mu Ping station will provide more observational data, enabling the aerosol model to better capture the seasonal dynamic changes in aerosol characteristics. This will facilitate more effective atmospheric correction efforts. Depending on requirements, aerosol models can be constructed with smaller time intervals. Presently, the Huangdonghai offshore observation platform has deployed two observation stations, Mu Ping and Dongtou. In the future, more aerosol observation stations will be established in China’s offshore areas, achieving comprehensive coverage of aerosol characteristic observations in the Chinese near seas. This holds extraordinary significance for obtaining precise $R_{rs}$ products in China’s nearshore regions.