Estimation and Validation of Land Surface Temperatures from Chinese Second-Generation Polar-Orbit FY-3A VIRR Data
Abstract
:1. Introduction
2. Data
2.1. FY-3A Satellite Data
| Channel No. | Spectral Range (µm) | IFOV (km) | NE Δρ (%) NE ΔT (300 K) | Dynamic Range (ρ or T) |
|---|---|---|---|---|
| 1 | 0.58–0.68 | 1.1 | 0.1% | 0%–100% |
| 2 | 0.84–0.89 | 1.1 | 0.1% | 0%–100% |
| 3 | 3.55–3.93 | 1.1 | 0.3 K | 180–350 K |
| 4 | 10.3–11.3 | 1.1 | 0.2 K | 180–330 K |
| 5 | 11.5–12.5 | 1.1 | 0.2 K | 180–330 K |
| 6 | 1.55–1.64 | 1.1 | 0.15% | 0%–90% |
| 7 | 0.43–0.48 | 1.1 | 0.05% | 0%–50% |
| 8 | 0.48–0.53 | 1.1 | 0.05% | 0%–50% |
| 9 | 0.53–0.58 | 1.1 | 0.05% | 0%–50% |
| 10 | 1.325–1.395 | 1.1 | 0.19% | 0%–90% |
2.2. MODIS Satellite Data
2.3. In Situ Measurements

3. Methodology
3.1. Radiative Transfer for the Split-Window Algorithm
3.2. Algorithm Development for FY-3A VIRR Data




| Variable | Tractable Sub-Range | Overlap |
|---|---|---|
| Water vapor content (WVC) (g/cm2) | [0, 1.5], [1.0, 2.5], [2.0, 3.5], [3.0,4.5], [4.0, 5.5], [5.0, 6.5] | 0.5 |
| Land surface temperature (LST) (K) | ≤280, [275, 295], [290, 310], [305, 325], ≥320 | 5.0 |
| Conditions | WVC [1.0, 2.5] Ts [275 K, 295 K] | ||||||
|---|---|---|---|---|---|---|---|
| Emissivity | 1/cos(VZA) | b0 | b1 | b2 | b3 | b4 | b5 |
| 1.0 | 6.1589 | 0.9799 | 2.1183 | −0.0819 | 50.4947 | −97.6539 | |
| 1.2 | 7.2545 | 0.9764 | 2.2088 | −0.0700 | 49.9067 | −97.4687 | |
| 1.4 | 8.3196 | 0.9730 | 2.2919 | −0.0579 | 49.3379 | −97.0982 | |
| 1.6 | 9.3640 | 0.9696 | 2.3681 | −0.0454 | 48.7807 | −96.5531 | |
| 1.8 | 10.3950 | 0.9662 | 2.4369 | −0.0327 | 48.2272 | −95.8291 | |
| 2.0 | 11.4044 | 0.9629 | 2.4995 | −0.0199 | 47.6776 | −94.9575 | |
| 1.0 | 3.8681 | 0.9889 | 1.8190 | −0.0395 | 47.9444 | −85.0717 | |
| 1.2 | 4.5454 | 0.9869 | 1.9230 | −0.0297 | 47.5162 | −86.0962 | |
| 1.4 | 5.1831 | 0.9850 | 2.0150 | −0.0197 | 47.0893 | −86.6894 | |
| 1.6 | 5.7910 | 0.9831 | 2.0973 | −0.0094 | 46.6635 | −86.9527 | |
| 1.8 | 6.3789 | 0.9814 | 2.1713 | 0.0009 | 46.2359 | −86.9394 | |
| 2.0 | 6.9440 | 0.9797 | 2.2383 | 0.0113 | 45.8088 | −86.7118 | |
3.3. Determination of LSEs
3.3.1. Bare Soil Pixels

3.3.2. Fully Vegetated Pixels
3.3.3. Mixed Pixels
3.4. Determination of Atmospheric WVC
4. Results and Discussion
4.1. Estimation of LST


4.2. Sensitivity Analysis
4.2.1. Instrument Noise (NEΔT)
4.2.2. Land Surface Emissivity
4.2.3. Atmospheric WVC
4.2.4. Total Error
5. Validation
5.1. Validation Using the Simulated Data

5.2. Validation Using the MODIS LST Product MOD11_L2


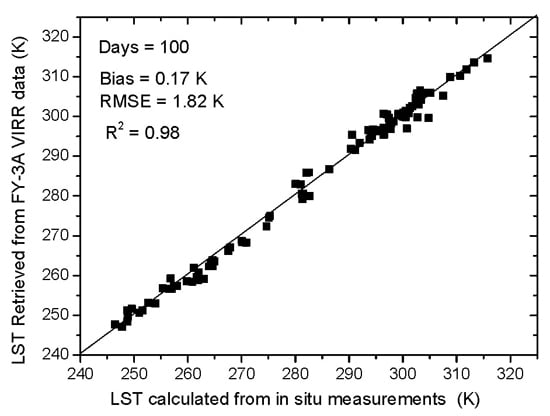
5.3. Validation Using In Situ Measurements


6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.J.; Wan, Z.; Trigo, I.F.; Sobrino, J. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.-H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Tang, B.-H.; Li, Z.-L. Estimation of instantaneous net surface longwave radiation from MODIS cloud-free data. Remote Sens. Environ. 2008, 112, 3482–3492. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.-H.; Yan, G.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global surface temperature change. Rev. Geophys. 2010, 48, RG4004. [Google Scholar]
- Sobrino, J.A.; Raissouni, N.; Li, Z.-L. A comparative study of land surface emissivity retrieval from NOAA data. Remote Sens. Environ. 2001, 75, 256–266. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jimenez-Munoz, J.C.; Verhoef, W. Canopy directional emissivity: Comparison between models. Remote Sens. Environ. 2005, 99, 304–314. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.-L. Temperature-independent spectral Indices in thermal Infrared bands. Remote Sens. Environ. 1990, 32, 17–33. [Google Scholar] [CrossRef]
- Li, Z.-L.; Becker, F. Feasibility of land surface-temperature and emissivity determination from AVHRR data. Remote Sens. Environ. 1993, 43, 67–85. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.-L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.-L. Radiance-based validation of the V5 MODIS land-surface temperature product. Int. J. Remote Sens. 2008, 29, 5373–5395. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Tang, B.-H.; Bi, Y.; Li, Z.-L.; Xia, J. Generalized Split-Window algorithm for estimate of land surface temperature from Chinese geostationary FengYun meteorological satellite (FY-2C) data. Sensors 2008, 8, 933–951. [Google Scholar] [CrossRef]
- Gao, C.; Tang, B.-H.; Wu, H.; Jiang, X.; Li, Z.-L. A generalized split-window algorithm for land surface temperature estimation from MSG-2/SEVIRI data. Int. J. Remote Sens. 2013, 34, 4182–4199. [Google Scholar] [CrossRef]
- Jiang, G.-M.; Liu, R. Retrieval of sea and land surface temperature from SVISSR/FY-2C/D/E measurements. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6132–6140. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.-L. Validation of the land-surface temperature products retrieved from Terra Moderate Resolution Imaging Spectroradiometer data. Remote Sens. Environ. 2002, 83, 163–180. [Google Scholar] [CrossRef]
- Hook, S.J.; Vaughan, R.G.; Tonooka, H.; Schladow, S.G. Absolute radiometric in-flight validation of mid infrared and thermal infrared data from ASTER and MODIS on the Terra spacecraft using the lake tahoe, CA/NV, USA, automated validation site. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1798–1807. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the MODIS land-surface temperature/emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Schneider, P.; Hook, S.J.; Radocinski, R.G.; Corlett, G.K.; Hulley, G.C.; Schladow, S.G.; Steissberg, T.E. Satellite observations indicate rapid warming trend for lakes in California and Nevada. Geophys. Res. Lett. 2009, 36, 1–6. [Google Scholar]
- Coll, C.; Caselles, V.; Galve, J.M.; Valor, E.; Niclòs, R.; Sanchez, J.M.; Rivas, R. Ground measurements for the validation of land surface temperatures derived from AATSR and MODIS data. Remote Sens. Environ. 2005, 97, 288–300. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Sòria, G.; Prata, A.J. Surface temperature retrieval from Along Track Scanning Radiometer 2 data: Algorithms and validation. J. Geophys. Res. 2004, 109, D11101. [Google Scholar] [CrossRef]
- Coll, C.; Valor, E.; Galve, J.M.; Mira, M.; Bisquert, M.; García-Santos, V.; Caselles, E.; Caselles, V. Long-term accuracy assessment of land surface temperatures derived from the Advanced Along-Track Scanning Radiometer. Remote Sens. Environ. 2012, 116, 211–225. [Google Scholar] [CrossRef]
- Trigo, I.F.; Monteiro, I.T.; Olesen, F.; Kabsch, E. An assessment of remotely sensed land surface temperature. J. Geophys. Res. 2008, 113, D17108. [Google Scholar] [CrossRef]
- Qian, Y.G.; Li, Z.-L.; Nerry, F. Evaluation of land surface temperature and emissivities retrieved from MSG-SEVIRI data with MODIS land surface temperature and emissivity products. Int. J. Remote Sens. 2013, 34, 3140–3152. [Google Scholar] [CrossRef]
- Göttsche, F.-M.; Olesen, F.-S.; Bork-Unkelbach, A. Validation of land surface temperature derived from MSG/SEVIRI with in situ measurements at Gobabeb, Namibia. Int. J. Remote Sens. 2013, 34, 3069–3083. [Google Scholar] [CrossRef]
- Freitas, S.C.; Trigo, I.F.; Bioucas-Dias, J.M.; Göttsche, F.-M. Quantifying the uncertainty of land surface temperature retrievals from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2010, 48, 523–534. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Biard, J.; Hulley, G.C.; Privette, J.L.; Hook, S.J.; Olioso, A.; Göttsche, F.-M.; Radocinski, R.; Román, M.O.; Yu, Y.; et al. Validation of land surface temperature products derived from the Visible Infrared Imager Radiometer Suite (VIIRS) using ground-based and heritage satellite measurements. Remote Sens. Environ. 2014, 154, 19–37. [Google Scholar] [CrossRef]
- Li, H.; Sun, D.; Yu, Y.; Wang, H.; Liu, Y.; Liu, Q.; Du, Y.; Wang, H.; Cao, B. Evaluation of the VIIRS and MODIS LST products in an arid area of Northwest China. Remote Sensing of Environment 2014, 142, 111–121. [Google Scholar] [CrossRef]
- Barnes, W.L.; Pagano, T.S.; Salomonson, V.V. Prelaunch characteristics of the Moderate Resolution Imaging Spectroradiometer (MODIS) on EOS-AM1. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1088–1100. [Google Scholar] [CrossRef]
- Level 1, the Atmosphere Archive and Distribution System (LAADS). Available online: http://ladsweb.nascom.nasa.gov/data/search.html (accessed on 19 March 2015).
- NASA-developed EOS Clearinghouse (ECHO). Available online: http://wist.echo.nasa.gov/api (accessed on 19 March 2015).
- Snyder, W.C.; Wan, Z.; Zhang, Y.; Feng, Y.Z. Classification-based emissivity for land surface temperature measurement from space. Int. J. Remote Sens. 1998, 19, 2753–2774. [Google Scholar] [CrossRef]
- Land Cover Type Yearly L3 Global 500 m SIN Grid. Available online: https://lpdaac.usgs.gov/products/modis_products_table/mcd12q1 (accessed on 19 March 2015).
- Sobrino, J.A.; Li, Z.-L.; Stoll, M.P.; Becker, F. Multi-channel and multi-angle algorithms for estimating sea and land surface temperature with ATSR data. Int. J. Remote Sens. 1996, 17, 2089–2114. [Google Scholar] [CrossRef]
- Li, Z.-L.; Petitcolin, F.; Zhang, R.H. A physically based algorithm for land surface emissivity retrieval from combined mid-infrared and thermal infrared data. Sci. China Ser. E: Technol. Sci. 2000, 43, 23–33. [Google Scholar] [CrossRef]
- McMillin, L.M. Estimation of sea surface temperature from two infrared window measurements with different absorptions. J. Geophys. Res. 1975, 80, 5113–5117. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.-L. Towards a local split window method over land surfaces. Int. J. Remote Sens. 1990, 11, 369–393. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V.; Sobrino, J.A.; Valor, E. On the atmospheric dependence of the split-window equation for land surface temperature. Int. J. Remote Sens. 1994, 15, 105–122. [Google Scholar] [CrossRef]
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN cloud and multiple scattering upgrades with application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
- Thermodynamic Initial Guess Retrieval (TIGR). Available online: http://ara.abct.lmd.polytechnique.fr/index.php?page=tigr (accessed on 19 March 2015).
- Platt, C.M.R.; Prata, A.J. Nocturnal effects in the retrieval of land surface temperature from satellite measurements. Remote Sens. Environ. 1993, 45, 127–136. [Google Scholar] [CrossRef]
- MODIS UCSB Emissivity Library. Available online: http://www.icess.ucsb.edu/modis/EMIS/html/em.html (accessed on 19 March 2015).
- The Johns Hopkins University (JHU) spectral database. Available online: http://speclib.jpl.nasa.gov/ (accessed on 19 March 2015).
- Coll, C.; Caselles, V. A split-window algorithm for land surface temperature from advanced very high resolution radiometer data: Validation and algorithm comparison. J. Geophys. Res. 1997, 102, 16697–16713. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: Application to Morocco. Int. J. Remote Sens. 2000, 21, 353–366. [Google Scholar] [CrossRef]
- Soria, G.; Sobrino, J.A. ENVISAT/AATSR derived land surface temperature over a heterogeneous region. Remote Sens. Environ. 2007, 111, 409–422. [Google Scholar] [CrossRef]
- Prata, A.J.; Caselles, V.; Colland, C.; Sobrino, J.A.; Ottle, C. Thermal remote sensing of land surface temperature from satellites: Current status and future prospects. Remote Sens. Rev. 1995, 12, 175–224. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Caselles, V.; Coll, C. Theoretical split-window algorithms for determining the actual surface temperature. IL Nuovo Cimento C 1993, 16, 219–236. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Li, Z.-L.; Jia, L.; Su, Z.; Wan, Z.; Zhang, R. A new approach for retrieving precipitable water from ATSR2 split-window channel data over land area. Int. J. Remote Sens. 2003, 24, 5095–5117. [Google Scholar] [CrossRef]
- MODIS Reprojection Tool. Available online: https://lpdaac.usgs.gov/tools/modis_reprojection_tool (accessed on 19 March 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, B.-H.; Shao, K.; Li, Z.-L.; Wu, H.; Nerry, F.; Zhou, G. Estimation and Validation of Land Surface Temperatures from Chinese Second-Generation Polar-Orbit FY-3A VIRR Data. Remote Sens. 2015, 7, 3250-3273. https://doi.org/10.3390/rs70303250
Tang B-H, Shao K, Li Z-L, Wu H, Nerry F, Zhou G. Estimation and Validation of Land Surface Temperatures from Chinese Second-Generation Polar-Orbit FY-3A VIRR Data. Remote Sensing. 2015; 7(3):3250-3273. https://doi.org/10.3390/rs70303250
Chicago/Turabian StyleTang, Bo-Hui, Kun Shao, Zhao-Liang Li, Hua Wu, Françoise Nerry, and Guoqing Zhou. 2015. "Estimation and Validation of Land Surface Temperatures from Chinese Second-Generation Polar-Orbit FY-3A VIRR Data" Remote Sensing 7, no. 3: 3250-3273. https://doi.org/10.3390/rs70303250
APA StyleTang, B. -H., Shao, K., Li, Z. -L., Wu, H., Nerry, F., & Zhou, G. (2015). Estimation and Validation of Land Surface Temperatures from Chinese Second-Generation Polar-Orbit FY-3A VIRR Data. Remote Sensing, 7(3), 3250-3273. https://doi.org/10.3390/rs70303250