Inter-Comparison of High-Resolution Satellite Precipitation Products over Central Asia
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area

2.2. Datasets
2.2.1. Ground Reference Dataset
2.2.2. Satellite-Based Precipitation Dataset
| Name | Temporal Resolution | Spatial Resolution | Domain | Corrected by Gauges | Reference |
|---|---|---|---|---|---|
| 3B42RTV7 | 3 hr | 0.25° | 60°S–60°N | No | [24] |
| 3B42V7 | 3 hr | 0.25° | 50°S–50°N | Yes | [24] |
| CMORPH-RAW | 1 day | 0.25° | 60°S–60°N | No | [17] |
| CMORPH-CRT | 1 day | 0.25° | 60°S–60°N | Yes | [25] |
| GSMaP-MVK | 1 hr | 0.1° | 60°S–60°N | No | [22,23] |
| GSMaP-Gauge | 1 hr | 0.1° | 60°S–60°N | Yes | [22,23,27] |
| PERSIANN-RAW | 3 hr | 0.25° | 60°S–60°N | No | [18,19] |
| PERSIANN-CDR | 1 day | 0.25° | 60°S–60°N | Yes | [18,19,26] |
2.3. Statistical Evaluation Metrics
| Gauge ≥ Threshold | Gauge < Threshold | |
|---|---|---|
| QPE ≥ threshold | H | F |
| QPE < threshold | M | Z |
3. Results and Discussion
3.1. Three Year Daily Mean Precipitation


3.2. Seasonal Daily Mean Precipitation


3.3. Time Series Monthly Precipitation

3.4. Probability Distribution by Occurrence

3.5. Contingency Statistics

3.6. Spatial Analysis


4. Conclusions
- (1)
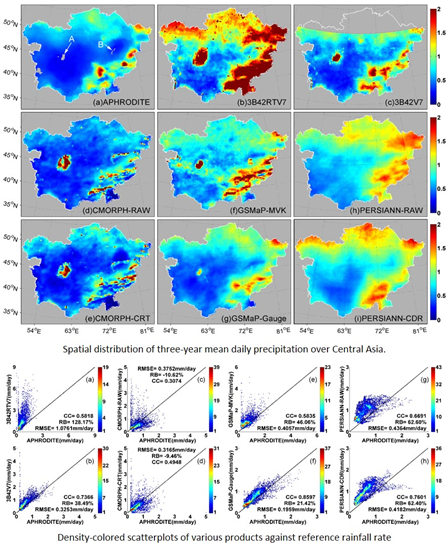
- Overall, the bias-correction procedures successfully decrease error of four groups of satellite-based precipitation products. The effectiveness of improvement varies for different bias-correction algorithms during 2004–2006 over Central Asia. The gauge-correction procedures in TMPA and GSMaP perform better with the reduction of RBs (from 128.17% to 38.49% and from 46.06% to 21.42%, respectively), RMSEs (from 1.08 to 0.33 mm/day and from 0.41 to 0.20 mm/day, respectively) and a dramatic increase in CCs (from 0.58 to 0.74 and from 0.58 to 0.86, respectively). On the other side, the bias correction could not bring significant change for CMORPH and PERSIANN products (for RBs from –10.62% to –9.46% and from 62.60% to 62.40%, respectively), and for RMSEs from 0.38 to 0.32 mm/day and from 0.44 to 0.42 mm/day, respectively. However, the improvement in CC shows from 0.31 to 0.49 and 0.67 to 0.76, respectively. The gauge-correction procedure in GSMaP exhibits best performance in improving CC and reducing various errors, such as regional errors, near-big-lake overestimation, mountainous error, season-dependent error.
- (2)
- Qualitatively, all the satellite-based QPE products present overestimation or underestimation over southeastern Central Asia with high altitude, although these mountainous errors are largely reduced by different bias-correction techniques. Furthermore, all the PMW-based satellite-based precipitation products (i.e., 3B42RTV7 and 3B42V7, CMORPH_RAW and CMORPH_CRT, GSMaP_MVK and GSMaP_Gauge) overestimate much precipitation over the near-big-lake areas (e.g. Arial Sea and surrounding regions), while the IR-based PERSIANN products avoid this overestimation problem caused by large water bodies. This result provides additional support for the hypothesis of Tian et al. [89] that the PMW algorithms over land are affected by the small inland water bodies. In addition, these kinds of problems also existed in large inland water bodies. Therefore, satellite-based precipitation algorithms need to be improved further by developing screening strategies to discriminate land pixels and with false rainfall signatures (water bodies, snow or ice surface and complicated mountains) for the accurate estimation of precipitation over regions near large water bodies, areas covered by ice or snow and mountainous areas.
- (3)
- For the three-year daily mean precipitation, all the eight satellite products are capable of capturing the overall spatial pattern of precipitation (Figure 2 and Figure 3). Among the four satellite-only QPE products, 3B42RTV7 demonstrates the poorest performance with the largest magnitude of RB (128.17%) and RMSE (1.08 mm/day). PERSIANN_RAW exhibits the highest CC (0.67), but relatively high RB and RMSE (62.60% and 0.44 mm/day, respectively). In the comparison of bias-corrected satellite products, GSMaP_Gauge represents the highest CC (0.86) and smallest RMSE (0.20 mm/day), as well as low RB (21.42%) over Central Asia compared to other bias-corrected products.
- (4)
- Seasonally, both gauge-corrected and the original satellite QPE products give best (worst) performance with the highest (lowest) CC, but relatively high RB and RMSE in summer (winter) as shown in Figure 4 and Figure 5. The RMSEs of satellite-only products remains more than 0.66 mm/day and CC less than 0.28 in winter. 3B42RTV7 shows significant overestimation with RB more than 108.81% and RMSE more than 0.89 mm/day, although these conditions are much improved with RB less than 46.64% and RMSE less than 0.50 mm/day in 3B42V7.
- (5)
- Gauge-calibrated products give quite different performance in the monthly series of behavior due to different bias-correction algorithms (Figure 6). 3B42V7 displays a consistent slight Bias and RMSE but relatively reversed season-dependent CC fluctuated from ~0.3 in cold seasons to ~0.85 in warm seasons. Bias-correction technique in CMORPH_CRT cannot perform well over semi-arid and arid areas in improving CC, removing bias and decreasing season-dependent variability. GSMaP_Gauge exhibits the best correlation against APHRODITE with high and stable CC over ~0.7 but cannot reduce Bias and RMSE significantly. PERSIANN_CDR gives an overestimation consistently with a CC (>0.55) and small RMSE (<0.8) over Central Asia during 2004–2006.
- (6)
- All the satellite original precipitation products, as well as bias-corrected 3B42V7 and CMORPH_CRT, tend to detect much more non-rain events than the ground measurements, while GSMaP_Gauge and PERSIANN_CDR display similar non-rain events, with under-detection of about 1% and 2%, respectively. 3B42RTV7 and CMORPH over-detect non-rain occurrence with values more than 75% while their corresponding bias-corrected counterparts (3B42V7 and CMORPH_CRT) detect even more occurrence of no rain. GSMaP_Gauge gives the closest percentage of non-rain with APHRODITE. All products detect less precipitating days than the reference dataset at the light rain range (0–1 mm/day) and detect moderate precipitation events over 2 mm/day. GSMaP_Gauge (PERSIANN_CDR) demonstrates the closest PDF with APHRODITE in the range of 0 to 10 mm/day (more than 10 mm/day). It is noted that all QPE products except GSMaP_Gauge show similar low POD and CSI pattern, and GSMaP_Gauge outperforms other products with higher POD and CSI. PERSIANN_CDR, GSMaP_Gauge and 3B42V7 show the lowest FAR percent during 0.1–2 mm/day, 2–18 mm/day, and 18–40 mm/day, respectively.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Karaseva, M.; Prakash, S.; Gairola, R.M. Validation of high-resolution TRMM-3B43 precipitation product using rain gauge measurements over Kyrgyzstan. Theor. Appl. Climatol. 2012, 108, 147–157. [Google Scholar] [CrossRef]
- Habib, E.; Haile, A.T.; Tian, Y.; Joyce, R.J. Evaluation of the high-resolution cmorph satellite rainfall product using dense rain gauge observations and radar-based estimates. J. Hydrometeorol. 2012, 13, 1784–1798. [Google Scholar] [CrossRef]
- Hong, Y.; Adler, R.; Huffman, G. Evaluation of the potential of NASA multi-satellite precipitation analysis in global landslide hazard assessment. Geophys. Res. Lett. 2006, 33, L22402. [Google Scholar] [CrossRef]
- Aragão, L.E.O.C.; Malhi, Y.; Roman-Cuesta, R.M.; Saatchi, S.; Anderson, L.O.; Shimabukuro, Y.E. Spatial patterns and fire response of recent Amazonian droughts. Geophys. Res. Lett. 2007, 34, L07701. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Hong, Y.; Tian, Y.; Policelli, F. Evaluation of global flood detection using satellite-based rainfall and a hydrologic model. J. Hydrometeorol. 2012, 13, 1268–1284. [Google Scholar] [CrossRef]
- Xie, P.; Arkin, P.A. An intercomparison of gauge observations and satellite estimates of monthly precipitation. J. Appl. Meteorol. 1995, 34, 1143–1160. [Google Scholar] [CrossRef]
- Xie, P.; Arkin, P.A. Analyses of global monthly precipitation using gauge observations, satellite estimates, and numerical model predictions. J. Clim. 1996, 9, 840–858. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Maggioni, V.; Nikolopoulos, E.I.; Meskele, T.; Hossain, F.; Papadopoulos, A. Benchmarking high-resolution global satellite rainfall products to radar and rain-gauge rainfall estimates. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1667–1683. [Google Scholar] [CrossRef]
- Ciach, G.J.; Krajewski, W.F.; Villarini, G. Product-error-driven uncertainty model for probabilistic quantitative precipitation estimation with NEXRAD data. J. Hydrometeorol. 2007, 8, 1325–1347. [Google Scholar] [CrossRef]
- Germann, U.; Galli, G.; Boscacci, M.; Bolliger, M. Radar precipitation measurement in a mountainous region. Q. J. R. Meteorol. Soc. 2006, 132, 1669–1692. [Google Scholar] [CrossRef]
- Piccolo, F.; Chirico, G.B. Sampling errors in rainfall measurements by weather radar. Adv. Geosci. 2005, 2, 151–155. [Google Scholar] [CrossRef]
- Anagnostou, E. Overview of overland satellite rainfall estimation for hydro-meteorological applications. Surv. Geophys. 2004, 25, 511–537. [Google Scholar] [CrossRef]
- Sharif, H.O.; Ogden, F.L.; Krajewski, W.F.; Xue, M. Numerical simulations of radar rainfall error propagation. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Chen, S.; Gourley, J.J.; Hong, Y.; Kirstetter, P.E.; Zhang, J.; Howard, K.; Flamig, Z.L.; Hu, J.; Qi, Y. Evaluation and uncertainty estimation of NOAA/NSSL next-generation national mosaic quantitative precipitation estimation product (Q2) over the continental United States. J. Hydrometeorol. 2013, 14, 1308–1322. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q. Inter-comparison of precipitation estimates from WSR-88D radar and TRMM measurement over continental United States. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4444–4456. [Google Scholar]
- Chen, S.; Hong, Y.; Cao, Q.; Kirstetter, P.-E.; Gourley, J.J.; Qi, Y.; Zhang, J.; Howard, K.; Hu, J.; Wang, J. Performance evaluation of radar and satellite rainfalls for typhoon Morakot over Taiwan: Are remote-sensing products ready for gauge denial scenario of extreme events? J. Hydrol. 2013, 506, 4–13. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. Cmorph: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN system satellite-based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Hsu, K.-L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.-L.; Sorooshian, S.; Gao, X. Precipitation estimation from remotely sensed imagery using an artificial neural network cloud classification system. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef]
- Turk, F.J.; Arkin, P.; Sapiano, M.R.P.; Ebert, E.E. Evaluating high-resolution precipitation products. Bull. Am. Meteorol. Soc. 2008, 89, 1911–1916. [Google Scholar] [CrossRef]
- Okamoto, K.; Ushio, T.; Iguchi, T.; Takahashi, N.; Iwanami, K. The global satellite mapping of precipitation (GSMaP) project. In Proceedings of 2005 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2005), Seoul, Korea, 25–29 July 2005; pp. 3414–3416.
- Kubota, T.; Shige, S.; Hashizurne, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global precipitation map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.J.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Xie, P.; Yoo, S.-H.; Joyce, R.; Yarosh, Y. Bias-corrected CMORPH: A 13-year analysis of high-resolution global precipitation. Availeble online: http://ftp.cpc.ncep.noaa.gov/precip/CMORPH_V1.0/REF/EGU_11462 (accessed on 11 December 2014).
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multi-satellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2014, 96, 69–83. [Google Scholar] [CrossRef]
- Mega, T.; Ushio, T.; Kubota, T.; Kachi, M.; Aonashi, K.; Shige, S. Gauge adjusted global satellite mapping of precipitation (GSMaP_Gauge). In Proceedings of 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; pp. 1–4.
- Aonashi, K.; Shibata, A.; Liu, G. An over-ocean precipitation retrieval using SSM/I multichannel brightness temperatures. J. Meteorol. Soc. Jpn. 1996, 74, 617–637. [Google Scholar]
- Shrestha, M.S.; Artan, G.A.; Bajracharya, S.R.; Gautam, D.K.; Tokar, S.A. Bias-adjusted satellite-based rainfall estimates for predicting floods: Narayani basin. J. Flood Risk Manag. 2011, 4, 360–373. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Assessment of satellite rainfall products for streamflow simulation in medium watersheds of the Ethiopian highlands. Hydrol. Earth Syst. Sci. 2011, 15, 1147–1155. [Google Scholar] [CrossRef]
- Nikolopoulos, E.; Anagnostou, E.; Hossain, F. Error propagation of satellite-rainfall in flood prediction applications over complex terrain: A case study in northeastern Italy. In Satellite rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer: Dordrecht, The Nederlands, 2010; pp. 215–227. [Google Scholar]
- Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based multi-satellite precipitation analysis over the Wangchu basin of Bhutan: Are the latest satellite precipitation products 3B42V7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; You, Y.; Mullens, E.; Hu, J.; Yuan, Y.; Huang, M.; He, L.; Luo, Y.; Zeng, X.; et al. Evaluation of high-resolution precipitation estimates from satellites during July 2012 Beijing flood event using dense rain gauge observations. PLoS ONE 2014, 9, e89681. [Google Scholar] [CrossRef] [PubMed]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the version-6 and version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar]
- Stisen, S.; Sandholt, I. Evaluation of remote-sensing-based rainfall products through predictive capability in hydrological runoff modelling. Hydrol. Process. 2010, 24, 879–891. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.-L.; Moradkhani, H.; Sorooshian, S. Uncertainty quantification of satellite precipitation estimation and Monte Carlo assessment of the error propagation into hydrologic response. Water Resour. Res. 2006, 42, W08421. [Google Scholar] [CrossRef]
- Sorooshian, S.; AghaKouchak, A.; Arkin, P.; Eylander, J.; Foufoula-Georgiou, E.; Harmon, R.; Hendrickx, J.M.H.; Imam, B.; Kuligowski, R.; Skahill, B.; et al. Advanced concepts on remote sensing of precipitation at multiple scales. Bull. Am. Meteorol. Soc. 2011, 92, 1353–1357. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Mehran, A.; Norouzi, H.; Behrangi, A. Systematic and random error components in satellite precipitation data sets. Geophys. Res. Lett. 2012, 39, L09406. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.-L.; Turk, F.J.; Garcia, M.; Zeng, J. Component analysis of errors in satellite-based precipitation estimates. J. Geophys. Res.: Atmos. 2009, 114, D24101. [Google Scholar] [CrossRef]
- Mehran, A.; AghaKouchak, A. Capabilities of satellite precipitation datasets to estimate heavy precipitation rates at different temporal accumulations. Hydrol. Process. 2014, 28, 2262–2270. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Gebremichael, M.; Hopson, T. Evaluation of high-resolution satellite precipitation products over very complex terrain in Ethiopia. J. Appl. Meteorol. Climatol. 2010, 49, 1044–1051. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Hong, Y.; Yong, B.; Yang, X.; Yuan, F.; Ma, M. Comprehensive evaluation of multi-satellite precipitation products with a dense rain gauge network and optimally merging their simulated hydrological flows using the Bayesian model averaging method. J. Hydrol. 2012, 452–453, 213–225. [Google Scholar] [CrossRef]
- Dinku, T.; Ruiz, F.; Connor, S.J.; Ceccato, P. Validation and intercomparison of satellite rainfall estimates over Colombia. J. Appl. Meteorol. Climatol. 2009, 49, 1004–1014. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Hossain, F. Understanding the dependency of satellite rainfall uncertainty on topography and climate for hydrologic model simulation. IEEE Trans. Geosci. Remote Sens. 2011, 51, 704–718. [Google Scholar] [CrossRef]
- Sapiano, M.R.P.; Arkin, P.A. An intercomparison and validation of high-resolution satellite precipitation estimates with 3-hourly gauge data. J. Hydrometeorol. 2009, 10, 149–166. [Google Scholar] [CrossRef]
- Wei, C.-C.; Roan, J. Retrievals for the rainfall rate over land using special sensor microwave imager data during tropical cyclones: Comparisons of scattering index, regression, and support vector regression. J. Hydrometeorol. 2012, 13, 1567–1578. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Evaluation through independent measurements: Complex terrain and humid tropical region in Ethiopia. In Satellite Rainfall Applications for Surface Hydrology; Springer Netherlands: Berlin, Germany, 2010; pp. 205–214. [Google Scholar]
- Romilly, T.G.; Gebremichael, M. Evaluation of satellite rainfall estimates over Ethiopian river basins. Hydrol. Earth Syst. Sci. 2011, 15, 1505–1514. [Google Scholar] [CrossRef]
- Hsu, K.-L.; Sorooshian, S. Satellite-based precipitation measurement using Persiann system. In Hydrological Modelling and the Water Cycle; Sorooshian, S., Hsu, K.-L., Coppola, E., Tomassetti, B., Verdecchia, M., Visconti, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 63, pp. 27–48. [Google Scholar]
- Yamamoto, K.M.; Ueno, K.; Nakamura, K. Comparison of satellite precipitation products with rain gauge data for the Khumb region, Nepal Himalayas. J. Meteorol. Soc. Jan. Ser. II 2011, 89, 597–610. [Google Scholar] [CrossRef]
- Kubota, T.; Ushio, T.; Shige, S.; Kida, S.; Kachi, M.; Okamoto, K.I. Verification of high-resolution satellite-based rainfall estimates around Japan using a gauge-calibrated ground-radar dataset. J. Meteorol. Soc. Jan. Ser. II 2009, 87A, 203–222. [Google Scholar] [CrossRef]
- Ngo-Duc, T.; Matsumoto, J.; Kamimera, H.; Bui, H.-H. Monthly adjustment of global satellite mapping of precipitation (GSMaP) data over the VuGia-ThuBon river basin in central Vietnam using an artificial neural network. Hydrol. Res. Lett. 2013, 7, 85–90. [Google Scholar] [CrossRef]
- Shrestha, M.; Takara, K.; Kubota, T.; Bajracharya, S. Verification of GSMaP rainfall estimates over the central Himalayas. J. Jan. Soc. Civil Eng., Ser. B1 (Hydraul. Eng.) 2011, 67. [Google Scholar] [CrossRef]
- Taniguchi, A.; Shige, S.; Yamamoto, M.K.; Mega, T.; Kida, S.; Kubota, T.; Kachi, M.; Ushio, T.; Aonashi, K. Improvement of high-resolution satellite rainfall product for typhoon Morakot (2009) over Taiwan. J. Hydrometeorol. 2013, 14, 1859–1871. [Google Scholar] [CrossRef]
- Tian, Y.D.; Peters-Lidard, C.D.; Adler, R.F.; Kubota, T.; Ushio, T. Evaluation of GSMaP precipitation estimates over the contiguous united states. J. Hydrometeorol. 2010, 11, 566–574. [Google Scholar] [CrossRef]
- Ushio, T.; Sasashige, K.; Kubota, T.; Shige, S.; Okamoto, K.I.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M.; et al. A kalman filter approach to the global satellite mapping of precipitation (GSMaP) from combined passive microwave and infrared radiometric data. J. Meteorol. Soc. Jan. Ser. II 2009, 87, 137–151. [Google Scholar] [CrossRef]
- Veerakachen, W.; Raksapatcharawong, M.; Seto, S. Performance evaluation of global satellite mapping of precipitation (GSMaP) products over the Chaophraya river basin, Thailand. Hydrol. Res. Lett. 2014, 8, 39–44. [Google Scholar] [CrossRef]
- Baopu, F. The effects of orography on precipitation. Bound-Lay Meteorol. 1995, 75, 189–205. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Hossain, F. How well can we estimate error variance of satellite precipitation data across the world? . Atmos. Res. 2015, 154, 39–59. [Google Scholar] [CrossRef]
- Mughal, M.A.Z. Pamir alpine desert and tundra. In Biomes and Ecosystems; Warren Howarth, R., Ed.; Salem Press: Ipswich, MA, USA, 2013; Volume 3, pp. 978–980. [Google Scholar]
- Schiemann, R.; Lüthi, D.; Vidale, P.L.; Schär, C. The precipitation climate of central Asia—Intercomparison of observational and numerical data sources in a remote semiarid region. Int. J. Climatol. 2008, 28, 295–314. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM National Conference; ACM: New York, NY, USA, 1968; pp. 517–524. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Smart interpolation of annually averaged air temperature in the United States. J. Appl. Meteorol. 1995, 34, 2577–2586. [Google Scholar] [CrossRef]
- Schaake, J.; Henkel, A.; Cong, S. Application of PRISM climatologies for hydrologic modeling and forecasting in the western U.S. In Proceedings of 18th Conference on Hydrology, Seattle, WA, USA, 15 January 2004.
- Rajeevan, M.; Bhate, J. A high resolution daily gridded rainfall dataset (1971–2005) for mesoscale meteorological studies. Curr. Sci. India 2009, 96, 558–562. [Google Scholar]
- Yatagai, A.; Xie, P. Utilization of a rain-gauge-based daily precipitation dataset over Asia for validation of precipitation derived from TRMM/PR and JRA-25. Proc. SPIE 2006. [Google Scholar] [CrossRef]
- Yatagai, A.; Arakawa, O.; Kamiguchi, K.; Kawamoto, H.; Nodzu, M.I.; Hamada, A. A 44-year daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Sola 2009, 5, 137–140. [Google Scholar] [CrossRef]
- Yatagai, A.; Xie, P.; Kitoh, A. Utilization of a new gauge-based daily precipitation dataset over monsoon Asia for validation of the daily precipitation climatology simulated by the MRI/JMA 20-km-mesh AGCM. Sola 2005, 1, 193–196. [Google Scholar] [CrossRef]
- Andermann, C.; Bonnet, S.; Gloaguen, R. Evaluation of precipitation data sets along the Himalayan front. Geochem. Geophys. Geosyst. 2011, 12, Q07023. [Google Scholar] [CrossRef]
- Shrivastava, R.; Dash, S.K.; Hegde, M.N.; Pradeepkumar, K.S.; Sharma, D.N. Validation of the TRMM multi satellite rainfall product 3B42 and estimation of scavenging coefficients for 131I and 137Cs using TRMM 3B42 rainfall data. J. Environ. Radioact. 2014, 138, 132–136. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kang, B.; Adams, J.M. Opposite trends in summer precipitation in South and North Korea. Int. J. Climatol. 2012, 32, 2311–2319. [Google Scholar] [CrossRef]
- Raziei, T.; Bordi, I.; Santos, J.A.; Mofidi, A. Atmospheric circulation types and winter daily precipitation in Iran. Int. J. Climatol. 2013, 33, 2232–2246. [Google Scholar] [CrossRef]
- Raziei, T.; Mofidi, A.; Santos, J.A.; Bordi, I. Spatial patterns and regimes of daily precipitation in Iran in relation to large-scale atmospheric circulation. Int. J. Climatol. 2012, 32, 1226–1237. [Google Scholar] [CrossRef]
- Andermann, C.; Longuevergne, L.; Bonnet, S.; Crave, A.; Davy, P.; Gloaguen, R. Impact of transient groundwater storage on the discharge of Himalayan rivers. Nature Geosci. 2012, 5, 127–132. [Google Scholar] [CrossRef] [Green Version]
- Mishra, V.; Kumar, D.; Ganguly, A.R.; Sanjay, J.; Mujumdar, M.; Krishnan, R.; Shah, R.D. Reliability of regional and global climate models to simulate precipitation extremes over India. J. Geophys. Res.: Atmos. 2014, 119, 9301–9323. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. Aphrodite: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Joyce, R.J.; Xie, P. Kalman filter-based CMORPH. J. Hydrometeorol. 2011, 12, 1547–1563. [Google Scholar] [CrossRef]
- Seto, S.; Takahashi, N.; Iguchi, T. Rain/no-rain classification methods for microwave radiometer observations over land using statistical information for brightness temperatures under no-rain conditions. J. Appl. Meteorol. 2005, 44, 1243–1259. [Google Scholar] [CrossRef]
- Takahashi, N.; Awaka, J. Introduction of a melting layer model to a rain retrieval algorithm for microwave radiometers. IEEE Int. Geosci. Remote Sens. Symp. 2005, 5, 3404–3409. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Amsterdam, Boston, USA, 2011; Volume 100, p. 676. [Google Scholar]
- Tesfagiorgis, K.; Mahani, S.E.; Khanbilvardi, R. Bias correction of satellite rainfall estimation using a radar-gauge product. Hydrol. Earth Syst. Sci. Discuss. 2010, 7, 8913–8945. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Gourley, J.J.; Kirstetter, P.E.; Yong, B.; Tian, Y.; Zhang, Z.; Shen, Y.; Hu, J. Similarity and difference of the two successive V6 and V7 TRMM multisatellite precipitation analysis performance over China. J. Geophys. Res.: Atmos. 2013, 118, 13060–13074. [Google Scholar] [CrossRef]
- Story, G.J.; Forecaster, H.; Center, W.G.R.F. Determining WSR-88D Precipitation Algorithm Performance Using the Stage III Precipitation Processing System. Available online: http://ftp.hydro.washington.edu/pub/lettenma/cee_599/radar_precipitation/Determining%20WSR-88D%20Precation%20Processing%20System.pdf (accessed on 4 November 2014).
- Surussavadee, C.; Staelin, D.H. Correcting microwave precipitation retrievals for near-surface evaporation. In Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 1312–1315.
- Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal analysis of TRMM-based satellite precipitation products for land data assimilation applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
- Grody, N.C.; Weng, F. Microwave emission and scattering from deserts: Theory compared with satellite measurements. IEEE Trans. Geosci. Remote Sens. 2008, 46, 361–375. [Google Scholar] [CrossRef]
- Yang, Y.; Luo, Y. Evaluating the performance of remote sensing precipitation products CMORPH, PERSIANN, and TMPA, in the arid region of Northwest China. Theor. Appl. Climatol. 2014, 118, 429–445. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D. Systematic anomalies over inland water bodies in satellite-based precipitation estimates. Geophys Res. Lett. 2007, 34, L14403. [Google Scholar] [CrossRef]
- Xie, P.; Chen, M.; Yang, S.; Yatagai, A.; Hayasaka, T.; Fukushima, Y.; Liu, C. A gauge-based analysis of daily precipitation over East Asia. J. Hydrometeorol. 2007, 8, 607–626. [Google Scholar] [CrossRef]
- Chen, M.; Shi, W.; Xie, P.; Silva, V.B.S.; Kousky, V.E.; Wayne Higgins, R.; Janowiak, J.E. Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res.: Atmos. 2008, 113, D04110. [Google Scholar]
- Li, Z.; Yang, D.W.; Hong, Y. Multi-scale evaluation of high-resolution multi-sensor blended global precipitation products over the Yangtze River. J. Hydrol. 2013, 500, 157–169. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res.: Atmos. 2010, 115, D02114. [Google Scholar] [CrossRef]
- Gosset, M.; Viarre, J.; Quantin, G.; Alcoba, M. Evaluation of several rainfall products used for hydrological applications over West Africa using two high-resolution gauge networks. Q. J. R. Meteorol. Soc. 2013, 139, 923–940. [Google Scholar] [CrossRef]
- Behrangi, A.; Tian, Y.; Lambrigtsen, B.H.; Stephens, G.L. What does CloudSat reveal about global land precipitation detection by other spaceborne sensors? Water Resour. Res. 2014, 50, 4893–4905. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, S.; Cao, Q.; Hong, Y.; Wu, B.; Huang, M.; Qiao, L.; Zhang, Z.; Li, Z.; Li, W.; et al. Evaluation of version-7 TRMM multi-satellite precipitation analysis product during the Beijing extreme heavy rainfall event of 21 July 2012. Water 2013, 6, 32–44. [Google Scholar] [CrossRef]
- Aonashi, K.; Liu, G. Passive microwave precipitation retrievals using TMI during the BAIU period of 1998. Part I: Algorithm description and validation. J. Appl. Meteorol. 2000, 39, 2024–2037. [Google Scholar]
- Bohren, C.F.; Battan, L.J. Radar backscattering by inhomogeneous precipitation particles. J. Atmos. Sci. 1980, 37, 1821–1827. [Google Scholar] [CrossRef]
- Lehning, M.; Löwe, H.; Ryser, M.; Raderschall, N. Inhomogeneous precipitation distribution and snow transport in steep terrain. Water Resour. Res. 2008, 44, W07404. [Google Scholar] [CrossRef]
- Smith, P.L.; Liu, Z.; Joss, J. A study of sampling-variability effects in raindrop size observations. J. Appl. Meteorol. 1993, 32, 1259–1269. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Chen, S.; Bao, A.; Hu, J.; Gebregiorgis, A.S.; Xue, X.; Zhang, X. Inter-Comparison of High-Resolution Satellite Precipitation Products over Central Asia. Remote Sens. 2015, 7, 7181-7211. https://doi.org/10.3390/rs70607181
Guo H, Chen S, Bao A, Hu J, Gebregiorgis AS, Xue X, Zhang X. Inter-Comparison of High-Resolution Satellite Precipitation Products over Central Asia. Remote Sensing. 2015; 7(6):7181-7211. https://doi.org/10.3390/rs70607181
Chicago/Turabian StyleGuo, Hao, Sheng Chen, Anming Bao, Jujun Hu, Abebe S. Gebregiorgis, Xianwu Xue, and Xinhua Zhang. 2015. "Inter-Comparison of High-Resolution Satellite Precipitation Products over Central Asia" Remote Sensing 7, no. 6: 7181-7211. https://doi.org/10.3390/rs70607181
APA StyleGuo, H., Chen, S., Bao, A., Hu, J., Gebregiorgis, A. S., Xue, X., & Zhang, X. (2015). Inter-Comparison of High-Resolution Satellite Precipitation Products over Central Asia. Remote Sensing, 7(6), 7181-7211. https://doi.org/10.3390/rs70607181