Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images
Abstract
:1. Introduction
2. Hyperspectral and Multispectral Image Fusion
2.1. Related Work
2.2. The CNMF Algorithm
3. Materials and Validation Methods
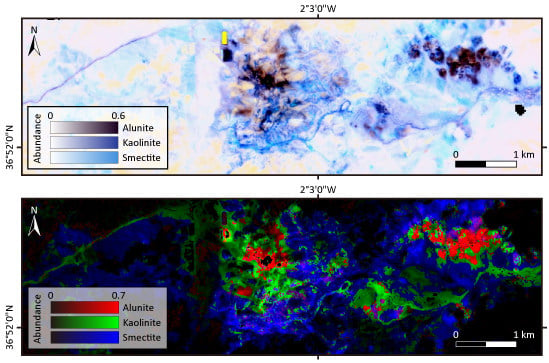
3.1. Study Area and Data Preparation
3.2. Validation Methods
- (1)
- CC is a characterization of geometric distortion obtained for each band with an ideal value of 1. We used an average value of CCs for all bands, which is defined as
- (2)
- SAM is a measure for the shape preservation of a spectrum calculated at each pixel with a unit degree and 0 as the ideal value. An average value of a whole image is defined aswhere denotes the column vector of X and ‖·‖ is the norm.
- (3)
- RMSE is calculated at each pixel as the difference of spectra between the fused image and the reference image. We used an average value of RMSEs for all pixels, which is defined as
- (4)
- ERGAS provides a global statistical measure of the quality of fused data with the best value at 0, which is defined as
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Goetz, A.F.H.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Vane, G.; Goetz, A.F.H. Terrestrial imaging spectrometry: Current status, future trends. Remote Sens. Environ. 1993, 44, 117–126. [Google Scholar] [CrossRef]
- Hunt, G.R. Spectral signatures of particulate minerals in the visible and near infrared. Geophysics 1977, 42, 501–513. [Google Scholar] [CrossRef] [Green Version]
- Clark, R.N.; Swayze, G.A.; Livo, K.E.; Kokaly, R.F.; Sutley, S.J.; Dalton, J.B.; Mcdougal, R.R.; Gent, C.A. Imaging spectroscopy: Earth and planetary remote sensing with the USGS Tetracorder and expert systems. J. Geophys. Res. Planets 2003, 108. [Google Scholar] [CrossRef]
- Kruse, F.A.; Boardman, J.W.; Huntington, J.F. Comparison of airborne hyperspectral data and EO-1 Hyperion for mineral mapping. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1388–1400. [Google Scholar] [CrossRef]
- Van der Meer, F.; Van der Werff, H.; Frank, J.A.; Van Ruitenbeek, F.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; van der Meijde, M.; Carranza, E.J.M.; Boudewijn de Smeth, J.; et al. Multi- and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Förster, S.; Rogaß, C.; Chabrillat, S.; Küster, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Pearlman, J.S.; Barry, P.S.; Segal, C.C.; Shepanski, J.; Beiso, D.; Carman, L. Hyperion, a space-based imaging spectrometer. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1160–1173. [Google Scholar] [CrossRef]
- Akgun, T.; Altunubasak, Y.; Mersereau, R.M. Super-resolution enhancement of hyperspectral CHRIS/Proba images with a thin-plate spline non-rigid transform model. IEEE Trans. Geosci. Remote Sens. 2005, 48, 1860–1875. [Google Scholar]
- Chan, J.C.-W.; Ma, J.; Kempeneers, P.; Canters, F. Superresolution reconstruction of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2005, 14, 2569–2579. [Google Scholar]
- Gu, Y.; Zhang, Y.; Zhang, J. Integration of spatial-spectral information for resolution enhancement in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1347–1358. [Google Scholar]
- Zhao, Y.; Zhang, L.; Kong, S.G. Band-subset-based clustering and fusion for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 747–756. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, M.; Licciardi, G. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Loncan, L.; Almeida, L.B.; Bioucas-Dias, J.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simoes, M.; et al. Hyperspectral pansharpening: A review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Hardie, R.C.; Eismann, M.T.; Wilson, G.L. MAP estimation for hyperspectral image resolution enhancement using an auxiliary sensor. IEEE Trans. Image Process. 2004, 13, 1174–1184. [Google Scholar] [CrossRef] [PubMed]
- Eismann, M.T.; Hardie, R.C. Application of the stochastic mixing model to hyperspectral resolution enhancement. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1924–1933. [Google Scholar] [CrossRef]
- Zhang, Y.; Backer, S.D.; Scheunders, P. Noise-resistant wavelet based Bayesian fusion of multispectral and hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3834–3843. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Kawakami, R.; Wright, J.; Tai, Y.; Matsushita, Y.; Ben-Ezra, M.; Ikeuchi, K. High-resolution hyperspectral imaging via matrix factorization. In Proceedings of the IEEE International Conference Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 21–23 June 2011; pp. 2329–2336.
- Veganzones, M.; Simes, M.; Licciardi Yokoya, N.; Bioucas-Dias, J.M.; Chanussot, J. Hyperspectral super-resolution of locally low rank images from complementary multisource data. IEEE Trans. Image Process. 2016, 25, 274–288. [Google Scholar] [CrossRef] [PubMed]
- Simoes, M.; Bioucas-Dias, J.M.; Almeida, L.; Chanussot, J. A convex formulation for hyperspectral image superresolution via subspace-based regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3373–3388. [Google Scholar] [CrossRef]
- Wei, Q.; Bioucas-Dias, J.M.; Dobigeon, N.; Tourneret, J.-Y. Hyperspectral and multispectral image fusion based on a sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef]
- Chen, Z.; Pu, H.; Wang, B.; Jiang, G.-M. Fusion of hyperspectral and multispectral images: A novel framework based on generalization of pan-sharpening methods. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1418–1422. [Google Scholar] [CrossRef]
- Grohnfeldt, C.; Zhu, X.; Bamler, R. The J-SparseFI-HM hyperspectral resolution enhancement method—Now fully automated. In Proceedings of the IEEE Workshop Hyperspectral Image Signal Process: Evolution in Remote Sens. (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; pp. 1–4.
- Van der Meer, F.D.; Van der Werff, H.M.A.; Van Ruitenbeek, F.J.A. Potential of ESA’s Sentinel-2 for geological applications. Remote Sens. Environ. 2014, 148, 124–133. [Google Scholar] [CrossRef]
- Guanter, L.; Segl, K.; Kaufmann, H. Simulation of optical remote sensing scenes with application to the EnMAP hyperspectral mission. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2340–2351. [Google Scholar] [CrossRef]
- Segl, K.; Guanter, L.; Kaufmann, H. Simulation of spatial sensor characteristics in the context of the EnMAP hyperspectral mission. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3046–3054. [Google Scholar] [CrossRef]
- Segl, K.; Guanter, L.; Rogass, C.; Kuester, T.; Roessner, S.; Kaufmann, H.; Sang, B.; Mogulsky, V.; Hofer, S. EeteS—The EnMAP end-to-end simulation tool. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2012, 5, 522–530. [Google Scholar] [CrossRef]
- Segl, K.; Guanter, L.; Gascon, F.; Kuester, T.; Rogass, C.; Mielke, C. S2eteS—An end-to-end modelling tool for the simulation of Sentinel-2 image products. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5560–5571. [Google Scholar] [CrossRef]
- Gomez, G.; Jazaeri, A.; Kafatos, M. Wavelet-based hyperspectral and multi-spectral image fusion. Proc. SPIE 2001. [Google Scholar] [CrossRef]
- Zhang, Y.; He, M. Multi-spectral and hyperspectral image fusion using 3-D wavelet transform. J. Electron. 2007, 24, 218–224. [Google Scholar] [CrossRef]
- Yokoya, N.; Mayumi, N.; Iwasaki, A. Cross-calibration for data fusion of EO-1/Hyperion and Terra/ASTER. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2013, 6, 419–426. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by nonnegative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [PubMed]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Proceedings of the Conference Advertising Neural Information Processing System, Vancouver, BC, Canada, 3–8 December 2001; Volume 13, pp. 556–562.
- Nascimento, J.M.P.; Bioucas-Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Bedini, E.; Van der Meer, F.; Van Ruitenbeek, F. Use of HyMap imaging spectrometer data to map mineralogy in the Rodalquilar caldera, southeast Spain. Int. J. Remote Sens. 2009, 30, 327–348. [Google Scholar] [CrossRef]
- Arribas, A.; Cunningham, C.G.; Rytuba, J.J.; Rye, R.O.; Kelly, W.C.; Podwysocki, M.H.; Mckee, E.H.; Tosdal, R.M. Geology, geochronology, fluid inclusions, and isotope geochemistry of the Rodalquilar gold alunite deposit, Spain. Econ. Geol. Bull. Soc. Econ. Geol. 1995, 90, 795–822. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS+Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Wald, L. Quality of high resolution synthesized images: Is there a simple criterion? In Proceedings of the Third Conference “Fusion of Earth Data”, Sophia Antipolis, France, 26–28 January 2000; pp. 99–105.
- Clark, R.N.; Gallagher, A.J.; Swayze, G.A. Material absorption band depth mapping of imaging spectrometer data using a complete band shape least-squares fit with library reference spectra. In Proceedings of the Second Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) Workshop, Pasadena, CA, USA, 4–5 June 1990; pp. 176–186.
- Singer, R.B. Near-infrared spectral reflectance of mineral mixtures: Systematic combinations of pyroxenes, olivine, and iron oxides. J. Geophys. Res. 1981, 86, 7967–7982. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy-quantitative analysis techniques for remote-sensing applications. J. Geophys. Res. 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modeling: A new analysis of rock and soil types at the Viking Lander 1 site. J. Geophys. Res. 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
- Roberts, D.A.; Gadner, M.; Church, R.; Ustin, S.; Scheer, G.; Green, O.R. Mapping chaparral in the Santa Monica mountains using multiple endmember spectral mixture models. Remote Sens. Environ. 1998, 65, 267–279. [Google Scholar] [CrossRef]
- Iwasaki, A.; Ohgi, N.; Tanii, J.; Kawashima, T.; Inada, H. Hyperspectral imager suite (HISUI)-Japanese hyper-multi spectral radiometer. In Proceedings of the International Geoscience Remote Sensing Symptom (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 1025–1028.
- Stefano, P.; Angelo, P.; Simone, P.; Filomena, R.; Federico, S.; Tiziana, S.; Umberto, A.; Vincenzo, C.; Acito, N.; Marco, D.; et al. The PRISMA hyperspectral mission: Science activities and opportunities for agriculture and land monitoring. In Proceedings of the International Geoscience Remote Sensing Symptom (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 4558–4561.
- Green, R.; Asner, G.; Ungar, S.; Knox, R. NASA mission to measure global plant physiology and functional types. In Proceedings of the Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; pp. 1–7.
- Michel, S.; Gamet, P.; Lefevre-Fonollosa, M.J. HYPXIM—A hyperspectral satellite defined for science, security and defence users. In Proceedings of the IEEE Workshop Hyperspectral Image Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011; pp. 1–4.
- Eckardt, A.; Horack, J.; Lehmann, F.; Krutz, D.; Drescher, J.; Whorton, M.; Soutullo, M. DESIS (DLR Earth sensing imaging spectrometer for the ISS-MUSES platform. In Proceedings of the International Geoscience Remote Sensing Symptom (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1457–1459.









| Band Number | Central Wavelength (nm) | Bandwidth (nm) | GSD (m) |
|---|---|---|---|
| 1 | 443 | 20 | 60 |
| 2 | 490 | 65 | 10 |
| 3 | 560 | 35 | 10 |
| 4 | 665 | 30 | 10 |
| 5 | 705 | 15 | 20 |
| 6 | 740 | 15 | 20 |
| 7 | 783 | 20 | 20 |
| 8 | 842 | 115 | 10 |
| 8b | 865 | 20 | 20 |
| 9 | 945 | 20 | 60 |
| 10 | 1380 | 30 | 60 |
| 11 | 1610 | 90 | 20 |
| 12 | 2190 | 180 | 20 |
| Data | Method | CC | SAM | RMSE | ERGAS |
|---|---|---|---|---|---|
| VNIR and SWIR | Cubic | 0.91749 | 2.8365 | 0.01909 | 3.3857 |
| GSA | 0.98629 | 2.713 | 0.01372 | 2.0112 | |
| MTF-GLP | 0.98571 | 2.692 | 0.01355 | 2.0151 | |
| CNMF | 0.988 | 2.6994 | 0.01349 | 1.9793 | |
| SWIR | Cubic | 0.90549 | 1.6368 | 0.01694 | 2.9814 |
| GSA | 0.97374 | 1.629 | 0.01149 | 1.9339 | |
| MTF-GLP | 0.97346 | 1.6381 | 0.01132 | 1.8958 | |
| CNMF | 0.97329 | 1.6193 | 0.01165 | 1.9336 | |
| Continuum removed SWIR | Cubic | 0.76578 | 0.65553 | 0.01015 | 0.45248 |
| GSA | 0.7745 | 0.64832 | 0.01011 | 0.4504 | |
| MTF-GLP | 0.7659 | 0.66141 | 0.01019 | 0.46186 | |
| CNMF | 0.83494 | 0.60761 | 0.00915 | 0.40899 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yokoya, N.; Chan, J.C.-W.; Segl, K. Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images. Remote Sens. 2016, 8, 172. https://doi.org/10.3390/rs8030172
Yokoya N, Chan JC-W, Segl K. Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images. Remote Sensing. 2016; 8(3):172. https://doi.org/10.3390/rs8030172
Chicago/Turabian StyleYokoya, Naoto, Jonathan Cheung-Wai Chan, and Karl Segl. 2016. "Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images" Remote Sensing 8, no. 3: 172. https://doi.org/10.3390/rs8030172
APA StyleYokoya, N., Chan, J. C. -W., & Segl, K. (2016). Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images. Remote Sensing, 8(3), 172. https://doi.org/10.3390/rs8030172