Estimating Evapotranspiration of an Apple Orchard Using a Remote Sensing-Based Soil Water Balance
Abstract
:1. Introduction
2. Materials and Methods
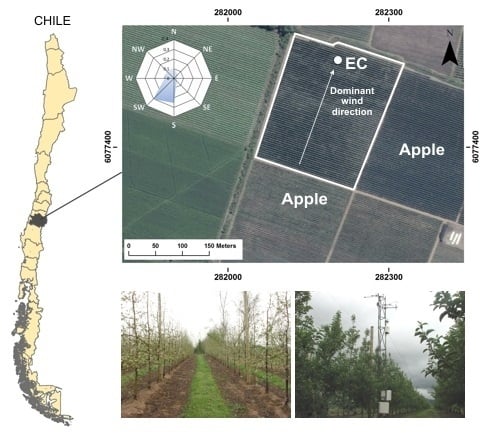
2.1. Site Description
2.2. Soil Water Balance Driven by Remote Sensing Data
2.2.1. Calculation of Satellite-Based Basal Crop Coefficient
2.2.2. Calculation of Soil Evaporation Coefficient
2.2.3. Estimation of Water Stress Coefficient
2.3. Soil Water Balance Parameterization
2.4. Experimental Data: EC Fluxes, Meteorological Data, Soil Moisture and Apple Water Status
2.5. Remote Sensing Data Acquisition and Processing
2.6. Statistical Analysis
3. Results and Discussion
3.1. Meteorological Conditions and Plant Water Status
3.2. Energy Balance Closure and Measured Values of ETc and Kc in the Apple Orchard
3.3. Seasonal Evolution of SAVI
3.4. Kcb Modeled from SAVI
3.5. Evaluation of the One Layer Soil Water Balance Model for Estimating ETc
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- ODEPA-CIREN. Catastro Frutícola. Principales Resultados. Región del Maule; Ministerio de Agricultura: Santiago, Chile, 2013; p. 48.
- Ministerio del Medio Ambiente. Segunda Comunicación Nacional de Chile ante la Convención Marco de las Naciones unidas sobre Cambio Climático; Ministerio del Medio Ambiente: Santiago, Chile, 2011; p. 289.
- Allen, R.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements; Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Doorenboos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements, Irrigation and Drainage Paper 24; Land and Water Development Division, FAO: Rome, Italy, 1977; p. 144. [Google Scholar]
- Wright, J.L. New evapotranspiration crop coefficients. J. Irrig. Drain. Div. 1982, 108, 57–74. [Google Scholar]
- Bausch, W.C. Remote sensing of crop coefficients for improving the irrigation scheduling of corn. Agric. Water Manag. 1995, 27, 55–68. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of ground cover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.U.; Calera, A.; Balbontín, C.; González-Piqueras, J. Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinifera L.). Agric. Water Manag. 2010, 98, 45–54. [Google Scholar] [CrossRef]
- Fereres, E.; Goldhamer, D.A. Deciduous Fruit and Nut Trees. In Irrigation of Agricultural Crops—Monogr. 30; Stewart, B.A., Nielsen, D.R., Eds.; ASA: Madison, WI, USA, 1990; pp. 987–1017. [Google Scholar]
- Bailey, R. Ecoclimatic zones of the earth. In Ecosystem Geography; Springer: New York, NY, USA, 2009; pp. 83–92. [Google Scholar]
- Massman, W.J. Reply to comment by rannik on “a simple method for estimating frequency response corrections for eddy covariance systems”. Agric. For. Meteorol. 2001, 107, 247–251. [Google Scholar] [CrossRef]
- Auzmendi, I.; Mata, M.; Lopez, G.; Girona, J.; Marsal, J. Intercepted radiation by apple canopy can be used as a basis for irrigation scheduling. Agric. Water Manag. 2011, 98, 886–892. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Fereres, E.; Raes, D. Crop yield response to water. In FAO Irrigation and Drainage Paper No. 66; FAO: Rome, Italy, 2012; p. 505. [Google Scholar]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Processes 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Bausch, W.C.; Neale, C.M.U. Crop coefficients derived from reflected canopy radiation: A concept. Trans. ASAE 1987, 30, 703–709. [Google Scholar] [CrossRef]
- Choudhury, B.; Ahmed, N.; Idso, S.; Reginato, R.; Daughtry, C. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Heilman, J.L.; Heilman, W.E.; Moore, D.G. Evaluating the crop coefficient using spectral reflectance. Agron. J. 1982, 74, 967–971. [Google Scholar] [CrossRef]
- Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J., Jr. Remotely sensed crop temperatures and reflectances as inputs to irrigation scheduling. In Irrigation and Drainage: Today’s Challenges; ASCE: New York, NY, USA, 1980; pp. 390–397. [Google Scholar]
- Neale, C.M.U.; Bausch, W.C.; Heerman, D.F. Development of reflectance-based crop coefficients for corn. Trans. ASAE 1989, 32, 1891–1899. [Google Scholar] [CrossRef]
- Consoli, S.; Barbagallo, S. Estimating water requirements of an irrigated mediterranean vineyard using a satellite-based approach. J. Irrig. Drain. Eng. 2012, 138, 896–904. [Google Scholar] [CrossRef]
- Duchemin, B.; Hadria, R.; Erraki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, a.; Escadafal, R.; Ezzahar, J.; Hoedjes, J.C.B.; Kharrou, M.H.; et al. Monitoring wheat phenology and irrigation in central morocco: On the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining fao-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; Escuin, S.; Cano, F.; Cifuentes, V.; Padilla, F.L.M.; Tirado, J.L.; Oyonarte, N.; Fernández, P.; Mateos, L. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. II. Application on basin scale. Agric. Water Manag. 2013, 125, 92–104. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; Mateos, L. Spectral vegetation indices for benchmarking water productivity of irrigated cotton and sugarbeet crops. Agric. Water Manag. 2008, 95, 48–58. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Barnes, E.M.; Kimball, B.A. Estimating cotton evapotranspiration crop coefficients with a multispectral vegetation index. Irrig. Sci. 2003, 22, 95–104. [Google Scholar] [CrossRef]
- Jayanthi, H.; Neale, C.M.U.; Wright, J.L. Development and validation of canopy reflectance-based crop coefficient for potato. Agric. Water Manag. 2007, 88, 235–246. [Google Scholar] [CrossRef]
- Mateos, L.; González-Dugo, M.P.; Testi, L.; Villalobos, F.J. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. I. Method validation. Agric. Water Manag. 2013, 125, 81–91. [Google Scholar] [CrossRef]
- Chen, J.M.; Chen, X.; Ju, W.; Geng, X. Distributed hydrological model for mapping evapotranspiration using remote sensing inputs. J. Hydrol. 2005, 305, 15–39. [Google Scholar] [CrossRef]
- Cammalleri, C.; Ciraolo, G.; Minacapilli, M.; Rallo, G. Evapotranspiration from an olive orchard using remote sensing-based dual crop coefficient approach. Water Resour. Manag. 2013, 27, 4877–4895. [Google Scholar] [CrossRef]
- Er-Raki, S.; Rodriguez, J.C.; Garatuza-Payan, J.; Watts, C.J.; Chehbouni, A. Determination of crop evapotranspiration of table grapes in a semi-arid region of northwest Mexico using multi-spectral vegetation index. Agric. Water Manag. 2013, 122, 12–19. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L.; Chen, K.S.; Zhu, Y.; Liu, W. Verification of land surface evapotranspiration estimation from remote sensing spatial contextual information. Hydrol. Processes 2012, 26, 2283–2293. [Google Scholar] [CrossRef]
- CIREN. Descripciones de Suelos, Materiales y Simbolos. Estudio agrológico vii Region; Ministerio de Agricultura: Santiago, Chile, 1997; p. 659.
- United States Soil Survey Staff. Soil Taxonomy. A basic System of Soil Classification for Making and Interpreting Soil Surveys; U.S. Department of Agriculture: Washington, DC, USA, 1999; p. 886.
- Lauri, P.E.; Lespinasse, J.M. The Vertical Axis and Solaxe Systems in France; International Society for Horticultural Science (ISHS): Leuven, Belgium, 1998; pp. 287–296. [Google Scholar]
- Campos, I.; Neale, C.M.U.; López, M.-L.; Balbontín, C.; Calera, A. Analyzing the effect of shadow on the relationship between ground cover and vegetation indices by using spectral mixture and radiative transfer models. J. Appl. Remote Sens. 2014, 8, 1–21. [Google Scholar] [CrossRef]
- Muztiger, A.J.; Burt, C.M.; Howes, D.J.; Allen, R.G. Comparison of measured and fao 56 modeled evaporation from bare soil. J. Irrig. Drain.Eng. 2005, 131, 59–72. [Google Scholar]
- Torres, E.A.; Calera, A. Bare soil evaporation under high evaporation demand: A proposed modification to the fao-56 model. Hydrol. Sci. J. 2010, 55, 303–315. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J.; Romberger, J.S.; Papendick, R.I. Estimating generalized soil-water characteristics from texture. Soil Sci. Soc. Am. J. 1986, 50, 1031–1036. [Google Scholar] [CrossRef]
- Laubach, J.; Raschendorfer, M.; Kreilein, H.; Gravenhorst, G. Determination of heat and water vapour fluxes above a spruce forest by eddy correlation. Agric. For. Meteorol. 1994, 71, 373–401. [Google Scholar] [CrossRef]
- Gash, J.H.C. Observations of turbulence downwind of a forest-heath interface. Bound.-Layer Meteorol. 1986, 36, 227–237. [Google Scholar] [CrossRef]
- Li, S.; Kang, S.; Li, F.; Zhang, L.; Zhang, B. Vineyard evaporative fraction based on eddy covariance in an arid desert region of northwest China. Agric. Water Manag. 2008, 95, 937–948. [Google Scholar] [CrossRef]
- Poblete-Echeverría, C.; Ortega-Farias, S. Estimation of actual evapotranspiration for a drip-irrigated merlot vineyard using a three-source model. Irrig. Sci. 2009, 28, 65–78. [Google Scholar] [CrossRef]
- Baldocchi, D.; Rao, K.S. Intra-field variability of scalar flux densities across a transition between a desert and an irrigated potato field. Bound.-Layer Meteorol. 1995, 76, 109–136. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water-vapor transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Hui, D.; Wan, S.; Su, B.; Katul, G.; Monson, R.; Luo, Y. Gap-filling missing data in eddy covariance measurements using multiple imputation (MI) for annual estimations. Agric. For. Meteorol. 2004, 121, 93–111. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H.; et al. Gap filling strategies for long term energy flux data sets. Agric. For. Meteorol. 2001, 107, 71–77. [Google Scholar] [CrossRef]
- Payero, J.O.; Neale, C.M.U.; Wright, J.L. Estimating soil heat flux for alfalfa and clipped tall fescue grass. Appl. Eng. Agric. 2005, 21, 401–409. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Martínez-Cob, A.; Faci, J.M. Evapotranspiration of an hedge-pruned olive orchard in a semiarid area of ne Spain. Agric. Water Manag. 2010, 97, 410–418. [Google Scholar] [CrossRef] [Green Version]
- Adler-Golden, S.M.; Matthew, M.W.; Bernstein, L.S.; Levine, R.Y.; Berk, A.; Richtsmeier, S.C.; Acharya, P.K.; Anderson, G.P.; Felde, G.; Gardner, J.; et al. Atmospheric correction for short-wave spectral imagery based on MODTRAN4. SPIE Proc. Imaging Spectrom. 1999, 3753, 61–69. [Google Scholar]
- Berk, A.; Bernstein, L.S.; Robertson, D.C. Modtran: A Moderate Resolution Model for Lowtran 7; GL-TR-89-0122; Air Force Geophysics Laboratory: Bedford, MA, USA, 1989. [Google Scholar]
- Vermote, E.F.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcrette, J.J. Second simulation of the satellite signal in the solar spectrum, 6s: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat mss, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Willmott, C. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Sun, X. Temporal upscaling of instantaneous evapotranspiration: An intercomparison of four methods using eddy covariance measurements and MODIS data. Remote Sens. Environ. 2013, 138, 102–118. [Google Scholar] [CrossRef]
- Marsal, J.; Lopez, G.; Mata, M.; Arbones, A.; Girona, J. Recommendations for water conservation in peach orchards in mediterranean climate zones using combined regulated deficit irrigation. Acta Hortic. 2004, 664, 391–397. [Google Scholar] [CrossRef]
- O'Connell, M.G.; Goodwin, I. Responses of “pink lady” apple to deficit irrigation and partial rootzone drying: Physiology, growth, yield, and fruit quality. Aust. J. Agric. Res. 2007, 58, 1068–1076. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Boulet, G.; Williams, D.G. Using the dual approach of FAO-56 for partitioning et into soil and plant components for olive orchards in a semi-arid region. Agric. Water Manag. 2010, 97, 1769–1778. [Google Scholar] [CrossRef] [Green Version]
- Ortega-Farias, S.; Carrasco, M.; Olioso, A.; Acevedo, C.; Poblete, C. Latent heat flux over cabernet sauvignon vineyard using the shuttleworth and wallace model. Irrig. Sci. 2007, 25, 161–170. [Google Scholar] [CrossRef]
- Stoy, P.C.; Mauder, M.; Foken, T.; Marcolla, B.; Boegh, E.; Ibrom, A.; Arain, M.A.; Arneth, A.; Aurela, M.; Bernhofer, C.; et al. A data-driven analysis of energy balance closure across fluxnet research sites: The role of landscape scale heterogeneity. Agric. For. Meteorol. 2013, 171–172, 137–152. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Jia, Y.; Li, C.; Chen, K.-S.; Sun, X.; Lou, J. Evaluating one- and two-source energy balance models in estimating surface evapotranspiration from landsat-derived surface temperature and field measurements. Int. J. Remote Sens. 2013, 34, 3299–3313. [Google Scholar] [CrossRef]
- Katul, G.; Hsieh, C.-I.; Bowling, D.; Clark, K.; Shurpali, N.; Turnipseed, A.; Albertson, J.; Tu, K.; Hollinger, D.; Evans, B. Spatial variability of turbulent fluxes in the roughness sublayer of an even-aged pine forest. Bound.-Layer Meteorol. 1999, 93, 1–28. [Google Scholar] [CrossRef]
- Consoli, S.; Vanella, D. Comparisons of satellite-based models for estimating evapotranspiration fluxes. J. Hydrol. 2014, 513, 475–489. [Google Scholar] [CrossRef]
- Girona, J.; Campo, J.; Mata, M.; Lopez, G.; Marsal, J. A comparative study of apple and pear tree water consumption measured with two weighing lysimeters. Irrig. Sci. 2011, 29, 55–63. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Kimball, B.A. Wheat basal crop coefficients determined by normalized difference vegetation index. Irrig. Sci. 2005, 24, 1–14. [Google Scholar] [CrossRef]
- López-Urrea, R.; Montoro, A.; González-Piqueras, J.; López-Fuster, P.; Fereres, E. Water use of spring wheat to raise water productivity. Agric. Water Manag. 2009, 96, 1305–1310. [Google Scholar] [CrossRef]
- Campos, I.; Balbontín, C.; González-Piqueras, J.; González-Dugo, M.P.; Neale, C.M.; Calera, A. Combining a water balance model with evapotranspiration measurements to estimate total available soil water in irrigated and rainfed vineyards. Agric. Water Manag. 2016, 165, 141–152. [Google Scholar] [CrossRef]
- Poblete-Echeverría, C.; Ortega-Farias, S. Evaluation of single and dual crop coefficients over a drip-rrigated merlot vineyard (Vitis vinifera L.) using combined measurements of sap flow sensors and an eddy covariance system. Aust. J. Grape Wine Res. 2013, 19, 249–260. [Google Scholar] [CrossRef]
- Keller, J.; Bliesner, R.D. Sprinkle and Trickle Irrigation; Van Nostrand Reinhold: Princeton, NJ, USA, 1990. [Google Scholar]
- Green, S.; Clothier, B. The root zone dynamics of water uptake by a mature apple tree. Plant Soil 1999, 206, 61–77. [Google Scholar] [CrossRef]
- Green, S.R.; Clothier, B.E. Root water uptake by kiwifruit vines following partial wetting of the root zone. Plant Soil 1995, 173, 317–328. [Google Scholar] [CrossRef]
- Moreno, F.; Fernandez, J.E.; Clothier, B.E.; Green, S.R. Transpiration and root water uptake by olive trees. Plant Soil 1996, 184, 85–96. [Google Scholar] [CrossRef]
- Palomo, M.J.; Moreno, F.; Fernández, J.E.; Díaz-Espejo, A.; Girón, I.F. Determining water consumption in olive orchards using the water balance approach. Agric. Water Manag. 2002, 55, 15–35. [Google Scholar] [CrossRef]







| Parameter | Description | Value |
|---|---|---|
| REW (mm) | Readily evaporable water | 4 |
| TEW (mm) | Total evaporable water | 12.75 |
| Ze (m) | Depth of surface soil evaporation layer | 0.10 |
| fw | Fraction of the surface wetted | 0.3 |
| θfc (cm3·cm−3) | Field capacity | 0.38 |
| θwp (cm3·cm−3) | Wilting point | 0.25 |
| Zr max (m) | Maximum effective root deep | 0.80 |
| p | Soil depletion fraction without stress | 0.50 |
| Season 2010–2011 | Season 2012–2013 | ||
|---|---|---|---|
| Date | Sensor | Date | Sensor |
| 6 November 2010 | L7-ETM+ | 26 October 2012 | L7-ETM+ |
| 14 November 2010 | L5-TM | 11 November 2012 | L7-ETM+ |
| 30 November 2010 | L5-TM | 27 November 2012 | L7-ETM+ |
| 08 December 2010 | L7-ETM+ | 29 December 2012 | L7-ETM+ |
| 16 December 2010 | L5-TM | 30 January 2013 | L7-ETM+ |
| 1 January 2011 | L5-TM | 15 February 2013 | L7-ETM+ |
| 9 January 2011 | L7-ETM+ | 3 March 2013 | L7-ETM+ |
| 25 January 2011 | L7-ETM+ | 19 March 2013 | L7-ETM+ |
| 2 February 2011 | L5-TM | 12 April 2013 | L8-OLI |
| 26 February 2011 | L7-ETM+ | 6 May 2013 | L7-ETM+ |
| 22 March 2011 | L5-TM | 14 May 2013 | L8-OLI |
| 30 March 2011 | L7-ETM+ | ||
| 23 April 2011 | L5-TM | ||
| 1 May 2011 | L7-ETM+ | ||
| Growing Season | Daily Values | ||||||
|---|---|---|---|---|---|---|---|
| RMSE (mm·day−1) | MBE (mm·day−1) | MAE (mm·day−1) | d | Observed Average (mm) | Relative RMSE | Relative MAE | |
| 2010–2011 | 0.78 | 0.13 | 0.62 | 0.73 | 3.24 | 0.24 | 0.19 |
| 2012–2013 | 0.74 | −0.24 | 0.59 | 0.90 | 3.01 | 0.25 | 0.20 |
| Growing Season | Weekly Values | ||||||
|---|---|---|---|---|---|---|---|
| RMSE (mm·day−1) | MBE (mm·day−1) | MAE (mm·day−1) | d | Observed Average (mm) | Relative RMSE | Relative MAE | |
| 2010–2011 | 0.32 | 0.10 | 0.25 | 0.88 | 3.24 | 0.10 | 0.08 |
| 2012–2013 | 0.60 | −0.26 | 0.47 | 0.92 | 3.01 | 0.20 | 0.16 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Odi-Lara, M.; Campos, I.; Neale, C.M.U.; Ortega-Farías, S.; Poblete-Echeverría, C.; Balbontín, C.; Calera, A. Estimating Evapotranspiration of an Apple Orchard Using a Remote Sensing-Based Soil Water Balance. Remote Sens. 2016, 8, 253. https://doi.org/10.3390/rs8030253
Odi-Lara M, Campos I, Neale CMU, Ortega-Farías S, Poblete-Echeverría C, Balbontín C, Calera A. Estimating Evapotranspiration of an Apple Orchard Using a Remote Sensing-Based Soil Water Balance. Remote Sensing. 2016; 8(3):253. https://doi.org/10.3390/rs8030253
Chicago/Turabian StyleOdi-Lara, Magali, Isidro Campos, Christopher M. U. Neale, Samuel Ortega-Farías, Carlos Poblete-Echeverría, Claudio Balbontín, and Alfonso Calera. 2016. "Estimating Evapotranspiration of an Apple Orchard Using a Remote Sensing-Based Soil Water Balance" Remote Sensing 8, no. 3: 253. https://doi.org/10.3390/rs8030253
APA StyleOdi-Lara, M., Campos, I., Neale, C. M. U., Ortega-Farías, S., Poblete-Echeverría, C., Balbontín, C., & Calera, A. (2016). Estimating Evapotranspiration of an Apple Orchard Using a Remote Sensing-Based Soil Water Balance. Remote Sensing, 8(3), 253. https://doi.org/10.3390/rs8030253