Learning a Transferable Change Rule from a Recurrent Neural Network for Land Cover Change Detection

Abstract

When exploited in remote sensing analysis, a reliable change rule with transfer ability can detect changes accurately and be applied widely. However, in practice, the complexity of land cover changes makes it difficult to use only one change rule or change feature learned from a given multi-temporal dataset to detect any other new target images without applying other learning processes. In this study, we consider the design of an efficient change rule having transferability to detect both binary and multi-class changes. The proposed method relies on an improved Long Short-Term Memory (LSTM) model to acquire and record the change information of long-term sequence remote sensing data. In particular, a core memory cell is utilized to learn the change rule from the information concerning binary changes or multi-class changes. Three gates are utilized to control the input, output and update of the LSTM model for optimization. In addition, the learned rule can be applied to detect changes and transfer the change rule from one learned image to another new target multi-temporal image. In this study, binary experiments, transfer experiments and multi-class change experiments are exploited to demonstrate the superiority of our method. Three contributions of this work can be summarized as follows: (1) the proposed method can learn an effective change rule to provide reliable change information for multi-temporal images; (2) the learned change rule has good transferability for detecting changes in new target images without any extra learning process, and the new target images should have a multi-spectral distribution similar to that of the training images; and (3) to the authors’ best knowledge, this is the first time that deep learning in recurrent neural networks is exploited for change detection. In addition, under the framework of the proposed method, changes can be detected under both binary detection and multi-class change detection.

1. Introduction

With the development of remote sensing, the dynamic observation of the Earth has led to a great deal of available, detailed, accurate and up-to-date change information for use in learning about and monitoring our planet [1]. Change detection is important for detecting dynamic changes of the Earth. Change detection attempts to identify land cover differences in the same geographical area across a period of time [2] and can be applied to various domains, including urban expansion [3], disaster monitoring [4], land cover map updating [5], forest degradation survey [6] and glacier melting [7]. In this context, various types of multi-temporal images are exploited to resolve the above problems. Among them, multi-spectral data with sufficient spectra and fine spatial resolution provide a powerful ability to detect changes.

In the literature, many algorithms have been designed for detecting changes, each with different advantages. Generally, these methods can be divided into four categories as follows:

(1)

Image algebra: To detect changes directly, image differencing and image ratios are widely used to detect changes between multi-temporal images. Among them, image differencing (subtraction rule) is a robust and efficient method for detecting changes, and Change Vector Analysis (CVA) [8] represents its conceptual extension with an integrated theoretical framework, therein providing good performance.

(2)

Post-classification: Changed objects are acquired from independent classified multi-temporal maps, and land cover changes can be easily identified from the separately-classified maps. Therefore, numerous classification methods [9,10] have been proposed to improve change detection accuracy. In particular, a novel change-detection-driven transfer learning approach [11] was proposed to update land cover maps via the classification of image time series.

(3)

Feature learning and transformation: In this category, new learned (transformed) or selected features are utilized to distinguish changes, especially using a distance metric. Among the change feature learning methods, physically-meaningful features and learned change features both lead to a good performance and have been applied in various domains. As physically-meaningful features, vegetation indices, forest canopy variables and water indices are often extracted to identify changes in specific ground-object types [12,13]. For learned features and transformations, various features or transformed feature spaces are learned to highlight the change information to detect a changed region more easily than when using the original spectral information of multi-temporal images, such as in Principal Component Analysis (PCA) [14], Multivariate Alteration Detection (MAD) [15], subspace learning [16,17], sparse learning [18] and slow features [19].

(4)

Other advanced methods: Change detection can be formulated as a statistical hypothesis test using physical models [20]. The metric learning method [21] is also an effective method of detecting changes using well-learned distances. In addition, canonical correlation analysis [22,23] and clustering methods [24,25] have been proposed and found to perform well in unsupervised change detection tasks.

The above change detection methods all achieve good performances and make various contributions. However, limitations also exist and should be resolved to better detect changes. For multi-spectral images, all available spectral bands should be considered effectively to detect changes. Moreover, the learned change information should be recorded and exploited for sequential time series data with transferability. In addition, an integrated and independent change detection method can be exploited to detect changes more widely and conveniently without the supplementary task of threshold selection or classification at the final decision step.

To overcome the above limitations, we expect to design an integrated and independent change rule in our method to detect changes with all available spectral information, and the change rule can be transferred to new target multi-temporal images. Briefly, the effective change rule should have a reliable capability for change information representation, and the learned change rule can be transferred to new target images without any extra learning process, which demonstrates its transferability. In addition, in this paper, transferability is restricted to new target multi-temporal images whose spectral distributions are similar (the same number of spectral bands) to those of training multi-temporal images. Recently, some researchers [11] have proposed a change-detection-driven transfer leaning approach for updating land cover maps using classification, which has emphasized the importance of transferability in change detection research. Therefore, it is important to design an integrated change rule for detecting changes directly with transfer capacity, where the transfer capacity relies on a reliable capability in terms of the expression of the change information extraction for sequential time series data. A Recurrent Neural Network (RNN) can be used to achieve the above objectives. RNNs [26] are network models that use recurrent connections between their neural activations at consecutive time steps; such models use hidden layers or memory cells to learn the time-evolving states that model the underlying dynamics of the input sequence for sequential time series data. RNN models have gained significant attention for solving many challenging problems involving sequential time series data, especially Long Short-Term Memory (LSTM) models [27]. In an RNN learning framework, learning an appropriate representation of the sequences is an important step for achieving artificial intelligence. For change detection, it is important to have a reliable capability in terms of the expression of change information extraction for detecting changes. Thus, RNN models represent potential approaches for learning reliable difference information and providing memorability for change detection in sequential time series remote sensing data.

In this paper, we propose a new change detection method named REFEREE (learning a transferable change Rule From a recurrent neural network for change detection). The main idea of the proposed approach is learning an efficient change rule with a reliable capability in terms of the expression of difference information extraction for detecting changes. For the process of learning a reliable change rule, REFEREE provides transferability with a memory function to detect changes in an integrated change detection system. Therefore, REFEREE adapts LSTM models to resolve not only bitemporal change problems, but also multi-class change detection problems (the definition can be found in Section 2). In addition, REFEREE is the first method that exploits the RNN framework to learn a “change rule” for the change detection task on remote sensing images; moreover, a specially-designed LSTM model is tailored to represent the change information, which is not considered in traditional RNN models, such as those in the literature [28,29].

The remainder of this paper is organized as follows. The experimental data and some definitions concerning multi-class changes in this study are described in Section 2. The details of our method are presented in Section 3. The experimental setup for the parameters and the experimental design are described in Section 4. The experimental results and discussion are presented in Section 5. Section 6 concludes this paper.

2. Image Preparation

The performance of the proposed method is evaluated on three datasets. Among them, two multi-spectral datasets were acquired by the Landsat 7 Enhanced Thematic Mapper Plus (ETM+) sensor with six bands and a spatial resolution of 30 m. The last dataset was selected from images obtained by the EO-1 Hyperion, which is the first civil hyperspectral sensor on-board the Earth Observing One (EO-1) satellite and includes 242 spectral bands with a spatial resolution of 30 m. With the restricted condition of the spectral distributions in the transfer experiments (more details can be found in Section 4.3), only six bands, which are similar to the band range of the ETM sensor, were selected from the EO-1 Hyperion images for evaluating the REFEREE model. Before using these data, the digital numbers (DNs) of the original data can be converted into absolute radiance (i.e., all of the datasets utilized in the experiments are normalized into a range of [0, 1]). Moreover, both the experimental datasets and corresponding ground truth are acquired from the literature [19].

(1) Taizhou images: The first dataset consists of two images acquired for the city of Taizhou, China, in March 2000 ($T_1$) and February 2003 ($T_2$), with a WGS-84 projection and a coordinate range of 31${}^{\circ }$14’55.84 N–31${}^{\circ }$27’39.26 N, 120${}^{\circ }$02’24.38 E–121${}^{\circ }$07’45.15 N. The two images are both $400\times 400$ pixels, and the two images show changes mainly related to city expansion, as shown in Figure 1a,b, in Bands 4, 3 and 2. Figure 1c,d shows the labeled binary ground truth and multi-class ground truth, respectively. Here, the multi-class changes contain unchanged regions and three classes of changed regions: city expansion (bare soil, grassland or cultivated field to buildings or roads); changed soil (cultivated field to bare soil); and changed water areas (no-water regions to water regions). Additionally, the multi-class changes are changes such that the change types can be certain, although the classes at different time steps are not certain. Taking city expansion as an example, the class characterizing one pixel may be bare soil, grassland or cultivated field at time $T_1$, whereas the class of the same geographical pixel may be a building or road at time $T_2$. Then, we are unsure if the pixel changed from a certain class to another label, whereas the change type of this pixel is certain to be city expansion. This is unsuitable for traditional supervised classification-based change detection methods that learn change information without land cover maps at different time steps.

(2) Kunshan images: The second dataset includes two images acquired for the city of Kunshan, China, in March 2000 ($t_1$) and February 2003 ($t_2$), with a WGS-84 projection and coordinate range of 32${}^{\circ }$26’09.37 N–32${}^{\circ }$32’27.61 N, 119${}^{\circ }$50’31.67 E–119${}^{\circ }$58’24.19 E. The two images are both $800\times 800$ pixels. The pseudocolor Kunshan images are presented in Figure 2a,b. Figure 2c,d shows the labeled binary ground truth and multi-class ground truth, respectively. The Kunshan images are more challenging than the Taizhou data, because they are more complex in terms of not only city expansion, but also farmland changes; additional details about multi-class definitions can be found in the above Taizhou images.

(3) Yancheng images: The third dataset includes two images acquired for the city of Yancheng, China, in May 2006 ($t_1$) and April 2007 ($t_2$), with a WGS-84 projection and approximate coordinates of 33${}^{\circ }$39’51.85 N, 120${}^{\circ }$18’16.25 E. The two images, which are $450\times 140$ pixels, consist of only six spectral bands (Bands 9, 15, 32, 55, 143 and 218 from the original EO-1 Hyperion images), and the selected bands have spectral ranges similar to those of the ETM images. Figure 3a–c shows the Yancheng images at two different time steps and the labeled binary ground truth, and the main change type is farmland changes.

3. Method

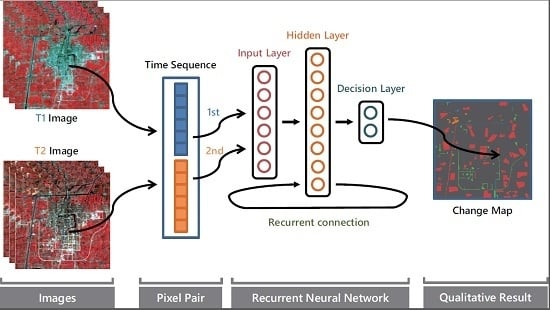
3.1. Our Proposed REFEREE Model

Figure 4 illustrates the main procedure of the REFEREE model. The input of the model includes two pixel vectors from two different time steps, and the output is a label representing changes or no changes. Applying REFEREE to all pixels over the whole images, a change map can be obtained. To be specific, the flowchart of REFEREE can be summarized as follows: First, an original pixel vector (6 spectral bands) of the $T_1$ image is fed into the input layer. Then, the hidden layer (consisting of LSTM units) receives the input and calculates the state information for the current input; it also restores those state values in the meantime. Next, the corresponding pixel vector of the $T_2$ image is input to the hidden layer with the state information of $T_1$ simultaneously, and the change information between two pixel vectors can be learned by the current hidden layer. Finally, the REFEREE model can predict the label of the changes or non-changes through the last decision layer based on the learned change information in the hidden layer. Moreover, every orange circle of the hidden layer in Figure 4 denotes an improved LSTM unit, and additional details about REFEREE are described below.

Let us consider a pair of multi-spectral images, ${\mathbf{X}}^{T_1}$ and ${\mathbf{X}}^{T_2}$, acquired over the same geographical area at two different times $T_1$ and $T_2$. Let $\mathbf{Y}=\{(0,1),(1,0)\}$, where $\mathbf{Y}$ is a set of class labels for binary change detection, in which $\mathbf{y}=(0,1)$ denotes the status of the unchanged pixels and $\mathbf{y}=(1,0)$ denotes the changed pixels. For multi-class change tasks, we use one-hot coding [30] to represent the labels Y of different change types.

In the recent literature on the RNN framework [31], recent advances in statistical machine learning and deep learning [32] have yielded state-of-the-art results with powerful sequence models. In these models, an input sequence in an “end-to-end” fashion is given for both training and inference, and the models can maximize the probability of correctly-predicted results directly. Inspired by RNN models in machine learning, we use a recurrent neural network to encode the multi-temporal image input as a fixed-dimensional vector, and the fixed input can be decoded as the output value in the training process. During the training step, the change rule of REFEREE can be learned in context layers with transferability.

Thus, the probability of obtaining the correct predicted results can be maximized directly for multi-temporal images ${\mathbf{X}}^{T_1}$ and ${\mathbf{X}}^{T_2}$ using the following formulation:

$${\theta }^{*}=arg\underset{\theta }{max}\sum _{i}p({\mathbf{y}}_i|{\mathbf{x}}_i^{T_1},{\mathbf{x}}_i^{T_2};\theta )$$

(1)

where θ is the parameter set of our model, ${\mathbf{x}}_i^{T_1}$ and ${\mathbf{x}}_i^{T_2}$ denote a pair of pixel vectors of the multi-spectral images ${\mathbf{X}}^{T_1}$ and ${\mathbf{X}}^{T_2}$ and $y_i$ is the predicted label.

We input ${\mathbf{x}}_i^{T_1}$ and ${\mathbf{x}}_i^{T_2}$ into the model as time sequence data; thus, it is natural to model $p({\mathbf{y}}_i|{\mathbf{x}}_i^{T_1},{\mathbf{x}}_i^{T_2})$ with a recurrent neural network, where the change rule is expressed by a fixed-length hidden state or memory ${\mathbf{h}}^t$. The memory is updated with a new pixel vector input using a non-linear function f, which can be described as:

$${\mathbf{h}}^{t+1}=f({\mathbf{h}}^t,x^t)$$

(2)

The important advantage of a recurrent neural network is its ability to sense contextual information when mapping the input sequence and output.

3.2. LSTM Hidden Unit and Forward Pass of the REFEREE Model

The choice of f is critical for vanishing and exploding gradient [33] issues, which are a common challenge in designing and training a recurrent neural network. The LSTM model [27] is beneficial for preventing the above problems and performs well when applied to many challenging problems involving sequential time series data. Thus, in this paper, a special LSTM model is improved for the recurrent hidden unit to address change detection for multi-temporal remote sensing data.

According to the characteristics of the change detection task, a detailed architecture of the LSTM unit is designed, as shown in Figure 5. Here, REFEREE learns the reliable difference information in a core memory cell using multi-temporal images, and the core memory cell is jointly modulated by three gates: input, output and forget gates. These gates determine the amount of dynamic information entering, leaving and updating the memory cell. In particular, the forget gate can update the internal difference information of the core memory cell. The output, which exits from the core memory cell, shows a reliable capability in terms of the expression of difference information extraction. Moreover, the core memory cell can recode and highlight the value of the binary changed samples or multi-class changes in the update process to detect changes with transferability. Additional details about the three gates are given below.

The core of the LSTM unit is a memory cell c, which encodes the difference information about the change rule. The behavior of the cell is controlled by three gates: input, output and forget gates. The gates are layers that can either decide to keep the current cell state value if the gate is 1 or to clean the memory from the gated layer if the gate is 0. Three gates are generally used to control the input, output and update of the current cell state value in the memory cell. The output of the memory cell contains the change information. The definition of the three gates, memory cell and final output are described below.

Input node: This unit, which is labeled ${\mathbf{g}}^t$, is a node that responds to activation from the input layer at the current time step $T_2$ and from the hidden layer at the previous time step $T_1$. The node merges the information at two different times and inputs this information into the cell. This unit can be formulated as follows:

$${\mathbf{g}}^{(T_2)}=\varphi ({\mathbf{W}}_{gx}{\mathbf{x}}^{T_2}+{\mathbf{W}}_{gh}{\mathbf{h}}^{T_1}+{\mathbf{b}}_g)$$

(3)

where ${\mathbf{W}}_{gx}$ and ${\mathbf{W}}_{gh}$ are coefficient matrices and ${\mathbf{b}}_g$ is the bias vector of the input node. ϕ is the activation function of the input node, the tanh function.

Gates are an important concept in LSTM. A gate is a sigmoidal unit that responds to activation from the pixel vector of $T_2$ images, as well as from the hidden layer at the $T_1$ time step. All gates in REFEREE are used to multiply the input to decide whether to pass or cut off the input value. In brief, if the value of any gate is “one” (the gate is fully open), then all of the flow is passed through. In contrast, if the value of the gate is “zero” (the gate is fully closed), the flow of the other input is cut off.

Input gate: The input gate is checked to decide whether an input should be read to the memory cell. The value of the input gate multiplies the current time pixel vector and the output of the hidden layer at the previous time step $T_1$. The pixel vectors usually contain abundant information; however, only parts of this information are beneficial for distinguishing changes or change types. Therefore, the input gate can automatically select useful information and input it into memory cell c to learn the change rule. The forward pass of the input gate is:

$${\mathbf{i}}^{(T_2)}=\sigma ({\mathbf{W}}_{ix}{\mathbf{x}}^{T_2}+{\mathbf{W}}_{ih}{\mathbf{h}}^{T_1}+{\mathbf{b}}_i)$$

(4)

where ${\mathbf{W}}_{ix}$ and ${\mathbf{W}}_{ih}$ are the coefficient matrices of the input gate and ${\mathbf{b}}_i$ is the bias vector. The activation function σ is a sigmoid function for the input gate.

Memory cell: The memory cell c facilitates information storage, in which information can be stored in, written to and read from cell c. The cell makes decisions about what data to store and when to allow reading, writing and erasure via open or closed gates. During the training process, the memory cell c learns to obtain the best state that can highlight the pair of pixel vector changed samples. At the heart of the memory cell c is the internal state node $s_c$ with linear activation, and the internal state $s_c$ has a self-connected recurrent edge with a fixed unit weight. Moreover, the internal state $s_c$ can learn and record important information across time steps because the edge of $s_c$ spans adjacent time steps $T_1$ and $T_2$ with constant weight. In vector notation, the update for the cell state can be defined as follows:

$${\mathbf{s}}^{T_2}={\mathbf{g}}^{T_2}\odot {\mathbf{i}}^{T_2}+{\mathbf{s}}^{T_1}$$

(5)

where ⊙ denotes point-wise multiplication and ${\mathbf{s}}^{T_1}$ is the previous state of the memory cell.

Forget gate: Although the memory cell can detect and store the difference information of multi-temporal images, the stored information in memory cell c is redundant, and this part of the redundant information may prevent the memory cell from learning the change rule effectively to some extent. Therefore, we need to set a forget gate that can decide what information we need to throw away from the cell’s internal state when a recurrent neural network is learning the change rule for optimization. The inputs of the forget gate are the pixel vector of the $T_2$ image and the calculated state information of the hidden layer at the $T_1$ time step. The output of the forget gate is a vector that can gradually control what part of the information in the memory cell will remain from the point-wise multiplication operation. For example, if the gate is fully closed (i.e., so-called “0”), that means to completely discard the current information. If the gate is completely open (i.e., “1”), all of the current information of the memory cell will remain. The state of the forget gate is determined by the training procedure of the network. The forget gate provides a method by which the network can learn to flush the contents of the internal state $s_c$. The forward pass of the forget gate can be described as follows:

$${\mathbf{f}}^{(T_2)}=\sigma (W_{fx}{\mathbf{x}}^{T_2}+W_{fh}{\mathbf{h}}^{T_1}+{\mathbf{b}}_f)$$

(6)

where ${\mathbf{b}}_f$ is the bias vector of the forget gate. ${\mathbf{W}}_{fx}$ and ${\mathbf{W}}_{fh}$ are the coefficient matrices.

The equation used to calculate the internal state on the forward pass for the forget gates is:

$${\mathbf{s}}^{T_2}={\mathbf{g}}^{T_2}\odot {\mathbf{i}}^{T_2}+{\mathbf{f}}^{T_2}\odot {\mathbf{s}}^{T_1}$$

(7)

Output gate: The value ultimately produced by a memory cell is the value of the internal state $s_c$ multiplied by the value of the output gate. The output gate decides what the unit will output, which is a filtered version based on the cell state. To obtain a suitable output from our model, a sigmoid layer is run first to decide what parts of the cell state the unit should output. Then, applying a non-linear function to the cell state and multiplying it by the output of the sigmoid gate, we obtain the final output, parts of which are relevant to the change detection task. The forward pass of the output gate is:

$${\mathbf{o}}^{(T_2)}=\sigma ({\mathbf{W}}_{ox}{\mathbf{x}}^{T_2}+{\mathbf{W}}_{oh}{\mathbf{h}}^{T_1}+{\mathbf{b}}_o)$$

(8)

where ${\mathbf{W}}_{ox}$ and ${\mathbf{W}}_{oh}$ are the coefficient matrices of the output gate and ${\mathbf{b}}_o$ is the bias vector.

Additionally, we add some peephole connections to our proposed REFEREE model. The peephole connections can pass from the internal state directly to the input, output and forget gates. The intuition behind introducing the peephole connection can be captured by the following example. During the training process, the network can capture some activation in the internal state $s_c$ after only inputting the $T_1$ pixel in the model, and then, the activation is incremented and updated in the internal state $s_c$ when the $T_2$ pixel vector is input. In this way, the internal state $s_c$ can trap the integral activation information from the $T_1$ pixel vector and the $T_2$ pixel vector. If there are changed pixels, the network will record some difference information in the internal state, and the internal state will provide feedback to the affected output gate. In this way, the internal state $s_c$ is the input of ${\mathbf{o}}^t$, and the output gate will offer an optimized value for the final output of this model to detect changed samples more easily, which is why the peephole connection is important to the REFEREE model.

The forward pass of an LSTM unit is defined as follows:

Input node:

$${\mathbf{g}}^{(T_2)}=\varphi ({\mathbf{W}}_{gx}{\mathbf{x}}^{T_2}+{\mathbf{W}}_{gh}{\mathbf{h}}^{T_1}+{\mathbf{b}}_g)$$

(9)

Input gate:

$${\mathbf{i}}^{(T_2)}=\sigma ({\mathbf{W}}_{ix}{\mathbf{x}}^{T_2}+{\mathbf{W}}_{ih}{\mathbf{h}}^{T_1}+{\mathbf{W}}_{ic}{\mathbf{s}}^{T_1}+b_i)$$

(10)

where ${\mathbf{W}}_{ic}$ is the coefficient matrix of the peephole connection that links the input gate and cell.

Forget gate:

$${\mathbf{f}}^{(T_2)}=\sigma ({\mathbf{W}}_{fx}{\mathbf{x}}^{T_2}+{\mathbf{W}}_{fh}{\mathbf{h}}^{T_1}+{\mathbf{W}}_{fc}{\mathbf{s}}^{T_1}+b_f)$$

(11)

where ${\mathbf{W}}_{fc}$ is the peephole connection matrix of the forget gate and memory cell.

Output gate:

$${\mathbf{o}}^{(T_2)}=\sigma ({\mathbf{W}}_{ox}{\mathbf{x}}^{T_2}+{\mathbf{W}}_{oh}{\mathbf{h}}^{T_1}+{\mathbf{W}}_{oc}{\mathbf{s}}^{T_1}+b_o)$$

(12)

where ${\mathbf{W}}_{oc}$ is the peephole connection matrix of the output gate and cell c.

Cell output:

$${\mathbf{s}}^{T_2}={\mathbf{g}}^{T_2}\odot {\mathbf{i}}^{T_2}+{\mathbf{f}}^{T_2}\odot {\mathbf{s}}^{T_1}$$

(13)

LSTM output:

$${\mathbf{h}}^{T_2}=\varphi ({\mathbf{s}}^{T_2})\odot {\mathbf{o}}^{T_2}$$

(14)

To better understand the internal operation modes of a recurrent neural network, we unroll the loop, as shown in Figure 6. Its chain-like nature reveals that the recurrent network is intimately related to the sequence, and the natural architecture of a neural network is a promising way of addressing change detection tasks for multi-temporal images.

3.3. Optimization

Suppose that we have a loss l that we wish to minimize at time step $T_2$ and that the loss l depends on the output of decision layer $\widehat{\mathbf{y}}$ and the ground truth label $\mathbf{y}$ via a loss function f:

$$l=f({\widehat{\mathbf{y}}}^{T_2},\mathbf{y})$$

(15)

where f can be any differentiable loss function, such as the Euclidean loss:

$$l=f({\widehat{\mathbf{y}}}^{T_2},\mathbf{y})={\parallel {\widehat{\mathbf{y}}}^{T_2}-\mathbf{y}\parallel }^2$$

(16)

Our ultimate goal in this case is to use gradient descent to minimize the loss L over the two images ${\mathbf{X}}^{T_1}$ and ${\mathbf{X}}^{T_2}$:

$$L=\sum _{t=T_1}^{T_2}l(t)$$

(17)

We now work through the algebra to compute the loss gradient $\frac{dL}{dw}$, where w is a scalar parameter of the model. Because the loss $l=f({\widehat{\mathbf{y}}}^{T_2},\mathbf{y})$ only depends on the values of the decision layer $\widehat{\mathbf{y}}$, hidden layer $\mathbf{h}$ and ground truth label $\mathbf{y}$, we define the chain rule:

$$\frac{dL}{dw}=\sum _{t=T_1}^{T_2}\sum _{j=1}^N\sum _{i=1}^M\frac{dL}{d{\widehat{y}}_j(t)}\frac{d{\widehat{y}}_j(t)}{d{h}_i(t)}\frac{d{h}_i(t)}{dw}$$

(18)

where $h_i(t)$ is the scalar corresponding to the i-th hidden output of the memory cell, M is the total number of memory cells, ${\widehat{y}}_j(t)$ is the j-th unit of the decision layer and N is the number of decision layer units. Because the network propagates information forward in time, changing ${\widehat{y}}_j(t)$ and $h_i(t)$ will not affect the loss prior to time t, which allows us to write:

$$\frac{dL}{d{\widehat{y}}_j(t)}=\sum _{s=T_1}^{T_2}\frac{dl(s)}{d{\widehat{y}}_j(t)}=\sum _{s=t}^{T_2}\frac{dl(s)}{d{\widehat{y}}_j(t)}$$

(19)

For notational convenience, we introduce the variable $L(t)$, which represents the cumulative loss from time step t onward:

$$L(t)=\sum _{s=t}^{s=T_2}l(s)$$

(20)

In this case, $L(T_1)$ is the loss for both images ${\mathbf{X}}^{T_1}$ and ${\mathbf{X}}^{T_2}$, which allows us to rewrite Equation (19) as:

$$\frac{dL}{d{\widehat{y}}_j(t)}=\sum _{s=t}^{T_2}\frac{dl(s)}{d{\widehat{y}}_j(t)}=\frac{dL(t)}{d{\widehat{y}}_j(t)}$$

(21)

We can now define the gradient calculation $\frac{dL}{dw}$ as follows:

$$\frac{dL}{dw}=\sum _{t=T_1}^{T_2}\sum _{j=1}^N\sum _{i=1}^M\frac{dL(t)}{d{\widehat{y}}_j(t)}\frac{d{\widehat{y}}_j(t)}{d{h}_i(t)}\frac{d{h}_i(t)}{dw}$$

(22)

The computation of $\frac{d{h}_i(t)}{dw}$ and $\frac{d{\widehat{y}}_j(t)}{d{h}_i(t)}$ follows directly from the forward propagation equations. The key question is how to compute $\frac{dL(t)}{d{\widehat{y}}_j(t)}$. In this paper, we utilize back-propagation using the time algorithm to resolve these issues. First, we can express the following recursion based on the variable $L(t)$:

$$L(t)=\left\{\begin{array}{cc}l(t)+L(t+1)\hfill & t<T\hfill \\ l(t)\hfill & t=T\hfill \end{array}\right.$$

(23)

Hence, given the activation $\mathbf{h}$ of an LSTM node at time step t, we have that:

$$\frac{dL(t)}{d\widehat{\mathbf{y}}(t)}=\frac{dl(t)}{d\widehat{\mathbf{y}}(t)}+\frac{dL(t+1)}{d\widehat{\mathbf{y}}(t)}$$

(24)

The first term $\frac{dl(t)}{d\widehat{\mathbf{y}}(t)}$ is simply the element-wise derivative of the loss $l(t)$ with respect to the activations $\widehat{\mathbf{y}}(t)$ at time step t. The second term $\frac{dL(t+1)}{d\widehat{\mathbf{y}}(t)}$ is the recurrent nature of LSTM, which shows that we need the derivative information of the next node to compute the derivative information of the current node. Because $\frac{dL(t)}{d\widehat{\mathbf{y}}(t)}$ for both times $T_1$ and $T_2$ is to be computed, we start by computing $\frac{dL(T_2)}{d\widehat{\mathbf{y}}(T_2)}=\frac{dl(T_2)}{d\widehat{\mathbf{y}}(T_2)}$ and work backward through the network.

4. Experimental Setup and Design

This section is structured as follows: (1) describing the competitors (comparison methods); (2) tuning the parameters of the REFEREE model and competitors; and (3) arranging the whole experimental design for the study of the sensitivity of REFEREE.

4.1. Competitors

In this paper, the results obtained using the REFEREE method are compared to those from several other methods: (1) unsupervised Change Vector Analysis (CVA) [8], which is an effective method for multi-spectral change detection tasks; (2) PCA [34], which is simple in computation and can be applied to real-time applications; (3) Iteratively-Reweighted Multivariate Alteration Detection (IRMAD) [15], which is a classical transformation change detection method for multi-spectral data; (4) Supervised Slow Feature Analysis (SSFA) [19], which is one of the latest feature learning methods for change detection; (5) Support Vector Machine (SVM) [35], which is effective for remote-sensing image classification; (6) decision tree [36], which is a tree structure consisting of internal and terminal nodes that process data to ultimately yield a classification; and (7) Convolutional Neural Network (CNN) [37], which is a hierarchical architecture trained on large-scale datasets and that has shown promising performance in classification and detection. Among these methods, CVA, PCA, IRMAD and SSFA are used in binary experiments, and SVM, decision tree and CNN are compared to REFEREE in multi-class experiments. Additionally, the proposed REFEREE method and other methods are evaluated based on kappa coefficients, the Overall Accuracy (OA) value and the F-score.

4.2. Setup of Parameters

The REFEREE model is trained with the RMSpropalgorithm [38], and the suggested default parameters are used for all of the following experiments. In REFEREE, we use a single-layer LSTM of size 512 with sigmoid gate activations and tanh activation for hidden representations, where the sigmoid gate activations and tanh activation are both default settings under the RNN framework. The decision layer uses sigmoid activation and then outputs a two-dimensional vector for binary change detection tasks and three- and four-dimensional vectors for Kunshan and Taizhou multi-class change tasks. All weight matrices in our model and the bias vector are initialized from a uniform distribution, and the values of these weight matrices and the bias vector are initialized in the range [−0.1, 0.1]. Then, all of the weight matrices and bias vectors can be updated during learning processing. In addition, we use dropout with a probability of 0.5 on the output of each LSTM to avoid overfitting.

Concerning the competitors, the threshold is an important parameter in the CVA, PCA, IRMAD and SSFA methods, and k-means clustering [39] is selected for automatic threshold selection. In the binary experiments, changes and non-changes can be regarded as a two-class classification problem [19]. Therefore, the number k in k-means clustering is two. For the SVM method, LibSVM [35] is selected to evaluate the final multi-class changes, where the kernel is the radial basis function, the cost parameter is 100 and gamma is 0.01. For the decision tree method in this paper, the maximum tree count parameter is 50, the minimum number of objects per leaf is two and the confidence factor for pruning is 0.1. For the CNN method, the parameters (i.e., the weights in the convolutional and FC layers) are trained with classic stochastic gradient descent based on the back-propagation algorithm [40].

4.3. Experimental Design

To demonstrate the effectiveness of REFEREE, three experiments are designed in this paper: binary experiments, transfer experiments and multi-class change experiments.

Binary experiments: We select some training samples from multi-temporal images to test the change detection results derived from the remaining samples. The final results are represented in terms of the average accuracy acquired from ten trials, which rely on ten initial randomly-selected training samples from the $T_1$ image and the corresponding initial samples from the $T_2$ image. Wu et al. [19] had labeled some test samples according to a detailed visual analysis of multi-temporal images and some prior information, and these labeled samples are also used to quantitatively evaluate the performance of REFEREE and its competitors. For each trial, additional details about the number of training samples, testing samples and all labeled test samples are summarized in

Table 1. The number of training/testing samples for binary experiments, transfer experiments and multi-class change experiments on the Taizhou and Kunshan images (the units of un mean unchanged samples and the units of c mean changed samples). Additional details on the change types and multi-class definitions can be found in Section 2.

		Labeled Samples	Training Samples	Testing Samples
Taizhou	binary	21,116	700
	experiment	(16,890un, 4226c)	(500 un,200c)	20,416
			200 (150un,50c)
	transfer	21,116	400 (300un,1000c)	64,183
	experiment	(16,890un, 4226c)	600 (450un,150c)	(Kunshan)
	(T-K)		800 (600un,2000c)	63,000
	(T-Y)		1000 (650un,250c)	(Yancheng)
		3172 (city change)	200	2922
	multi-class	564 (soil change)	50	514
	experiment	490 (water change)	50	440
		16,890 (unchanged)	50	11890
Kunshan	binary	64,183	1000
	experiment	(48,119un, 16,064c)	(500un,500 c )	63183
			200 (100un,100c)
	transfer	64,183	400 (200un,200c)	21,116
	experiment	(48,119un, 16,064c)	600 (300un,300c)	(Taizhou)
	(K-T)		800 (400un,400c)	63,000
	(K-Y)		1000 (500un,5000c)	(Yancheng)
	multi-class	9958 (city change)	500	9458
	experiment	6506 (farmland change)	500	6006
		48,119 (unchanged)	500	43,119
Yancheng	binary	63,000	500
	experiment	(44,723un, 18,277c)	(250un,250 c)	63,000
			200 (100un,100c)
	transfer	63,000	400 (200un,200c)	21,116
	experiment	(44,723un, 18,277c)	600 (300un,300c)	(Taizhou)
	(Y-T)		800 (400un,400c)	64183
	(Y-K)		1000 (500un,5000c)	(Kunshan)

, where units of un denote unchanged samples and units of c denote changed samples.

Transfer experiments: The training samples are selected from training multi-temporal images (A), whereas the testing samples are selected from new target multi-temporal images (B, B≠A) to test whether the change rule learned from the training multi-temporal images (A) is suitable for new multi-temporal images (B, B≠A). This is defined as transferability. In this paper, training images and new target images should have similar multi-spectral distributions (the same number of spectral bands). In the transfer experiments, the REFEREE method is only trained once on the training images (A) and is applicable without further training on arbitrary new target images. Specifically, we select a set number of training samples from the Taizhou images, and testing samples are selected from all labeled Kunshan samples without any extra information and vice versa. Additionally, to simulate challenging real-life training and transfer conditions, we provide results for a wide range of training data size conditions. In many change detection situations, especially for supervised methods, the training samples may not be sufficiently fine to detect changes over the whole remote sensing data, and less training data will not result in good features for change detection. Therefore, REFEREE is experimented with over a range of training data sizes. We randomly select 200, 400, 600, 800 and 1000 training samples from training images to test the performance on whole labeled test samples of the other new images. The final results show the average accuracy acquired from ten trials performed independently. Additional details about the number of training samples and testing samples can be found in Table 1.

Multi-class change experiments: Regarding change detection as a classification task, we utilize REFEREE with the input of pixel spectral information from two different time steps, and the output is the encoded multi-class change information. Additional details about the definition of multi-class change and change types are described in Section 2. To synthetically evaluate the performance of REFEREE for multi-class change detection, the numbers of labeled samples, training samples and testing samples are summarized in Table 1. The final results show the average accuracy acquired from ten trials performed independently.

5. Results and Discussion

This section reports and discusses all of the results of the binary experiments, transfer experiments and multi-class change experiments.

5.1. Results and Discussion of the Binary Experiments

Figure 7, Figure 8 and Figure 9 show binary change maps and confidence level maps obtained by REFEREE on the Taizhou images, the Kunshan images and the Yancheng images, respectively. The binary change maps in Figure 7a,c, Figure 8a,c and Figure 9a clearly show the main changed regions in the labeled area. Moreover, REFEREE also provides the confidence level of the detected changed samples, as shown in Figure 7b,d, Figure 8b,d and Figure 9b. In the confidence level maps, the brighter the color is, the greater the probability that the sample belongs to the changed sample. In contrast, a darker color indicates a lower probability that the sample is a changed sample. For example, white in the confidence level map indicates that the probability that the sample is a changed sample is one (i.e., 100 percentage probability), whereas black indicates that the probability that the sample is a changed sample is zero. A value between zero and one indicates a different probability or confidence level that the sample is a changed sample. From the confidence level maps of the changed region, it can also be found that changed regions almost all have a highlighted value, whereas unchanged regions are very dark. The confidence values spread mostly over the two terminal values (zero and one), and the intermediate values are limited. Therefore, it can be concluded that the REFEREE method can distinguish the changed and unchanged regions directly with the reliable difference learning ability in the core memory cell.

Table 2. The kappa coefficients for the state-of-the-art methods on the two experimental datasets. CVA, Change Vector Analysis; IRMAD, Iteratively-Reweighted Multivariate Alteration Detection; SSFA, Supervised Slow Feature Analysis.

	TaiZhou		KunShan		Yancheng
	KAPPA	OA	KAPPA	OA	KAPPA	OA
CVA	0.3755	0.6982	0.4011	0.7160	0.7907	0.8722
PCA	0.5413	0.7419	0.633	0.7741	0.8174	0.9025
IRMAD	0.7942	0.9133	0.87	0.9397	0.6973	0.8352
SSFA	0.8229	0.9454	0.9361	0.9763	0.9032	0.9516
REFEREE	0.9477	0.9777	0.9573	0.9837	0.9563	0.9828

summarizes the kappa coefficients and OA values using all of the methods on the two experimental datasets of the labeled samples, and the highest accuracy is obtained by REFEREE. The classical approaches CVA, PCA, IRMAD and SSFA all achieve a good performance, especially the SSFA method, which achieves the best performance for single-band analysis [19]. However, for a real-life remote sensing analysis process, we prefer to use all of the spectral information to detect changes with high accuracy rather than attempt using each band and select the best-performing band to detect changes. This is because it is very difficult to test and select suitable bands from a very large remote sensing dataset individually. Here, REFEREE uses all available spectral bands and yields the best performance among all methods.

5.2. Results and Discussion of the Transfer Experiments

An efficient change rule should have robust transferability. In this experimental part, REFEREE is applied to the transfer experiments, and the results show that REFEREE has remarkable transferability. From Section 5.1, it can be seen that REFEREE yields a good performance on the Taizhou images (T), Kunshan images (K) and Yancheng images (Y), with a reliable change learning ability in the binary experiments. If the learned change rule used by REFEREE is stable and robust, it should yield efficient transferability for new target images. Therefore, the transfer experimental results are presented and discussed in this subsection.

Six transfer experiments, the T-K, T-Y, K-T, K-Y, Y-T and Y-K transfer experiments, are designed with cross-validation over three images in this section. Here, T denotes Taizhou images, K denotes Kunshan images and Y denotes Yancehng images. Specifically, for the K-T transfer experiments, the training samples are selected from the Kunshan images, whereas the testing samples are all of the labeled Taizhou samples. Similarly, in the T-K transfer experiments, the training samples are selected from the Taizhou images, and the testing samples are all of the labeled Kunshan samples. By that analogy, the K-Y, T-Y, Y-T and Y-K transfer experiments can be understood clearly.

Additionally, to simulate challenging real-world training conditions, we provide results for a wide range of training dataset size conditions. We report the results over a range of training numbers (N) to test the final transfer results. For example, an N value of 200 (N = 200) indicates that only 200 training samples (100 unchanged samples and 100 changed samples) are selected from the training images (Taizhou or Kunshan) to test all labeled test samples in the new target images (Kunshan or Taizhou). Similarly, an N value of 1000 (N = 1000) indicates that 1000 training samples (500 unchanged samples and 500 changed samples) are used in the transfer experiments.

Table 3. The transfer experiment results for five training samples in the T-K and K-T experiments. OE, Overall Error.

		OA	Kappa	FP	FN	OE
T-K	N = 200	0.8652	0.5870	326	8613	8939
	N = 400	0.8579	0.5574	202	9223	9425
	N = 600	0.8717	0.6122	428	8083	8511
	N = 800	0.8652	0.6028	1236	7705	8941
	N = 1000	0.8693	0.6009	270	8398	8668
T-Y	N = 200	0.9508	0.8852	286	2816	3102
	N = 400	0.9694	0.9265	651	1275	1926
	N = 600	0.9653	0.9178	356	1828	2184
	N = 800	0.9724	0.9335	629	1110	1739
	N = 1000	0.9721	0.9334	323	1437	1760
K-T	N = 200	0.9243	0.7116	15	1772	1787
	N = 400	0.9506	0.8428	279	808	1087
	N = 600	0.9536	0.7931	387	1030	1417
	N = 800	0.9481	0.8341	279	863	1141
	N = 1000	0.9508	0.8363	23	1060	1083
K-Y	N = 200	0.9592	0.9032	251	2052	2303
	N = 400	0.9701	0.9227	824	1058	1882
	N = 600	0.9675	0.9227	364	1684	2048
	N = 800	0.9712	0.9310	481	1334	1815
	N = 1000	0.9741	0.9379	383	1251	1634
Y-T	N = 200	0.7637	0.4326	1223	2982	3205
	N = 400	0.7984	0.4638	1210	1815	3025
	N = 600	0.8894	0.6559	1094	1342	2436
	N = 800	0.8942	0.7100	1230	918	2148
	N = 1000	0.8939	0.6993	1113	1223	2336
Y-K	N = 200	0.7189	0.2760	9164	9479	18,643
	N = 400	0.7689	0.3125	4240	9706	13,946
	N = 600	0.7932	0.5152	9607	4245	13,852
	N = 800	0.8336	0.4883	1301	9737	11,038
	N = 1000	0.8428	0.5571	606	8823	9429

summarizes the transfer results over five training data sizes in six transfer experiments. Moreover, five indices are used to provide a quantitative analysis of the change detection results: Overall Accuracy (OA), False Positives (FPs), False Negatives (FNs), Overall Error (OE) and Kappacoefficients [41]. Generally, the different training data sizes available yield different results. We prefer a very high performance with a small number of training samples rather than a large number of samples in deep learning. The proposed method can be used widely. Note that, from Table 3, REFEREE can yield a good performance in all transfer experiments over the five training data size ranges. For all transfer experiments, the OE value is stable and even shows some slight downward trend with increasing number of training samples, which indicates that REFEREE can also offer a good performance with small training data sizes in the transfer experiments. Moreover, compared to the FN values of the training data sizes, the FP values are much smaller, which means that REFEREE can detect almost all changed samples directly. In particular, it can be found that the K-T, K-Y and T-Y transfer experiments yield better results than the T-K, Y-K and Y-T transfer experiments; in particular, the FP values in the K-T, T-Y and K-Y experiments are higher than those in the T-K, Y-T and Y-K experiments. The reason for this is related to the complexity of land cover changes in the training steps, which means that the Kunshan images present more complex changes than do the Taizhou images and Yancheng images. In addition, REFEREE can learn a more stable change rule from the Kunshan images than from the Taizhou and Yancheng images. Additional details about the complexity of land cover changes in the Taizhou, Kunshan and Yancehng images are described in Section 2. Moreover, the K-T and K-Y experiments performed well and also demonstrate the above results. Although there exists some error in the final detected changes, all false alarm rates were low in the transfer experiments, which means that REFEREE can offer a robust change rule for detecting changes in transfer experiments via training with complex changed samples. In summary, REFEREE can achieve a good performance in all transfer experiments, and small training samples are also effective at yielding a good performance by REFEREE.

Figure 10, Figure 11 and Figure 12 present the binary change maps and confidence level maps of the K-T, T-K and T-Y transfer experiments, respectively, over a range of training samples. Moreover, binary change maps and confidence level maps of the K-Y, T-Y and T-K transfer experiments can be found in the Supplementary Material. All of the binary change maps clearly show that the main changed regions are detected from new target images, and all binary maps demonstrate that more of the changed area can be detected from the testing samples with increasing training data size. The confidence level maps also show that REFEREE can highlight almost all of the changed samples for all five training data sizes, and the unchanged samples appear darker in the confidence level maps with increasing training data sizes. This indicates that REFEREE can highlight the difference information of the changed samples and repress the unchanged information in a more stable manner with increasing training data size.

Considering the above results and discussion, the REFEREE method is a promising method for transfer learning. The core memory cell has a robust ability to record the difference information from multi-temporal images, and the recorded information can be used for other new target multi-temporal images without utilizing an extra learning process. Moreover, if the training samples contain complex changes, the performance of REFEREE increases and becomes more stable.

5.3. Results and Discussion of the Multi-Class Change Experiments

To better assess the effectiveness of the REFEREE method in more detail, a more complex situation in which multi-class changes are present in the experimental data is considered and tested in this study. Similar to the binary experiments, several samples are selected as training samples, and the remaining labeled samples are selected as testing samples with different class changes. Additional details about the multi-class change definitions and change types can be found in Section 2.

Figure 13 shows the multi-class change results of the Taizhou images and provides the confidence level maps of different class changes and unchanged types. Figure 13a–d presents the confidence level maps of the city expansion, soil change, water change and unchanged samples. The brighter the color is, the larger the probability that the sample belongs to the corresponding change types. For example, white in the confidence level map indicates that the probability that the sample belongs to the corresponding change type is one (i.e., 100 percent), whereas pure black indicates that the probability that the sample belongs to the corresponding change type is zero; unlabeled samples are also indicated in pure black. By analyzing Figure 13a–d, it can be observed that all of the changed regions (city expansion, soil change and water change) and the unchanged region are highlighted in their own confidence level maps, thus demonstrating that REFEREE is effective at detecting different change types. Moreover, the final change type result map (Figure 13e) acquired by REFEREE shows that the changed region is almost always detected, although some error is observed in terms of detecting unchanged samples. Although some false detections are observed, REFEREE can yield a high OA value of 0.9537 and a kappa coefficient of 0.8689 on the Taizhou images. Moreover, each change class also achieved a high overall accuracy, as shown in

Table 4. The overall accuracy, kappa coefficients and F-score obtained using the REFEREE method and competitors on two experimental datasets with multi-class changes, where (C) indicates a changed type; additional information about change types can be found in Section 2. CNN, Convolutional Neural Network.

		OA	Kappa	F-score
				Unchanged	City (C)	Water (C)	Soil (C)	Farmland (C)
Taizhou	REFEREE	0.95	0.8689	0.9788	0.7887	0.8749	0.7524	/
	CNN	0.9235	0.8063	0.9675	0.6679	0.8721	0.5521	/
	SVM	0.8391	0.6758	0.8717	0.5203	0.8326	0.3558	/
	Decision tree	0.7113	0.5221	0.8701	0.6403	0.7496	0.3558	/
Kunshan	REFEREE	0.9587	0.8988	0.9432	0.9735	/	/	0.8750
	CNN	0.9336	0.8413	0.8844	0.9559	/	/	0.8491
	SVM	0.8024	0.6654	0.6830	0.8762	/	/	0.3743
	Decision tree	0.6979	0.4844	0.6642	0.7913	/	/	0.1542

.

The experimental results on the Kunshan images also demonstrate that REFEREE has a stable and efficient ability to detect multi-class changes. Figure 14 shows the multi-class change results on the Kunshan images. Figure 14a–c presents the confidence level maps of the city expansion, farmland change and unchanged samples. By analyzing the above confidence level maps and overall accuracy, it can be found that both the changed samples with different change types and the unchanged samples are almost always highlighted and detected in their own confidence level map. In addition, the final change result map (Figure 14d) shows that almost all changed regions with different change types and the unchanged region are recognized.

Table 4 reports the quantitative assessment based on the overall accuracy, kappa value and F-score for the REFEREE, CNN, SVM and decision tree methods. In Table 4, unchanged indicates the unchanged region (class), and (C) indicates changed classes. Specifically, city (C) indicates the changed type of city expansion; water (C) indicates a non-water region changing to water; soil (C) indicates cultivated field or grassland (or any non-bare soil class) changing to bare soil; and farmland (C) indicates farmland changes. Additional details on the changed types can be found in Section 2. The SVM and decision tree-based change detection methods performed well in the multi-class change detection experiments in terms of the OA, kappa and F-score values. However, the CNN-based change detection method and REFEREE both achieved higher OA, kappa and F-score values. The REFEREE method produced the best quantitative assessment in terms of all three indices, which means that our learned model is an effective way of learning change information based on multi-class changes. In particular, concerning the F-score, for soil (C) and farmland (C), REFEREE achieved a $40\%$ higher F-score than did the SVM and decision tree methods. In addition, CNN also represents a promising way to learn features and perform classification using artificial neural networks, and our model can perform slightly better than the CNN method in terms of all quantitative assessment indices.

Regarding change detection as a classification task, we utilize REFEREE with pixels from two different time steps as input and the encoded change information as output. As demonstrated by the above experiments, the REFEREE method achieves a good performance in not only the binary experiments, but also the multi-class change experiments.

6. Conclusions

In this paper, a new change detection algorithm named REFEREE that can detect not only binary changes with stable transferability, but also multi-class changes has been proposed. By introducing and improving the basic RNN framework with the LSTM model, the proposed REFEREE algorithm can provide a stable change rule for detecting changes from multi-temporal remote sensing data. Compared to other state-of-the-art algorithms, the superiority of REFEREE mainly depends on learning a stable and transferable change rule by recording the difference information or multi-class changes in a core memory cell. In addition, as demonstrated by the experimental results in this paper, the superiority of REFEREE can be summarized through three main contributions as follows: (1) REFEREE can learn a stable change rule, and the core memory can record the reliable difference information; (2) compared to other state-of-the-art algorithms, REFEREE can detect not only binary changes, but also multi-class changes for multi-temporal images; (3) the REFEREE method also has good transferability for detecting changes in new target images without any extra learning process. The new target images should have multi-spectral distributions similar (the same number of spectral bands) to those of the training images in this paper.

As demonstrated in this paper, REFEREE is robust and stable when detecting both binary and multi-class changed samples. However, the method still suffers from various issues. For example, a small number of unchanged samples is mistaken as changed samples; this issue should be resolved in future work to render REFEREE more effective. We will attempt to improve the REFEREE method to be able to detect a new changed type when the relevant training samples do not exist.