Tower-Based Validation and Improvement of MODIS Gross Primary Production in an Alpine Swamp Meadow on the Tibetan Plateau
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. Ground Measurements
2.3. MODIS Data Products
2.4. EC-Based GPP Estimation
2.5. FPAR Estimation
2.6. εmax Estimation
2.7. Revised GPP Estimation
2.8. Statistical Analysis
3. Results
3.1. Ground Measurements and Parameters Estimation
3.2. Seasonal-Scale Contrast of GPP Estimations
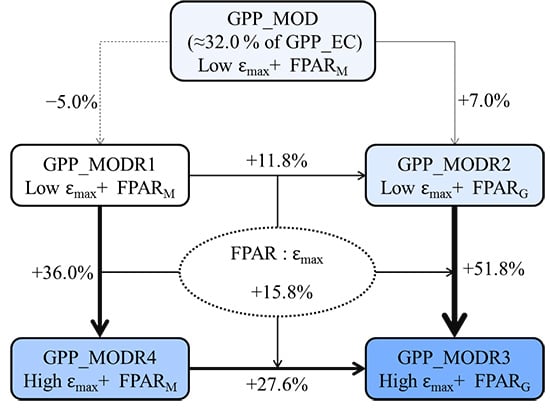
3.3. Annual-Scale Contrast of GPP Estimations
4. Discussion
4.1. Impacts of Meteorology Data on GPP Estimations
4.2. Impacts of εmax on GPP Estimations
4.3. Impacts of FPAR on GPP Estimations
4.4. Algorithm Evaluation and Uncertainty
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, G.X.; Qian, J.; Cheng, G.D.; Lai, Y.M. Soil organic carbon pool of grassland soils on the Qinghai-Tibetan Plateau and its global implication. Sci. Total Environ. 2002, 291, 207–217. [Google Scholar]
- Trumbore, S.E.; Bubier, J.L.; Harden, J.W.; Crill, P.M. Carbon cycling in boreal wetlands: A comparison of three approaches. J. Geophys. Res. Atmos. 1999, 104, 27673–27682. [Google Scholar] [CrossRef]
- Hirota, M.; Tang, Y.; Hu, Q.; Hirata, S.; Kato, T.; Mo, W.; Cao, G.; Mariko, S. Carbon dioxide dynamics and controls in a deep-water wetland on the Qinghai-Tibetan Plateau. Ecosystems 2006, 9, 673–688. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, G.; Yan, H.; Zhu, X.; Li, S.; Wang, Q.; Zhang, J.; Wang, Y.; Li, Y.; Zhao, L.; et al. A MODIS-based photosynthetic capacity model to estimate gross primary production in Northern China and the Tibetan Plateau. Remote Sens. Environ. 2014, 148, 108–118. [Google Scholar] [CrossRef]
- MÄKelÄ, A.; Pulkkinen, M.; Kolari, P.; Lagergren, F.; Berbigier, P.; Lindroth, A.; Loustau, D.; Nikinmaa, E.; Vesala, T.; Hari, P. Developing an empirical model of stand GPP with the lue approach: Analysis of eddy covariance data at five contrasting conifer sites in Europe. Glob. Chang. Biol. 2008, 14, 92–108. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global terrestrial gross and net primary productivity from the earth observing system. In Methods in Ecosystem Science; Sala, O.E., Jackson, R.B., Mooney, H.A., Howarth, R.W., Eds.; Springer New York: New York, NY, USA, 2000; pp. 44–57. [Google Scholar]
- Zhang, Y.; Wang, C.; Bai, W.; Wang, Z.; Tu, Y.; Yangjaen, D. Alpine wetlands in the Lhasa River Basin, China. J. Geogr. Sci. 2010, 20, 375–388. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Olofsson, P.; Eklundh, L.; Lagergren, F.; Jönsson, P.; Lindroth, A. Estimating net primary production for Scandinavian Forests using data from Terra/MODIS. Adv. Space Res. 2007, 39, 125–130. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Reeves, M.; Votava, P.; Kang, S.; Milesi, C.; Zhao, M.; Glassy, J.; Jolly, W.M.; Loehman, R.; Bowker, C.F. GPP and NPP (MOD17A2/A3) products NASA MODIS Land Algorithm. Available online: http://giscenter-sl.isu.edu/AOC/AOC_Satellite/MODIS/MOD17UsersGuide.pdf (accessed on 13 July 2016).
- Sánchez, M.L.; Pardo, N.; Pérez, I.A.; García, M.A. GPP and maximum light use efficiency estimates using different approaches over a rotating biodiesel crop. Agric. For. Meteorol. 2015, 214–215, 444–455. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore Iii, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Ruimy, A.; Kergoat, L.; Bondeau, A. Comparing global models of terrestrial net primary productivity (NPP): Analysis of differences in light absorption and light-use efficiency. Glob. Chang. Biol. 1999, 5, 56–64. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Baldocchi, D. Measuring biosphere-atmosphere exchange of biologically ralated gases with micrometeorological methods. Ecology 1988, 69, 1331–1340. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Hanan, N.P.; Burba, G.; Verma, S.B.; Berry, J.A.; Suyker, A.; Walter-Shea, E.A. Inversion of net ecosystem CO2 flux measurements for estimation of canopy par absorption. Glob. Chang. Biol. 2002, 8, 563–574. [Google Scholar] [CrossRef]
- Reichstein, M.; Ciais, P.; Papale, D.; Valentini, R.; Running, S.; Viovy, N.; Cramer, W.; Granier, A.; OgÉE, J.; Allard, V.; et al. Reduction of ecosystem productivity and respiration during the European summer 2003 climate anomaly: A joint flux tower, remote sensing and modelling analysis. Glob. Chang. Biol. 2007, 13, 634–651. [Google Scholar] [CrossRef]
- Friend, A.D.; Arneth, A.; Kiang, N.Y.; Lomas, M.; OgÉE, J.; RÖDenbeck, C.; Running, S.W.; Santaren, J.-D.; Sitch, S.; Viovy, N.; et al. Fluxnet and modelling the global carbon cycle. Glob. Chang. Biol. 2007, 13, 610–633. [Google Scholar] [CrossRef]
- Fu, G.; Shen, Z.X.; Zhang, X.Z.; Shi, P.L.; He, Y.T.; Zhang, Y.J.; Sun, W.; Wu, J.S.; Zhou, Y.T.; Pan, X. Calibration of MODIS-based gross primary production over an alpine meadow on the Tibetan Plateau. Can. J. Remote Sens. 2012, 38, 157–168. [Google Scholar] [CrossRef]
- He, M.; Zhou, Y.; Ju, W.; Chen, J.; Zhang, L.; Wang, S.; Saigusa, N.; Hirata, R.; Murayama, S.; Liu, Y. Evaluation and improvement of MODIS gross primary productivity in typical forest ecosystems of East Asia based on eddy covariance measurements. J. For. Res. 2012, 18, 31–40. [Google Scholar] [CrossRef]
- Kanniah, K.D.; Beringer, J.; Hutley, L.B.; Tapper, N.J.; Zhu, X. Evaluation of collections 4 and 5 of the MODIS gross primary productivity product and algorithm improvement at a tropical savanna site in Northern Australia. Remote Sens. Environ. 2009, 113, 1808–1822. [Google Scholar] [CrossRef]
- Tang, X.; Li, H.; Huang, N.; Li, X.; Xu, X.; Ding, Z.; Xie, J. A comprehensive assessment of MODIS-derived GPP for forest ecosystems using the site-level fluxnet database. Environ. Earth Sci. 2015, 74, 5907–5918. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Maeirsperger, T.K.; Gower, S.T.; Kirschbaum, A.A.; Running, S.W.; Zhao, M.; Wofsy, S.C.; Dunn, A.L.; et al. Site-level evaluation of satellite-based global terrestrial gross primary production and net primary production monitoring. Glob. Chang. Biol. 2005, 11, 666–684. [Google Scholar] [CrossRef]
- Verma, M.; Friedl, M.; Richardson, A.; Kiely, G.; Cescatti, A.; Law, B.; Wohlfahrt, G.; Gielen, B.; Roupsard, O.; Moors, E. Remote sensing of annual terrestrial gross primary productivity from MODIS: An assessment using the fluxnet la thuile data set. Biogeosciences 2014, 11, 2185–2200. [Google Scholar] [CrossRef] [Green Version]
- Verma, M.; Friedl, M.A.; Law, B.E.; Bonal, D.; Kiely, G.; Black, T.A.; Wohlfahrt, G.; Moors, E.J.; Montagnani, L.; Marcolla, B.; et al. Improving the performance of remote sensing models for capturing intra- and inter-annual variations in daily GPP: An analysis using global fluxnet tower data. Agric. For. Meteorol. 2015, 214–215, 416–429. [Google Scholar] [CrossRef]
- Yan, H.; Fu, Y.; Xiao, X.; Huang, H.Q.; He, H.; Ediger, L. Modeling gross primary productivity for winter wheat–maize double cropping system using MODIS time series and CO2 eddy flux tower data. Agric. Ecosyst. Environ. 2009, 129, 391–400. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.-M.; Chen, J.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F.; et al. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Q.; Jiang, J.I.E.; Tang, Y. Calibration of terra/MODIS gross primary production over an irrigated cropland on the north China plain and an alpine meadow on the Tibetan Plateau. Glob. Chang. Biol. 2008, 14, 757–767. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, X.; Ju, W.; Chen, J.M.; Wang, S.; Wang, H.; Yuan, W.; Andrew Black, T.; Jassal, R.; Ibrom, A.; et al. Global parameterization and validation of a two-leaf light use efficiency model for predicting gross primary production across fluxnet sites. J. Geophys. Res. Biogeosci. 2016, 121, 1045–1072. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.H.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. Fluxnet: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Yu, G.R.; Wen, X.F.; Sun, X.M.; Tanner, B.D.; Lee, X.; Chen, J.Y. Overview of chinaflux and evaluation of its eddy covariance measurement. Agric. For. Meteorol. 2006, 137, 125–137. [Google Scholar] [CrossRef]
- Turner, D.P.; Urbanski, S.; Bremer, D.; Wofsy, S.C.; Meyers, T.; Gower, S.T.; Gregory, M. A cross-biome comparison of daily light use efficiency for gross primary production. Glob. Chang. Biol. 2003, 9, 383–395. [Google Scholar] [CrossRef]
- Yang, F.; Ichii, K.; White, M.A.; Hashimoto, H.; Michaelis, A.R.; Votava, P.; Zhu, A.X.; Huete, A.; Running, S.W.; Nemani, R.R. Developing a continental-scale measure of gross primary production by combining MODIS and ameriflux data through support vector machine approach. Remote Sens. Environ. 2007, 110, 109–122. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Rasmussen, M.S.; Stisen, S.; Diouf, A. Evaluation of satellite based primary production modelling in the semi-arid sahel. Remote Sens. Environ. 2006, 105, 173–188. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Masek, J.G.; Rundquist, D.C.; Verma, S.; Suyker, A.; Baker, J.M.; Hatfield, J.L.; Meyers, T. Remote estimation of crop gross primary production with Landsat data. Remote Sens. Environ. 2012, 121, 404–414. [Google Scholar] [CrossRef]
- Wang, C.L.; Zhang, Y.L.; Wang, Z.F.; Bai, W.Q. Analysis of landscape characteristics of the wetland systems in the Lhasa River Basin. Resour. Sci. 2010, 32, 1634–1642. [Google Scholar]
- He, G.Q.; Yang, G.H.; Feng, Y.Z.; Jiang, Y. Analysis on alpine wetlands eco-system structure and function in Tibet Plateau. Agric. Res. Arid Areas 2007, 25, 185–189. [Google Scholar]
- Zhang, Y. Land Use and Land Cover Change and the Climate Change Adaptation in Tibetan Plateau; China Meteorological Press: Beijing, China, 2012. [Google Scholar]
- MODIS Collection 5 Global Subsetting and Visualization Tool. Available online: http://daac.ornl.gov/MODIS (accessed on 12 July 2016).
- Jenkins, J.P.; Richardson, A.D.; Braswell, B.H.; Ollinger, S.V.; Hollinger, D.Y.; Smith, M.L. Refining light-use efficiency calculations for a deciduous forest canopy using simultaneous tower-based carbon flux and radiometric measurements. Agric. For. Meteorol. 2007, 143, 64–79. [Google Scholar] [CrossRef]
- Landsberg, J.J.; Prince, S.D.; Jarvis, P.G.; McMurtrie, R.E.; Luxmoore, R.; Medlyn, B.E. Energy conversion and use in forests: An analysis of forest production in terms of radiation utilisation efficiency (ε). In The Use of Remote Sensing in the Modeling of Forest Productivity; Shimoda, H., Gholz, H.L., Nakane, K., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1997; pp. 273–298. [Google Scholar]
- Fu, G.; Zhang, X.; Zhang, Y.; Shi, P.; Li, Y.; Zhou, Y.; Yang, P.; Shen, Z. Experimental warming does not enhance gross primary production and above-ground biomass in the alpine meadow of Tibet. J. Appl. Remote Sens. 2013, 7, 073505. [Google Scholar] [CrossRef]
- Atlas, R.; Lucchesi, R. File Specific for Geos-Das Celled Output; Goddard Space Flight Center: Greenbelt, MD, USA, 2000. [Google Scholar]
- Li, C.; He, H.L.; Liu, M.; Su, W.; Fu, Y.L.; Zhang, L.M.; Wen, X.F.; Yu, G.R. The design and application of CO2 flux data processing system at chinaflux. Geo-Inf. Sci. 2008, 10, 557–565. [Google Scholar]
- Kaimai, J.C.; Gaynor, J.E. Another look at sonic thermometry. Bound-Lay Meteorol. 1991, 56, 401–410. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Oncley, S.P.; Stage, S.A. Sonic anemometer tilt correction algorithms. Bound-Lay Meteorol. 2001, 99, 127–150. [Google Scholar] [CrossRef]
- Polsenaere, P.; Lamaud, E.; Lafon, V.; Bonnefond, J.M.; Bretel, P.; Delille, B.; Deborde, J.; Loustau, D.; Abril, G. Spatial and temporal CO2 exchanges measured by eddy covariance over a temperate intertidal flat and their relationships to net ecosystem production. Biogeosciences 2012, 9, 249–268. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water-vapor transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Leuning, R. The correct form of the webb, pearman and leuning equation for eddy fluxes of trace gases in steady and non-steady state, horizontally homogeneous flows. Bound-Lay Meteorol. 2006, 123, 263–267. [Google Scholar] [CrossRef]
- Han, G.; Yang, L.; Yu, J.; Wang, G.; Mao, P.; Gao, Y. Environmental controls on net ecosystem CO2 exchange over a reed (Phragmites australis) wetland in the Yellow River delta, China. Estuar. Coasts 2012, 36, 401–413. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, G.; Jia, Q. Annual cycle of CO2 exchange over a reed (Phragmites australis) wetland in Northeast China. Aquat. Bot. 2009, 91, 91–98. [Google Scholar] [CrossRef]
- Reichstein, M.; Tenhunen, J.D.; Roupsard, O.; Ourcival, J.M.; Rambal, S.; Dore, S.; Valentini, R. Ecosystem respiration in two mediterranean evergreen holm oak forests: Drought effects and decomposition dynamics. Funct. Ecol. 2002, 16, 27–39. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, G.; Clement, R.; Dolman, H.; et al. Gap filling strategies for long term energy flux data sets. Agric. For. Meteorol. 2001, 107, 71–77. [Google Scholar] [CrossRef]
- Ruimy, A.; Jarvis, P.G.; Baldocchi, D.D.; Saugier, B. CO2 fluxes over plant canopies and solar radiation: A review. In Advances in Ecological Research; Begon., I.M., Fitter., A.H., Eds.; Academic Press: Cambridge, MA, USA, 1995; Volume 26, pp. 1–68. [Google Scholar]
- Lloyd, J.; Taylor, J.A. On the temperature-dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
- Van’t Hoff, J.H. Über die zunehmende bedeutung der anorganischen chemie. Vortrag, gehalten auf der 70. Versammlung der gesellschaft deutscher naturforscher und rzte zu düsseldorf. Z. Anorg. Chem. 1898, 18, 1–13. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: Critical issues and global evaluation. Glob. Chang. Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- Varlet-Grancher, C.; Bonhomme, R.; Jacob, C.; Artis, P.; Chartier, M. Caracterisation et Evolution de la Structure d'un Couvert Vegetal de Canne a Sucre. Ann. Agron. 1980, 31, 1–26. [Google Scholar]
- Zhang, X.Z.; Zhang, Y.G.; Zhoub, Y.H. Measuring and modelling photosynthetically active radiation in Tibet Plateau during April–October. Agric. For. Meteorol. 2000, 102, 207–212. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, C.; Sun, G.; Band, L.E.; McNulty, S.; Noormets, A.; Zhang, Q.; Zhang, Z. Development of a coupled carbon and water model for estimating global gross primary productivity and evapotranspiration based on eddy flux and remote sensing data. Agric. For. Meteorol. 2016, 223, 116–131. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W.; Nemani, R.R. Sensitivity of moderate resolution imaging spectroradiometer (MODIS) terrestrial primary production to the accuracy of meteorological reanalyses. J. Geophys. Res. Biogeosci. 2006, 111. [Google Scholar] [CrossRef]
- Olofsson, P.; Van Laake, P.E.; Eklundh, L. Estimation of absorbed par across scandinavia from satellite measurements: Part I: Incident par. Remote Sens. Environ. 2007, 110, 252–261. [Google Scholar] [CrossRef]
- Xin, Q.; Broich, M.; Suyker, A.E.; Yu, L.; Gong, P. Multi-scale evaluation of light use efficiency in MODIS gross primary productivity for croplands in the midwestern United States. Agric. For. Meteorol. 2015, 201, 111–119. [Google Scholar] [CrossRef]
- Huang, C.; Li, Y.; Yang, H.; Sun, D.; Yu, Z.; Zhang, Z.; Chen, X.; Xu, L. Detection of algal bloom and factors influencing its formation in taihu lake from 2000 to 2011 by MODIS. Environ. Earth Sci. 2013, 71, 3705–3714. [Google Scholar] [CrossRef]
- Olofsson, P.; Eklundh, L. Estimation of absorbed par across scandinavia from satellite measurements. Part II: Modeling and evaluating the fractional absorption. Remote Sens. Environ. 2007, 110, 240–251. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Rasmussen, M.S. Evaluation of MODIS lai, fapar and the relation between fapar and NDVI in a semi-arid environment using in situ measurements. Remote Sens. Environ. 2004, 91, 490–507. [Google Scholar] [CrossRef]
- Shi, P.L.; Sun, X.M.; Xu, L.L.; Zhang, X.Z.; He, Y.T.; Zhang, D.Q.; Yu, G.R. Net ecosystem CO2 exchange and controlling factors in a steppe—Kobresia meadow on the Tibetan Plateau. Sci. China Ser. D 2006, 49, 207–218. [Google Scholar] [CrossRef]
- Kabacoff, R.I. R in Action, Data Analysis and Graphics with r; Manning Publications Co.: Greenwich, CT, USA, 2011. [Google Scholar]
- Yuan, W.; Cai, W.; Xia, J.; Chen, J.; Liu, S.; Dong, W.; Merbold, L.; Law, B.; Arain, A.; Beringer, J.; et al. Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the lathuile database. Agric. For. Meteorol. 2014, 192–193, 108–120. [Google Scholar] [CrossRef]
- Saito, M.; Kato, T.; Tang, Y. Temperature controls ecosystem CO2 exchange of an alpine meadow on the northeastern Tibetan Plateau. Glob. Chang. Biol. 2009, 15, 221–228. [Google Scholar] [CrossRef]
- Kato, T.; Tang, Y.; Gu, S.; Hirota, M.; Du, M.; Li, Y.; Zhao, X. Temperature and biomass influences on interannual changes in CO2 exchange in an alpine meadow on the Qinghai-Tibetan Plateau. Glob. Chang. Biol. 2006, 12, 1285–1298. [Google Scholar] [CrossRef]
- Alberto, M.C.R.; Wassmann, R.; Hirano, T.; Miyata, A.; Kumar, A.; Padre, A.; Amante, M. CO2/heat fluxes in rice fields: Comparative assessment of flooded and non-flooded fields in the philippines. Agric. For. Meteorol. 2009, 149, 1737–1750. [Google Scholar] [CrossRef]






| GPP * | εmax † (g C MJ−1) | Tmin_max * (°C) | Tmin_min * (°C) | VPDmax * (Kpa) | VPDmin * (Kpa) | FPAR * | Meteorology Data |
|---|---|---|---|---|---|---|---|
| GPP_MOD | 0.68 | 12.02 | −8.00 | 3.50 | 0.65 | FPARM | DAO ‡ |
| GPP_MODR1 | 0.68 | 12.02 | −8.00 | 3.50 | 0.65 | FPARM | Ground measurements |
| GPP_MODR2 | 0.68 | 12.02 | −8.00 | 3.50 | 0.65 | FPARG | Ground measurements |
| GPP_MODR3 | 1.61 (1.33–1.80) † | 12.02 | −8.00 | 3.50 | 0.65 | FPARG | Ground measurements |
| GPP_MODR4 | 1.61 (1.33–1.80) † | 12.02 | −8.00 | 3.50 | 0.65 | FPARM | Ground measurements |
| 2009 (n = 19) | 2010 (n = 18) | 2011 (n = 19) | 2012 (n = 19) | All (n = 75) | |
|---|---|---|---|---|---|
| GPP_EC | 46.91 (±24.45) Da | 45.60 (±19.41) Ca | 37.93 (±20.52) Ca | 40.89 (±20.50) Ca | 40.74 (±22.39) C |
| GPP_MOD | 13.62 (±8.91) Aa | 13.90 (±9.91) Aa | 13.75 (±8.49) Aa | 14.17 (±9.67) Aa | 13.86 (±9.06) A |
| GPP_MODR1 | 10.88 (±4.84) Aa | 10.18 (±4.79) Aa | 11.47 (±5.09) Aa | 11.66 (±4.65) Aa | 10.06 (±4.78) A |
| GPP_MODR2 | 15.94 (±6.55) ABa | 15.40 (±5.83) ABa | 16.18 (±6.65) Aa | 16.49 (±6.12) ABa | 16.01 (±6.19) A |
| GPP_MODR3 | 39.84 (±16.39) CDa | 40.77 (±15.43) Ca | 31.65 (±13.00) BCa | 38.56 (±14.31) Ca | 37.67(±14.96) C |
| GPP_MODR4 | 27.21 (±12.11) BCa | 26.95 (±12.69) Ba | 22.43 (±9.96) ABa | 27.26 (±10.86) BCa | 25.99 (±11.46) B |
| Methods * | RMSE (g C m−2) † | RPE (%) † | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2009 (n = 46) | 2010 (n = 45) | 2011 (n = 46) | 2012 (n = 45) | Mean | 2009 | 2010 | 2011 | 2012 | Mean | |
| GPP_MOD | 2.90 | 2.59 | 2.14 | 2.26 | 2.47 | −70.4 | −72.0 | −63.7 | −65.7 | −68.0 |
| GPP_MODR1 | 3.24 | 2.97 | 2.41 | 2.59 | 2.80 | −75.1 | −77.5 | −69.3 | −70.0 | −73.0 |
| GPP_MODR2 | 2.84 | 2.55 | 2.04 | 2.21 | 2.41 | −63.8 | −66.4 | −56.7 | −57.8 | −61.2 |
| GPP_MODR3 | 1.30 | 0.95 | 0.97 | 0.86 | 1.02 | −9.4 | −11.3 | −15.4 | −1.4 | −9.4 |
| GPP_MODR4 | 2.01 | 1.75 | 1.55 | 1.37 | 1.67 | −37.9 | −40.4 | −39.9 | −29.9 | −37.0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, B.; He, Y.; Zhang, X.; Fu, G.; Shi, P.; Du, M.; Zhang, Y.; Zong, N. Tower-Based Validation and Improvement of MODIS Gross Primary Production in an Alpine Swamp Meadow on the Tibetan Plateau. Remote Sens. 2016, 8, 592. https://doi.org/10.3390/rs8070592
Niu B, He Y, Zhang X, Fu G, Shi P, Du M, Zhang Y, Zong N. Tower-Based Validation and Improvement of MODIS Gross Primary Production in an Alpine Swamp Meadow on the Tibetan Plateau. Remote Sensing. 2016; 8(7):592. https://doi.org/10.3390/rs8070592
Chicago/Turabian StyleNiu, Ben, Yongtao He, Xianzhou Zhang, Gang Fu, Peili Shi, Mingyuan Du, Yangjian Zhang, and Ning Zong. 2016. "Tower-Based Validation and Improvement of MODIS Gross Primary Production in an Alpine Swamp Meadow on the Tibetan Plateau" Remote Sensing 8, no. 7: 592. https://doi.org/10.3390/rs8070592
APA StyleNiu, B., He, Y., Zhang, X., Fu, G., Shi, P., Du, M., Zhang, Y., & Zong, N. (2016). Tower-Based Validation and Improvement of MODIS Gross Primary Production in an Alpine Swamp Meadow on the Tibetan Plateau. Remote Sensing, 8(7), 592. https://doi.org/10.3390/rs8070592