A One-Source Approach for Estimating Land Surface Heat Fluxes Using Remotely Sensed Land Surface Temperature
Abstract
:1. Introduction
2. Model Description
2.1. Theoretical Background of One-Source Model
2.2. Development of One-Source Model for Land (OSML)
2.3. Surface Energy Balance System (SEBS)
3. Study Area and Data Processing
3.1. SMACEX Campaign
3.1.1. Description of SMACEX Campaign Area and Related Experiment SMACEX
3.1.2. Remotely Sensed and In-Situ Observations Required for OSML Input over SMACEX
3.1.3. Eddy Covariance System Measurements over SMACEX
3.2. Hiwater-MUSOEXE Experiment
3.2.1. Description of HiWATER-MUSOEXE Campaign
3.2.2. Site Measurements and Remotely Sensed Data for OSML Input over MUSOEXE
4. Results
4.1. Validation at SMACEX Site
4.1.1. Validation with Tower-Based Observations
4.1.2. Spatial Distribution of Surface Heat Fluxes
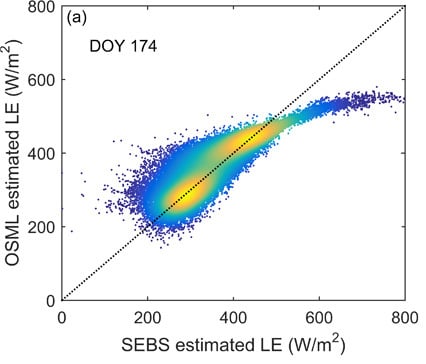
4.1.3. Intercomparison of Radiometric-Convective Resistance Derived from OSML and SEBS
4.2. Validation at HiWATER-MUSOEXE Site
4.2.1. Validation with Tower-based Observations
4.2.2. Spatial Patterns of Estimated Regional Land Surface Heat Fluxes
5. Discussion
5.1. Advantages of OSML over Typical One-Source Models
5.2. Discussion on Different Approaches to Mediate Difference between LST and Taero
5.3. Operationality of OSML
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Estimation of rae in OSML
References
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History, and Applications; Springer: New York, NY, USA, 1982. [Google Scholar]
- Brutsaert, W. Hydrology: An Introduction; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Hwang, K.; Choi, M.; Lee, S.O.; Seo, J.W. Estimation of instantaneous and daily net radiation from MODIS data under clear sky conditions: A case study in East Asia. Irrig. Sci. 2012, 31, 1173–1184. [Google Scholar] [CrossRef]
- Kabat, P. Vegetation, Water, Humans and the Climate: A New Perspective on an Internactive System; Springer: New York, NY, USA, 2004. [Google Scholar]
- Katul, G.G.; Oren, R.; Manzoni, S.; Higgins, C.; Parlange, M.B. Evapotranspiration: A process driving mass transport and energy exchange in the soil-plant-atmosphere-climate system. Rev. Geophys. 2012. [Google Scholar] [CrossRef]
- Eagleson, P.S. Ecohydrology: Darwinian Expression of Vegetation Form and Function; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Petropoulos, G. Remote Sensing of Land Surface Turbulent Fluxes and Soil Moisture: State of the Art; Taylor & Francis: Abingdon, UK, 2013; pp. 224–250. [Google Scholar]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Hirschboeck, K.K.; Brown, P. Integrating remote sensing and ground methods to estimate evapotranspiration. Crit. Rev. Plant Sci. 2007, 26, 139–168. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, R.L.; Wan, Z.M.; Bi, Y.Y.; Zhou, C.H.; Tang, B.H.; Yan, G.J.; Zhang, X.Y. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef] [PubMed]
- Jiménez, C.; Prigent, C.; Mueller, B.; Seneviratne, S.; Mc-Cabe, M.; Wood, E.; Rossow, W.; Balsamo, G.; Betts, A.; Dirmeyer, P. Global intercomparison of 12 land surface heat flux estimates. J. Geophys. Res. 2011, 116, 1–27. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.Z.; Zhao, M.S.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Mueller, B.; Hirschi, M.; Jimenez, C.; Ciais, P.; Dirmeyer, P.A.; Dolman, A.J.; Fisher, J.B.; Jung, M.; Ludwig, F.; Maignan, F.; et al. Benchmark products for land evapotranspiration: Landflux-eval multi-data set synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 3707–3720. [Google Scholar] [CrossRef]
- Mueller, B.; Seneviratne, S.; Jimenez, C.; Corti, T.; Hirschi, M.; Balsamo, G.; Ciais, P.; Dirmeyer, P.; Fisher, J.; Guo, Z. Evaluation of global observations-based evapotranspiration datasets and IPCC AR4 simulations. Geophys. Res. Lett. 2011, 38, 1–7. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Leuning, R.; Chiew, F.H.S.; Wang, E.L.; Zhang, L.; Liu, C.M.; Sun, F.B.; Peel, M.C.; Shen, Y.J.; Jung, M. Decadal trends in evaporation from global energy and water balances. J. Hydrometeorol. 2012, 13, 379–391. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.L. Surface temperature and emissivity at various scales: Definition, measurement and related problems. Remote Sens. Rev. 1995, 12, 225–253. [Google Scholar] [CrossRef]
- Boulet, G.; Olioso, A.; Ceschia, E.; Marloie, O.; Coudert, B.; Rivalland, V.; Chirouze, J.; Chehbouni, G. An empirical expression to relate aerodynamic and surface temperatures for use within single-source energy balance models. Agric. For. Meteorol. 2012, 161, 148–155. [Google Scholar] [CrossRef] [Green Version]
- Chehbouni, A.; Seen, D.L.; Njoku, E.; Monteny, B. Examination of the difference between radiative and aerodynamic surface temperatures over sparsely vegetated surfaces. Remote Sens. Environ. 1996, 58, 177–186. [Google Scholar] [CrossRef]
- Lhomme, J.-P.; Chehbouni, A.; Monteny, B. Sensible heat flux-radiometric surface temperature relationship over sparse vegetation: Parameterizing b-1. Bound. Layer Meteorol. 2000, 97, 431–457. [Google Scholar] [CrossRef]
- Matsushima, D. Relations between aerodynamic parameters of heat transfer and thermal-infrared thermometry in the bulk surface formulation. J. Meterol. Soc. Jpn. 2005, 83, 373–389. [Google Scholar] [CrossRef]
- Stewart, J.B.; Kustas, W.P.; Humes, K.S.; Nichols, W.D.; Moran, M.S.; De Bruin, H. Sensible heat flux-radiometric surface temperature relationship for eight semiarid areas. J. Appl. Meteorol. 1994, 33, 1110–1117. [Google Scholar] [CrossRef]
- Paul, G.; Gowda, P.H.; Prasad, P.V.; Howell, T.A.; Aiken, R.M.; Neale, C.M. Investigating the influence of roughness length for heat transport (zoh) on the performance of SEBAL in semi-arid irrigated and dryland agricultural systems. J. Hydrol. 2014, 509, 231–244. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System(SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. Discuss. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface-temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and the Two-source Energy Balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
- Gokmen, M.; Vekerdy, Z.; Verhoef, A.; Verhoef, W.; Batelaan, O.; Van der Tol, C. Integration of soil moisture in sebs for improving evapotranspiration estimation under water stress conditions. Remote Sens. Environ. 2012, 121, 261–274. [Google Scholar] [CrossRef]
- Kustas, W.P.; Choudhury, B.J.; Moran, M.S.; Reginato, R.J.; Jackson, R.D.; Gay, L.W.; Weaver, H.L. Determination of sensible heat flux over sparse canopy using thermal infrared data. Agric. For. Meteorol. 1989, 44, 197–216. [Google Scholar] [CrossRef]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst. 2005, 19, 223–249. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Thomsen, A. Evaluating evapotranspiration rates and surface conditions using landsat tm to estimate atmospheric resistance and surface resistance. Remote Sens. Environ. 2002, 79, 329–343. [Google Scholar] [CrossRef]
- Allen, R.G.; Trezza, R.; Kilic, A.; Tasumi, M.; Li, H. Sensitivity of landsat-scale energy balance to aerodynamic variability in mountains and complex terrain. J. Am. Water Resour. Assoc. 2013, 49, 592–604. [Google Scholar] [CrossRef]
- Santos, C.; Lorite, I.; Allen, R.; Tasumi, M. Aerodynamic parameterization of the satellite-based energy balance (METRIC) model for et estimation in rainfed olive orchards of Andalusia, Spain. Water Resour. Manag. 2012, 26, 3267–3283. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. A Two-source Trapezoid Model for Evapotranspiration (TTME) from satellite imagery. Remote Sens. Environ. 2012, 121, 370–388. [Google Scholar] [CrossRef]
- Lu, J.; Tang, R.; Tang, H.; Li, Z.L. A new parameterization scheme for estimating surface energy fluxes with continuous surface temperature, air temperature, and surface net radiation measurements. Water Resour. Res. 2014, 50, 1245–1259. [Google Scholar] [CrossRef]
- Zhang, R.H.; Sun, X.M.; Wang, W.M.; Xu, J.P.; Zhu, Z.L.; Tian, J. An operational two-layer remote sensing model to estimate surface flux in regional scale: Physical background. Sci. China Ser. D 2005, 48, 225–244. [Google Scholar]
- Jiang, L.; Islam, S. Estimation of surface evaporation map over southern great plains using remote sensing data. Water Resour. Res. 2001, 37, 329–340. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.N.; Wooster, M.J.; Islam, S. A review of Ts/Vi remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Norgaard, A.; Fensholt, R.; Jensen, K.H. Combining the triangle method with thermal inertia to estimate regional evapotranspiration-applied to MSG-SEVIRI data in the senegal river basin. Remote Sens. Environ. 2008, 112, 1242–1255. [Google Scholar] [CrossRef]
- Tang, R.L.; Li, Z.L.; Tang, B.H. An application of the Ts/Vi triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in and and semi-arid regions: Implementation and validation. Remote Sens. Environ. 2010, 114, 540–551. [Google Scholar] [CrossRef]
- Wang, K.C.; Li, Z.Q.; Cribb, M. Estimation of evaporative fraction from a combination of day and night land surface temperatures and NDVI: A new method to determine the priestley-taylor parameter. Remote Sens. Environ. 2006, 102, 293–305. [Google Scholar] [CrossRef]
- Yang, Y.; Su, H.; Zhang, R.; Tian, J.; Li, L. An Enhanced Two-source Evapotranspiration Model for Land (ETEML): Algorithm and evaluation. Remote Sens. Environ. 2015, 168, 54–65. [Google Scholar] [CrossRef]
- Mallick, K.; Jarvis, A.J.; Boegh, E.; Fisher, J.B.; Drewry, D.T.; Tu, K.P.; Hook, S.J.; Hulley, G.; Ardö, J.; Beringer, J. A Surface Temperature Initiated Closure (STIC) for surface energy balance fluxes. Remote Sens. Environ. 2014, 141, 243–261. [Google Scholar] [CrossRef]
- Choudhury, B.; Idso, S.; Reginato, R. Analysis of an empirical model for soil heat flux under a growing wheat crop for estimating evaporation by an infrared-temperature based energy balance equation. Agric. For. Meteorol. 1987, 39, 283–297. [Google Scholar] [CrossRef]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Henderson-Sellers, A.; Rosenzweig, C.; Sellers, P.J. Evapotranspiration models with canopy resistance for use in climate models, a review. Agric. For. Meteorol. 1991, 54, 373–388. [Google Scholar] [CrossRef]
- Jarvis, P. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Noilhan, J.; Planton, S. A simple parameterization of land surface processes for meteorological models. Mon. Weather Rev. 1989, 117, 536–549. [Google Scholar] [CrossRef]
- Sellers, P.; Mintz, Y.; Sud, Y.E.A.; Dalcher, A. A Simple Biosphere Model (SIB) for use within general circulation models. J. Atmos. Sci. 1986, 43, 505–531. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Vail, L.W.; Lettenmaier, D.P. A distributed hydrology-vegetation model for complex terrain. Water Resour. Res. 1994, 30, 1665–1679. [Google Scholar] [CrossRef]
- Su, Z.; Schmugge, T.; Kustas, W.; Massman, W. An evaluation of two models for estimation of the roughness height for heat transfer between the land surface and the atmosphere. J. Appl. Meteorol. 2001, 40, 1933–1951. [Google Scholar] [CrossRef]
- Kustas, W.P.; Hatfield, J.L.; Prueger, J.H. The Soil Moisture-Atmosphere Coupling Experiment (SMACEX): Background, hydrometeorological conditions, and preliminary findings. J. Hydrometeorol. 2005, 6, 791–804. [Google Scholar] [CrossRef]
- Choi, M.; Kustas, W.P.; Anderson, M.C.; Allen, R.G.; Li, F.Q.; Kjaersgaard, J.H. An intercomparison of three remote sensing-based surface energy balance algorithms over a corn and soybean production region (Iowa, US) during smacex. Agric. For. Meteorol. 2009, 149, 2082–2097. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prueger, J.H.; Anderson, M.C.; Li, F. A comparison of operational remote sensing-based models for estimating crop evapotranspiration. Agric. For. Meteorol. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]
- Li, F.; Jackson, T.J.; Kustas, W.P.; Schmugge, T.J.; French, A.N.; Cosh, M.H.; Bindlish, R. Deriving land surface temperature from Landsat 5 and 7 during SMEX02/SMACEX. Remote Sens. Environ. 2004, 92, 521–534. [Google Scholar] [CrossRef]
- Li, F.Q.; Kustas, W.P.; Prueger, J.H.; Neale, C.M.U.; Jackson, T.J. Utility of remote sensing-based two-source energy balance model under low- and high-vegetation cover conditions. J. Hydrometeorol. 2005, 6, 878–891. [Google Scholar] [CrossRef]
- Tasumi, M.; Allen, R.G.; Trezza, R. At-surface reflectance and albedo from satellite for operational calculation of land surface energy balance. J. Hydrol. Eng. 2008, 13, 51–63. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-based energy balance for Mapping Evapotranspiration with Internalized Calibration (METRIC) - applications. J. Irrig. Drain Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Anderson, M.C.; Neale, C.M.U.; Li, F.; Norman, J.M.; Kustas, W.P.; Jayanthi, H.; Chavez, J. Upscaling ground observations of vegetation water content, canopy height, and leaf area index during SMEX02 using aircraft and landsat imagery. Remote Sens. Environ. 2004, 92, 447–464. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef] [PubMed]
- Foken, T.; Wimmer, F.; Mauder, M.; Thomas, C.; Liebethal, C. Some aspects of the energy balance closure problem. Atmos. Chem. Phys. 2006, 6, 4395–4402. [Google Scholar] [CrossRef]
- Leuning, R.; van Gorsel, E.; Massman, W.J.; Isaac, P.R. Reflections on the surface energy imbalance problem. Agric. For. Meteorol. 2012, 156, 65–74. [Google Scholar] [CrossRef]
- Su, H.B.; McCabe, M.F.; Wood, E.F.; Su, Z.; Prueger, J.H. Modeling evapotranspiration during smacex: Comparing two approaches for local- and regional-scale prediction. J. Hydrometeorol. 2005, 6, 910–922. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Prueger, J.H.; Hatfield, J.L.; Kustas, W.P.; Hipps, L.E.; MacPherson, J.I.; Neale, C.M.U.; Eichinger, W.E.; Cooper, D.I.; Parkin, T.B. Tower and aircraft eddy covariance measurements of water vapor, energy, and carbon dioxide fluxes during smacex. J. Hydrometeorol. 2005, 6, 954–960. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y. Heihe watershed allied telemetry experimental research (hiwater): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the hiwater-musoexe. J. Geophys. Res. Atmos. 2013. [Google Scholar] [CrossRef]
- Yang, K.; Wang, J. A temperature prediction-correction method for estimating surface soil heat flux from soil temperature and moisture data. Sci. China Ser. D Earth Sci. 2008, 51, 721–729. [Google Scholar] [CrossRef]
- Li, H.; Sun, D.; Yu, Y.; Wang, H.; Liu, Y.; Liu, Q.; Du, Y.; Wang, H.; Cao, B. Evaluation of the VIIRS and Modis lst products in an arid area of Northwest China. Remote Sens. Environ. 2014, 142, 111–121. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Tonooka, H. Accurate atmospheric correction of ASTER thermal infrared imagery using the WVS method. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2778–2792. [Google Scholar] [CrossRef]
- Sun, C.; Liu, Q.; Wen, J. An algorithm for retrieving land surface albedo from HJ-1 CCD data. Remote Sens. Land Resour. 2013, 25, 58–63. [Google Scholar]
- Yang, Y.; Long, D.; Guan, H.; Liang, W.; Simmons, C.; Batelaan, O. Comparison of three dual-source remote sensing evapotranspiration models during the musoexe-12 campaign: Revisit of model physics. Water Resour. Res. 2015. [Google Scholar] [CrossRef]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing Surface Energy Balance Algorithm for Land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Huang, C.; Li, Y.; Gu, J.; Lu, L.; Li, X. Improving estimation of evapotranspiration under water-limited conditions based on sebs and MODIS data in arid regions. Remote Sens. 2015, 7, 16795–16814. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, S.; Zhang, F.; Zhou, J.; Jia, Z.; Song, L. Estimations of regional surface energy fluxes over heterogeneous oasis–desert surfaces in the middle reaches of the Heihe River during hiwater-musoexe. IEEE Trans. Geosci. Remote Sens. 2015, 12, 671–675. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Li, F.Q.; Prueger, J.H.; Mecikalski, J.R. Effects of vegetation clumping on two-source model estimates of surface energy fluxes from an agricultural landscape during smacex. J. Hydrometeorol. 2005, 6, 892–909. [Google Scholar] [CrossRef]
- Chavez, J.L.; Neale, C.M.U.; Hipps, L.E.; Prueger, J.H.; Kustas, W.P. Comparing aircraft-based remotely sensed energy balance fluxes with eddy covariance tower data using heat flux source area functions. J. Hydrometeorol. 2005, 6, 923–940. [Google Scholar] [CrossRef]
- French, A.N.; Jacob, F.; Anderson, M.C.; Kustas, W.P.; Timmermans, W.; Gieske, A.; Su, Z.; Su, H.; McCabe, M.F.; Li, F.; et al. Surface energy fluxes with the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) at the Iowa 2002 smacex site (USA). Remote Sens. Environ. 2005, 99, 471. [Google Scholar] [CrossRef]
- Yang, Y.T.; Shang, S.H. A hybrid dual-source scheme and trapezoid framework-based evapotranspiration model (HTEM) using satellite images: Algorithm and model test. J. Geophys. Res. Atmos. 2013, 118, 2284–2300. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Suyker, A.E.; Wen, X. Influence of leaf area index on the radiometric resistance to heat transfer. Bound. Layer Meteorol. 2016, 158, 105–123. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K. Merra: Nasa’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Jambor, U.E.A.; Gottschalck, J.; Mitchell, K.; Meng, C.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Shi, C.; Jiang, L.; Zhang, T.; Xu, B.; Han, S. Status and plans of CMA Land Data Assimilation System (CLDAS) project. In Proceedings of the EGU General Assembly 2014, Vienna, Austria, 27 April–2 May 2014.














| OSML | SEBS | |||
|---|---|---|---|---|
| DOY174 | DOY182 | DOY174 | DOY182 | |
| Meteorological Forcing | ||||
| Incoming solar radiation (W/m2) | 834 | 859 | 834 | 859 |
| Air temperature (°C) | 29.6 | 29.35 | 29.6 | 29.35 |
| Vapor Pressure (kPa) | 1.96 | 2.2 | 1.96 | 2.2 |
| Atmospheric pressure (kPa) | 98.2 | 98.2 | 98.2 | 98.2 |
| Wind speed (m/s) | × | × | 6.3 | 5.32 |
| Satellite-Based Retrievals | ||||
| LST | Derived from TIR, band 6 based on Li et al. [55] | |||
| LAI | Empirical relationship given by Anderson et al. [60] | |||
| NDVI | Calculated with NIR and RED band | |||
| Land cover | Obtained from the National Snow and Ice Data Center (http://nsidc.org/index.html) | |||
| Vegetation Fractional Cover | Estimated from NDVI | |||
| Albedo | Albedo was retrieved from the visible and near-infrared bands (1–5, 7) of the Landsat images following Tasumi et al. [57] | |||
| Crop height (m) | × | × | Empirical relationship given by Anderson et al. [60] | |
| Surface roughness (m) | × | × | 0.1 × Crop height | |
| Displacement height (m) | × | × | 0.67 × Crop height | |
| Flux | OSML | SEBS | ||||
|---|---|---|---|---|---|---|
| Component | Bias | MAD | RMSD | Bias | MAD | RMSD |
| Rn | 7.3 | 18.5 | 24.0 | 7.3 | 18.5 | 24.0 |
| G | −6.9 | 20.1 | 23.3 | −6.9 | 20.1 | 23.3 |
| LE | 23.5 | 39.6 | 46.5 | 51.2 | 74.2 | 83.2 |
| H | −18.4 | 30.2 | 34.5 | −41.6 | 58.0 | 69.2 |
| DOY174 | DOY182 | |||||
|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | |||
| LE | OSML | Regional | 390.6 | 83.0 | 386.8 | 92.3 |
| Corn | 425.4 | 59.1 | 450.5 | 62.2 | ||
| Soybean | 313.8 | 61.0 | 303.3 | 56.6 | ||
| SEBS | Regional | 387.9 | 107.8 | 413.4 | 114.0 | |
| Corn | 411.0 | 104.7 | 470.2 | 103.4 | ||
| Soybean | 324.8 | 68.3 | 344.1 | 76.8 | ||
| H | OSML | Regional | 93.9 | 55.2 | 117.6 | 57.5 |
| Corn | 78.1 | 39.2 | 84.4 | 38.6 | ||
| Soybean | 146.7 | 42.9 | 175.7 | 38.8 | ||
| SEBS | Regional | 95.7 | 83.6 | 101.9 | 75.0 | |
| Corn | 91.6 | 87.6 | 74.9 | 75.3 | ||
| Soybean | 135.3 | 47.8 | 139.0 | 53.2 | ||
| DOY174 | DOY182 | ||
|---|---|---|---|
| Mean | Mean | ||
| rae_OSML | Corn | 51.8 | 43.6 |
| Soybean | 52.3 | 48.5 | |
| rae_SEBS | Corn | 47.5 | 56.0 |
| Soybean | 60.4 | 65.0 | |
| Flux | OSML | SEBS | ||||
|---|---|---|---|---|---|---|
| Component | Bias | MAD | RMSD | Bias | MAD | RMSD |
| Rn | −0.2 | 20.8 | 27.8 | −1.6 | 20.3 | 27.8 |
| G | −23.5 | 33.3 | 38.6 | −4.5 | 26.2 | 42.5 |
| LE | 11.8 | 50.4 | 67.0 | 24.5 | 51.8 | 67.8 |
| H | 13.0 | 36.5 | 50.1 | −23.3 | 49.4 | 57.4 |
| DOY 192 | DOY 215 | DOY 231 | ||||
|---|---|---|---|---|---|---|
| LE | H | LE | H | LE | H | |
| Bias | 24.4 | −0.5 | 36.0 | −13.1 | 28.1 | −21.1 |
| MAD | 33.8 | 12.9 | 47.0 | 16.8 | 43.4 | 21.4 |
| RMSD | 38.3 | 21.0 | 49.5 | 19.6 | 47.1 | 22.6 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Qiu, J.; Su, H.; Bai, Q.; Liu, S.; Li, L.; Yu, Y.; Huang, Y. A One-Source Approach for Estimating Land Surface Heat Fluxes Using Remotely Sensed Land Surface Temperature. Remote Sens. 2017, 9, 43. https://doi.org/10.3390/rs9010043
Yang Y, Qiu J, Su H, Bai Q, Liu S, Li L, Yu Y, Huang Y. A One-Source Approach for Estimating Land Surface Heat Fluxes Using Remotely Sensed Land Surface Temperature. Remote Sensing. 2017; 9(1):43. https://doi.org/10.3390/rs9010043
Chicago/Turabian StyleYang, Yongmin, Jianxiu Qiu, Hongbo Su, Qingmei Bai, Suhua Liu, Lu Li, Yilei Yu, and Yaoxian Huang. 2017. "A One-Source Approach for Estimating Land Surface Heat Fluxes Using Remotely Sensed Land Surface Temperature" Remote Sensing 9, no. 1: 43. https://doi.org/10.3390/rs9010043
APA StyleYang, Y., Qiu, J., Su, H., Bai, Q., Liu, S., Li, L., Yu, Y., & Huang, Y. (2017). A One-Source Approach for Estimating Land Surface Heat Fluxes Using Remotely Sensed Land Surface Temperature. Remote Sensing, 9(1), 43. https://doi.org/10.3390/rs9010043