Hashing Based Hierarchical Feature Representation for Hyperspectral Imagery Classification
Abstract
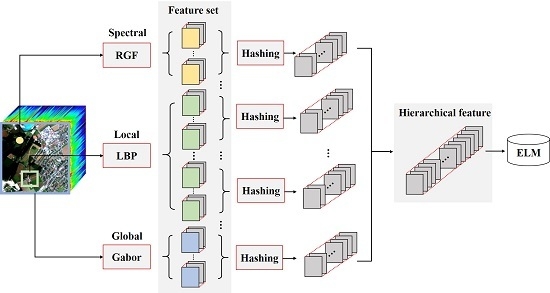
:1. Introduction
2. Based Classification
2.1. Multiple Features Extraction
2.1.1. RGF
2.1.2. LBP
2.1.3. Gabor Filters
2.2. Hashing Based Hierarchical Feature Representation
2.2.1. Step 1
2.2.2. Step 2
2.2.3. Step 3
2.3. ELM Based Classification
| Algorithm 1 The based HSI classification method |
| Input: HSI data, ground truth |
| Initialize: training set, testing set |
| Multiple Features Extraction |
| 1. RGF features based on Equations (1) and (2) |
| 2. LBP features based on Equations (4) |
| 3. Gabor features based on Equations (5) and (6) |
| 4. Feature set generation |
| Hashing based Hierarchical Features |
| 5. Separate the feature set into uniform subsets |
| 6. For 1: Number of subsets |
| Hierarchical feature extraction by Equations (7) and (8) |
| End for |
| 7. Final features generation by Equation (9) |
| ELM based Classification |
| 8. Train ELM by Equations (10) and (11) |
| 9. Classification by ELM |
| Output: Classification results |
3. Experiments and Discussion
3.1. Experimental Setups
3.2. Data Sets
- Indian Pines: This data is widely used in HSI classification, which was gathered by airborne visible/infrared imaging spectrometer (AVIRIS) in Northwestern Indiana. It covers the wavelengths ranges from 0.4 to 2.5 μm with 20 m spatial resolution. In total, pixels are included and 10,249 of them are labeled. The labeled pixels are classified into 16 classes. There are 200 bands available after removing the water absorption channels. A false color composite image (R-G-B=band 36-17-11) and the corresponding ground truth are shown in Figure 3a,b.
- KSC: It is acquired by AVIRIS over the Kennedy Space Center, Florida, on March, 1996. It has 18 m spatial resolution with pixels size and 10 nm spectral resolution with center wavelengths from 400 to 2500 nm. In addition, 176 bands could be used for analysis after removing water absorption and low SNR bands. There are 5211 labeled pixels available that are divided into 16 classes. A false color composite image (R-G-B=band 28-9-10) and the corresponding ground truth are shown in Figure 3c,d.
- GRSS_DFC_2014: This is a challenging HSI data set covering an urban area near Thetford Mines in Québec, Canada, and it is used in the 2014 IEEE GRSS Data Fusion Contest. It was acquired by an airborne long-wave infrared hyperspectral imager with 84 channels ranging between 7.8 to 11.5 μm wavelengths. The size of this data set is pixels, and the spatial resolution is about 1 m. In total, 22,532 labeled pixels and a ground truth with seven land cover classes are provided. Some research has indicated that this data set is more challenging for HSI classification [61]. A false color composite image (R-G-B=band 30-45-66) and the corresponding ground truth are shown in Figure 3e,f.
3.3. Classification Results
3.3.1. Results on Indian Pines Data Set
3.3.2. Results on KSC Data Set
3.3.3. Results on GRSS_DFC_2014 Data Set
3.4. Analysis and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fu, Y.; Zhao, C.; Wang, J.; Jia, X.; Yang, G.; Song, X.; Feng, H. An Improved Combination of Spectral and Spatial Features for Vegetation Classification in Hyperspectral Images. Remote Sens. 2017, 9, 261. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; An, Z.; Jiang, Z.; Ma, Y. A Novel Spectral-Unmixing-Based Green Algae Area Estimation Method for GOCI Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 437–449. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, X.; Li, S.; Li, K.; Li, J.; Benediktsson, J.A. Hyperspectral Anomaly Detection With Attribute and Edge-Preserving Filters. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5600–5611. [Google Scholar] [CrossRef]
- Xu, X.; Shi, Z. Multi-objective based spectral unmixing for hyperspectral images. ISPRS J. Photogramm. Remote Sens. 2017, 124, 54–69. [Google Scholar] [CrossRef]
- Zhong, P.; Zhang, P.; Wang, R. Dynamic Learning of SMLR for Feature Selection and Classification of Hyperspectral Data. IEEE Geosci. Remote Sens. Lett. 2008, 5, 280–284. [Google Scholar] [CrossRef]
- Gomez-Chova, L.; Camps-Valls, G.; Munoz-Mari, J.; Calpe, J. Semisupervised Image Classification with Laplacian Support Vector Machines. IEEE Geosci. Remote Sens. Lett. 2008, 5, 336–340. [Google Scholar] [CrossRef]
- Pal, M.; Foody, G.M. Feature Selection for Classification of Hyperspectral Data by SVM. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2297–2307. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Castrodad, A.; Xing, Z.; Greer, J.B.; Bosch, E.; Carin, L.; Sapiro, G. Learning discriminative sparse representations for modeling, source separation, and mapping of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4263–4281. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral-spatial hyperspectral image segmentation using subspace multinomial logistic regression and Markov random fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E. Hyperspectral image classification using Gaussian mixture models and Markov random fields. IEEE Geosci. Remote Sens. Lett. 2014, 11, 153–157. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Fauvel, M.; Chanussot, J.; Benediktsson, J.A. SVM-and MRF-based method for accurate classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 736–740. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Atli Benediktsson, J.; Waske, B.; Bruzzone, L. Extended profiles with morphological attribute filters for the analysis of hyperspectral data. Int. J. Remote Sens. 2010, 31, 5975–5991. [Google Scholar] [CrossRef]
- Zhong, Z.; Fan, B.; Ding, K.; Li, H.; Xiang, S.; Pan, C. Efficient Multiple Feature Fusion With Hashing for Hyperspectral Imagery Classification: A Comparative Study. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4461–4478. [Google Scholar] [CrossRef]
- Li, J.; Marpu, P.R.; Plaza, A.; Bioucas-Dias, J.M.; Benediktsson, J.A. Generalized composite kernel framework for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4816–4829. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, T.; Jia, X.; Benediktsson, J.A.; Chanussot, J. Nonlinear multiple kernel learning with multiple-structure-element extended morphological profiles for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3235–3247. [Google Scholar] [CrossRef]
- Liu, T.; Gu, Y.; Jia, X.; Benediktsson, J.A.; Chanussot, J. Class-Specific Sparse Multiple Kernel Learning for Spectral–Spatial Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7351–7365. [Google Scholar] [CrossRef]
- Wang, Q.; Gu, Y.; Tuia, D. Discriminative multiple kernel learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3912–3927. [Google Scholar] [CrossRef]
- Zhang, Q.; Tian, Y.; Yang, Y.; Pan, C. Automatic Spatial–Spectral Feature Selection for Hyperspectral Image via Discriminative Sparse Multimodal Learning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 261–279. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Du, B.; Huang, X.; Tang, Y.Y.; Tao, D. Simultaneous Spectral-Spatial Feature Selection and Extraction for Hyperspectral Images. IEEE Trans. Cybern. 2017, PP, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X. On Combining Multiple Features for Hyperspectral Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 879–893. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X. A modified stochastic neighbor embedding for multi-feature dimension reduction of remote sensing images. ISPRS J. Photogramm. Remote Sens. 2013, 83, 30–39. [Google Scholar] [CrossRef]
- Wang, M.; Yu, J.; Niu, L.; Sun, W. Feature Extraction for Hyperspectral Images Using Low-Rank Representation With Neighborhood Preserving Regularization. IEEE Geosci. Remote Sens. Lett. 2017, 14, 836–840. [Google Scholar]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Pal, M. Ensemble of support vector machines for land cover classification. Int. J. Remote Sens. 2008, 29, 3043–3049. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. An SVM ensemble approach combining spectral, structural, and semantic features for the classification of high-resolution remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 257–272. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, B.; He, X.; Qiu, Q.; Liu, F. Class-Specific Random Forest With Cross-Correlation Constraints for Spectral–Spatial Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 257–261. [Google Scholar] [CrossRef]
- Xia, J.; Bombrun, L.; Adalı, T.; Berthoumieu, Y.; Germain, C. Spectral–spatial classification of hyperspectral images using ica and edge-preserving filter via an ensemble strategy. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4971–4982. [Google Scholar] [CrossRef]
- Xia, J.; Falco, N.; Benediktsson, J.A.; Du, P.; Chanussot, J. Hyperspectral Image Classification With Rotation Random Forest Via KPCA. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1601–1609. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Wang, R. Using stacked generalization to combine SVMs in magnitude and shape feature spaces for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2193–2205. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. Hierarchical Guidance Filtering-Based Ensemble Classification for Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4177–4189. [Google Scholar] [CrossRef]
- Debes, C.; Merentitis, A.; Heremans, R.; Hahn, J.; Frangiadakis, N.; Kasteren, T.V.; Liao, W.; Bellens, R.; Pižurica, A.; Gautama, S. Hyperspectral and LiDAR Data Fusion: Outcome of the 2013 GRSS Data Fusion Contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2405–2418. [Google Scholar] [CrossRef]
- Liao, W.; Pižurica, A.; Bellens, R.; Gautama, S.; Philips, W. Generalized Graph-Based Fusion of Hyperspectral and LiDAR Data Using Morphological Features. IEEE Geosci. Remote Sens. Lett. 2015, 12, 552–556. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Zhang, N.; Xie, S. Hyperspectral Image Classification Based on Nonlinear Spectral–Spatial Network. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1782–1786. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. R-VCANet: A new deep-learning-based hyperspectral image classification method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1975–1986. [Google Scholar] [CrossRef]
- Wu, H.; Prasad, S. Convolutional Recurrent Neural Networks for Hyperspectral Data Classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef]
- Ding, C.; Li, Y.; Xia, Y.; Wei, W.; Zhang, L.; Zhang, Y. Convolutional Neural Networks Based Hyperspectral Image Classification Method with Adaptive Kernels. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Zhong, P.; Gong, Z.; Li, S.; Schonlieb, C.B. Learning to Diversify Deep Belief Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Liang, H.; Li, Q. Hyperspectral Imagery Classification Using Sparse Representations of Convolutional Neural Network Features. Remote Sens. 2016, 8, 99. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Zhang, Q.; Shen, X.; Xu, L.; Jia, J. Rolling Guidance Filter. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 815–830. [Google Scholar]
- Li, W.; Chen, C.; Su, H.; Du, Q. Local Binary Patterns and Extreme Learning Machine for Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Gabor-Filtering-Based Nearest Regularized Subspace for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1012–1022. [Google Scholar] [CrossRef]
- Xu, X.; Shi, Z.; Pan, B. A New Unsupervised Hyperspectral Band Selection Method Based on Multiobjective Optimization. IEEE Geosci. Remote Sens. Lett. 2017, PP, 1–5. [Google Scholar] [CrossRef]
- Cavallaro, G.; Falco, N.; Mura, M.D.; Benediktsson, J.A. Automatic Attribute Profiles. IEEE Trans. Image Process. 2017, 26, 1859–1872. [Google Scholar]
- Kang, X.; Xiang, X.; Li, S.; Benediktsson, J.A. PCA-Based Edge-Preserving Features for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, PP, 1–12. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Samat, A.; Du, P.; Liu, S.; Li, J.; Cheng, L. E2LMs : Ensemble Extreme Learning Machines for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1060–1069. [Google Scholar] [CrossRef]
- Su, H.; Cai, Y.; Du, Q. Firefly-Algorithm-Inspired Framework With Band Selection and Extreme Learning Machine for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 309–320. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics; Springer: Berlin, Germany, 2001; Volume 1. [Google Scholar]
- Bau, T.C.; Sarkar, S.; Healey, G. Hyperspectral region classification using a three-dimensional Gabor filterbank. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3457–3464. [Google Scholar] [CrossRef]
- Shen, L.; Jia, S. Three-dimensional Gabor wavelets for pixel-based hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 5039–5046. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Spectral–Spatial Hyperspectral Image Classification with Edge-Preserving Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2666–2677. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Fang, L.; Benediktsson, J.A. Intrinsic Image Decomposition for Feature Extraction of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2241–2253. [Google Scholar] [CrossRef]
- 2014 IEEE GRSS Data Fusion Contest. Available online: http://www.grss-ieee.org/community/technical-committees/data-fusion/ (accessed on 25 October 2017).
- Liao, W.; Huang, X.; Coillie, F.V.; Gautama, S.; Pižurica, A.; Philips, W.; Liu, H.; Zhu, T.; Shimoni, M.; Moser, G. Processing of Multiresolution Thermal Hyperspectral and Digital Color Data: Outcome of the 2014 IEEE GRSS Data Fusion Contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2984–2996. [Google Scholar] [CrossRef]
- Sun, B.; Kang, X.; Li, S.; Benediktsson, J.A. Random-Walker-Based Collaborative Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 212–222. [Google Scholar] [CrossRef]










| Class | Samples | Methods | ||||||
|---|---|---|---|---|---|---|---|---|
| Train/Test | GE | LGE | EPF | IIDF | RCANet | HiFi | ||
| C1 | 20/26 | 99.42 ± 0.55 | 99.92 ± 0.54 | 98.84 ± 1.78 | 87.22 ± 14.9 | 99.00 ± 1.70 | 99.46 ± 1.35 | 100.0 ± 0.00 |
| C2 | 20/1408 | 70.45 ± 7.42 | 80.89 ± 5.30 | 56.53 ± 11.1 | 80.45 ± 6.04 | 63.94 ± 6.85 | 81.91 ± 5.58 | 81.88 ± 5.29 |
| C3 | 20/810 | 74.25 ± 7.71 | 85.61 ± 7.03 | 67.27 ± 10.5 | 75.89 ± 6.86 | 79.91 ± 7.05 | 91.49 ± 4.52 | 87.00 ± 5.86 |
| C4 | 20/217 | 95.10 ± 4.59 | 99.40 ± 1.14 | 96.56 ± 4.60 | 66.03 ± 10.8 | 98.59 ± 2.22 | 96.78 ± 3.84 | 99.21 ± 1.30 |
| C5 | 20/463 | 87.51 ± 5.18 | 92.13 ± 5.39 | 91.09 ± 4.56 | 93.49 ± 4.30 | 93.60 ± 3.02 | 90.06 ± 3.88 | 90.53 ± 4.21 |
| C6 | 20/710 | 92.35 ± 4.19 | 94.99 ± 3.72 | 96.97 ± 3.93 | 97.67 ± 2.11 | 98.36 ± 1.10 | 97.92 ± 1.80 | 97.21 ± 2.11 |
| C7 | 14/14 | 100.0 ± 0.00 | 100.0 ± 0.00 | 96.85 ± 3.58 | 54.08 ± 20.6 | 100.0 ± 0.00 | 96.75 ± 5.54 | 100.0 ± 0.00 |
| C8 | 20/458 | 98.56 ± 2.30 | 99.83 ± 0.52 | 96.65 ± 5.47 | 99.91 ± 0.14 | 98.76 ± 0.63 | 99.39 ± 0.92 | 99.98 ± 0.10 |
| C9 | 10/10 | 99.59 ± 0.35 | 100.0 ± 0.00 | 99.80 ± 1.41 | 44.83 ± 19.7 | 100.0 ± 0.00 | 100.0 ± 0.00 | 100.0 ± 0.00 |
| C10 | 20/952 | 73.53 ± 8.16 | 86.55 ± 5.72 | 83.09 ± 7.85 | 73.57 ± 8.49 | 87.43 ± 3.79 | 88.16 ± 6.63 | 88.97 ± 4.47 |
| C11 | 20/2435 | 69.93 ± 8.38 | 79.21 ± 5.37 | 69.55 ± 9.23 | 92.37 ± 3.52 | 72.01 ± 6.49 | 79.82 ± 5.86 | 83.97 ± 5.30 |
| C12 | 20/573 | 81.23 ± 7.01 | 85.11 ± 5.95 | 73.26 ± 10.1 | 79.13 ± 6.94 | 90.49 ± 4.08 | 93.31 ± 3.18 | 87.61 ± 5.72 |
| C13 | 20/185 | 98.76 ± 1.28 | 99.58 ± 1.16 | 99.39 ± 0.32 | 99.54 ± 1.53 | 99.49 ± 0.31 | 99.41 ± 0.29 | 99.84 ± 0.31 |
| C14 | 20/1245 | 87.16 ± 5.11 | 96.47 ± 3.63 | 88.51 ± 7.76 | 99.06 ± 1.04 | 94.24 ± 3.49 | 96.96 ± 2.79 | 96.70 ± 3.25 |
| C15 | 20/366 | 90.80 ± 6.09 | 98.21 ± 2.83 | 81.44 ± 10.6 | 84.73 ± 11.1 | 90.65 ± 4.05 | 95.23 ± 2.72 | 98.46 ± 4.23 |
| C16 | 20/73 | 98.65 ± 2.02 | 98.30 ± 2.45 | 96.93 ± 5.68 | 94.62 ± 6.86 | 99.06 ± 1.90 | 99.07 ± 0.65 | 99.75 ± 0.53 |
| OA | 79.38 ± 1.82 | 87.61 ± 1.48 | 77.54 ± 3.10 | 85.89 ± 1.88 | 83.06 ± 2.32 | 89.06 ± 1.70 | 89.55 ± 1.31 | |
| AA | 88.58 ± 1.03 | 93.51 ± 0.69 | 87.04 ± 1.88 | 82.66 ± 2.22 | 91.56 ± 0.89 | 94.11 ± 0.77 | 94.44 ± 0.73 | |
| 76.60 ± 2.03 | 85.99 ± 1.64 | 74.66 ± 3.41 | 84.02 ± 2.11 | 80.87 ± 2.56 | 87.51 ± 1.90 | 88.15 ± 1.49 | ||
| Class | Samples | Methods | ||||||
|---|---|---|---|---|---|---|---|---|
| Train/Test | GE | LGE | EPF | IIDF | RCANet | HiFi | ||
| C1 | 20/741 | 93.54 ± 2.63 | 98.84 ± 1.87 | 99.43 ± 1.13 | 99.86 ± 0.22 | 97.80 ± 1.65 | 98.60 ± 1.06 | 99.97 ± 0.11 |
| C2 | 20/223 | 68.04 ± 6.48 | 95.69 ± 5.98 | 89.65 ± 6.84 | 94.80 ± 5.55 | 95.74 ± 4.30 | 92.26 ± 5.02 | 97.04 ± 5.21 |
| C3 | 20/236 | 84.24 ± 7.53 | 99.43 ± 1.70 | 97.39 ± 1.93 | 99.42 ± 0.91 | 98.33 ± 1.39 | 96.42 ± 3.31 | 99.88 ± 0.56 |
| C4 | 20/232 | 75.14 ± 6.79 | 98.49 ± 3.04 | 93.84 ± 6.78 | 96.42 ± 3.19 | 94.17 ± 4.21 | 93.20 ± 3.50 | 97.10 ± 4.67 |
| C5 | 20/141 | 99.06 ± 1.78 | 99.91 ± 0.43 | 86.45 ± 8.63 | 97.68 ± 3.11 | 95.57 ± 5.24 | 89.78 ± 6.69 | 99.58 ± 2.90 |
| C6 | 20/209 | 93.25 ± 6.46 | 100.0 ± 0.00 | 97.96 ± 3.08 | 93.77 ± 4.61 | 94.71 ± 3.30 | 93.62 ± 7.67 | 100.0 ± 0.00 |
| C7 | 20/85 | 98.49 ± 2.77 | 100.0 ± 0.00 | 99.97 ± 0.16 | 99.93 ± 0.49 | 100.0 ± 0.00 | 95.38 ± 7.14 | 100.0 ± 0.00 |
| C8 | 20/411 | 78.00 ± 7.02 | 96.25 ± 5.49 | 98.54 ± 4.29 | 97.58 ± 4.47 | 98.27 ± 2.35 | 95.74 ± 4.47 | 96.43 ± 4.88 |
| C9 | 20/500 | 94.05 ± 5.03 | 99.28 ± 3.42 | 99.21 ± 2.49 | 99.78 ± 0.15 | 98.33 ± 4.33 | 97.58 ± 1.51 | 99.79 ± 0.73 |
| C10 | 20/384 | 91.85 ± 6.02 | 100.0 ± 0.00 | 98.81 ± 1.01 | 93.83 ± 7.04 | 98.66 ± 1.47 | 99.14 ± 1.07 | 99.79 ± 1.29 |
| C11 | 20/399 | 89.73 ± 5.27 | 100.0 ± 0.00 | 99.30 ± 1.59 | 98.60 ± 1.37 | 99.51 ± 0.83 | 97.97 ± 3.18 | 100.0 ± 0.00 |
| C12 | 20/483 | 91.61 ± 4.36 | 97.57 ± 5.27 | 96.28 ± 2.91 | 94.18 ± 4.34 | 97.97 ± 3.67 | 98.40 ± 1.46 | 99.80 ± 0.76 |
| C13 | 20/907 | 95.09 ± 3.07 | 100.0 ± 0.00 | 99.92 ± 0.15 | 99.95 ± 0.30 | 100.0 ± 0.00 | 99.71 ± 0.40 | 100.0 ± 0.00 |
| OA | 89.74 ± 1.28 | 98.91 ± 0.64 | 97.84 ± 0.90 | 97.63 ± 0.56 | 98.12 ± 0.77 | 97.09 ± 0.84 | 99.36 ± 0.54 | |
| AA | 88.62 ± 1.21 | 98.88 ± 0.65 | 96.67 ± 1.33 | 97.37 ± 0.69 | 97.62 ± 0.88 | 95.99 ± 1.19 | 99.18 ± 0.71 | |
| 88.56 ± 1.42 | 98.78 ± 0.72 | 97.58 ± 1.01 | 97.36 ± 0.62 | 97.91 ± 0.85 | 96.75 ± 0.93 | 99.28 ± 0.61 | ||
| Class | Samples | Methods | ||||||
|---|---|---|---|---|---|---|---|---|
| Train/Test | GE | LGE | EPF | IIDF | RCANet | HiFi | ||
| C1 | 20/4423 | 91.56 ± 3.65 | 96.83 ± 3.24 | 95.86 ± 4.44 | 96.39 ± 1.91 | 93.42 ± 3.03 | 96.96 ± 2.14 | 98.47 ± 0.96 |
| C2 | 20/1073 | 68.37 ± 6.93 | 41.29 ± 7.82 | 53.71 ± 17.8 | 37.33 ± 8.82 | 66.34 ± 5.88 | 64.94 ± 5.78 | 65.74 ± 12.1 |
| C3 | 20/1834 | 62.72 ± 9.78 | 53.89 ± 8.80 | 49.13 ± 17.7 | 53.38 ± 8.32 | 61.57 ± 7.37 | 68.13 ± 7.49 | 63.59 ± 7.07 |
| C4 | 20/2106 | 67.21 ± 6.62 | 61.79 ± 5.72 | 58.63 ± 18.3 | 60.91 ± 6.65 | 68.45 ± 7.39 | 62.62 ± 5.83 | 62.23 ± 10.1 |
| C5 | 20/3868 | 59.75 ± 6.53 | 73.31 ± 7.77 | 55.67 ± 16.7 | 70.54 ± 6.91 | 69.45 ± 6.38 | 76.05 ± 4.34 | 80.84 ± 3.79 |
| C6 | 20/7337 | 66.00 ± 8.46 | 92.37 ± 2.42 | 50.78 ± 13.7 | 93.37 ± 2.43 | 68.64 ± 7.35 | 67.40 ± 6.17 | 70.69 ± 8.22 |
| C7 | 20/1751 | 77.08 ± 6.94 | 81.13 ± 9.59 | 58.76 ± 12.1 | 83.01 ± 9.17 | 90.58 ± 5.31 | 84.49 ± 5.96 | 90.86 ± 4.47 |
| OA | 70.79 ± 2.47 | 76.91 ± 2.79 | 61.90 ± 6.56 | 75.37 ± 3.00 | 74.68 ± 2.69 | 75.57 ± 4.34 | 77.90 ± 2.51 | |
| AA | 70.38 ± 1.42 | 71.52 ± 2.02 | 60.36 ± 4.97 | 70.70 ± 2.55 | 74.06 ± 2.03 | 74.37 ± 6.17 | 76.06 ± 1.88 | |
| 64.69 ± 2.63 | 71.81 ± 3.17 | 54.76 ± 7.12 | 70.07 ± 3.41 | 69.15 ± 3.09 | 70.39 ± 5.95 | 73.09 ± 2.77 | ||
| Indian Pines | KSC | GRSS_DFC_2014 | |
|---|---|---|---|
| ELM | 89.55/4.07 | 99.36/1.55 | 77.90/2.64 |
| SVM | 88.98/128.3 | 99.21/45.9 | 77.75/45.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, B.; Shi, Z.; Xu, X.; Yang, Y. Hashing Based Hierarchical Feature Representation for Hyperspectral Imagery Classification. Remote Sens. 2017, 9, 1094. https://doi.org/10.3390/rs9111094
Pan B, Shi Z, Xu X, Yang Y. Hashing Based Hierarchical Feature Representation for Hyperspectral Imagery Classification. Remote Sensing. 2017; 9(11):1094. https://doi.org/10.3390/rs9111094
Chicago/Turabian StylePan, Bin, Zhenwei Shi, Xia Xu, and Yi Yang. 2017. "Hashing Based Hierarchical Feature Representation for Hyperspectral Imagery Classification" Remote Sensing 9, no. 11: 1094. https://doi.org/10.3390/rs9111094
APA StylePan, B., Shi, Z., Xu, X., & Yang, Y. (2017). Hashing Based Hierarchical Feature Representation for Hyperspectral Imagery Classification. Remote Sensing, 9(11), 1094. https://doi.org/10.3390/rs9111094