A New Low-Rank Representation Based Hyperspectral Image Denoising Method for Mineral Mapping

Abstract

Hyperspectral imaging technology has been used for geological analysis for many years wherein mineral mapping is the dominant application for hyperspectral images (HSIs). The very high spectral resolution of HSIs enables the identification and the diagnosis of different minerals with detection accuracy far beyond that offered by multispectral images. However, HSIs are inevitably corrupted by noise during acquisition and transmission processes. The presence of noise may significantly degrade the quality of the extracted mineral information. In order to improve the accuracy of mineral mapping, denoising is a crucial pre-processing task. By leveraging on low-rank and self-similarity properties of HSIs, this paper proposes a state-of-the-art HSI denoising algorithm that implements two main steps: (1) signal subspace learning via fine-tuned Robust Principle Component Analysis (RPCA); and (2) denoising the images associated with the representation coefficients, with respect to an orthogonal subspace basis, using BM3D, a self-similarity based state-of-the-art denoising algorithm. Accordingly, the proposed algorithm is named Hyperspectral Denoising via Robust principle component analysis and Self-similarity (HyDRoS), which can be considered as a supervised version of FastHyDe. The effectiveness of HyDRoS is evaluated in a series of mineral mapping experiments using noise-reduced AVIRIS and Hyperion HSIs. In these experiments, the proposed denoiser yielded systematically state-of-the-art performance.

1. Introduction

In recent years, hyperspectral imaging technology has achieved great success in many applications such as agriculture, surveillance, and mining. A convenient mental picture of a hyperspectral image (HSI) is that of a data cube formed by the collection of hundreds (even thousands) of 2D images, termed bands, representing the spectral reflectance of a given surface in contiguous spectral narrow bands. We may also interpret a HSI as the collection of spectral vectors, one per pixel, with dimension equal to the number of bands [1]. The difference between hyperspectral and multispectral images (MSIs) is application dependent, but, in general, HSIs have comparatively higher spectral and lower spatial resolution, whereas MSIs have lower spectral and higher spatial resolution [2]. In geological remote sensing, multispectral images generally offer high spatial resolution for geological mapping. The spectral resolution of these images is, however, very low, which severely constrains the application and development of mineral mapping. In order to address this problem, hyperspectral imaging provides high spectral resolution in visible, near-infrared, and shortwave infrared spectral bands. Indeed, hyperspectral imaging can be applied in many different spectral setups: Near Infrared (NIR), Mid Infrared (MIR), Raman, Terahertz (THz) spectroscopy, etc. Owing to various constraints, HSIs often cover only the visible and the infrared (IR) (in any of the modalities). The rich and detailed spectral information of HSIs opens the door to the identification and quantification of a large number of minerals with a precision beyond the reach of the techniques based on MSIs. Taking advantage of their increased information content, HSIs have been both the natural and logical choice for hyperspectral geological mapping during the last decades; a great deal of scholarly and practical attention has been devoted to the application of hyperspectral mineral mapping. Research work [3] highlights the advantages of using hyperspectral data to identify alteration minerals and defines their zonation. The work [4] uses a knowledge-based expert system to produce mineral maps from AVIRIS HSI data. Kruse et al. [5] compare Hyperion HSI data with airborne AVIRIS HSI data to show that Hyperion HSI data provides the ability to remotely map basic surface mineralogy. The relevance of having HSIs with a low level of noise or, equivalently, with a high signal-to-noise-ratio (SNR), to improve the accuracy of mineral prediction, food spectroscopy, and of various tasks such as classification and retrieving supported by spectral libraries has been pointed out, for example, in [6,7,8].

Although HSIs have become a powerful tool in regional geologic and mineral studies, there are still some obstacles, one of which is noise. For instance, EO-1 Hyperion data has been employed extensively on arid sites in Australia and South America, where it has been proven to perform really well for the location and characterization of minerals and alteration zones [5,9]. However, apart from these sites, whose area of HSIs is little affected by noise, Hyperion data has been less used, mainly because most of its images have low SNR [3]. As an important pre-processing step, denoising is necessary for nearly all subsequent processing tasks, for example, classification, unmixing, target detection, etc. It is also important in hyperspectral remote sensing geological applications, where the common processing chain is well documented and includes (1) denoising; (2) estimating the dimensionality; (3) locating the purest pixels; (3) identifying endmembers based on their spectral signatures with a spectral library or the image-derived endmembers; and (4) mapping the abundance estimation of particular endmembers. We remark that, in low SNR HSIs, the usefulness of steps (2)–(4) relies heavily on the performance of the denoising step (1) [10].

HSI denoising has attracted much research attention over the past decades due to its importance in HSIs quality improvement [11]. Initially, classical denoising algorithms conceived for 2D natural images were, with due adjustments, applied to hyperspectral data. Examples of this research line of attack are nonlocal means (NLM) [12], total variation (TV) [13], block-matching and three-dimensional collaborative filtering (BM3D) [14], and block-matching and four-dimensional collaborative filtering (BM4D) [15]. Apart from BM4D, these methods are typically applied separately in either the spatial or the spectral domain and classified as spatial-based or spectral-based HSI denoising methods.

Spatial-based or spectral-based denoising methods fail to take advantage of the high correlation between spectral and spatial dimensions, which has attracted much interest in HSI denoising research. Recently, many spectral–spatial based denoising methods have been developed. In [16], a principal component analysis (PCA) combined to BM4D method is proposed for HSI denoising. Firstly, the principal component scores are filtered by PCA, and then, the low score components are filtered by BM4D. Lately, low-rank property of HSI has been widely exploited and low-rank based frameworks have become increasingly popular for HSI denoising [17]. Low-rank matrix recovery (LRMR) in [18] is implemented with ssGoDec for HSI noise removal and achieves noticeable denoising results. Meanwhile, in order to extend the LRMR framework in the hyperspectral denoising problem, a noise-adjusted iterative low-rank matrix approximation (NAILRMA) [19] method has been proposed by considering the fact that the noise intensity varies from hyperspectral bands, which is more realistic than the previous work [18], namely closer to real scenarios. The recently introduced FastHyDe [20] denoising algorithm fully exploits the low-rank and self-similarity properties of HSIs. FastHyDe starts by estimating the subspace where the spectral vectors live, herein termed the signal subspace, and then denoises the representation coefficient images, herein termed eigen-images using a state-of-the-art self-similarity denoiser. Experimental results in [20] have shown that FastHyDe is state-of-the-art and, arguably, the fastest HSI denoising algorithm.

Contribution

HyDRoS, the denoising algorithm herein proposed, is inspired by FastHyDe. As in FastHyDe, HyDRoS exploits HSI low-rank property and self-similarity by implementing two consecutive steps: (1) signal subspace learning; and (2) denoising the eigen-images associated with the representation coefficients using a self-similarity based state-of-the-art denoising algorithm. Since the signal subspace has much smaller dimension than the number of bands, the first step largely attenuates the noise and renders a much lighter inverse problem, from the computational point of view. The second step exploits the fact that the eigen-images are self-similar, and thus they may be effectively denoised with a state-of-the-art self-similarity based denoiser.

The main contributions regard a robust estimation of the signal subspace and the assessment of HSI denoising performance in mineral mapping applications. In more detail, the contributions are the following:

• Decomposing the observed data as the sum of a low-rank matrix and a sparse matrix containing outliers. The decomposition is solved by the robust principle component analysis (RPCA) algorithm [21]. The estimated signal subspace corresponds to the column span of the low-rank matrix and is a sub-product of RPCA. This procedure, which allows to control the dimension of the signal subspace by a proper setting of the RPCA regularization parameters, brings robustness to the signal subspace estimation and underlies performance gains with respect to an unsupervised version of FastHyDe, as shown in Section 3.
• Extending the application of HSI denoising methods. The denoised spectra are used to do hyperspectral mineral mapping by two methods: Spectral Angle Mapping (SAM) [22] and Spectral Feature Fitting (SFF) [23]. Using the noise-reduced HSI data, pixels related to three kinds of minerals presented in the Cuprite data sets, NV, USA, namely Alunite, Chalcedony, and Kaolinite, are mapped by SAM and SFF methods. Receiver operating characteristic (ROC) curves [24] and the area under ROC curves (AUC) are displayed to evaluate the mapping accuracy, which can be considered as an indicator of the denoising performance.

The rest of this paper is organized as follows: Section 2 introduces the low-rank representation based HyDRoS denoising method. Section 3 evaluates the performance of the proposed method by comparison with state-of-the-art HSI denoising methods in both simulated data with artificial noise and real data experiments using the data sets collected by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) and Hyperion on board NASA’s EO-1 satellite over the Cuprite Mining District, NV, USA. Then, hyperspectral mineral mapping is conducted on the noise-reduced HSI data sets obtained by different denoising methods to show the impact of denoising on mineral mapping accuracy. Section 4 discusses the denoising performance for the proposed HyDRoS algorithm. Finally, Section 5 presents conclusions and remarks.

2. Proposed Low-Rank Representation Based Denoising Method

High dimensional hyperspectral data admits low-rank and sparse representations owing to the very high correlation among spectral channels and spatial pixels [25,26]. For the hyperspectral remote sensing image denoising problem, the low-rank representation (LRR) based method has proven to be a powerful tool [19,20,27,28]. The proposed hyperspectral denoising method integrates spatial filtering, in addition to a low-rank structure, which promotes self-similar bands. Section 2.1 explains the low-rank structure of HSI in detail; Section 2.2 introduces eigen-image filtering, exploiting self-similarity; Section 2.3 proposes our denoising method combining low-rank representation and eigen-image filtering.

2.1. Low-Rank Structure Of HSI

Let $\mathbf{X}=\left[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_n\right]\in {\mathbf{R}}^{n_b\times n}$ be a matrix representation of a given HSI with n spatial samples (the columns of $\mathbf{X}$) of size $n_b$ (the number of bands). In the hyperspectral imaging systems carried on satellite platforms, there is often the problem that some pixels are much noisier than others and sparsely distributed (relative to the independent identically distributed (i.i.d) noise) [29]. These perturbations are called outliers and are represented by matrix $\mathbf{S}\in {\mathbf{R}}^{n_b\times n}$. The degradation model of the observed HSI, which is denoted by $\mathbf{Y}=\left[{\mathbf{y}}_1,\dots ,{\mathbf{y}}_n\right]\in {\mathbf{R}}^{n_b\times n}$, is often expressed as the sum of a noise-free HSI matrix $\mathbf{X}$, an outlier matrix $\mathbf{S}$, and additive noise $\mathbf{N}\in {\mathbf{R}}^{n_b\times n}$, that is,

$$\mathbf{Y}=\mathbf{X}+\mathbf{S}+\mathbf{N}.$$

(1)

In real-world HSIs, the high correlation among bands implies that the rank of $\mathbf{X}$ is much lower than $n_b$ [28]. Therefore, $\mathbf{X}$ in Equation (1) can be expressed by a linear combination of a basis $\mathbf{E}=\left[{\mathrm{e}}_1,\dots ,{\mathrm{e}}_p\right]\in {\mathbf{R}}^{n_b\times p}$ and a coefficient matrix $\mathbf{Z}=\left[{\mathrm{z}}_1,\dots ,{\mathrm{z}}_n\right]\in {\mathbf{R}}^{p\times n}$ with respect to (w.r.t) $\mathbf{E}$, with $p\ll n_b$:

$$\mathbf{X}=\mathbf{EZ}.$$

(2)

Figure 1 illustrates a common property of HSIs: the dimension of signal subspace, p, is much lower than the number of bands, $n_b$. Figure 1 is given as an example in real scenarios: Figure 1a,b show a clean data cube $\mathbf{X}\in {\mathbf{R}}^{n_b\times n}$ and a noisy HSI data cube $\mathbf{Y}\in {\mathbf{R}}^{n_b\times n}$, respectively. Figure 1c plots the eigenvalues of the sample correlation matrices $\mathbf{X}{\mathbf{X}}^T/n$ and $\mathbf{Y}{\mathbf{Y}}^T/n$ ordered by non-increasing values. Clearly, the bulk of the signal energy, shown in green, is able to be explained by less than $p=6$ components; while the bulk of noisy observation energy, shown in red, can only be explained by using a number of components much higher than p due to the existence of noise.

We herein adopt RPCA, firstly proposed by Wright et al. [21], to estimate the p-dimensional signal subspace from the noisy observation $\mathbf{Y}$, with $p\ll n_b$. RPCA decomposes the observed data matrix $\mathbf{Y}\in {\mathbf{R}}^{m\times n}$ into the sum of a low-rank matrix $\mathbf{X}\in {\mathbf{R}}^{m\times n}$ and a sparse matrix $\mathbf{S}\in {\mathbf{R}}^{m\times n}$.

The RPCA problem in the presence of noise can be formulated as

$$\underset{\mathbf{X},\mathbf{S}}{min}\frac{1}{2}\parallel \mathbf{Y}-\mathbf{X}-\mathbf{S}{\parallel }_F^2+\tau \mathrm{rank}\left(\mathbf{X}\right)+\gamma {\parallel \mathbf{S}\parallel }_0,$$

(3)

where ${\parallel \mathbf{X}\parallel }_F^2=\mathrm{trace}\left({\mathbf{XX}}^T\right)$ is the Frobenious norm of $\mathbf{X}$, ${\left|\right|\mathbf{S}\left|\right|}_0$ denotes the number of non-zero components of $\mathbf{S}$, abusively termed the ${\ell }_0$-norm of $\mathbf{S}$, and $\tau , \gamma > 0$ set the relative weight of the terms rank(X) and ${\left|\right|\mathbf{S}\left|\right|}_0$. Optimization Equation (3) is non-convex and no efficient solution is known. Following a popular approach [30,31,32], in order to obtain a tractable optimization problem, we replace the $l_0$-norm with $l_1$-norm given by ${\left|\right|\mathbf{S}\left|\right|}_1={\sum }_{i=1}^n{\parallel {\mathbf{s}}_i\parallel }_1$, where ${\mathbf{s}}_i$ denotes the i-th columns of $\mathbf{S}$, and rank(X) with the nuclear norm $\left|\right|\mathbf{X}|{|}_{*}={\sum }_i{\sigma }_i\left(\mathbf{X}\right)$ , where ${\sigma }_i\left(\mathbf{X}\right)$ denotes the i-th singular value of $\mathbf{X}$. The obtained convex optimization is written as

$$\underset{\mathbf{X},\mathbf{S}}{min}\frac{1}{2}\parallel \mathbf{Y}-\mathbf{X}-\mathbf{S}{\parallel }_F^2+{\tau \parallel \mathbf{X}\parallel }_{*}+\gamma {\parallel \mathbf{S}\parallel }_1,$$

(4)

where $\tau ,\lambda > 0$ set the relative weight of the terms $\left|\right|\mathbf{X}|{|}_{*}$ and $\left|\right|\mathbf{S}|{|}_1$ and are manually adjusted.

Considering that RPCA is a robust subspace learning method against sparse outliers, we employ RPCA to estimate the signal subspace $\mathbf{E}$ and outliers matrix $\mathbf{S}$ from noisy HSI observation. To solve optimization Equation (4), and under the assumption on i.i.d noise, we run the publicly available accelerated proximal gradient singular value thresholding algorithm [33], which terminates in $O\left(1/\sqrt{ϵ}\right)$ iterations with an $ϵ$-optimal solution. Part of the computational effectiveness of this algorithm relies on the use of the PROPACK package [34] to efficiently compute partial singular value decompositions (SVDs).

2.2. Eigen-Image Filtering Exploiting Self-Similarity

From the estimated outlier matrix $\tilde{\mathbf{S}}$, we compute

$$\tilde{\mathbf{Y}}:=\mathbf{Y}-\tilde{\mathbf{S}}.$$

(5)

Then, the observation model of $\tilde{\mathbf{Y}}$ becomes

$$\tilde{\mathbf{Y}}=\mathbf{X}+\mathbf{N}=\mathbf{EZ}+\mathbf{N},$$

(6)

where matrix $\mathbf{E}=[{\mathbf{e}}_1,\cdots ,{\mathbf{e}}_p]\in {\mathbb{R}}^{n_b\times p}$ is obtained by solving Equation (4). As already mentioned, the p rows of $\mathbf{Z}$ are termed eigen-images. We remark that

$$\mathbf{X}=\mathbf{EZ}=\sum _{i=1}^p{\mathbf{e}}_i\mathbf{Z}(i,:),$$

(7)

where $\mathbf{Z}(i,:)$ denotes the i-th eigen-image, that is, the i-th row of $\mathbf{Z}$. Given the observation model Equation (6), our denoising inverse problem consists in computing $\widehat{\mathbf{X}}=\mathbf{E}\widehat{\mathbf{Z}},$ where $\widehat{\mathbf{X}}$ and $\widehat{\mathbf{Z}}$ are estimates of $\mathbf{X}$ and of $\mathbf{Z}$, respectively. At this point, a few remarks are worth noting:

• Let ${\mathbf{P}}_E$ and ${\mathbf{P}}_E^{\perp }$ denote, respectively, the projection matrices onto $\mathrm{span}\left(\mathbf{E}\right)$, that is, onto the linear space spanned by the columns of $\mathbf{E}$ and onto the orthogonal complement of $\mathrm{span}\left(\mathbf{E}\right)$. Multiplying ${\mathbf{P}}_E$ by $\tilde{\mathbf{Y}}$, we have ${\mathbf{P}}_E\tilde{\mathbf{Y}}=\mathbf{EZ}+{\mathbf{P}}_E\mathbf{N}$ and ${\mathbf{P}}_E^{\perp }\tilde{\mathbf{Y}}={\mathbf{P}}_E^{\perp }\mathbf{N}$. We conclude, therefore, that $\mathbf{Z}$ is affected only by ${\mathbf{P}}_E\mathbf{N}$ which, in the case of i.i.d. noise, has power $p/n_b$ times smaller than power of $\mathbf{N}$. The representation in the subspace alone yields therefore a large noise attenuation.
• From the equation $\mathbf{Z}={\left({\mathbf{E}}^T\mathbf{E}\right)}^{-1}{\mathbf{E}}^T\mathbf{X}$, we conclude that the eigen-images are linear combinations of the bands of $\mathbf{X}$. Since the hyperspectral bands represent reflectance of the same surface at different wavelengths, the spatial structure of the self-similarity is the same across all HSI bands. We conclude, therefore, that the eigen-images are self-similar as well.

In order to clarify the two above remarks clearly, Figure 2 shows the eigen-images obtained by projecting an HSI into the low dimensional signal subspace. Figure 2a–c are 2nd–4th eigen-images $\widehat{\mathbf{Z}}={\mathbf{P}}_E\tilde{\mathbf{Y}}$ of the AVIRIS HSI data set acquired at Cuprite, NV, USA, and it is clear that there is still some residual noise in the eigen-images. A natural conclusion is that the eigen-images $\widehat{\mathbf{Z}}={\mathbf{P}}_E\tilde{\mathbf{Y}}$ may be effectively denoised by a state-of-the-art self-similarity based algorithm. In this work, we use BM3D [14], which operates on a single image. BM3D is based on an enhanced sparse representation in the transform domain and is realized by three successive steps for groups of similar patches: 3-D transformation, collaborative filtering, and inverse 3-D transformation. Figure 2d–f show the BM3D filtered eigen-images corresponding to Figure 2a–c, in which the noise is obviously reduced. Figure 2 shows that BM3D efficiently filters out the noise from the eigen-images.

2.3. Proposed HyDRoS Algorithm

The inverse problem which consists in estimating $\mathbf{Z}$ from $\tilde{\mathbf{Y}}$ is formalized as follows:

$$\begin{array}{cc}\hfill \widehat{\mathbf{Z}}& =arg\underset{\mathbf{Z}}{min}\frac{1}{2}\left|\right|\mathbf{EZ}-\tilde{\mathbf{Y}}{\left|\right|}_F^2+\lambda \varphi \left(\mathbf{Z}\right)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & =arg\underset{\mathbf{Z}}{min}\frac{1}{2}\left|\right|\mathbf{Z}-{\mathbf{E}}^T\tilde{\mathbf{Y}}{\left|\right|}_F^2+\lambda \varphi \left(\mathbf{Z}\right),\hfill \end{array}$$

(9)

The first term on the right hand side of Equation (8) is the data fidelity; $\varphi \left(\mathbf{Z}\right)$ is a regularizer tailored to promote self-similar images, and $\lambda > 0$ is a regularization parameter. The optimization Equation (9) follows from Equation (8) because matrix $\mathbf{E}$ is, by design, orthogonal, that is, ${\mathbf{E}}^T\mathbf{E}={\mathbf{I}}_p$, where ${\mathbf{I}}_p$ stands for the identity matrix of size p.

Owing to the orthogonality of $\mathbf{E}$, the components of $\mathbf{Z}$ tend to be decorrelated. Although decorrelation does not imply independency, it is a necessary condition. Herein, we assume that function $\varphi$ is decoupled w.r.t. the eigen-images. Therefore, the solution of optimization Equation (9) is to decouple each row of $\mathbf{Z}$; this may be written as

$$\widehat{\mathbf{Z}}={\phi }_{\lambda \varphi }\left({\mathbf{E}}^T\tilde{\mathbf{Y}}\right)=\left[\begin{array}{c}{\phi }_{\lambda {\varphi }_1}\left({\mathbf{e}}_1^T\tilde{\mathbf{Y}}\right)\\ ⋮\\ {\phi }_{\lambda {\varphi }_p}\left({\mathbf{e}}_p^T\tilde{\mathbf{Y}}\right)\end{array}\right],$$

(10)

where ${\phi }_{\lambda {\varphi }_i}\left(\mathbf{y}\right)=arg\underset{\mathbf{w}}{min}\frac{1}{2}\left|\right|\mathbf{y}-\mathbf{w}{\left|\right|}_F^2+\lambda {\varphi }_i\left(\mathbf{w}\right)$, for $i=1,\dots ,p$, is the so-called proximity operator of ${\varphi }_i$ [35]. In this paper, we apply BM3D as a denoiser for each eigen-image. That is, instead of investing efforts in tailoring regularizer ${\varphi }_i$, promoting self-similar images and then computing its proximity operators, we directly use a state-of-the-art denoiser conceived to enforce self-similarity. We selected BM3D, as it is the state-of-the-art, very fast to implement and is publicly available. The denoised HSI is estimated as

$$\widehat{\mathbf{X}}=\mathbf{E}\widehat{\mathbf{Z}}.$$

(11)

Algorithm 1 shows the pseudo code of the proposed algorithm.

Algorithm 1 HyDRoS denoising algorithm

1: Input: Noisy HSI observation $\mathbf{Y}$ 2: Learn subspaces basis $\mathbf{E}\in {\mathbf{R}}^{n_b\times p}$ and outliers matrix S from $\mathbf{Y}$ by RPCA 3: Compute $\tilde{\mathbf{Y}}:=\mathbf{Y}-\tilde{\mathbf{S}}$ 4: Filter the eigen-images: $\widehat{\mathbf{Z}}={\phi }_{\lambda \varphi }\left({\mathbf{E}}^T\tilde{\mathbf{Y}}\right)$ by BM3D 5: Compute the inverse transform $\widehat{\mathbf{X}}=\mathbf{E}\widehat{\mathbf{Z}}$ to obtain the noise reduced HSI 6: Output: Denoised HSI $\widehat{\mathbf{X}}$

3. Experiments and Results

The proposed denoising algorithm HyDRoS is tested with simulated and real data. Hyperspectral data sets collected by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) and NASA’s EO-1 Hyperion sensor at Cuprite, NV, USA, are used as simulated data and real data, respectively. In the simulated data experiments, artificial noise is added to high SNR AVIRIS data to get the simulated noisy AVIRIS HSIs. The denoising performance is evaluated by comparing the noise-reduced HSI data with original AVIRIS data. In the real data experiments, the comparatively low SNR Hyperion HSI data is directly used as real data without a clean reference.

To further verify the effectiveness of the proposed HyDRoS with both high SNR and low SNR HSI data sets, hyperspectral mineral mapping experiments at Cuprite, NV, USA, are conducted on the noise-reduced HSI data sets. Cuprite, NV, USA, located approximately 200 km northwest of Las Vegas, is well understood mineralogically [5,36,37] and has been used as a geological remote sensing test site since the early 1980s [36,38,39,40,41]. Among the 18 minerals presented in this area, three of them (Alunite, Chalcedony, and Kaolinite) are selected because their outcrops can be spatially and spectrally clearly identified with both high SNR AVIRIS and low SNR Hyperion HSI data simultaneously. In hyperspectral geological mapping and exploration, minerals can be more accurately identified with high SNR HSI data [4]. Therefore, the mapping accuracy of the three minerals provides evidence of the quality of the noise-reduced HSI data, and can be considered as an indicator of denoising performance.

Six state-of-the-art HSI denoising methods are used as comparative methods in both simulated and real experiments, namely BM3D [14], BM4D [15], PCA + BM4D [16], LRMR [27], NAILRMA [19] and FastHyDe [20]. BM3D, a single band filter, is applied to HSI band by band. PCA + BM4D first performs PCA to the noisy HSI data cube and uses a BM4D filter to reduce the noise in the low score components. LRMR is a HSI restoration method based on low-rank matrix recovery, and NAILRMA is a patch-wise low-rank matrix approximation based HSI denoising method under an iterative regularization framework. The parameters in LRMR and NAILRMA are manually tuned to obtain optimal results in our experiment. FastHyDe is an efficient fast hyperspectral denoising method based on low-rank and sparse representations. Note that, we implemented an unsupervised version of FastHyDe, wherein called FastHyDe(un), where the subspace is learnt by HySime [42], which is an unsupervised estimation technique conceived to preserve the signal subspace directions with SNR>1.

3.1. Simulated Data Experiments with AVIRIS HSI Data

3.1.1. Data Description

In the simulated data experiments, the AVIRIS HSI data set is used as simulated data with added artificial noise. The data was captured at Cuprite, NV, USA, by AVIRIS hyperspectral sensor on 2 May 2006. AVIRIS hyperspectral sensor collects data in 224 contiguous spectral bands with a bandwidth of 10 nm, and has a contiguous spectrum over the range from 400 nm to 2500 nm. The spatial resolution of AVIRIS HSI data used in this study is 3.4 m.

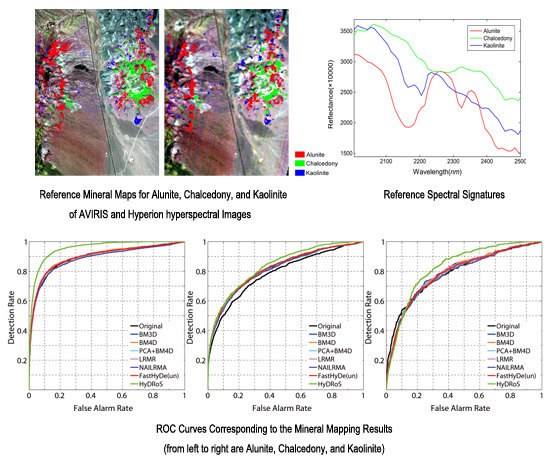
Figure 3a shows a false-color composite image of AVIRIS HSI data captured at Cuprite Mining District; Figure 3b,c are a reference mineral map and reference spectral signatures of the three dominant minerals. This data set can be retrieved from http://aviris.jpl.nasa.gov/. Spectral bands covering between 2000 nm and 2400 nm in shortwave infrared (SWIR) wavelength range are particularly useful for mineralogical mapping studies because SWIR contains a large number of absorption features which may be used as a diagnostic of the presence of certain hydroxyl and carbonate bearing minerals or mineral groups [43]. In this study, 51 AVIRIS hyperspectral bands (band 174–224 or wavelength range from 2004.8 nm to 2503.5 nm) of size 2100 rows × 1560 columns, have been selected in the experiments with simulated data.

3.1.2. Evaluation Indexes

In simulated data, the evaluation of the proposed denoising HyDRoS algorithm is carried out by quantitative assessment of the noise-reduced image quality and mineral mapping accuracy.

Two full reference indexes are used for noise-reduced image quality evaluation: the peak signal-to-noise ratio (PSNR) and the structural similarity (SSIM). Artificial noise is added to the high SNR AVIRIS data to get the simulated noisy AVIRIS HSIs, while the original AVIRIS data is regarded as a clean reference. MPSNR and MSSIM denote the mean PSNR and mean SSIM index over bands. Note that SSIM in this paper refers to the structural similarity index metric of one band, and MSSIM refers to the mean value of the SSIM index over all bands, which are different from the definitions of SSIM and MSSIM in [44]. Both indexes are full reference metrics that require a reference image and a denoised image. Higher index values indicate better image quality.

Mineral mapping accuracy is used as a quality indicator for noise-reduced HSI data sets. SAM [22] and SFF [23] are implemented to identify the three dominant minerals at Cuprite Mining District. SAM is used for the similarity measurement between the unknown mineral spectra and the reference spectra. SFF is an absorption feature based methodology utilized to fit the unknown spectra to the reference spectra. It compares the fit of unknown spectra to reference spectra using a least-squares technique.

Mineral mapping accuracy estimated by SAM and SFF is presented in the form of receiver operating characteristics (ROC) [24] curves and the area under ROC curves (AUC). ROC curves provide visual information about the performance of binary mineral mapping using the noise-reduced HSI data. The horizontal coordinate of the ROC curve indicates the false alarm rate, while the vertical coordinate indicates the detection rate. AUC is estimated to compare the overall mapping accuracies for different denoising methods.

3.1.3. Experimental Results

In the simulated data experiments, Gaussian i.i.d. noise and non-i.i.d. noise is added to AVIRIS hyperspectral data (of size 2100 rows × 1560 columns × 51 bands). AVIRIS data is used as a reference in denoising because the spectral bands of AVIRIS have high SNR [45]. As one of the bands (2493.6 nm) in the SWIR spectral range is heavily contaminated by noise, it was removed and 50 bands are ultimately selected. The gray values of each HSI band are normalized to [0, 1] before denoising and converted to the original level after that. Since the additive noise model is the situation usually found in HSIs and many HSI denoising algorithms have been derived based on this model [46], Gaussian i.i.d. noise is added to the reference AVIRIS data in case 1; the variance values are 0.02, 0.04, 0.06, 0.08 and 0.1. However, in real scenarios, the simplified assumption of i.i.d. noise breaks down, and the noise which exists in a natural HSI is usually non-i.i.d, namely with band-dependent variance [11]. In other words, different bands in HSI have different noise variances. So different variance zero-mean Gaussian noise is added to each band of the reference AVIRIS data in case 2, and the variance values are randomly selected from 0 to 0.1 with the mean value of 0.053. Noise variance in each case is presented in Figure 4.

The HSI noise degradation model Equation (1) assumes Gaussian i.i.d. noise, meaning that $\mathbf{N}$ is constituted by additive, zero-mean, Gaussian noise. If the spectral vectors ${\mathbf{n}}_i$ in $\mathbf{N}$ are uncorrelated, then the covariance matrix ${\mathbf{C}}_{\lambda }=E\left[{\mathbf{n}}_i{\mathbf{n}}_i^T\right]$ is diagonal and ${\mathbf{C}}_{\lambda }={\sigma }^2\mathbf{I}$. This is not the case with non-i.i.d noise, where the spectral vectors are correlated, thus the covariance is not a diagonal matrix. In order to convert the non-i.i.d noise to i.i.d noise, a whitening transformation [47,48] is applied to the observation $\tilde{\mathbf{Y}}$ prior to the denoising methods in case 2. Let

$$\widehat{\mathbf{Y}}:=\sqrt{{\mathbf{C}}_{\lambda }^{-1}}\tilde{\mathbf{Y}},$$

(12)

where ${\mathbf{C}}_{\lambda }$ is the covariance matrix of $\tilde{\mathbf{Y}}$. The whitened data $\widehat{\mathbf{Y}}$ is uncorrelated and has unit variance. In practice, a small constant $\epsilon ={10}^{-4}$ is added to ${\mathbf{C}}_{\lambda }$ to prevent singularities. The noise degradation model in case 2 becomes

$$\widehat{\mathbf{Y}}=\sqrt{{\mathbf{C}}_{\lambda }^{-1}}\mathbf{X}+\sqrt{{\mathbf{C}}_{\lambda }^{-1}}\mathbf{N}.$$

(13)

Subsequently, the proposed HyDRoS denoising model can be formulated as

$$\widehat{\tilde{\mathbf{Z}}}=arg\underset{\mathbf{Z}}{min}\frac{1}{2}\left|\right|\tilde{\mathbf{Z}}-{\tilde{\mathbf{E}}}^T\widehat{\mathbf{Y}}{\left|\right|}_F^2+\lambda \varphi \left(\tilde{\mathbf{Z}}\right).$$

(14)

Finally, the noise-reduced HSI can be estimated as

$$\widehat{\tilde{\mathbf{X}}}=\mathbf{E}\widehat{\tilde{\mathbf{Z}}},$$

(15)

$$\widehat{\mathbf{X}}=\sqrt{{\mathbf{C}}_{\lambda }}\widehat{\tilde{\mathbf{X}}}.$$

(16)

Table 1. Quantitative assessment of the different denoising algorithms applied to AVIRIS hyperspectral data at Cuprite Mining District.

	$\mathit{\sigma }$	Index	Noisy Image	BM3D	BM4D	PCA+BM4D	LRMR	NAILRMA	FastHyDe	HyDRoS
Case 1	0.02	MPSNR (dB)	33.98	39.16	43.52	45.38	44.16	46.11	45.61	47.23
		MSSIM	0.7899	0.9268	0.9715	0.9813	0.9756	0.9832	0.9865	0.9870
	0.04	MPSNR (dB)	27.96	37.23	40.12	40.27	40.96	42.20	43.27	44.03
		MSSIM	0.5049	0.9030	0.9432	0.9474	0.9655	0.9636	0.9752	0.9757
	0.06	MPSNR (dB)	24.44	35.21	38.38	37.59	38.83	39.67	41.30	42.04
		MSSIM	0.3294	0.8564	0.9213	0.9007	0.9392	0.9377	0.9631	0.9637
	0.08	MPSNR (dB)	21.94	34.33	37.23	35.22	36.94	37.66	40.26	40.70
		MSSIM	0.2285	0.8379	0.9030	0.8439	0.9022	0.9043	0.9521	0.9523
	0.1	MPSNR (dB)	20.00	33.69	36.37	33.42	35.66	36.01	39.22	39.68
		MSSIM	0.1676	0.8256	0.8861	0.7839	0.8683	0.8662	0.9420	0.9418
Case 2		MPSNR (dB)	27.51	32.94	38.02	36.78	38.57	42.43	43.99	44.93
		MSSIM	0.4619	0.8048	0.9066	0.8806	0.9350	0.9670	0.9837	0.9838

shows MPSNR and MSSIM indexes of the noise-reduced AVIRIS HSI data, in which the highest values are shown in bold and where HyDRoS achieves the highest values in almost every case.

Figure 5 presents the PSNR value of each band in detail for the noise-reduced AVIRIS HSI data obtained by the seven denoising methods in case 1 and case 2. HyDRoS displays significantly higher values than competitors in both cases.

Figure 6 shows that the hyperspectral signal can be completely restored using a subspace of very low dimension, and the highest PSNR value for the dimension of the subspace it chooses.

Figure 7 compares the spectral signatures of the three minerals denoised by HyDRoS with the reference spectral signatures. Figure 7a is the spectrum signatures of Alunite; Figure 7b is the spectrum signatures of Chalcedony; Figure 7c is the spectrum signatures of Kaolinite. Since case 2 is closer to real scenario, the denoised spectral signatures in Figure 7 are selected from noise-reduced data in case 2.

Figure 8 and Figure 9 compare ROC curves of mineral mapping results obtained by SAM and SFF methods using noise-reduced AVIRIS HSI data, in which the curve closer to the upper left corner reveals higher mineral mapping accuracy.

Table 2. AUC obtained by SAM for AVIRIS noise-reduced HSI data at Cuprite Mining District.

	Alunite	Chalcedony	Kaolinite
Noisy	0.7508	0.6878	0.7396
BM3D	0.9880	0.9693	0.9679
BM4D	0.9913	0.9358	0.9842
PCA + BM4D	0.9746	0.8671	0.9351
LRMR	0.9697	0.9168	0.8981
NAILRMA	0.9903	0.9756	0.9815
FastHyDe(un)	0.9936	0.9139	0.9836
HyDRoS	0.9941	0.9808	0.9888

and

Table 3. AUC obtained by SFF for AVIRIS noise-reduced HSI data at Cuprite Mining District.

	Alunite	Chalcedony	Kaolinite
Noisy	0.7886	0.4884	0.6269
BM3D	0.9825	0.6620	0.8598
BM4D	0.9800	0.6178	0.8743
PCA + BM4D	0.8936	0.5448	0.7860
LRMR	0.9615	0.5703	0.7951
NAILRMA	0.9807	0.5872	0.8744
FastHyDe(un)	0.9861	0.5183	0.8924
HyDRoS	0.9877	0.6508	0.8948

present AUC values of ROC curves in Figure 8 and Figure 9, in which the highest values are shown in bold and HyDRoS gets the highest value for every mineral.

3.2. Real Data Experiments With Hyperion HSI Data

3.2.1. Data Description

The Hyperion HSI data set is used as real data. The data was captured at Cuprite, NV, USA, by Hyperion hyperspectral sensor on 19 September 2011. Hyperion hyperspectral sensor collects data in 242 channels with a spectral resolution of 10 nm, and has a contiguous spectrum covering from 355.0 nm to 2577.0 nm. The spatial resolution of Hyperion HSI data used in this study is approximately 30 m.

Figure 10a shows a false-color composite image of Hyperion HSI data captured at Cuprite Mining District; Figure 10b,c are a reference mineral map and reference spectral signatures of the three minerals. The data set used in this study is Hyperion level 1R data and can be retrieved from https://earthexplorer.usgs.gov/. Level 1R data has already been radiometrically corrected, but it still needs the following pre-processing before conducting mineral mapping: band selection, destriping, atmospheric correction, geometric correction and registration. The flowchart of pre-processing steps is shown in Figure 11. Forty out of the Hyperion hyperspectral bands (band 185–224 or wavelength range from 2002.1 nm to 2395.5 nm) of size 238 rows × 176 columns are selected for mineral mapping in the real data experiment.

3.2.2. Evaluation Indexes

The evaluation of the proposed denoising HyDRoS algorithm is performed by visual comparison, quantitative assessment with mineral mapping accuracy, and computational time.

Since the reference is unknown, we resort to visual evaluation to get a qualitative assessment of the noise-reduced Hyperion HSI data.

Mineral mapping accuracy is used as a quantitative assessment for the denoising performance of HyDRoS, which is the same evaluation as in the simulated data experiments. ROC curves and AUC obtained by SAM and SFF methods are used to illustrate the validity of the HyDRoS denoising algorithm.

Computation time of different denoising methods is compared to evaluate the computational performance of HyDRoS in the real data experiment.

3.2.3. Experimental Results

Figure 12 presents the denoising results of the 37-th band (2365.2 nm) for Hyperion HSI data, in which Figure 12h denoised by HyDRoS shows the best visual quality.

Figure 13 and Figure 14 compare ROC curves of mineral mapping results obtained by SAM and SFF methods using noise-reduced Hyperion HSI data, in which the curve closer to the upper left corner reveals higher mineral mapping accuracy.

Table 4. AUC obtained by SAM for Hyperion noise-reduced HSI data at Cuprite Mining District.

	Alunite	Chalcedony	Kaolinite
Original	0.8925	0.7852	0.8278
BM3D	0.8972	0.8152	0.7935
BM4D	0.8984	0.8190	0.7929
PCA + BM4D	0.8856	0.8098	0.7823
LRMR	0.8965	0.8094	0.7910
NAILRMA	0.8837	0.8094	0.7799
FastHyDe(un)	0.8952	0.8181	0.7870
HyDRoS	0.9547	0.8350	0.8278

and

Table 5. AUC obtained by SFF for Hyperion noise-reduced HSI data at Cuprite Mining District.

	Alunite	Chalcedony	Kaolinite
Original	0.8077	0.4443	0.6311
BM3D	0.8337	0.4369	0.6383
BM4D	0.8315	0.4302	0.6353
PCA + BM4D	0.8227	0.4306	0.6305
LRMR	0.8205	0.4149	0.6257
NAILRMA	0.8178	0.4305	0.6233
FastHyDe(un)	0.8314	0.4345	0.6519
HyDRoS	0.8983	0.5062	0.6983

present AUC values of ROC curves in Figure 13 and Figure 14, in which the highest values are shown in bold and HyDRoS obtains the highest value in every mineral.

Computational time is presented in the caption of Figure 12 and the shortest time is shown in bold. The algorithms were implemented using MATLAB R2014a on a desktop PC equipped with eight Intel Core i7-6700 CPU @ 3.4 GHz and 8 GB of RAM memory.

4. Discussion

This section discusses the denoising performance of HyDRoS and the results are shown in Section 3.1.3 and Section 3.2.3. Before the discussion, we remark that all the compared methods, apart from FastHyDe(un), are supervised in the sense that the parameters are tuned for optimal performance. FastHyDe(un), on the contrary, is unsupervised and therefore cannot be considered as a direct competitor.

Based on the performance evaluation in the simulated data experimental results from Section 3.1.3, it can be seen in Table 1 and Figure 5 that HyDRoS gets the highest PSNR and SSIM index values in almost every case. In case 1, as the noise variance level increases from 0.02 to 0.1 in Figure 5a–e, the PSNR value decreases gradually, in which HyDRoS almost manages to get the highest PSNR value in every band and every case. In case 2 of Table 1, which is closer to real scenario, HyDRoS gets the highest PSNR and SSIM index values. Quantitative assessment of the noise-reduced HSI data with PSNR and SSIM indexes shows that HyDRoS is effective with respect to HSI image quality improvement. The denoised spectral signatures of case 2 in Figure 7 show good agreement with the reference spectral signatures, which provides evidence that HyDRoS can efficiently recover the spectral signatures as well, though they are heavily contaminated by noise. Figure 6 gives evidence that the robust subspace identification used in HyDRoS contributes to its performance gains. ROC curves in Figure 8 and Figure 9 compare the mineral mapping accuracy of the seven denoising methods, in which HyDRoS gets almost uniformly the highest accuracy for every mineral. Table 2 and Table 3 present the corresponding AUC values of Figure 8 and Figure 9, in which higher AUC indicates better image quality and HyDRoS manages to achieve the best performance. Figure 8 and Figure 9 and Table 2 and Table 3 reveal that HyDRoS significantly improves mineral mapping accuracy compared with competitors, indicating its effectiveness for HSI denoising. In terms of image quality and mineral mapping accuracy evaluations, HyDRoS achieves the best denoising performance in the simulated data experiments.

Based on the performance evaluation in real data experimental results from Section 3.2.3, it can be seen that HyDRoS achieves a good visual effect in Figure 12. ROC curves in Figure 13 and Figure 14 show that HyDRoS significantly improves mineral mapping accuracy when compared with the original noisy HSI data, and achieves higher accuracy than other denoising methods. AUC values corresponding to Figure 13 and Figure 14 in Table 4 and Table 5 illustrate that the highest mineral mapping accuracy is implemented with HyDRoS. Regarding the computational time shown in the caption of Figure 12, HyDRoS is within an acceptable range, relative to the competitors such as BM4D, PCA + BM4D and NAILRMA. In terms of visual effect, computational time and mineral mapping accuracy evaluations, HyDRoS outperforms other HSI denoising methods in the real data experiment.

5. Conclusions

Hyperspectral image denoising is an important pre-processing step for subsequent applications. The proposed HSI low-rank representation based denoising method, called HyDRoS, implements three steps: firstly, it applies RPCA to get the signal subspace and eigen-images of the observed HSI under the low-rank constraint, then it applies a BM3D filter to denoise the eigen-images, exploiting the self-similarity property, and finally the noise-reduced HSI is obtained by an inverse transformation. The structure of HyDRoS parallels the structure of FastHyDe(un). The main difference is that the former uses RPCA, with a mild form of supervision, to estimate the signal subspace and the presence of outliers, whereas the latter does not consider outliers and learns the subspace blindly. This difference turns out to be important and is the main reason for the better performance of HyDRoS.

This study highlights the importance of denoising for hyperspectral mineral mapping. Two hyperspectral data sets acquired at Cuprite, NV, USA, were used as simulated and real data, respectively. Both simulated and real data experiments provide evidence that noise-reduced AVIRIS and Hyperion hyperspectral data helps to improve the mineral mapping accuracy with SAM and SFF methods, and that the proposed HyDRoS markedly outperforms the state-of-the-art denoising methods. Compared to FastHyDe(un), the proposed denoiser is slower owing to the process of outliers removal by RPCA. Removal of the outliers will be subjected to future research aiming at improvements in regard to computational time. In addition, this study focuses on three dominant minerals at the Cuprite Mining District. More applications using HyDRoS could be carried out in the future, using HSIs acquired with various sensors, using all the available wavelengths range and/or focusing on other minerals.