Statistical Modeling of Polarimetric SAR Data: A Survey and Challenges
Abstract
:1. Introduction
2. Polarimetric SAR
3. Gaussian Statistics
3.1. Gaussian Distribution
3.2. Wishart Distribution
3.2.1. Relaxed Wishart Model
3.2.2. Wishart-Kotz Distribution
4. Texture Model
4.1. Scalar Texture Model
4.1.1. Distribution
4.1.2. Normal Inverse Gaussian (NIG)
4.1.3. and Distributions
4.1.4. Kummer- Distribution
4.1.5. Distribution
4.1.6. Distribution
4.1.7. Wishart-Generalized Gamma Distribution
4.1.8. Generalized Distribution
4.2. Multi-Texture Model
4.2.1. Correlated Distribution
4.2.2. Dual-Texture Distribution
5. Other Models
5.1. Finite Mixture Model
5.2. Copula Based Model
- , the copula is equal to 0 if at least one parameter is 0.
- , the copula is equal to if all parameters are 1 except .
- For each hyperrectangle where , the C-volume of B is non-negativewhere represents the corners of the hyperrectangle, and is the number of elements in reaching the lower bound of the hyperrectangle.
6. Model Analysis
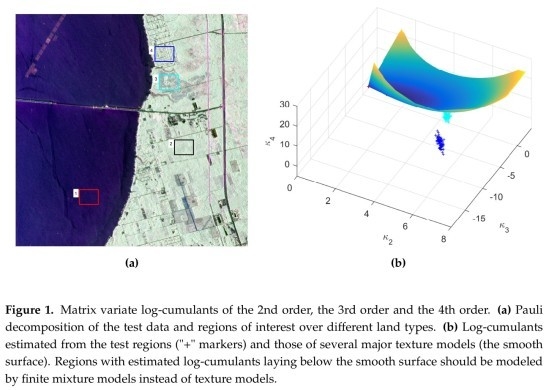
7. Challenges
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BSA | Back Scattering Alignment |
| CDF | Cumulative Distribution Function |
| CLT | Central Limit Theorem |
| FSA | Forward Scattering Alignment |
| GIG | Generalized Inverse Gaussian |
| NIG | Normal Inverse Gaussian |
| NIM | Normalized Intensity Gaussian |
| Probability Density Function | |
| PolSAR | Polarimetric SAR |
| ROI | Region Of Interest |
| SAR | Synthetic Aperture Radar |
| SIRV | Spherically Invariant Random Vector |
Appendix A
- ([74] p. 340, Equation (3.339))is the modified Bessel function of the first kind.
- ([74] p. 702, Equation (6.624-1))
- ([74] p. 347, Equation (3.382-2))
- ([74] p. 700, Equation (6.621-3))is the Gauss hypergeometric function.
- ([74] p. 917, Equation (8.432-3))
- ([74] p. 325, Equation (3.252-3))
- The gamma function is defined asLet where , we have the following equation after changing variables
- ([34] p. 505, Equation (13.2.5))U is the confluent hypergeometric function of the second kind, or KummerU function.
- ([74] p. 368, Equation (3.471-5))M is the confluent hypergeometric function of the first kind, also known as the KummerM function.
References
- Goodman, J.W. Some fundamental properties of speckle. JOSA 1976, 66, 1145–1150. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; De Grandi, G. Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar]
- Kersten, P.R.; Lee, J.S.; Ainsworth, T.L. Unsupervised classification of polarimetric synthetic aperture radar images using fuzzy clustering and EM clustering. IEEE Trans. Geosci. Remote Sens. 2005, 43, 519–527. [Google Scholar] [CrossRef]
- Doulgeris, A.P.; Anfinsen, S.N.; Eltoft, T. Classification with a non-Gaussian model for PolSAR data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2999–3009. [Google Scholar] [CrossRef]
- Bombrun, L.; Vasile, G.; Gay, M.; Totir, F. Hierarchical segmentation of polarimetric SAR images using heterogeneous clutter models. IEEE Trans. Geosci. Remote Sens. 2011, 49, 726–737. [Google Scholar] [CrossRef]
- Doulgeris, A.P.; Akbari, V.; Eltoft, T. Automatic PolSAR segmentation with the U-distribution and Markov random fields. In Proceedings of the 2012 EUSAR—9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012; pp. 183–186. [Google Scholar]
- Lee, J.S.; Mitchell, R.G.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution. Int. J. Remote Sens. 1994, 15, 2299–2311. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.; Ainsworth, T.; Du, L.J.; Schuler, D.; Cloude, S. Unsupervised classification using polarimetric decomposition and the complex Wishart classifier. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2249–2258. [Google Scholar]
- Jakeman, E.; Pusey, P.N. A model for non-Rayleigh sea echo. IEEE Trans. Antennas Propag. 1976, 24, 806–814. [Google Scholar] [CrossRef]
- Jakeman, E.; Pusey, P. Significance of K distributions in scattering experiments. Phys. Rev. Lett. 1978, 40, 546–550. [Google Scholar] [CrossRef]
- Ward, K. Compound representation of high resolution sea clutter. Electron. Lett. 1981, 17, 561–563. [Google Scholar] [CrossRef]
- Yueh, S.H.; Kong, J.A.; Jao, J.K.; Shin, R.T.; Novak, L.M. K-distribution and polarimetric terrain radar clutter. J. Electromagn. Waves Appl. 1989, 3, 747–768. [Google Scholar] [CrossRef]
- Lee, J.S.; Schuler, D.L.; Lang, R.H.; Ranson, K.J. K-distribution for multi-look processed polarimetric SAR imagery. In Proceedings of the International Geoscience and Remote Sensing Symposium, Surface and Atmospheric Remote Sensing: Technologies, Data Analysis and Interpretation, Pasadena, CA, USA, 8–12 August 1994; Volume 4, pp. 2179–2181. [Google Scholar]
- Frery, A.C.; Muller, H.J.; Yanasse, C.C.F.; Sant’Anna, S.J.S. A model for extremely heterogeneous clutter. IEEE Trans. Geosci. Remote Sens. 1997, 35, 648–659. [Google Scholar] [CrossRef]
- Freitas, C.C.; Frery, A.C.; Correia, A.H. The polarimetric G distribution for SAR data analysis. Environmetrics 2005, 16, 13–31. [Google Scholar] [CrossRef]
- Bombrun, L.; Beaulieu, J.M. Fisher distribution for texture modeling of polarimetric SAR data. IEEE Geosci. Remote Sens. Lett. 2008, 5, 512–516. [Google Scholar] [CrossRef]
- Moser, G.; Zerubia, J.; Serpico, S.B. Dictionary-based stochastic expectation-maximization for SAR amplitude probability density function estimation. IEEE Trans. Geosci. Remote Sens. 2006, 44, 188–200. [Google Scholar] [CrossRef]
- Krylov, V.; Moser, G.; Serpico, S.B.; Zerubia, J. Modeling the Statistics of High Resolution SAR Images; Technical Report; Institut National de Recherche en Informatique et en Automatique, INRIA: Rocquencourt, France, 2008. [Google Scholar]
- Wang, Y.; Ainsworth, T.L.; Lee, J. On Characterizing High-Resolution SAR Imagery Using Kernel-Based Mixture Speckle Models. IEEE Geosci. Remote Sens. Lett. 2015, 12, 968–972. [Google Scholar] [CrossRef]
- Gao, G. Statistical modeling of SAR images: A survey. Sensors 2010, 10, 775–795. [Google Scholar] [CrossRef] [PubMed]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Mercier, G.; Bouchemakh, L.; Smara, Y. The use of multidimensional copulas to describe amplitude distribution of polarimetric SAR data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 2236–2239. [Google Scholar]
- Voisin, A.; Krylov, V.A.; Moser, G.; Serpico, S.B.; Zerubia, J. Supervised Classification of Multisensor and Multiresolution Remote Sensing Images With a Hierarchical Copula-Based Approach. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3346–3358. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Cloude, S. Polarisation: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A Model for Radar Images and Its Application to Adaptive Digital Filtering of Multiplicative Noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, PAMI-4, 157–166. [Google Scholar] [CrossRef]
- Kong, J.; Yueh, S.; Lim, H.; Shin, R.; Van Zyl, J. Classification of earth terrain using polarimetric synthetic aperture radar images. Prog. Electromagn. Res. 1990, 3, 327–370. [Google Scholar]
- Sarabandi, K. Derivation of phase statistics from the Mueller matrix. Radio Sci. 1992, 27, 553. [Google Scholar] [CrossRef]
- Ulaby, F.; Sarabandi, K.; Nashashibi, A. Statistical properties of the Mueller matrix of distributed targets. In Proceedings of the IEE Proceedings F—Radar and Signal Processing, Barcelona, Spain, 6 August 1992; Volume 139, pp. 136–146. [Google Scholar]
- Goodman, N.R. Statistical analysis based on a certain multivariate complex Gaussian distribution (An Introduction). Ann. Math. Stat. 1963, 34, 152–177. [Google Scholar] [CrossRef]
- Lee, J.S.; Hoppel, K.W.; Mango, S.A.; Miller, A.R. Intensity and phase statistics of multilook polarimetric and interferometric SAR imagery. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1017–1028. [Google Scholar]
- Tough, R.J.A.; Blacknell, D.; Quegan, S. A statistical description of polarimetric and interferometric synthetic aperture radar data. Proc. R. Soc. Lond. A Math. Phys. Sci. 1995, 449, 567–589. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Courier Corporation: North Chelmsford, MA, USA, 1964; Volume 55. [Google Scholar]
- Walck, C. Hand-Book on Statistical Distributions for Experimentalists; University of Stockholm: Stockholm, Sweden, 2007. [Google Scholar]
- López-Martínez, C.; Fabregas, X. Polarimetric SAR speckle noise model. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2232–2242. [Google Scholar] [CrossRef]
- López-Martínez, C.; Pottier, E.; Cloude, S.R. Statistical assessment of eigenvector-based target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2058–2074. [Google Scholar] [CrossRef]
- Alonso-González, A.; López-Martínez, C.; Salembier, P. Filtering and segmentation of polarimetric SAR data based on binary partition trees. IEEE Trans. Geosci. Remote Sens. 2012, 50, 593–605. [Google Scholar] [CrossRef]
- Anfinsen, S.N.; Eltoft, T.; Doulgeris, A.P. A relaxed Wishart model for polarimetric SAR data. In Proceedings of the Fourth International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry PoIInSAR; European Space Agency: Noordwijk, The Netherlands, 2009; pp. 26–30. [Google Scholar]
- Kersten, P.R.; Anfinsen, S.N. A flexible and computationally efficient density model for the multilook polarimetric covariance matrix. In Proceedings of the 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012; pp. 760–763. [Google Scholar]
- Kersten, P.R.; Anfinsen, S.N.; Doulgeris, A.P. The Wishart-Kotz classifier for multilook polarimetric SAR data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3146–3149. [Google Scholar]
- Anfinsen, S.N.; Eltoft, T. Application of the matrix-variate Mellin transform to analysis of polarimetric radar images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2281–2295. [Google Scholar] [CrossRef]
- Novak, L.M.; Burl, M.C. Optimal speckle reduction in polarimetric SAR imagery. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 293–305. [Google Scholar] [CrossRef]
- Sheen, D.R.; Johnston, L.P. Statistical and spatial properties of forest clutter measured with polarimetric synthetic aperture radar (SAR). IEEE Trans. Geosci. Remote Sens. 1992, 30, 578–588. [Google Scholar] [CrossRef]
- Gini, F.; Greco, M. Covariance matrix estimation for CFAR detection in correlated heavy tailed clutter. Signal Process. 2002, 82, 1847–1859. [Google Scholar] [CrossRef]
- Pascal, F.; Forster, P.; Ovarlez, J.; Larzabal, P. Performance analysis of covariance matrix estimates in impulsive noise. IEEE Trans. Signal Process. 2008, 56, 2206–2217. [Google Scholar] [CrossRef]
- Vasile, G.; Ovarlez, J.P.; Pascal, F.; Tison, C. Coherency matrix estimation of heterogeneous clutter in high-resolution polarimetric SAR images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1809–1826. [Google Scholar] [CrossRef]
- Bombrun, L.; Anfinsen, S.N.; Harant, O. A complete coverage of log-cumulant space in terms of distributions for Polarimetric SAR data. In Proceedings of the 5th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry (POLinSAR 2011), Friscati, Italy, 24–28 January 2011; pp. 1–8. [Google Scholar]
- Doulgeris, A.; Anfinsen, S.N.; Eltoft, T. Analysis of non-Gaussian POLSAR data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposiumm, Barcelona, Spain, 23–28 July 2007; pp. 160–163. [Google Scholar]
- Doulgeris, A.P.; Eltoft, T. Scale Mixture of Gaussian Modelling of Polarimetric SAR Data. EURASIP J. Adv. Signal Process. 2009, 2010, 874592. [Google Scholar]
- Koudou, A.E.; Ley, C. Characterizations of GIG laws: A survey. Probab. Surv. 2014, 11, 161–176. [Google Scholar] [CrossRef]
- Khan, S.; Guida, R. Application of Mellin-Kind Statistics to Polarimetric G Distribution for SAR Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3513–3528. [Google Scholar] [CrossRef]
- Tison, C.; Nicolas, J.M.; Tupin, F.; Maître, H. A new statistical model for Markovian classification of urban areas in high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2046–2057. [Google Scholar] [CrossRef]
- Song, W.; Li, M.; Zhang, P.; Wu, Y.; Jia, L.; An, L. The WGΓ Distribution for Multilook Polarimetric SAR Data and Its Application. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2056–2060. [Google Scholar] [CrossRef]
- Bian, Y.; Mercer, B. Multilook polarimetric SAR data probability density function estimation using a generalized form of multivariate K-distribution. Remote Sens. Lett. 2014, 5, 682–691. [Google Scholar] [CrossRef]
- De Grandi, G.; Lee, J.S.; Schuler, D.; Nezry, E. Texture and speckle statistics in polarimetric SAR synthesized images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2070–2088. [Google Scholar] [CrossRef]
- Eltoft, T.; Anfinsen, S.N.; Doulgeris, A.P. A multitexture model for multilook polarimetric radar data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1048–1051. [Google Scholar]
- Yu, Y. Textural-partially correlated polarimetric K-distribution. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Seattle, WA, USA, 6–10 July 1998; Volume 1, pp. 60–62. [Google Scholar]
- Eltoft, T.; Anfinsen, S.N.; Doulgeris, A.P. A multitexture model for multilook polarimetric synthetic aperture radar data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2910–2919. [Google Scholar] [CrossRef]
- Doulgeris, A.P.; Anfinsen, S.N.; Eltoft, T. Segmentation of polarimetric SAR data with a multi-texture product model. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Nuremberg, Germany, 22–27 July 2012; pp. 1437–1440. [Google Scholar]
- Lombardo, P.; Farina, A. Coherent radar detection against K-distributed clutter with partially correlated texture. Signal Process. 1996, 48, 1–15. [Google Scholar] [CrossRef]
- Khan, S.; Guida, R. The new dual-texutre G distribution for single-look PolSAR data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Nuremberg, Germany, 22–27 July 2012; pp. 1469–1472. [Google Scholar]
- Anfinsen, S.N. Statistical Unmixing of SAR Images; Technical Report; Munin Open Research Archive, University of Tromsø—The Arctic University of Norway: Tromsø, Norway, 2016. [Google Scholar]
- Wang, Y.; Ainsworth, T.L.; Lee, J.S. Application of Mixture Regression for Improved Polarimetric SAR Speckle Filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 453–467. [Google Scholar] [CrossRef]
- Frühwirth-Schnatter, S. Finite Mixture and Markov Switching Models; Springer: Berlin, Germany, 2006. [Google Scholar]
- McNeil, A.J.; Frey, R.; Embrechts, P. Quantitative Risk Management: Concepts, Techniques and Tools; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Mercier, G.; Moser, G.; Serpico, S.B. Conditional copulas for change detection in heterogeneous remote sensing images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1428–1441. [Google Scholar] [CrossRef]
- Regniers, O.; Bombrun, L.; Guyon, D.; Samalens, J.C.; Germain, C. Wavelet-based texture features for the classification of age classes in a maritime pine forest. IEEE Geosci. Remote Sens. Lett. 2015, 12, 621–625. [Google Scholar] [CrossRef]
- Oliver, C. Fundamental properties of high-resolution sideways-looking radar. IEEE F-Commun. Radar Sig. 1982, 129, 385–402. [Google Scholar] [CrossRef]
- Deng, X.; López-Martínez, C. Higher Order Statistics for Texture Analysis and Physical Interpretation of Polarimetric SAR Data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 912–916. [Google Scholar] [CrossRef]
- Nicolas, J.M. Introduction aux statistiques de deuxième espèce: Applications des logs-moments et des logs-cumulants à l’analyse des lois d’images radar. TS. Traitement du Signal 2002, 19, 139–167. [Google Scholar]
- Deng, X.; López-Martínez, C.; Varona, E.M. A Physical Analysis of Polarimetric SAR Data Statistical Models. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3035–3048. [Google Scholar] [CrossRef]
- Deng, X.; López-Martínez, C. On the Use of the l2-Norm for Texture Analysis of Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6385–6398. [Google Scholar] [CrossRef]
- Jeffrey, A.; Zwillinger, D. Table of Integrals, Series, and Products, 7th ed.; Academic Press: Boston, MA, USA, 2007. [Google Scholar]







| Category | Model | References | Summary | |
|---|---|---|---|---|
| Gaussian | Gaussian | (7) | [31,33] | Simple, high mathematical tractability, suitable for data of low or moderate spatial resolution. |
| Wishart | (21) | [31,32,33] | ||
| Relaxed Wishart | (21) | [39] | More flexible than the Wishart distribution, but assigning different values to the number of looks L is not so convincing. | |
| Wishart-Kotz | (31) | [40,41] | With ability to model heavy tail behaviors, computationally efficient and numerically stable, but at the expense of adding two more parameters. | |
| Texture Models | (43), (44) | [4,7,10] | Suitable for non-Gaussian data, widely used to model forest, ocean and so on, strong physical background. | |
| NIG | (47), (48) | [49,50] | Large shape variations, strong theoretical grounds derived from Brownian motion. | |
| (52), (53) | [14,15,52] | Able to model different types of texture, but requires more parameters (two parameters). | ||
| (57), (58) | [14,15] | Suitable for extremely heterogeneous data, no complex special function involved. | ||
| Kummer- | (62), (63) | [16,53] | Able to model different types of texture, but requires more parameters (two parameters), texture distribution belongs to Pearson family. | |
| (67), (68) | [5] | Able to model data with low variance but extreme skewness, e.g., textured data after speckle filtering. | ||
| (72), (73) | [5] | |||
| WG | No Explicit | [54] | Of great flexibility (generalization of many other distributions), but the PDF needs to be calculated numerically. | |
| Generalized | (81) | [55] | Good approximation of data when there exist strong scatterers, very complex PDF with polynomial expansions. | |
| Correlated | No Explicit | [58,61] | Able to model texture correlations of different channels, no explicit expression for the texture variables, distribution parameters are limited to specific values. | |
| Dual-Texture | (92) | [62] | Different texture distributions for the co-pol and the cross-pol channels. | |
| Others | Finite Mixture | (93) | [17,18,19] | Extremely flexible (covering both unimodal and multimodal distributions), able to model data with considerable skewness, suitable for rather heterogeneous data. |
| Copula Based | No Explicit | [22,67] | Divides complex multivariate distributions into marginal distributions and dependence structure, and analyze them separately, but it is not very straightforward to choose the best copulas. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, X.; López-Martínez, C.; Chen, J.; Han, P. Statistical Modeling of Polarimetric SAR Data: A Survey and Challenges. Remote Sens. 2017, 9, 348. https://doi.org/10.3390/rs9040348
Deng X, López-Martínez C, Chen J, Han P. Statistical Modeling of Polarimetric SAR Data: A Survey and Challenges. Remote Sensing. 2017; 9(4):348. https://doi.org/10.3390/rs9040348
Chicago/Turabian StyleDeng, Xinping, Carlos López-Martínez, Jinsong Chen, and Pengpeng Han. 2017. "Statistical Modeling of Polarimetric SAR Data: A Survey and Challenges" Remote Sensing 9, no. 4: 348. https://doi.org/10.3390/rs9040348
APA StyleDeng, X., López-Martínez, C., Chen, J., & Han, P. (2017). Statistical Modeling of Polarimetric SAR Data: A Survey and Challenges. Remote Sensing, 9(4), 348. https://doi.org/10.3390/rs9040348