Signal Processing for a Multiple-Input, Multiple-Output (MIMO) Video Synthetic Aperture Radar (SAR) with Beat Frequency Division Frequency-Modulated Continuous Wave (FMCW)

Abstract

In this paper, we present a novel signal processing method for video synthetic aperture radar (ViSAR) systems, which are suitable for operation in unmanned aerial vehicle (UAV) environments. The technique improves aspects of the system’s performance, such as the frame rate and image size of the synthetic aperture radar (SAR) video. The new ViSAR system is based on a frequency-modulated continuous wave (FMCW) SAR structure that is combined with multiple-input multiple-output (MIMO) technology, and multi-channel azimuth processing techniques. FMCW technology is advantageous for use in low cost, small size, and lightweight systems, like small UAVs. MIMO technology is utilized for increasing the equivalent number of receiving channels in the azimuthal direction, and reducing aperture size. This effective increase is achieved using a co-array concept by means of beat frequency division (BFD) FMCW. A multi-channel azimuth processing technique is used for improving the frame rate and image size of SAR video, by suppressing the azimuth ambiguities in the receiving channels. This paper also provides analyses of the frame rate and image size of SAR video of ViSAR systems. The performance of the proposed system is evaluated using an exemplary system. The results of analyses are presented, and their validity is verified using numerical simulations.

1. Introduction

Synthetic aperture radar (SAR) technology is an active microwave remote sensing technique, capable of day/night, all-weather operation, used to detect and acquire electromagnetic information about objects without physical contact [1,2,3]. The enormous potential of SAR—invented by Carl Wiley in 1951—has been evident since the first demonstration of the concept. This potential has facilitated extensive research into SAR technology [4], including avenues for improving its operation. For instance, in the case of conventional single aperture SAR, it is difficult to obtain a high-resolution wide swath image, due to the trade-off between resolution and image size [5]. This problem was solved by adopting multi-channel processing techniques to create a high-resolution wide swath (HRWS) SAR system [6,7,8,9,10]. By adding multiple transmit antennas to the HRWS SAR system using multiple-input multiple-output (MIMO) technology, it is possible to operate a single SAR system in multiple modes, such as HRWS, interferometric SAR (InSAR), and polarimetric SAR (PolSAR). These modes can be operated simultaneously, without performance degradation [11,12]. By applying MIMO and multi-channel azimuth processing techniques to video synthetic aperture radar (ViSAR), improvements to the frame rate and image size of SAR video can be achieved, without compromising other aspects of the system’s performance.

ViSAR is a SAR imaging mode which has recently gained increased research interest. In this mode, images can be generated at a much higher rate than in conventional SAR; thus, they can be viewed continuously, just like watching a video [13,14,15]. Since ViSAR systems can provide high resolution SAR images at a high frame rate regardless of adverse weather conditions, they can be utilized in many day/night, all-weather military and civilian applications, including fire control support [16], as a replacement for electro-optical (EO)/infrared (IR) sensors, which can be only operated in clear weather, land and maritime traffic monitoring, and surveillance [17].

There are two kinds of SAR video synthesis methods associated with ViSAR, full aperture synthesis, which uses a circular SAR mode [13,15], and sub-aperture synthesis, which uses a spotlight SAR mode [14,16]. In the full aperture synthesis mode, an overlapped processing method is typically used between SAR video frame updates to obtain high frame rates, since the synthetic aperture time is very long at relatively low frequencies. Due to its parallel nature and ease of motion compensation, the backprojection algorithm (BPA) is suitable for use with full aperture synthesis. The frame rate in this case can be adjusted easily by changing the overlapping ratio between SAR video frames. Due to the large amount of computation power required, the BPA uses sub-images generated from sub-apertures, which are partial sections of the full aperture. In the sub-aperture synthesis mode, the frame rate can be improved by increasing the transmitted frequency and the radar velocity at a given resolution. When operated as a partial measurement, circular SAR is the same as spotlight SAR. Therefore, on a circular path, SAR video can be generated from the sub-aperture data, using the polar format algorithm (PFA) in spotlight SAR mode. However, as the radar velocity increases, the Doppler bandwidth of the antenna beamwidth increases, thus, azimuth ambiguities occur. These azimuth ambiguities can be suppressed effectively, using multi-channel azimuth processing techniques.

The X band video SAR system (XWEAR) [13], generates SAR video using the BPA on a circular path. The NanoSAR, operating in the X band, and the MiniSAR, operating in the Ku band, can also perform the video SAR function using a circular path. The Defense Advanced Research Projects Agency (DARPA) is currently developing a ViSAR system capable of achieving a high frame rate at an extremely high frequency (233 GHz), to replace EO/IR sensors used for fire control on maneuvering ground targets [15,16]. The Agency for Defense Development (ADD)—a defense research center in the Republic of Korea—is currently in the process of developing a 94-GHz airborne MIMO video SAR system, as a possible concept for surveillance sensors in unmanned aerial vehicles (UAVs).

Frequency-modulated continuous wave (FMCW) technology is suitable for small size, lightweight and low cost systems. Various technologies and algorithms related to FMCW-based SAR systems have been studied in [11,18,19]. Several FMCW SAR systems have historically been used successfully in ice measurement, environment monitoring, and three-dimensional applications [20]. The combination of FMCW technology and ViSAR mode gives birth to a light-weight, cost-effective, high-resolution, active microwave remote sensing instrument, which is suitable for small platforms such as UAVs [20].

In 1994, Paulraj and Kailath patented the use of multiple antennas for both transmission and reception in wireless communications, in order to increase channel capacity [21]. This invention has shown important potential for deployment in various wireless communication applications, as well as for radar sensor technology. The potential applications of this technology have promoted extensive research on the use of multiple antennas. The MIMO radar, the combination of multiple antennas with radar sensors, is currently one of the most interesting topics in radar communities [22]. In this case, the MIMO function is implemented using a coding technique to apply a pseudo-orthogonal waveform. This solution is not suitable for SAR operation, because, unlike the point target case, the received signal consists of distributed targets from large swaths, in the time-frequency domain [23]. Orthogonal frequency division multiplexing (OFDM) chirp [24,25], short-term shift orthogonal (STSO) waveforms [26], and OFDM chirp diverse waveforms [27] have been studied with pulsed MIMO SAR.

MIMO technology can be combined with ViSAR systems using orthogonal waveforms for FMCW radars such as the beat frequency division (BFD) waveform [28], the chirp rate division waveform [28], and the OFDM (or interleaved OFDM, I-OFDM) chirp waveform [29]. This MIMO technology can be used for various objectives, for example, the virtual array can be used to increase the equivalent number of phase centers or receiving channels, for the reduction of the aperture size. When reconfigurable transmitting (Tx) antennas are employed, MIMO technology can also be used for multi-mode operation within a single system [12,25], such as along-track interferometry, ground moving target indication (GMTI), and polarimetric SAR. In this paper, we use MIMO technology to increase the equivalent number of receive channels of a virtual array, and to reduce aperture size, by combining it with a ViSAR system. The stop-and-go approximation used in pulsed SAR is not valid for FMCW SAR. Since an FMCW SAR has a long sweep duration, the motion of the target object within the sweep must be considered [11]. Doppler shift is more sensitive in OFDM chirp waveforms [24,25], than in linear frequency modulation (LFM) [29]. It is therefore difficult to apply Doppler compensation techniques when the sweep duration is long, as in FMCW SAR. This problem can be solved by applying the BFD FMCW, and then compensating the Doppler shift. As such, the proposed MIMO ViSAR system is based on this orthogonal FMCW.

A multi-channel azimuth processing technique is utilized for improving the frame rate and image size of SAR video by suppressing the azimuth ambiguities in the receiving channels. Applying the multi-channel reconstruction algorithm (MCRA) to the ViSAR system allows SAR image formation without Doppler ambiguities, which are due to the simultaneous increase of the Doppler bandwidth and the radar velocity [6,7,8,9]. As a result, the frame rate and image size of the SAR video can be increased. There exist several different HRWS algorithms and MCRAs for reconstructing a stationary scene. These include the matrix inversion method [6,7,8,9], the orthogonal projection method [9], the maximum signal method [9], the maximum signal-to-ambiguity-plus-noise ratio (SANR) method [9], the minimum mean-square error (MMSE) method [30], and the improved digital beamforming (IDBF) method [10]. In addition, in [17], the GMTI function is implemented by extending the MCRA to the case of imaging moving targets. A method for simultaneously imaging moving and stationary targets is presented in [31]. This paper focuses on the imaging of stationary targets.

When ViSAR is operated on a circular path, the azimuth and the elevation beamwidth are selected to be of similar magnitudes for efficient observation of targets [23]. In this case, the beamwidths can be widened, depending on the requirements of the specific scenario. In the case of a wide beam, it is difficult to apply the PFA, due to the scene size limitation associated with this algorithm. The BPA is advantageous for generating SAR image frames at high frame rates in an overlapping fashion due to its parallel nature. Therefore, the BPA is often applied to ViSAR. However, this algorithm is not suitable for synthesizing SAR images in real time, on small platforms such as UAV, due to its huge computational burden and large memory usage. Conversely, the PFA can be applied when using a narrow beam. In this case, a SAR video can be generated by continuously forming the SAR images from a sub-aperture that is a part of the full circular aperture that has been selected to satisfy the scene size limitation of the PFA.

The PFA, which was developed by Walker [32], is the classical algorithm proposed for raw data processing of spotlight SAR [2]. Although the PFA is significantly faster than the BPA, it approximates a matched filter response, thereby causing image errors in large scenes. Due to these errors, the PFA has a scene size limitation. Since the PFA can be implemented easily for a circular and a linear path, it is possible to operate the SAR system more flexibly. Therefore, video from the proposed MIMO ViSAR system is formed using the PFA.

In this paper, we derive a signal model based on the MIMO radar signal model, and propose a novel signal processing method for ViSAR systems suitable for UAV environment operation, which improves aspects of the system performance, such as frame rate, and image size of the SAR video. The proposed ViSAR system focuses on a sub-aperture synthesis method. The new ViSAR system is based on a FMCW SAR structure that is combined with MIMO and multi-channel azimuth processing techniques, to make use of the characteristics listed above. MIMO technology is utilized for increasing the equivalent number of receiving channels in the azimuthal direction, and reducing the aperture size using a co-array concept with a BFD FMCW. A multi-channel azimuth processing technique is utilized for improving the frame rate and image size of the SAR video, by suppressing the azimuth ambiguities in the receiving channels. This paper also provides analyses of the frame rate and image size of SAR video. The performance of the proposed system is evaluated using an exemplary system comprised of two Tx and two receiving (Rx) channels. The results of analyses are presented, and their validity is verified using numerical simulations.

This paper consists of five sections and is organized as follows. We start with an overview of ViSAR systems and analysis of the frame rate and image size in Section 2. In Section 3, we describe the MIMO signal model and MIMO video SAR processing steps. In Section 4, an exemplary system is designed and the numerical simulation results and performance estimation are given. Finally, conclusions and future opportunities are presented in Section 5.

2. Theory of Video SAR

To gain a better understanding of its operation, the basic concept, the frame rate, and the image size of the ViSAR system are described in detail in this section.

2.1. Overview

ViSAR is a SAR imaging technique in which the radar is operated in spotlight mode on a circular flight path, as shown in Figure 1. Radar data is collected on a region of interest, and images are generated at high frame rates. The ViSAR system can generate electromagnetic SAR images at frame rates similar to conventional video formats, which are typically 2 ∼ 5 Hz or more.

Figure 1 shows the ViSAR geometry when it is operated on a circular path. There are two kinds of image formation methods used in ViSAR with circular antenna motion: full synthetic aperture methods [13,15] and sub-aperture methods [14,16]. As the name suggests, in the full synthetic aperture method, SAR images are generated from the full aperture, which corresponds to the complete circular path. In this case, an ultimate resolution of $\frac{\lambda }{4}$ can be obtained. Another advantage of this method is that images are acquired over 360 degrees. If a full aperture image is synthesized every time data is obtained, the frame rate becomes very small. Also, as the BPA is typically used in forming a full aperture image, the computation power required is very large. Therefore, a fast-factorized BPA is used in order to increase the frame rate and reduce the computation load, by factorizing the full synthetic aperture into sub-apertures, and updating the SAR image every time sub-aperture data is obtained. A higher frame rate can be obtained because the SAR image is updated in a sliding window fashion; the update is performed every time sub-aperture data is modified instead of waiting for a full aperture data update. Conventional ViSAR systems often use this method [13]. Since fast-factorized BPA updates the image using the sliding window method, it has the disadvantage that an afterimage is retained in the SAR image. This is also seen with circular SAR when there is a large amount of overlap between input data. The fast-factorized BPA can achieve a high frame rate, even at relatively low frequencies [15,16].

The sub-aperture method for circular antenna motion is a method for synthesizing SAR images that uses only data obtained from the sub-aperture, which is a fraction of the full aperture. This is the same as operation in spotlight SAR mode, with partial measurement of a circular path. In this case, it is possible to update the SAR image at a high frame rate without an afterimage. However, since the SAR image must be synthesized using only sub-aperture data, the synthetic aperture time must be short to achieve a high frame rate. Therefore, at a given resolution, the transmitted frequency or the speed of the radar should be high. In addition, as only sub-aperture data is used, this technique is less restricted by the flight path than the full aperture method. Therefore, it is suitable for applications such as weapon assignment [15,16]. In this paper, we will focus mainly on the sub-aperture method.

When ViSAR is operated in spotlight SAR mode on a circular path, the direction of the image changes according to the aspect angle of the SAR image. Because of this, stationary targets appear to rotate in the SAR video. In this case, it would be convenient to interpret the SAR images as if they were taken from an optical camera at a fixed point. To do this, a reference angle is defined. SAR images obtained at different aspect angles are subsequently rotated and aligned to this reference. This reference angle is called the cardinal direction up (CDU), as shown in Figure 2. ${\theta }_{as}$ denotes the aspect angle with respect to the cardinal direction.

2.2. Frame Rate

The frame rate is one of the most important parameters in the ViSAR system. In ViSAR, the frame rate is proportional to the inverse of the SAR video frame time, which is a fraction of the synthetic aperture time (SAT) and therefore can be expressed as:

$$f_v=\frac{1}{T_f}$$

(1)

where $T_f$ is the SAR video frame time, which is defined as:

$$T_f=F_o{T}_a$$

(2)

where $T_a$ is the SAT and $F_o$ is the overlap ratio between SAR video frames. Note that $F_o$ = 1 describes the non-overlap processing condition, which will be applied throughout this paper.

For spotlight SAR mode (or partial measurement of circular SAR) on a circular path, the synthetic aperture time for spotlight SAR can be expressed as [2] Equation (2.21)):

$$T_a=\frac{L}{v}=\frac{\lambda R_a{K}_a}{v·2{\rho }_a\sin \left({\alpha }_{dc}\right)}$$

(3)

where L is the synthetic aperture length, $\lambda$ is the wavelength at the transmitted frequency, $R_a$ is the distance from the antenna phase center (APC) to the scene center, $K_a$ is the beam broadening factor, v is the sensor velocity, ${\rho }_a$ is the cross-range resolution, and ${\alpha }_{dc}$ is the antenna cone angle, which is the antenna squint angle and is assumed to be 90 degrees throughout this paper. For the rest of this paper, it is convenient to assume that, in general, the radar is in a broadside condition. This assumption simplifies the subsequent mathematics. Therefore, the frame rate in the spotlight SAR mode can be represented as:

$$f_v=\frac{1}{T_a}=\frac{v·2{\rho }_a\sin \left({\alpha }_{dc}\right)}{\lambda R_a{K}_a}=\frac{v·2{\rho }_a\sin \left({\alpha }_{dc}\right)}{c{R}_a{K}_a}{f}_c$$

(4)

where $f_c$ is the transmitted frequency, and c is the speed of light. From the above equation, when the resolution and the distance to the observation point are fixed, the radar velocity or transmitted frequency should be increased in order to increase the frame rate of the SAR video. However, the radar velocity is limited by the Doppler bandwidth, which is constrained to avoid azimuth ambiguity.

Figure 3a,b shows an example of the frame rate of the ViSAR system, which is calculated using Equation (4) at $R_a$ = 1000 m and $K_a$ = 1 with various resolutions and platform velocities. As shown in Figure 3a, the frame rate is 1.003 Hz at 94 GHz in the W band, which is 9.4 times as high as it is in the X band—which includes systems such as Global Hawk or NanoSAR—where the frame rate is 0.107 Hz at 10 GHz, according to Equation (4). Therefore, the frame rate can be increased significantly, by increasing the transmitted frequency. Additionally, a higher radar velocity leads to higher frame rate. For example, two times higher frame rates can be achieved by increasing the platform velocity from 20 m/s to 40 m/s; i.e., frame rates are increased from 1.003 Hz to 2.005 Hz, at 94 GHz. However, in conventional SARs, the radar velocity is limited, to prevent Doppler ambiguities from occurring. At this time, if the MCRA is applied and the number of receiving channels is increased, Doppler ambiguities can be eliminated, even if the Doppler bandwidth increases due to the increase in the radar velocity. Therefore, the radar platform velocity can be increased without increasing Doppler ambiguities, by increasing the number of receiving channels using the MCRA.

In summary, according to Equation (4), the frame rate in the circular path can be increased by increasing the transmitted frequency or the platform velocity while maintaining the azimuth resolution. Pulse repetition frequency (PRF) is proportional to the frame rate, since this is proportional to the platform velocity. As the platform velocity increases, the increased Doppler bandwidth requires an increased PRF. Unfortunately, the increased PRF in FMCW SAR systems causes the transmission time to decrease, which leads to a reduction in detection distance. However, by using a multi-channel reconstruction algorithm, the image rate can be increased without increasing the PRF at a given azimuth resolution, by increasing the platform velocity.

By using the spotlight SAR mode for the proposed MIMO ViSAR system, it is possible to generate a SAR video with a high frame rate in the circular path. In the system proposed in this paper, in order to increase the frame rate in the spotlight mode, the transmitted frequency and the radar velocity are increased using the frame rate relation shown in Equation (4). In this case, a high frame rate SAR video can be obtained without using the full aperture synthesis method (BPA), which has very high computational complexity. In particular, the Doppler bandwidth is increased due to the increase in the radar velocity, and the MCRA algorithm is used to suppress Doppler ambiguities.

2.3. Image Size

This section describes the image size of ViSAR. The image size is limited by the Doppler bandwidth of the antenna beamwidth. With spotlight SAR, the image size is determined by the beamwidth. On the other hand, in the case of stripmap SAR, image size is determined by the pulse repetition interval (PRI) in pulsed SAR operation, or by the bandwidth of the dechirp signal in FMCW SAR operation. In the case of a ViSAR mode that is operated using spotlight SAR on a circular path, the received signal is the dechirped azimuth signal. The Doppler bandwidth is limited by scene size or antenna beamwidth as follows ([2], p. 44):

$$B_a\approx \frac{2v{W}_a\sin {\alpha }_{dc}}{\lambda R_a}$$

(5)

where ${\theta }_a\approx \frac{W_a}{R_a}$ approximately corresponds to the antenna beamwidth in azimuth and $W_a$ is the azimuth size of the scene area. The Doppler bandwidth is therefore proportional to both the radar velocity and the image size in the azimuth. According to the Nyquist theorem, the PRF of conventional SAR should be greater than the Doppler bandwidth. Figure 4 shows an example of the relationship between the image size and the Doppler bandwidth described by Equation (5), with v = 20 m/s, and $R_a$ = 1000 m. Note that, for example, the Doppler frequency of a scatterer located at the radius of 30 m is 376 (=752/2) Hz in this case. In order to maximize the effective image area, the antenna beamwidths in the azimuth and elevation directions should be of the same order [23].

When the SAR image is synthesized using the PFA, the image size is limited by wave front curvature, since the algorithm uses the plane-wave approximation. Therefore, these characteristics should be taken into consideration in the design process. The maximum image size can be increased by using wave front curvature compensation methods, as in [33,34,35]. In PFA, the scene size is limited by range curvature, and residual video phase ([2], Equation (3.130), [36], Equation (B.23)).

(a)

Scene size (diameter) is limited by range curvature as follows:

$$S<2{\rho }_a\sqrt{\frac{2R_a}{\lambda }}$$

(6)

(b)

Scene size is limited by residual video phase (RVP) ([36] (Equation (B.26)), when the chirp rate is very high, as follows:

$$S<2{\rho }_a\frac{f_c}{\sqrt{\frac{k_r}{\pi }}}$$

(7)

where $k_r$ is the chirp rate in range.

Figure 5 illustrates an example of the scene sizes generated using the PFA, with $R_a$ = 1000 m and $f_c$ = 94 GHz, constrained by wave front curvature according to Equation (6). Therefore, the antenna beamwidth should be determined prior to operation so that it corresponds to the required image size. The scene size can be converted to beamwidth limit.

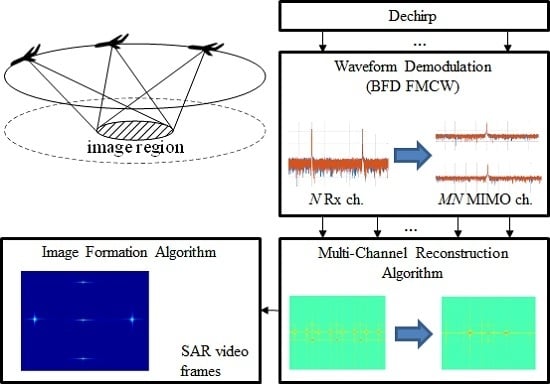
3. Signal Processing

This section describes the signal model and signal processing procedure of the proposed MIMO ViSAR system.

3.1. Geometric Models

The collection geometry of a ViSAR system operating on a circular flight path is shown in Figure 6. The radar moves along a circular flight path at a constant speed, v. $R_b$ is the radius of the flight path, $R_a$ is the slant range between the radar and the scene center, $R_z$ denotes the altitude of the aircraft, ${\theta }_a$ is the azimuth beamwidth of the antenna, ${\theta }_g$ is the grazing angle between the antenna beam axis and the ground plane, and $R_t=\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ is the radius of the scene area.

Figure 7 illustrates the antenna geometry of the proposed MIMO ViSAR system. We suppose that there are M Tx antennas and N Rx antennas. We assume in this paper that, in general, the virtual array formed by the MIMO antenna is a uniform linear array in the azimuth. Therefore, a large co-array can be realized using the MIMO concept. Also, it is advantageous to increase the number of phase centers if M and N are greater than two, since M Tx antennas and N Rx antennas give $MN$ antenna elements in the virtual array.

3.2. Signal Model

Two types of signal models are formulated in two different domains: the fast time–slow time domain and the fast time–azimuth angle domain. First, we derive the signal model in the fast time–slow time domain. We then translate this model into the fast time-azimuth angle domain. As the fast time–azimuth angle domain is based on the MIMO radar signal model, it can be used more conveniently in subsequent signal processing steps.

Figure 8 shows the generic MIMO video SAR model [25]:

In the system model, a broadside, uniform spatial sampling condition is assumed. Therefore, the PRF is selected such that the following relationship is satisfied [6]:

$$f_p=\frac{v}{MN·\Delta x}$$

(8)

where $f_p$ is the sweep repetition frequency, and $\Delta x$ is the distance between antenna elements of the virtual array.

• Signal model in the fast time–slow time domain.

In this sub-section, we define the transmitted waveform of the proposed MIMO ViSAR, and derive the received signal, the reference signal for dechirping in fast time, and the dechirped signal in the fast time–slow time domain.

The transmitted waveform vector of the proposed MIMO ViSAR system can be expressed in vector form as [3]:

$${\mathbf{s}}_T\left(t,t_a\right)\equiv \left[\begin{array}{c}s{s}_0\left(t,t_a\right)\\ ⋮\\ s{s}_m\left(t,t_a\right)\\ ⋮\\ s{s}_{M-1}\left(t,t_a\right)\end{array}\right]$$

(9)

where the transmitted signal of the m-th Tx antenna, $s{s}_m\left(t,t_a\right)$, is the BFD FMCW waveform [28] and can be written in complex form as follows:

$$s{s}_m\left(t,t_a\right)=\mathrm{rect}\left(\frac{t-t_a}{T_d}\right)\exp \left[j2\pi \left(f_c+m\Delta f_b\right)\left(t-t_a\right)+j\pi k_r{\left(t-t_a\right)}^2\right]$$

(10)

where $t_a=n_s{T}_d$ is slow time, $n_s$ is the sweep number, t is the time variable, $B_r$ and $T_d$ are the bandwidth and sweep duration of the BFD FMCW waveform, respectively, and $k_r=\frac{B_r}{T_d}$, which is the chirp rate of the waveform.

The beat frequency division offset, which means the frequency offset between the transmitted signals, should be decided such that the orthogonality within the range swath is maintained as follows:

$$\Delta f_b>\frac{B_r}{(MN-1)T_d}\frac{2R_{sw}}{c}$$

(11)

where $R_{sw}$ is the range swath and c is the speed of light.

In the proposed MIMO ViSAR system, the signal from an ideal point scatterer, received at the th Rx antenna, is a delayed version of the transmitted signal and can be derived using convolution as [25],

$$\begin{array}{c}r{r}_n\left(t,t_a^{}\right)=\sum _{m=0}^{M-1}s{s}_m\left(t,t_a^{}\right)*h_{nm}\left(t,t_a^{}\right)=\sum _{m=0}^{M-1}{a}_{nm}s{s}_m\left(t-{\tau }_{nm}\left(x_t,y_t,z_t\right),t_a^{}\right)\hfill \\ =\sum _{m=0}^{M-1}{a}_{nm}\mathrm{rect}\left(\frac{t-t_a-{\tau }_{nm}\left(x_t,y_t,z_t\right)}{T_d}\right)\hfill \\ ·\exp \left[j2\pi \left(f_c+m\Delta f_b\right)\left(t-{\tau }_{nm}\left(x_t,y_t,z_t\right)\right)+j\pi k_r{\left(t-t_a-{\tau }_{nm}\left(x_t,y_t,z_t\right)\right)}^2\right]\hfill \end{array}$$

(12)

where, $a_{nm}$ denotes the complex coefficient representing the scattering and the path loss, $h_{nm}\left(t,t_a\right)$ is the ideal channel impulse response between the n-th Rx antenna and the m-th Tx antenna, and ${\tau }_{nm}\left(x_t,y_t,z_t\right)$ is the round trip time delay from the m-th Tx antenna to the point target at position $\left(x_t,y_t,z_t\right)$ and from the point target to the n-th Rx antenna.

The reference signal for dechirping in fast time, which is a replica of the transmitted waveform delayed by the time to the center of the swath, can be written as,

$$\begin{array}{c}s{s}_{ref}\left(t,t_a\right)\hfill \\ =s{\left.s_m\left(t-{\tau }_{ref},t_a\right)\right|}_{m=0}\hfill \\ =\mathrm{rect}\left(\frac{t-t_a-{\tau }_{ref}}{T_{d,ref}}\right)\exp \left[j2\pi f_c\left(t-t_a-{\tau }_{ref}\right)+j\pi k_r{\left(t-t_a-{\tau }_{ref}\right)}^2\right]\hfill \end{array}$$

(13)

where, ${\tau }_{ref}$ is the reference delay time to the center of the swath, and $T_{d,ref}$ is the sweep duration of the reference signal.

The dechirp-on-receive technique is widely used with FMCW systems. The dechirped signal that results from mixing the received signal in Equation (12) with the reference signal in Equation (13) is:

$$\begin{array}{c}r{r}_{n,dc}\left(t,t_a\right)=r{r}_n\left(t,t_a\right)s{s}_{ref}^{*}\left(t,t_a\right)\hfill \\ =\sum _{m=0}^{M-1}{a}_{nm}\mathrm{rect}\left(\frac{t-t_a-{\tau }_{nm}}{T_d}\right)·\mathrm{rect}\left(\frac{t-t_a-{\tau }_{ref}}{T_{d,ref}}\right)\hfill \\ ·\exp \left[j2\pi \left(m\Delta f_b-k_r\left({\tau }_{nm}-{\tau }_{ref}\right)\right)\left(t-t_a-{\tau }_{nm}\right)\right]·\exp \left[-j\pi k_r{\left({\tau }_{nm}-{\tau }_{ref}\right)}^2\right]\hfill \\ ·\exp \left[-j2\pi f_c\left({\tau }_{nm}-{\tau }_{ref}\right)\right]\hfill \end{array}$$

(14)

The round-trip range from the m-th Tx antenna to a point scatterer and to the n-th Rx antenna, can be expanded and approximated using Taylor series expansion as,

$$\begin{array}{c}{r}_{n,m}\left(t;r_0\right)=c\frac{{\tau }_{nm}}{2}=r_0\sqrt{1+{\left({\displaystyle \frac{vt-\Delta x_{tx,m}}{r_0}}\right)}^2}+r_0\sqrt{1+{\left({\displaystyle \frac{vt-\Delta x_{rx,n}}{r_0}}\right)}^2}\hfill \\ \approx r_0\sqrt{1+{\left({\displaystyle \frac{v{t}_a-\Delta x_{tx,m}}{r_0}}\right)}^2}+r_0\sqrt{1+{\left({\displaystyle \frac{v{t}_a-\Delta x_{rx,n}}{r_0}}\right)}^2}\hfill \\ \approx r_0\left(1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{v{t}_a-\Delta x_{tx,m}}{r_0}}\right)}^2\right)+r_0\left(1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{v{t}_a-\Delta x_{rx,n}}{r_0}}\right)}^2\right)\hfill \\ =2r_0+\frac{v^2{\left(t_a-{\displaystyle \frac{\Delta x_{tx,m}+\Delta x_{rx,n}}{2v}}\right)}^2}{r_0}+{\displaystyle \frac{{\left(\Delta x_{tx,m}-\Delta x_{rx,n}\right)}^2}{4r_0}}\hfill \end{array}$$

(15)

where, $r_0$ is the closest distance between the antenna and the scatterer, $\Delta x_{tx,m}$ is the distance between the reference Tx antenna and the m-th Tx antenna, and $\Delta x_{rx,n}$ is the distance between the reference Rx antenna and the n-th Rx antenna. The range can be interpreted as a phase given by:

$$\begin{array}{c}\frac{2\pi }{\lambda }{r}_{n,m}\left(t;r_0\right)\hfill \\ ={\displaystyle \frac{2\pi }{\lambda }}\left[2r_0+\frac{v^2{\left(t_a-{\displaystyle \frac{\Delta x_{tx,m}+\Delta x_{rx,n}}{2v}}\right)}^2}{r_0}+{\displaystyle \frac{{\left(\Delta x_{tx,m}-\Delta x_{rx,n}\right)}^2}{4r_0}}\right]\hfill \\ =\frac{4\pi }{\lambda }{r}_0+{\displaystyle \frac{2\pi }{\lambda }}{\displaystyle \frac{v^2{\left(t_a-{\displaystyle \frac{\Delta x_{tx,m}+\Delta x_{rx,n}}{2v}}\right)}^2}{r_0}}+{\displaystyle \frac{\pi {\left(\Delta x_{tx,m}-\Delta x_{rx,n}\right)}^2}{2\lambda r_0}}\hfill \end{array}$$

(16)

where $\lambda$ is the wave length.

After substituting Equation (15) or (16) into Equation (14), the dechirped signal at the n-th Rx channel can be rewritten as,

$$\begin{array}{c}r{r}_{n,dc}\left(t_r,t_a\right)\hfill \\ \approx \sum _{m=0}^{M-1}{a}_{nm}\mathrm{rect}\left({\displaystyle \frac{t_r-{\tau }_{nm}}{T_d}}\right)·\mathrm{rect}\left({\displaystyle \frac{t_r-{\tau }_{ref}}{T_{d,ref}}}\right)\hfill \\ ·\exp \left[j2\pi m\Delta f_b\left(t_r-{\tau }_0\right)\right]\hfill \\ ·\exp \left[-j2\pi k_r\left(t_r-{\tau }_0\right)\left({\tau }_0-{\tau }_{ref}\right)-j\pi k_r{\left({\tau }_0-{\tau }_{ref}\right)}^2\right]\hfill \\ ·\exp \left[-j{\displaystyle \frac{4\pi }{\lambda }}{r}_0-j{\displaystyle \frac{2\pi }{\lambda }}{\displaystyle \frac{v^2{\left(t_a-{\displaystyle \frac{\Delta x_{tx,m}+\Delta x_{rx,n}}{2v}}\right)}^2}{r_0}}-j{\displaystyle \frac{\pi {\left(\Delta x_{tx,m}-\Delta x_{rx,n}\right)}^2}{2\lambda r_0}}\right]\hfill \\ ·\exp \left(j2\pi f_d{t}_r\right)·\exp \left(j2\pi f_c{\tau }_{ref}\right)\hfill \end{array}$$

(17)

where, $t_r=t-t_a$ is fast time, ${\tau }_0$ is the time delay corresponding to $r_0$, and $f_d$ is the Doppler frequency shift within the transmission of one sweep. $f_d$ results from the continuous antenna motion of the platform, since the traditional stop-and-go approximation is not valid for FMCW SAR [11]. In Equation (17), the first exponential term is the frequency and phase shift due to the BFD offset. The second exponential term represents the range signal including the RVP component, which is the second term in the square brackets. The third exponential term is the azimuth phase history of the proposed MIMO ViSAR. The fourth exponential term represents the Doppler shift due to continuous antenna motion within one sweep. The fifth exponential term is the phase delay corresponding to the time delay to the scene center.

Therefore, the vector of a dechirped received signal in the proposed MIMO ViSAR system can be expressed as:

$${\mathbf{r}}_R\left(t_r,t_a\right)\equiv \left[\begin{array}{c}r{r}_{0,dc}\left(t_r,t_a\right)\\ ⋮\\ r{r}_{n,dc}\left(t_r,t_a\right)\\ ⋮\\ r{r}_{N-1,dc}\left(t_r,t_a\right)\end{array}\right]$$

(18)

• Signal model in the fast time–azimuth angle domain.

This model is convenient for understanding the subsequent signal processing steps of the MCRA, as it is implemented in the fast time–azimuth frequency domain. The model has a close relationship with the digital beamforming technique mentioned in [7]. The received signal can be expressed using a steering vector in the azimuth angle domain. This signal model explicitly shows the relationship between the digital beamforming techniques used for Tx and Rx in the proposed MIMO ViSAR system.

The relationship between the azimuth frequency domain, $f_a$, and the azimuth angle domain, $\theta$, is as follows [7]:

$$f_a=\frac{2v}{\lambda }\sin \theta$$

(19)

The azimuth time delay term in Equation (17) can be expressed in the azimuth frequency domain, using the Fourier transform property as:

$$b_n\left(f_a\right)a_m\left(f_a\right)=2\pi f_a\frac{\Delta x_{tx,m}+\Delta x_{rx,n}}{2v}$$

(20)

which can be written in the azimuth angle domain using Equation (19) as:

$$\begin{array}{c}{b}_n\left(\theta \right)a_m\left(\theta \right)\hfill \\ =2\pi f_a{\displaystyle \frac{\Delta x_{tx,m}+\Delta x_{rx,n}}{2v}}\hfill \\ =2\pi \left({\displaystyle \frac{2v}{\lambda }}\sin \theta \right){\displaystyle \frac{\Delta x_{tx,m}+\Delta x_{rx,n}}{2v}}\hfill \\ ={\displaystyle \frac{2\pi \left(\Delta x_{tx,m}+\Delta x_{rx,n}\right)}{\lambda }}\sin \theta \hfill \end{array}$$

(21)

where $a_m\left(\theta \right)$ are individual elements of the Tx steering vector, $\mathbf{a}\left(\theta \right)$, and are given by:

$$a_m\left(\theta \right)=\frac{2\pi \Delta x_{tx,m}}{\lambda }\sin \theta$$

(22)

and $b_n\left(\theta \right)$ are individual elements of the Rx steering vector, $\mathbf{b}\left(\theta \right)$, and are given by:

$$b_n\left(\theta \right)=\frac{2\pi \Delta x_{rx,n}}{\lambda }\sin \theta$$

(23)

The Tx steering vector, $\mathbf{a}\left(\theta \right)$, can be expressed as an $M\times 1$ vector [3]:

$$\mathbf{a}\left(\theta \right)\equiv \left[\begin{array}{c}\frac{2\pi }{\lambda }\Delta x_{tx,0}\sin \theta \\ ⋮\\ \frac{2\pi }{\lambda }\Delta x_{tx,m}\sin \theta \\ ⋮\\ \frac{2\pi }{\lambda }\Delta x_{tx,M-1}\sin \theta \end{array}\right]$$

(24)

and the Rx steering vector, $\mathbf{b}\left(\theta \right)$, can be expressed as an $N\times 1$ vector:

$$\mathbf{b}\left(\theta \right)\equiv \left[\begin{array}{c}\frac{2\pi }{\lambda }\Delta x_{rx,0}\sin \theta \\ ⋮\\ \frac{2\pi }{\lambda }\Delta x_{rx,n}\sin \theta \\ ⋮\\ \frac{2\pi }{\lambda }\Delta x_{rx,N-1}\sin \theta \end{array}\right]$$

(25)

Therefore, after applying the Fourier transform in the azimuth frequency domain to Equation (17), the dechirped signal can be written as:

$$\begin{array}{c}r{R}_{n,dc}\left(t_r,f_a\right)\hfill \\ ={\mathrm{F}}_{\mathrm{a}}\left[r{r}_{n,dc}\left(t_r,t_a\right)\right]\hfill \\ =b_n\left(f_a\right)\sum _{m=0}^{M-1}{a}_{nm}\mathrm{rect}\left({\displaystyle \frac{t_r-{\tau }_{nm}}{T_d}}\right)·\mathrm{rect}\left({\displaystyle \frac{t_r-{\tau }_{ref}}{T_{d,ref}}}\right)\hfill \\ ·\exp \left[j2\pi m\Delta f_b\left(t_r-{\tau }_0\right)\right]\hfill \\ ·\exp \left[-j2\pi k_r\left(t_r-{\tau }_0\right)\left({\tau }_0-{\tau }_{ref}\right)-j\pi k_r{\left({\tau }_0-{\tau }_{ref}\right)}^2\right]\hfill \\ ·\exp \left[-j{\displaystyle \frac{4\pi }{\lambda }}{r}_0-j{\displaystyle \frac{\pi {\left(\Delta x_{tx,m}-\Delta x_{rx,n}\right)}^2}{2\lambda r_0}}\right]\hfill \\ ·\exp \left(j2\pi f_d{t}_r\right)·\exp \left(j2\pi f_c{\tau }_{ref}\right)\hfill \\ ·a_m\left(f_a\right)·R_{az}\left(f_a\right)\hfill \end{array}$$

(26)

where ${\mathrm{F}}_{\mathrm{a}}\left[·\right]$ is the Fourier transform operator with respect to slow time, and $R_{az}\left(f_a\right)$ is calculated as follows:

$$R_{az}\left(f_a\right)=T_a\mathrm{sinc}\left(\pi T_a\left(f_a+k_a\Delta t_a\right)\right)$$

(27)

which is the Fourier transform of the following azimuth time function, which is given by:

$$r_{az}\left(t_a\right)=\exp \left[-j2\pi k_a\Delta t_a{t}_a\right]$$

(28)

where $k_a=\frac{2v^2}{\lambda r_0}$ is the chirp rate in azimuth and $\Delta t_a$ is the differential azimuth time between the scatterer and the scene center. Note that $R_{az}\left(f_a\right)$ represents the result of the azimuth dechirping, which is implemented by geometrical steering on the circular path.

After substituting Equations (19)–(21) into Equation (26) and changing the notation, we can obtain the dechirped signal at the n-th Rx channel in the fast time–azimuth angle domain as follows:

$$\begin{array}{c}r{R}_{n,dc}\left(t_r,\theta \right)\hfill \\ \approx b_n\left(\theta \right)\sum _{m=0}^{M-1}{a}_{nm}\mathrm{rect}\left(\frac{t_r-{\tau }_{nm}}{T_d}\right)·\mathrm{rect}\left({\displaystyle \frac{t_r-{\tau }_{ref}}{T_{d,ref}}}\right)\hfill \\ ·\exp \left[j2\pi m\Delta f_b\left(t_r-{\tau }_0\right)\right]\hfill \\ ·\exp \left[-j2\pi k_r\left(t_r-{\tau }_0\right)\left({\tau }_0-{\tau }_{ref}\right)-j\pi k_r{\left({\tau }_0-{\tau }_{ref}\right)}^2\right]\hfill \\ ·\exp \left[-j{\displaystyle \frac{4\pi }{\lambda }}{r}_0\right]·\exp \left(j2\pi f_d{t}_r\right)·\exp \left(j2\pi f_c{\tau }_{ref}\right)\hfill \\ ·a_m\left(\theta \right)·R_{az}\left(\theta \right)\hfill \\ \equiv b_n\left(\theta \right)\sum _{m=0}^{M-1}r{R}_{m,dc}\left(t_r,\theta \right)·a_m\left(\theta \right)\hfill \end{array}$$

(29)

where $r{R}_{m,dc}\left(t_r,\theta \right)$ is defined as a function of fast time and azimuth angle at the m-th Tx channel.

Therefore, in the fast time–azimuth angle domain, the dechirped signal in the N Rx channels of the proposed MIMO ViSAR system, described by Equation (29), can be compactly expressed as an $N\times 1$ vector using Equations (24) and (25) as follows [3]:

$${\mathbf{rR}}_{R,dc}\left(t_r,\theta \right)=\mathbf{b}\left(\theta \right)\mathbf{a}{\left(\theta \right)}^T{\mathbf{rR}}_{T,dc}\left(t_r,\theta \right)$$

(30)

where the dechirped signal from the M Tx channels, described in Equation (30), can be defined in the fast time–azimuth angle domain as an $M\times 1$ vector:

$${\mathbf{rR}}_{T,dc}\left(t_r,\theta \right)=\left[\begin{array}{c}r{R}_{0,dc}\left(t_r,\theta \right)\\ ⋮\\ r{R}_{M-1,dc}\left(t_r,\theta \right)\end{array}\right]=\left[\begin{array}{c}{r}_0\left(t_r\right)\\ ⋮\\ r_{M-1}\left(t_r\right)\end{array}\right]R_{az}\left(\theta \right)$$

(31)

where $r_m\left(t_r\right)$ is defined as a function of fast time as follows:

$$\begin{array}{c}{r}_m\left(t_r\right)\hfill \\ =a_{nm}\mathrm{rect}\left({\displaystyle \frac{t_r-{\tau }_{nm}}{T_d}}\right)·\mathrm{rect}\left({\displaystyle \frac{t_r-{\tau }_{ref}}{T_{d,ref}}}\right)\hfill \\ ·\exp \left[j2\pi m\Delta f_b\left(t_r-{\tau }_0\right)\right]\hfill \\ ·\exp \left[-j2\pi k_r\left(t_r-{\tau }_0\right)\left({\tau }_0-{\tau }_{ref}\right)-j\pi k_r{\left({\tau }_0-{\tau }_{ref}\right)}^2\right]\hfill \\ ·\exp \left[-j\frac{4\pi }{\lambda }{r}_0\right]·\exp \left(j2\pi f_d{t}_r\right)·\exp \left(j2\pi f_c{\tau }_{ref}\right)\hfill \end{array}$$

(32)

and $R_{az}\left(\theta \right)$ is calculated in the azimuth angle domain from $R_{az}\left(f_a\right)$ using Equation (27). Note that the $N\times M$ MIMO channel matrix is defined as follows [3]:

$$\mathbf{A}\left(\theta \right)=\mathbf{b}\left(\theta \right)\mathbf{a}{\left(\theta \right)}^T$$

(33)

In the case of orthogonal waveforms, the MIMO steering vector for angle $\theta$ is $\mathbf{g}\left(\theta \right)\equiv \mathrm{Vec}\left\{\mathbf{A}\left(\theta \right)\right\}$, where $\mathrm{Vec}\left\{·\right\}$ denotes the vectorization operator.

3.3. Signal Processing Procedure

Signal processing for the proposed MIMO ViSAR system proceeds in the following parts: BFD FMCW demodulation, including Doppler shift compensation, azimuth ambiguity suppression using the MCRA, and video frame formation, with image rotation to the CDU using the PFA.

The RVP terms in the dechirped signal described in Equation (32) can be ignored or compensated using the RVP correction method (“range deskew”) described in [2] as follows:

$$\begin{array}{c}{r}_{m,DRVP}\left(t_r\right)\hfill \\ =a_{nm}\mathrm{rect}\left(\frac{t_r-{\tau }_{nm}}{T_d}\right)·\mathrm{rect}\left(\frac{t_r-{\tau }_{ref}}{T_{d,ref}}\right)\hfill \\ ·\exp \left[j2\pi m\Delta f_b\left(t_r-{\tau }_0\right)\right]\hfill \\ ·\exp \left[-j2\pi k_r\left(t_r-{\tau }_0\right)\left({\tau }_0-{\tau }_{ref}\right)\right]\hfill \\ ·\exp \left[-j\frac{4\pi }{\lambda }{r}_0\right]·\exp \left(j2\pi f_d{t}_r\right)·\exp \left(j2\pi f_c{\tau }_{ref}\right)\hfill \end{array}$$

(34)

where the fourth exponential term represents the Doppler shift due to continuous antenna motion within one sweep, as mentioned earlier.

The continuous antenna motion at the n-th Rx channel is compensated by multiplying Equation (34) with the Doppler frequency correction factor giving the following expression:

$$\begin{array}{c}{r}_{m,DDOP}\left(t_r\right)\hfill \\ =r_{m,DRVP}\left(t_r\right)·\exp \left(-j2\pi f_d{t}_r\right)\hfill \\ =a_{nm}\mathrm{rect}\left(\frac{t_r-{\tau }_{nm}}{T_d}\right)·\mathrm{rect}\left(\frac{t_r-{\tau }_{ref}}{T_{d,ref}}\right)\hfill \\ ·\exp \left[j2\pi m\Delta f_b\left(t_r-{\tau }_0\right)\right]\hfill \\ ·\exp \left[-j2\pi k_r\left(t_r-{\tau }_0\right)\left({\tau }_0-{\tau }_{ref}\right)\right]\hfill \\ ·\exp \left[-j\frac{4\pi }{\lambda }{r}_0\right]·\exp \left(j2\pi f_c{\tau }_{ref}\right)\hfill \end{array}$$

(35)

where the first exponential term represents the frequency and phase offset due to BFD FMCW modulation.

Next, BFD FMCW demodulation is carried out at the n-th Rx channel in two processing steps: frequency shift and phase shift compensation. The frequency shift, which results from the beat frequency division offset, is compensated by multiplying Equation (35) with the correction factor, giving the following expression:

$$\begin{array}{c}{r}_{m,BFD1}\left(t_r\right)\hfill \\ =\exp \left(-j2\pi m\Delta f_b{t}_r\right)·r_{m,DDOP}\left(t_r\right)\hfill \\ =\exp \left(-j2\pi m\Delta f_b{t}_r\right)\exp \left[j2\pi \left\{m\Delta f_b-k_r\left({\tau }_0-{\tau }_{ref}\right)\right\}\left(t_r-{\tau }_0\right)\right]\hfill \\ ·\exp \left[-j\frac{4\pi }{\lambda }{r}_0\right]·\exp \left(j2\pi f_c{\tau }_{ref}\right)\hfill \\ =\exp \left[-j2\pi k_r\left({\tau }_0-{\tau }_{ref}\right)\left(t_r-{\tau }_0\right)\right]·\exp \left(-j2\pi m\Delta f_b{\tau }_0\right)\hfill \\ ·\exp \left[-j\frac{4\pi }{\lambda }{r}_0\right]·\exp \left(j2\pi f_c{\tau }_{ref}\right)\hfill \end{array}$$

(36)

where the second exponential term represents the phase offset due to BFD FMCW modulation.

The phase shift is then compensated by multiplying Equation (36) with the correction factor, giving the following:

$$\begin{array}{c}{r}_{m,BFD2}\left(t_r\right)\hfill \\ =r_{m,BFD1}\left(t_r\right)·\exp \left(j2\pi m\Delta f_b{\tau }_0\right)\hfill \\ =\exp \left[-j2\pi k_r\left({\tau }_0-{\tau }_{ref}\right)\left(t_r-{\tau }_0\right)\right]·\exp \left[-j\frac{4\pi }{\lambda }{r}_0\right]·\exp \left(j2\pi f_c{\tau }_{ref}\right)\hfill \end{array}$$

(37)

Therefore, using Equation (37), after BFD FMCW waveform demodulation, the signal from Equation (30) can be expressed as:

$${\mathbf{rR}}_{BFD}\left(t_r,\theta \right)=\mathbf{b}\left(\theta \right)\mathbf{a}{\left(\theta \right)}^T{\mathbf{M}}_{BFD}\left(t_r,\theta \right)$$

(38)

where the BFD FMCW waveform demodulation matrix can be defined using Equations (27) and (37) as the following $M\times M$ diagonal matrix:

$$\begin{array}{c}{\mathbf{M}}_{BFD}\left(t_r,\theta \right)\hfill \\ \equiv \left[\begin{array}{ccc}r{R}_{0,BFD2}\left(t_r,\theta \right)& 0& 0\\ 0& \ddots & 0\\ 0& 0& r{R}_{M-1,BFD2}\left(t_r,\theta \right)\end{array}\right]\hfill \\ =\left[\begin{array}{ccc}{r}_{0,BFD2}\left(t_r\right)& 0& 0\\ 0& \ddots & 0\\ 0& 0& r_{M-1,BFD2}\left(t_r\right)\end{array}\right]R_{az}\left(\theta \right)\hfill \end{array}$$

(39)

Note that each element of the matrix, ${\mathbf{rR}}_{BFD}\left(t_r,\theta \right)$, represents the signal after BFD FMCW demodulation of the corresponding elements of the virtual array.

Following a range Fourier transform of Equation (38), the $N\times M$ range compression output matrix can be obtained as follows:

$${\mathbf{RR}}_{RC}\left(f_r,\theta \right)={\int }_{-\infty }^{\infty }{\mathbf{rR}}_{BFD}\left(t_r,\theta \right)e^{-j2\pi f_r{t}_r}d{t}_r$$

(40)

where the $nm$-th element of this matrix is the Fourier transform of the dechirped transmitted signal vector, with respect to fast time, as shown in Equation (38) as follows:

$$\begin{array}{c}R{R}_{RC,nm}\left(f_r,\theta \right)\hfill \\ ={\mathrm{F}}_{\mathrm{r}}\left[r{R}_{m,BFD2}\left(t_r,\theta \right)b_n\left(\theta \right)a_m\left(\theta \right)\right]\hfill \\ ={\mathrm{F}}_{\mathrm{r}}\left[\exp \left[-j2\pi k_r\left({\tau }_0-{\tau }_{ref}\right)\left(t_r-{\tau }_0\right)\right]\right]·\exp \left[-j\frac{4\pi }{\lambda }{r}_0\right]\hfill \\ ·\exp \left(j2\pi f_0{\tau }_{ref}\right)·R_{az}\left(\theta \right)·b_n\left(\theta \right)a_m\left(\theta \right)\hfill \\ =T_d\mathrm{sinc}\left(\pi T_d\left(f_r+k_r\left({\tau }_0-{\tau }_{ref}\right)\right)\right)·\exp \left(-j2\pi {\tau }_0{f}_r\right)\hfill \\ ·\exp \left[-j\frac{4\pi }{\lambda }{r}_0\right]·\exp \left(j2\pi f_c{\tau }_{ref}\right)·R_{az}\left(\theta \right)·b_n\left(\theta \right)a_m\left(\theta \right)\hfill \end{array}$$

(41)

where ${\mathrm{F}}_{\mathrm{r}}\left[·\right]$ is the Fourier transform operator with respect to fast time. Using the fast time relationship, $t_r=\frac{T_d}{B_r}{f}_r$, and the range relationship, $r=\frac{c{T}_d}{2B_r}{f}_r$, we can define the point spread function in range as follows:

$${\delta }_r\left(r\right)\equiv {\left.T_d\mathrm{sinc}\left(\pi T_d{f}_r\right)\right|}_{f_r=\frac{2B_r}{c{T}_d}r}$$

(42)

It is also assumed that all targets exist only within the range swath. The $MN\times 1$ range compression vector, which is output from the virtual array, is given from Equation (40) as [3],

$$\begin{array}{c}\mathbf{w}\left(f_r,\theta \right)\hfill \\ \equiv \mathrm{Vec}\left\{{\mathbf{RR}}_{RC}\left(f_r,\theta \right)\right\}\hfill \\ =\left[\begin{array}{c}{w}_0\left(f_r,\theta \right)\\ ⋮\\ w_l\left(f_r,\theta \right)\\ ⋮\\ w_{MN-1}\left(f_r,\theta \right)\end{array}\right]\hfill \end{array}$$

(43)

Using Equations (19), (41) and (42), this equation is represented in the range-azimuth frequency domain, $\left(r,f_a\right)$, as:

$$\begin{array}{c}\mathbf{w}\left(r,f_a\right)\hfill \\ ={\delta }_r\left(r-\left(r_0-R_a\right)\right)·\exp \left(-j2\pi \frac{4B_r{r}_0}{c^2{T}_d}r\right)\hfill \\ ·\exp \left[-j\frac{4\pi }{\lambda }\left(r_0-R_a\right)\right]·R_{az}\left(f_a\right)·g\left(f_a\right)\hfill \end{array}$$

(44)

This equation represents $MN$ channel data of the virtual array formed by BFD FMCW demodulation described above, without taking into account the azimuth ambiguities. When the azimuth ambiguities are considered, the signal from the $MN$ virtual elements can be expressed as an $MN\times 1$ vector, using Equation (44), as follows [9]:

$$\begin{array}{c}\mathbf{c}\left(r,f_a^{}\right)=\left\{\sum _{l=0}^{MN-1}{\delta }_r\left(r-\left(r_0-R_a\right)\right)·\exp \left(-j2\pi \frac{4B_r{r}_0}{c^2{T}_d}r\right)·\exp \left[-j\frac{4\pi }{\lambda }\left(r_0-R_a\right)\right]\right.\hfill \\ \left.·R_{az}\left(f_a+l{f}_p\right)·\mathrm{\Phi }\left(f_a+l{f}_p\right)\right\}·{\mathbf{1}}_{MN}\hfill \end{array}$$

(45)

where $l=0,\cdots ,MN-1$ is the ambiguity number, and ${\mathbf{1}}_{MN}={\left[\begin{array}{cccc}1& 1& \cdots & 1\end{array}\right]}^T$ is the vector of $MN$ ones. The $MN\times MN$ channel phase delay matrix is a diagonal matrix whose elements can be defined as, ${\left(\mathrm{\Phi }\left(f_a\right)\right)}_{k,k}=g_k\left(f_a\right)$, where $g_k\left(f_a\right)$ is k-th element of the MIMO steering vector, $\mathbf{g}\left(f_a\right)$. In Equation (45), we assume ideal and identical patterns for all antennas. This equation is included here for completeness of the signal processing procedure. The measured $MN\times 1$ multi-channel signal vector is equal to:

$$\mathbf{z}\left(r,f_a^{}\right)=\mathbf{c}\left(r,f_a^{}\right)+\mathbf{n}\left(r,f_a^{}\right)$$

(46)

where $\mathbf{n}\left(r,f_a\right)$ is the noise vector. As mentioned in the introduction, there are many reconstruction algorithms. In the following, the matrix inversion method [9] is described due to the simplicity of its implementation. The reconstruction filters can be calculated through minimization as [9]:

$$F_M=\underset{{\mu }_p\left(f_d\right)}{\min }∥z_{org}\left(r,t_a\right)-z_{rec}^{}\left(r,t_a\right)∥$$

(47)

where $∥·∥$ denotes the L${}_2$ norm and $z_{org}\left(r,t_a\right)$ is the original signal, sampled at a frequency of $MN·f_p$. The reconstructed signal is obtained as:

$$z_{rec}\left(r,f_a^{}+l{f}_p\right)={\mu }_p\left(f_a^{}\right)\mathbf{z}\left(r,f_a^{}\right)$$

(48)

where $\mathbf{z}\left(r,f_a\right)$ is the multi-channel data given by:

$$\mathbf{z}\left(r,f_a^{}\right)={\left[\begin{array}{cccc}{z}_0\left(r,f_a^{}\right)& z_1\left(r,f_a^{}\right)& \cdots & z_{MN-1}\left(r,f_a^{}\right)\end{array}\right]}^T$$

(49)

and the reconstruction filter can be written as:

$${\mu }_l\left(f_a^{}\right)={\mathbf{H}}_{inv}^H·{\mathbf{1}}_{MN}^l$$

(50)

where the superscript, ${}^H$, denotes the Hermitian transpose, and ${\mathbf{1}}_{MN}^l={\left[\begin{array}{cccccc}0& 0& \cdots & 1& \cdots & 0\end{array}\right]}^T$ is an $MN\times 1$ vector of zeros except for the $l+1$th position which contains a one, and,

$${\mathbf{H}}_{inv}\left(f_a^{}\right)=\mathbf{H}{\left(f_a^{}\right)}^{-1}$$

(51)

$$\mathbf{H}\left(f_a^{}\right)=\left[\begin{array}{cccc}{\mathbf{g}}_0\left(f_a^{}\right)& {\mathbf{g}}_1\left(f_a^{}\right)& \cdots & {\mathbf{g}}_{MN-1}\left(f_a^{}\right)\end{array}\right]$$

(52)

$${\mathbf{g}}_l\left(f_a^{}\right)=\mathrm{Vec}\left\{\mathbf{A}\left(f_a+l{f}_p\right)\right\}$$

(53)

Note that, as mentioned in [7], in the case of a single-platform system or collocated antennas, the columns of the channel matrix, $\mathbf{H}\left(f_a\right)$, consist of the steering vectors, ${\mathbf{g}}_l\left(f_a\right)$.

After reconstruction, SAR video frames are formed by the PFA, with $z_{rec}\left(r,f_a+l{f}_p\right)$ as input data. In the circular path case, image rotation is implemented in the frequency domain using Equation (54), so that the image is in a fixed orientation. This orientation is called the cardinal direction. Image rotation is performed in the frequency domain to reduce distortion. Rotation proceeds as follows:

$${\mathbf{k}}_{CDU}=\mathbf{R}·{\mathbf{k}}_{FRU}$$

(54)

where ${\mathbf{k}}_{CDU}$ is the spatial frequency vector in the cardinal direction up (CDU) coordinate system (global coordinate), ${\mathbf{k}}_{FRU}$ is the spatial frequency vector in the far range up (FRU) coordinate system (local coordinate), and the rotation matrix is defined as follows:

$$\mathbf{R}=\left[\begin{array}{cc}\cos {\theta }_{as}& \sin {\theta }_{as}\\ -\sin {\theta }_{as}& \cos {\theta }_{as}\end{array}\right]$$

(55)

where ${\theta }_{as}$ is the aspect angle with respect to the cardinal direction, as shown in Figure 2.

A block diagram of signal processing procedures in the proposed ViSAR system is shown in Figure 9. The first part of signal processing is BFD waveform demodulation, which includes Doppler compensation. In the second part, the MCRA [6,7,8,9] is implemented. In the third part, the PFA is used for SAR video frame formation, including image rotation in the 2D spatial frequency domain.

4. Simulation Results

In this section, we design an exemplary MIMO video SAR system based on BFD FMCW. The performance of the proposed system is evaluated in terms of peak sidelobe ratio (PSLR), resolution, image size, and frame rate, using numerical simulations. As well as antenna parameters, other system and geometric parameters are chosen according to traditional rules, such as the radar equation, or to mirror parameters of existing systems.

4.1. System Parameters

The transmitted frequency is selected to get a higher frame rate as dictated by Equation (4). When considering commercial availability of RF components, 94 GHz is an acceptable frequency for small UAVs. A one-millisecond sweep duration corresponds to a PRF of 1 kHz. According to the Nyquist theorem, the PRF of conventional FMCW SAR systems should be greater than the Doppler bandwidth. However, the PRF of the proposed system can be chosen to be 4000/4 Hz, using four virtual array channels consisting of two Tx and two Rx channels (M = 2, N = 2). To ensure a slant range resolution of 0.15 m, a chirp bandwidth of 1 GHz is necessary. The beat frequency offset is selected to be 2 MHz for an 80-m range swath width or scene size, based on calculations using Equation (11). The sampling frequency for analog-to-digital conversion (ADC) of the proposed system and a reference single channel ViSAR system are, 4 MHz, and 2 MHz, respectively.

To achieve the required resolution in the azimuth, the integration angle of the synthetic aperture should be greater than 1.14°. The integration angle in this simulation is 1.17°. To observe the required scene size, the transmitting and receiving antenna beamwidth can be chosen to 4°. The distance between Tx antennas is 0.04 m. The distance between Rx antennas is 0.02 m. System parameters are selected such that uniform spatial sampling is applied, as defined by Equation (8). The distance between the phase centers in the virtual array is 0.02 m. In the single channel ViSAR system, the receiving antenna is identical to the transmit antenna. In the MIMO ViSAR system, the transmitting and receiving antennas are placed in the azimuth.

Table 1. System parameters. ViSAR: video synthetic aperture radar.

Parameters	MIMO ViSAR	Single Channel ViSAR
Transmitted frequency	94 GHz	94 GHz
Bandwidth	1 GHz	1 GHz
Slant range to scene center	1000 m	1000 m
Operation velocity	40 m/s	20 m/s
Scene size	80 m	40 m
Resolution	0.15 × 0.08 m	0.15 × 0.08 m
Radar losses	10 dB	10 dB
Number of transmit apertures	2	1
Number of receive apertures	2	1
Transmit antenna gain	15 dB	15 dB
Receive antenna gain	15 dB	15 dB
Sweep duration	1 msec	1 msec
Sampling frequency	4 MHz	2 MHz

lists technical and geometric parameters of both systems investigated. The operation velocities of 20 m/s and 40 m/s are selected considering those of commercial or military UAVs such as NEO S-300 by Swiss UAV [37] and RQ-7 Shadow 200 by AAI [38]. As mentioned in Section 2.2, two times higher operation velocity of the proposed system is applied to increase the frame rate due to its proportionality to the platform velocity.

Figure 10 shows an illustration of the block diagram for the proposed MIMO video SAR system, with two Tx and two Rx channels. As described in Section 3, there are four channels in the equivalent virtual array in this case.

4.2. Point Target Simulation

In this sub-section, a single point target simulation, developed in MATLAB with the system parameters listed in Table 1, is used to verify the performance of the proposed MIMO ViSAR system under ideal sensor motion conditions. Figure 11 illustrates the collection geometry, including the target location, for a circular path simulation. Ideal patterns are assumed for all antennas.

The transmitted waveforms are generated using Equation (9) and (10), with $\Delta f_b$ = 2 MHz, $B_r$ = 1 GHz, and $T_d$ = 1 ms. The reference signal for dechirping in fast time was simulated as the delayed version of the transmitted signal at Tx channel 1 using Equation (13). ${\tau }_{ref}$ was set to 6.67 $\mathsf{\mu }$s in this simulation, which corresponds to the time delay to the scene center. The signal processing procedures presented in Section 3.3 are simulated using the scene geometry and the parameters of the MIMO ViSAR system listed in Table 1.

RVP terms can be ignored for the parameters used in this simulation. The continuous antenna motion effect for FMCW is compensated using Equation (35).

BFD FMCW demodulation is shown in Figure 12. Figure 12a,b shows the signal in range-frequency domain before and after BFD FMCW demodulation, respectively. Note that in Figure 12a, the responses to different transmitters are separated by the beat frequency division offset, 2 MHz. Due to this spectral separation, transmitted waveforms from each Tx antenna can be distinguished. BFD FMCW demodulation is implemented using the frequency shift compensation detailed by Equation (36), and the phase compensation detailed by Equation (37), as described in Section 3.3.

Since two Tx and two Rx channels are used, there are four channels in the virtual array formed by MIMO technology after demodulation, as shown in Figure 12. The distance between the phase centers in the virtual array is 0.02 m. The distance between Tx antennas is 0.04 m, and the distance between Rx antennas is 0.02 m. In this case, uniform spatial sampling is applied according to Equation (8).

Azimuth spectrum reconstruction is shown in s Figure 13 and Figure 14. Figure 13a,b show the azimuth aliasing spectrum of the first channel (l = 0) in the proposed MIMO ViSAR system before the reconstruction filters.

The azimuth spectrum is completely reconstructed, after applying the reconstruction filters of the MCRA, ${\mathit{\mu }}_0\left(f_a\right)$, ${\mathit{\mu }}_1\left(f_a\right)$, ${\mathit{\mu }}_2\left(f_a\right)$ and ${\mathit{\mu }}_3\left(f_a\right)$, as shown in Equation (50), to the data received by the four MIMO channels, respectively, and stitching all four output signals together, as shown in Figure 14. Note that the azimuth frequency axis is expanded to four times its magnitude before applying the MCRA. The MCRA coherently combines the four channel signals in the azimuth and reconstructs a 4 kHz Doppler spectrum, which is four times wider than the single channel signal.

Figure 15 plots the simulated 2D SAR image (video frame) of the impulse response function of a point target. Figure 15b shows the contour plot at −3, −6, −9, −30 dB from the peak level.

The results of impulse response analysis in the down-range and cross-range are shown in Figure 16a,b respectively. The resolutions at −3.9 dB from the peak level are 0.149 m in the down-range, and 0.081 m in the cross-range. The PSLRs are −13.42 dB in the down-range, and −13.41 dB in the cross-range. No windows are applied for sidelobe reduction, which means $K_a$ = 1 at −3.9 dB.

A simulation with multiple synthetic point targets is used to verify the improvements in the frame rate and the image size achieved by the proposed MIMO ViSAR system, by suppressing azimuth ambiguities using MCRA. The five targets are located within a maximum of 30 m from the scene center, as shown in Figure 17.

As shown in Figure 5, the maximum scene size of the PFA, which, according to Equation (6), is limited by wave front curvature, is 126.7 m, when $R_a$ = 1000 m and $f_c$ = 94 GHz. As shown in Figure 4, the Doppler bandwidth is proportional to the image size. The Doppler bandwidths for 2°-wide azimuth beamwidths are 437 Hz, and 1750 Hz for v = 20 m/s, and 80 m/s, respectively. The Doppler bandwidths for 4°-wide azimuth beamwidths are 874 Hz, and 1750 Hz for v = 20 m/s, and 40 m/s, respectively. Therefore, a wider image size requires a wider Doppler bandwidth, which results in the need for a higher PRF in the FMCW SAR system. According to Equation (5), when the frame rate and the image size are increased by a factor of two, the Doppler bandwidth is four times wider. Thus, a four-times-higher PRF is required, which is 4 kHz for the system under investigation. In this case, increases to both the frame rate and image size can be achieved through the suppression of Doppler ambiguities in the azimuth spectrum, with the application of the MCRA, while maintaining the same PRF, which is 1 kHz.

The dechirped azimuth signal, gotten after BFD FMCW demodulation is performed in this multiple point target simulation, is shown in Figure 18. The SAR signal on the circular path is azimuth dechirped as described in Section 3.2. Scatterers farther from the scene center have a higher Doppler frequency, which is proportional to the scene size, according to Equation (27). We observe three azimuth ambiguities for each target in Figure 18 ($l=1,2,3$). Due to these azimuth ambiguities, the ambiguous azimuth frequency of Scatterer E is measured as 248.3 Hz, as shown in Figure 18c. As a result of these errors, the image size of the single channel ViSAR system is limited to 40 m.

After applying the MCRA, azimuth ambiguities are suppressed, as shown in Figure 19. The unambiguous azimuth frequency of Scatterer E, which is measured as 751.3 Hz, is reconstructed correctly by the MCRA, as shown in Figure 19c. The other peaks in Figure 19c include the sidelobe of scatterer A, the sidelobe of scatterer C, and residual azimuth ambiguities due to mismatch of the azimuth reconstruction model. No windows are applied for sidelobe reduction for clear visualization the sidelobes.

The SAR video frame is shown in Figure 20. The video frame is 80 m in the down-range and cross-range, which is two times wider than the single channel system. As both the frame rate and image size are doubled, the azimuth frequency bandwidth is four times bigger than in the single channel case, as suggested by Equation (5).

s Figure 21 and Figure 22 show the SAR video frames before and after image rotation from 20° to 70°, with a 10° step in aspect angle, in order to recognize the difference between the SAR video frames. Only the values above −60 dB from the peak level are plotted. As shown in Figure 21, stationary targets appear to rotate, since the aspect angle changes continuously while the radar moves on a circular path.

Image rotation is implemented using Equation (55). As shown in Figure 22, when viewed successively, stationary targets appear fixed after image rotation to CDU, even though the aspect angle changes continuously.

In this case, the frame rate of the SAR video is calculated from Equation (4) as 2.005 Hz when v = 40 m/s, ${\rho }_a$ = 0.08 m, $R_a$ = 1000 m, and $f_c$ = 94 GHz. This frame rate is two times higher than the single channel system, with v = 20 m/s. Note that the platform velocity in the single channel system is limited to 20 m/s, due to the maximum Doppler frequency limitation dictated by Equation (5). In summary, the simulations show improved performance of the proposed MIMO ViSAR system measured by the frame rate and image size of the SAR video, which are two times higher than observed with a single channel system.

5. Conclusions

A novel MIMO ViSAR system and signal processing method were presented. This paper described theoretical aspects of ViSAR in terms of two important parameters: frame rate and image size. A MIMO signal model was selected for the proposed system, assuming broadside antenna beam orientation, and a collocated antenna configuration. The signal processing procedures for generating SAR video were then proposed.

The proposed system was able to overcome frame rate and image size limitations caused by azimuth ambiguities, using two notable advanced techniques: the MCRA, which is a multi-channel azimuth processing technique, and MIMO technology. The MCRA is used to increase the Doppler bandwidth by suppressing the azimuth ambiguities in multiple azimuth channels. MIMO technology was used to increase the equivalent number of receiving channels, by forming a virtual array using BFD FMCW as the orthogonal waveform.

The signal model and the signal processing method took into consideration Doppler compensation, required for mitigating effects caused by continuous antenna motion in FMCW-based SAR systems. Since the model used is based on a MIMO signal, it is easy to understand the relationship between beamsteering techniques for Tx and Rx, and multi-channel azimuth processing techniques.

Simulation results showed that the proposed MIMO ViSAR system and signal processing method improved performance, as measured by the frame rate and image size of the SAR video. Further research can be easily extended to multi-mode operation of ViSAR systems with MIMO technology, for example, InSAR and PolSAR.