Effect of Solar-Cloud-Satellite Geometry on Land Surface Shortwave Radiation Derived from Remotely Sensed Data
Abstract
:1. Introduction
2. Satellite Datasets
3. Methods
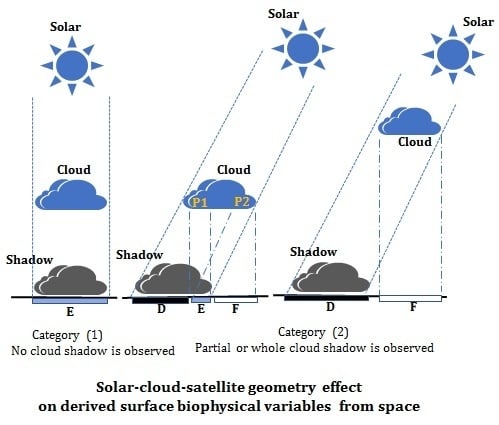
3.1. Determination of Orthographic Positions of Clouds and Their Shadows
3.2. Estimation of Land Surface Shortwave Downward Radiation (SWDR)
3.3. Solar-Cloud-Sensor Geometry Effect Correction
4. Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lv, H.; Wang, Y.; Shen, Y. An empirical and radiative transfer model based algorithm to remove thin clouds in visible bands. Remote Sens. Environ. 2016, 179, 183–195. [Google Scholar] [CrossRef]
- Menaka, E.; Kumar, S.; Bharathi, M. Cloud removal using efficient cloud detection and removal algorithm for high-resolution satellite imagery. J. Comput. Appl. Technol. 2015, 51, 54–61. [Google Scholar] [CrossRef]
- Eckardt, R.; Berger, C.; Thiel, C.; Schmullius, C. Removal of Optically Thick Clouds from Multi-Spectral Satellite Images Using Multi-Frequency SAR Data. Remote Sens. 2013, 5, 2973–3006. [Google Scholar] [CrossRef]
- Paudel, K.P.; Andersen, P. Monitoring snow cover variability in an agropastoral area in the Trans Himalayan region of Nepal using MODIS data with improved cloud removal methodology. Remote Sens. Environ. 2011, 115, 1234–1246. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Huang, H.; Schmit, T.J.; Wu, X.; Menzel, W.; Gurka, J.J. Optimal cloud-clearing for AIRS radiances using MODIS. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1266–1278. [Google Scholar]
- Gafurov, A.; Bardossy, A. Cloud removal methodology from MODIS snow cover product. Hydrol. Earth Syst. Sci. 2009, 13, 1361–1373. [Google Scholar] [CrossRef]
- Tseng, D.; Tseng, H.; Chien, C. Automatic cloud removal from multi-temporal SPOT images. Appl. Math. Comput. 2008, 205, 584–600. [Google Scholar] [CrossRef]
- Díaz, F.; Montero, H.; Santana, D.; Montero, G.; Rodríguez, E.; Aguiar, L.M.; Oliver, A. Improving shadows detection for solar radiation numerical models. Appl. Math. Comput. 2017, in press. [Google Scholar]
- Schutgens, N.A.J.; Roebeling, R.A. Validating the validation: The influence of liquid water distribution in clouds on the intercomparison of satellite and surface observations. J. Atmos. Ocean. Technol. 2009, 26, 1457–1474. [Google Scholar] [CrossRef]
- Li, S.; Sun, D.; Yu, Y. Automatic cloud-shadow removal from flood/standing water maps using MSG/SEVIRI imagery. Int. J. Remote Sens. 2013, 34, 5487–5502. [Google Scholar] [CrossRef]
- Iwabuchi, H.; Hayasaka, T. Effects of cloud horizontal inhomogeneity on the optical thickness retrieved from moderate-resolution satellite data. J. Atmos. Sci. 2002, 59, 2227–2242. [Google Scholar] [CrossRef]
- O’Hirok, W.; Gautier, C. A three-dimensional radiative transfer model to investigate the solar radiation within a cloudy atmosphere. Part I: Spatial effects. J. Atmos. Sci. 1998, 55, 2162–2179. [Google Scholar] [CrossRef]
- Fu, Q.; Cribb, M.C.; Barker, H.W.; Krueger, H.W.; Grossman, A. Cloud geometry effects on atmospheric solar absorption. J. Atmos. Sci. 2000, 57, 1156–1168. [Google Scholar] [CrossRef]
- Várnai, T. Influence of three-dimensional radiative effects on the spatial distribution of shortwave cloud reflection. J. Atmos. Sci. 2000, 57, 216–229. [Google Scholar] [CrossRef]
- Barker, H.W.; Stephens, G.L.; Partain, P.T.; Bergman, J.W.; Bonnel, B.; Campana, K.; Edwards, J. Assessing 1D atmospheric solar radiative transfer models: Interpretation and handling of unresolved clouds. J. Clim. 2003, 16, 2676–2699. [Google Scholar] [CrossRef]
- Di Giuseppe, F.; Tompkins, A.M. Effect of spatial organization on solar radiative transfer in three-dimensional idealized stratocumulus cloud fields. J. Atmos. Sci. 2003, 60, 1774–1794. [Google Scholar] [CrossRef]
- Hogan, R.J.; Shonk, J.K. Incorporating the effects of 3D radiative transfer in the presence of clouds into two-stream multilayer radiation schemes. J. Atmos. Sci. 2013, 70, 708–724. [Google Scholar] [CrossRef]
- Posselt, R.; Mueller, R.W.; Stöckli, R.; Trentmann, J. Remote sensing of solar surface radiation for climate monitoring—The CM-SAF retrieval in international comparison. Remote Sens. Environ. 2012, 118, 186–198. [Google Scholar] [CrossRef]
- The HelioMont Surface Solar Radiation Processing. Available online: https://www.gr.ch/DE/institutionen/verwaltung/dvs/are/Documents/heliomont_scientific_report.pdf (accessed on 11 May 2017).
- Yan, G.; Wang, T.; Jiao, Z.; Mu, X.; Zhao, J.; Chen, L. Topographic radiation modeling and spatial scaling of clear-sky land surface longwave radiation over rugged terrain. Remote Sens. Environ. 2016, 172, 15–27. [Google Scholar] [CrossRef]
- Wang, T.; Yan, G.; Chen, L. Consistent retrieval methods to estimate land surface shortwave and longwave radiative flux components under clear-sky conditions. Remote Sens. Environ. 2012, 124, 61–71. [Google Scholar] [CrossRef]
- Bisht, G.; Bras, R.L. Estimation of net radiation from the MODIS data under all sky conditions: Southern Great Plains case study. Remote Sens. Environ. 2010, 114, 1522–1534. [Google Scholar] [CrossRef]
- Kim, H.Y.; Liang, S. Development of a hybrid method for estimating land surface shortwave net radiation from MODIS data. Remote Sens. Environ. 2010, 114, 2393–2402. [Google Scholar] [CrossRef]
- Gupta, S.K.; Kratz, D.P.; Stackhouse, P.W., Jr.; Wilber, A.C.; Zhang, T.; Sothcott, V.E. Improvement of surface longwave flux algorithms used in CERES processing. J. Appl. Meteorol. Climatol. 2010, 49, 1579–1589. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S. Estimation of high-spatial resolution clear-sky longwave downward and net radiation over land surfaces from MODIS data. Remote Sens. Environ. 2009, 113, 745–754. [Google Scholar] [CrossRef]
- Zhou, Y.; Kratz, D.P.; Wilber, A.C.; Gupta, S.K.; Cess, R.D. An improved algorithm for retrieving surface downwelling longwave radiation from satellite measurements. J. Geophys. Res. 2007, 112, 1–13. [Google Scholar] [CrossRef]
- Tang, B.; Li, Z.; Zhang, R. A direct method for estimating net surface shortwave radiation from MODIS data. Remote Sens. Environ. 2006, 103, 115–126. [Google Scholar]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using MODIS data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Zhou, Y.P.; Cess, R.D. Algorithm development strategies for retrieving the downward longwave flux at the Earth’s surface. J. Geophys. Res. 2001, 106, 12477–12488. [Google Scholar] [CrossRef]
- Gupta, S.K. A parameterization for longwave surface radiation from Sun-synchronous satellite data. J. Clim. 1998, 2, 305–320. [Google Scholar] [CrossRef]
- Masuoka, E.; Fleig, A.J.; Wolfe, R.E.; Patt, F.S. Key characteristics of MODIS data products. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1313–1323. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.; Defries, R.S.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS land data processing and product status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, S.; Zhou, G.; Wu, H.; Zhao, X. Generating Global LAnd Surface Satellite incident shortwave radiation and photosynthetically active radiation products from multiple satellite data. Remote Sens. Environ. 2014, 152, 318–332. [Google Scholar] [CrossRef]
- Zheng, T.; Liang, S.; Wang, K. Estimation of Incident Photosynthetically Active Radiation from GOES Visible Imagery. J. Appl. Meteorol. Climatol. 2008, 47, 853–868. [Google Scholar] [CrossRef]
- Liang, S.; Zheng, T.; Liu, R.; Fang, H.; Tsay, S.C.; Running, S. Mapping incident Photosynthetically Active Radiation (PAR) from MODIS Data. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Li, Z.; Leighton, H.G.; Masuda, K.; Takashima, T. Estimation of SW flux absorbed at the surface from TOA reflected flux. J. Clim. 1993, 6, 317–330. [Google Scholar] [CrossRef]
- Frouin, R.; Chertock, B. A technique for global monitoring of net solar irradiance at the ocean surface. Part I: Model. J. Appl. Meteorol. 2010, 31, 943. [Google Scholar] [CrossRef]
- Dedieu, G.; Deschamps, P.Y.; Kerr, Y.H. Satellite estimation of solar irradiance at the surface of the earth and of surface albedo using a physical model applied to metcosat data. J. Appl. Meteorol. 1986, 26, 79–87. [Google Scholar] [CrossRef]
- Frouin, R.; Murakami, H. Estimating photosynthetically available radiation at the ocean surface from adeos-ii global imager data. J. Oceanogr. 2007, 63, 493–503. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo I: Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Available online: ftp://ladsweb.modaps.eosdis.nasa.gov/allData/6/MOD021KM/2010/033/ (accessed on 11 May 2017).





© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Shi, J.; Husi, L.; Zhao, T.; Ji, D.; Xiong, C.; Gao, B. Effect of Solar-Cloud-Satellite Geometry on Land Surface Shortwave Radiation Derived from Remotely Sensed Data. Remote Sens. 2017, 9, 690. https://doi.org/10.3390/rs9070690
Wang T, Shi J, Husi L, Zhao T, Ji D, Xiong C, Gao B. Effect of Solar-Cloud-Satellite Geometry on Land Surface Shortwave Radiation Derived from Remotely Sensed Data. Remote Sensing. 2017; 9(7):690. https://doi.org/10.3390/rs9070690
Chicago/Turabian StyleWang, Tianxing, Jiancheng Shi, Letu Husi, Tianjie Zhao, Dabin Ji, Chuan Xiong, and Bo Gao. 2017. "Effect of Solar-Cloud-Satellite Geometry on Land Surface Shortwave Radiation Derived from Remotely Sensed Data" Remote Sensing 9, no. 7: 690. https://doi.org/10.3390/rs9070690
APA StyleWang, T., Shi, J., Husi, L., Zhao, T., Ji, D., Xiong, C., & Gao, B. (2017). Effect of Solar-Cloud-Satellite Geometry on Land Surface Shortwave Radiation Derived from Remotely Sensed Data. Remote Sensing, 9(7), 690. https://doi.org/10.3390/rs9070690