Retrieval of Biophysical Crop Variables from Multi-Angular Canopy Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area & Sampling Layout
2.2. In Situ Measurements
2.2.1. Spectral Data
2.2.2. Biophysical Variables
2.3. Radiative Transfer Modelling
2.4. Step-Wise Inversion of the LUT
3. Results
3.1. Impact of the Observer Zenith on Reflectance Spectra
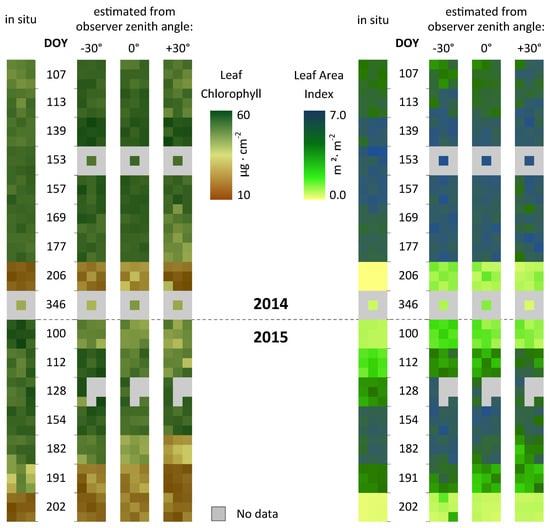
3.2. Impact of the Observer Zenith on the Retrieval of Crop Parameters
3.3. Improved Look-Up-Table Inversions
4. Discussion
5. Conclusions
- Effects of anisotropy are strongest for early phenological stages and backscatter observations;
- LAI is best estimated from near-nadir observations;
- Optimal results for a retrieval of leaf chlorophyll content is achieved for an observer zenith angle opposite to the sun (forward scatter);
- For both variables (LAI and LCC) feasible results are obtained for all considered EnMAP geometrical constellations.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Atzberger, C.; Richter, K. Spatially constrained inversion of radiative transfer models for improved LAI mapping from future Sentinel-2 imagery. Remote Sens. Environ. 2012, 120, 208–218. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; García-Haro, F.J.; Camps-Valls, G.; Grau-Muedra, G.; Nutini, F.; Crema, A.; Boschetti, M. Multitemporal and multiresolution leaf area index retrieval for operational local rice crop monitoring. Remote Sens. Environ. 2016, 187, 102–118. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Leonenko, G.; Alonso, L.; Moreno, J. Optimizing lut-based rtm inversion for semiautomatic mapping of crop biophysical parameters from Sentinel-2 and-3 data: Role of cost functions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 257–269. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods—A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Bontemps, S.; Arias, M.; Cara, C.; Dedieu, G.; Guzzonato, E.; Hagolle, O.; Inglada, J.; Matton, N.; Morin, D.; Popescu, R. Building a data set over 12 globally distributed sites to support the development of agriculture monitoring applications with Sentinel-2. Remote Sens. 2015, 7, 16062–16090. [Google Scholar] [CrossRef]
- Locherer, M.; Hank, T.; Danner, M.; Mauser, W. Retrieval of seasonal leaf area index from simulated enmap data through optimized lut-based inversion of the prosail model. Remote Sens. 2015, 7, 10321–10346. [Google Scholar] [CrossRef]
- Atzberger, C.; Jarmer, T.; Schlerf, M.; Kötz, B.; Werner, W. Retrieval of wheat bio-physical attributes from hyperspectral data and sailh+ prospect radiative transfer model. In Proceedings of the 3rd EARSeL Workshop on Imaging Spectroscopy, Herrsching, Germany, 13–16 May 2003; pp. 473–482. [Google Scholar]
- Duan, S.-B.; Li, Z.-L.; Wu, H.; Tang, B.-H.; Ma, L.; Zhao, E.; Li, C. Inversion of the prosail model to estimate leaf area index of maize, potato, and sunflower fields from unmanned aerial vehicle hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 12–20. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Camacho, F. Optimal modalities for radiative transfer-neural network estimation of canopy biophysical characteristics: Evaluation over an agricultural area with chris/proba observations. Remote Sens. Environ. 2011, 115, 415–426. [Google Scholar] [CrossRef]
- Honkavaara, E.; Kaivosoja, J.; Mäkynen, J.; Pellikka, I.; Pesonen, L.; Saari, H.; Salo, H.; Hakala, T.; Marklelin, L.; Rosnell, T. Hyperspectral reflectance signatures and point clouds for precision agriculture by light weight uav imaging system. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-7, 353–358. [Google Scholar] [CrossRef]
- Burkart, A.; Aasen, H.; Alonso, L.; Menz, G.; Bareth, G.; Rascher, U. Angular dependency of hyperspectral measurements over wheat characterized by a novel uav based goniometer. Remote Sens. 2015, 7, 725–746. [Google Scholar] [CrossRef]
- Richter, K.; Atzberger, C.; Vuolo, F.; Weihs, P.; d’Urso, G. Experimental assessment of the Sentinel-2 band setting for rtm-based LAI retrieval of sugar beet and maize. Can. J. Remote Sens. 2009, 35, 230–247. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of spectral-temporal response surfaces by combining multispectral satellite and hyperspectral uav imagery for precision agriculture applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Yang, C.; Everitt, J.H.; Du, Q.; Luo, B.; Chanussot, J. Using high-resolution airborne and satellite imagery to assess crop growth and yield variability for precision agriculture. Proc. IEEE 2013, 101, 582–592. [Google Scholar] [CrossRef]
- Schueller, J.K. A review and integrating analysis of spatially-variable control of crop production. Fertil. Res. 1992, 33, 1–34. [Google Scholar] [CrossRef]
- Baret, F.; Buis, S. Estimating canopy characteristics from remote sensing observations. Review of methods and associated problems. Adv. Land Remote Sens. Syst. Model. Invers. Appl. 2008, 173–201. [Google Scholar] [CrossRef]
- Danner, M.; Hank, T.; Mauser, W. Comparing the potential of the Sentinel-2 msi and the future enmap hsi for the retrieval of winter wheat crop parameters in southern germany. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; p. 93. [Google Scholar]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The sail model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Goel, N.S. Models of vegetation canopy reflectance and their use in estimation of biophysical parameters from reflectance data. Remote Sens. Rev. 1988, 4, 1–212. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. Prospect: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. Prospect+ sail models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Kimes, D.; Knyazikhin, Y.; Privette, J.; Abuelgasim, A.; Gao, F. Inversion methods for physically-based models. Remote Sens. Rev. 2000, 18, 381–439. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Flasse, S.; Verdebout, J.; Schmuck, G. Comparison of several optimization methods to extract canopy biophysical parameters-application to caesar data. In Proceedings of the 6th International Symposium on Physical Measurements and Signatures in Remote Sensing, Val D’Isere, France, 17–21 January 1994; pp. 291–298. [Google Scholar]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Mace, D.; Pragnere, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of canopy biophysical variables from bidirectional reflectance: Using prior information to solve the ill-posed inverse problem. Remote Sens. Environ. 2003, 84, 1–15. [Google Scholar] [CrossRef]
- Liang, S. Recent developments in estimating land surface biogeophysical variables from optical remote sensing. Prog. Phys. Geogr. 2007, 31, 501–516. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Myneni, R.; Pragnère, A.; Knyazikhin, Y. Investigation of a model inversion technique to estimate canopy biophysical variables from spectral and directional reflectance data. Agronomie 2000, 20, 3–22. [Google Scholar] [CrossRef]
- Baret, F.; Knyazikhin, Y.; Weiss, M.; Pragnère, A.; Myneni, R. Overview of retrieval techniques for LAI and fapar. In Proceedings of the ALPS99 Workshop, Meribel, France, 18–22 January 1999. [Google Scholar]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C. The enmap spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Foerster, S.; Brosinsky, A.; Wulf, H.; Bochow, M.; Boesche, N.; Brell, M.; Buddenbaum, H.; Chabrillat, S.; et al. Enmap Science Plan; GFZ: Potsdam, Germany, 2016. [Google Scholar]
- Loizzo, R.; Ananasso, C.; Guarini, R.; Lopinto, E.; Candela, L.; Pisani, A. The prisma hyperspectral mission. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; p. 415. [Google Scholar]
- Storch, T.; Bachmann, M.; Eberle, S.; Habermeyer, M.; Makasy, C.; de Miguel, A.; Mühle, H.; Müller, R. Enmap ground segment design: An overview and its hyperspectral image processing chain. In Earth Observation of Global Changes; Springer: Berlin, Germany, 2013; pp. 49–62. [Google Scholar]
- Stuffler, T.; Hofer, S.; Leipold, M.; Förster, K.; Sang, B.; Schubert, J.; Penné, B.; Kaufmann, H.; Müller, A.; Chlebek, C. Enmap—Space segment—Instrument and mission parameters. In Proceedings of the EARSeL SIG-IS Workshop, Tel Aviv, Israel, 16–19 March 2009. [Google Scholar]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 4. The extinction coefficient and the opposition effect. Icarus 1986, 67, 264–280. [Google Scholar] [CrossRef]
- Kaufmann, H.; Hill, J.; Hostert, P.; Krasemann, H.; Mauser, W.; Muller, A. Science Plan of the Environmental Mapping and Analysis Program (ENMAP); Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2012. [Google Scholar]
- Segl, K.; Guanter, L.; Rogass, C.; Kuester, T.; Roessner, S.; Kaufmann, H.; Sang, B.; Mogulsky, V.; Hofer, S. Eetes—The enmap end-to-end simulation tool. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 522–530. [Google Scholar] [CrossRef]
- Baret, F.; Clevers, J.; Steven, M. The robustness of canopy gap fraction estimates from red and near-infrared reflectances: A comparison of approaches. Remote Sens. Environ. 1995, 54, 141–151. [Google Scholar] [CrossRef]
- Sandmeier, S.; Müller, C.; Hosgood, B.; Andreoli, G. Physical mechanisms in hyperspectral brdf data of grass and watercress. Remote Sens. Environ. 1998, 66, 222–233. [Google Scholar] [CrossRef]
- Wang, L.; Dong, T.; Zhang, G.; Niu, Z. LAI retrieval using prosail model and optimal angle combination of multi-angular data in wheat. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1730–1736. [Google Scholar] [CrossRef]
- Hilker, T.; Gitelson, A.; Coops, N.C.; Hall, F.G.; Black, T.A. Tracking plant physiological properties from multi-angular tower-based remote sensing. Oecologia 2011, 165, 865–876. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, R.; Sahoo, R.N.; Sehgal, V.K.; Tomar, R.K.; Chakraborty, D.; Nagarajan, S. Inversion of prosail model for retrieval of plant biophysical parameters. J. Indian Soc. Remote Sens. 2012, 40, 19–28. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Coupled soil-leaf-canopy and atmosphere radiative transfer modeling to simulate hyperspectral multi-angular surface reflectance and toa radiance data. Remote Sens. Environ. 2007, 109, 166–182. [Google Scholar] [CrossRef]
- Vuolo, F.; Dini, L.; D’urso, G. Retrieval of leaf area index from chris/proba data: An analysis of the directional and spectral information content. Int. J. Remote Sens. 2008, 29, 5063–5072. [Google Scholar] [CrossRef]
- Gratani, L.; Ghia, E. Changes in morphological and physiological traits during leaf expansion of arbutus unedo. Environ. Exp. Bot. 2002, 48, 51–60. [Google Scholar] [CrossRef]
- Goel, N.S.; Strebel, D.E. Simple beta distribution representation of leaf orientation in vegetation canopies. Agron. J. 1984, 76, 800–802. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K. [34] chlorophylls and carotenoids: Pigments of photosynthetic biomembranes. Methods Enzymol. 1987, 148, 350–382. [Google Scholar]
- Verhoef, W.; Bach, H. Simulation of hyperspectral and directional radiance images using coupled biophysical and atmospheric radiative transfer models. Remote Sens. Environ. 2003, 87, 23–41. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Matkan, A.A.; Ahangar, A.D. Inversion of a radiative transfer model for estimation of rice canopy chlorophyll content using a lookup-table approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1222–1230. [Google Scholar] [CrossRef]
- Wainwright, J.; Mulligan, M. Environmental Modelling: Finding Simplicity in Complexity; John Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
- Richter, K.; Atzberger, C.; Hank, T.B.; Mauser, W. Derivation of biophysical variables from earth observation data: Validation and statistical measures. J. Appl. Remote Sens. 2012, 6. [Google Scholar] [CrossRef]
- Dorigo, W.A. Improving the robustness of cotton status characterisation by radiative transfer model inversion of multi-angular chris/proba data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 18–29. [Google Scholar] [CrossRef]
- Asner, G.P.; Wessman, C.A.; Schimel, D.S.; Archer, S. Variability in leaf and litter optical properties: Implications for brdf model inversions using avhrr, modis, and misr. Remote Sens. Environ. 1998, 63, 243–257. [Google Scholar] [CrossRef]
- Sehgal, V.K.; Chakraborty, D.; Sahoo, R.N. Inversion of radiative transfer model for retrieval of wheat biophysical parameters from broadband reflectance measurements. Inf. Process. Agric. 2016, 3, 107–118. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.; Moreno, J. Artmo’s global sensitivity analysis (gsa) toolbox to quantify driving variables of leaf and canopy radiative transfer models. EARSeL eProc. 2015, 14, 1–11. [Google Scholar]
- Jacquemoud, S. Inversion of the prospect+ sail canopy reflectance model from aviris equivalent spectra: Theoretical study. Remote Sens. Environ. 1993, 44, 281–292. [Google Scholar] [CrossRef]
- Féret, J.-B.; Gitelson, A.; Noble, S.; Jacquemoud, S. Prospect-d: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C. Vegetation structure retrieval in beech and spruce forests using spectrodirectional satellite data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 8–17. [Google Scholar] [CrossRef]









| Date | Spectral Nadir | Spectral Angles | Crop Variables | Date | Spectral Nadir | Spectral Angles | Crop Variables |
|---|---|---|---|---|---|---|---|
| 17 April 2014 | √ | √ | √ | 28 November 2014 | √ | ||
| 23 April 2014 | √ | √ | √ | 12 December 2014 | √ | √ | √ |
| 30 April 2014 | √ | 19 March 2015 | √ | √ | |||
| 6 May 2014 | √ | 10 April 2015 | √ | √ | √ | ||
| 14 May 2014 | √ | 22 April 2015 | √ | √ | √ | ||
| 9 May 2014 | √ | √ | √ | 5 May 2015 | √ | ||
| 26 May 2014 | √ | 8 May 2015 | √ | √ | √ | ||
| 2 June 2014 | √ | √ | √ | 3 June 2015 | √ | √ | √ |
| 6 June 2014 | √ | √ | √ | 12 June 2015 | √ | √ | |
| 18 June 2014 | √ | √ | √ | 1 July 2015 | √ | √ | √ |
| 26 June 2014 | √ | √ | √ | 10 July 2015 | √ | √ | √ |
| 3 July 2014 | √ | √ | 16 July 2015 | √ | √ | ||
| 17 July 2014 | √ | √ | 21 July 2015 | √ | √ | √ | |
| 25 July 2014 | √ | √ | √ | ||||
| Total observation number | 10 | 8 | 14 | Total observation number | 11 | 8 | 1 |
| Model | Parameter | Description | Unit | Min | Max | |
|---|---|---|---|---|---|---|
| PROSPECT | N | Leaf structure parameter | - | 1.0 | 2.5 | |
| LCC | Leaf Chlorophylla+b content | mg cm−2 | 0.0 | 80 | ||
| LCarC | Leaf Carotenoids content | μg cm−2 | 0.0 | 20 | ||
| EWT | Leaf Equivalent Water content | cm | 0.001 | 0.05 | ||
| LMA | Leaf Mass per Area | g cm−2 | 0.001 | 0.02 | ||
| Cbr | Fraction of brown leaves | - | 0.0 | 1.0 | ||
| SAIL | LAI | Leaf Area Index | m² m−2 | 0.0 | 8.0 | |
| ALIA | Average Leaf Inclination Angle | deg | 20 | 90 | ||
| Hspot | Hot Spot size parameter | - | 0.01 | 0.5 | ||
| Skyl | Ratio of diffuse and total incident radiation | - | 0.1 | 0.1 | ||
| γ | Soil Brightness Parameter | - | 0.0 | 1.0 | ||
| Model | Parameter | Description | Unit | Min | Max | Divisions |
| SAIL | SZA | Sun Zenith Angle | deg | 30 | 55 | 6 |
| OZA | Observer Zenith Angle | deg | −30 | 30 | 3 | |
| rAA | relative Azimuth Angle | deg | 0 | 65 | 14 | |
| OZA | RMSE Cost Function | MAE Cost Function | ||||||
|---|---|---|---|---|---|---|---|---|
| LAI | LCC | LAI | LCC | |||||
| (deg) | Slope | rRMSE | Slope | rRMSE | Slope | rRMSE | Slope | rRMSE |
| −30 | 0.81 | 0.27 | 0.95 | 0.20 | 0.84 | 0.24 | 0.82 | 0.22 |
| 0 | 0.94 | 0.19 | 0.87 | 0.24 | 0.92 | 0.18 | 0.89 | 0.26 |
| +30 | 0.83 | 0.25 | 0.94 | 0.27 | 0.82 | 0.27 | 0.79 | 0.28 |
| OZA | Season 2014 | Season 2014/2015 | ||
|---|---|---|---|---|
| LAI | LCC | LAI | LCC | |
| (deg) | (m² m−2) | (μg cm−2) | (m² m−2) | (μg cm−2) |
| −30° | 0.62 | 8.43 | 0.99 | 7.44 |
| 0° | 0.47 | 11.86 | 0.82 | 7.17 |
| +30° | 0.59 | 7.38 | 1.08 | 11.22 |
| Noise Level | Additive Noise | Inverse Multiplicative Noise | ||||||
|---|---|---|---|---|---|---|---|---|
| LAI | LCC | LAI | LCC | |||||
| σ (%) | Slope | rRMSE | Slope | rRMSE | Slope | rRMSE | Slope | rRMSE |
| 0.0 | 0.89 | 0.19 | 1.50 | 0.34 | 0.89 | 0.19 | 1.50 | 0.34 |
| 0.1 | 0.89 | 0.19 | 1.49 | 0.33 | 0.89 | 0.19 | 1.33 | 0.30 |
| 1.0 | 0.89 | 0.20 | 1.40 | 0.29 | 0.89 | 0.19 | 1.33 | 0.30 |
| 2.0 | 0.88 | 0.22 | 1.30 | 0.29 | 0.89 | 0.19 | 1.34 | 0.30 |
| 5.0 | 0.80 | 0.29 | 1.24 | 0.28 | 0.90 | 0.19 | 1.32 | 0.30 |
| 10.0 | 0.64 | 0.38 | 1.68 | 0.31 | 0.88 | 0.20 | 1.27 | 0.27 |
| Number of Best Fits | RMSE Cost Function | MAE Cost Function | ||||||
|---|---|---|---|---|---|---|---|---|
| LAI | LCC | LAI | LCC | |||||
| Slope | rRMSE | Slope | rRMSE | Slope | rRMSE | Slope | rRMSE | |
| 1 | 0.88 | 0.28 | 1.61 | 0.44 | 0.88 | 0.28 | 1.55 | 0.42 |
| 50 | 0.94 | 0.19 | 1.44 | 0.32 | 0.93 | 0.18 | 1.36 | 0.32 |
| 100 | 0.89 | 0.19 | 1.30 | 0.29 | 0.92 | 0.18 | 1.18 | 0.28 |
| 200 | 0.90 | 0.20 | 1.26 | 0.28 | 0.89 | 0.18 | 1.13 | 0.28 |
| 500 | 0.86 | 0.21 | 1.03 | 0.26 | 0.87 | 0.20 | 0.89 | 0.26 |
| 1000 | 0.83 | 0.22 | 0.87 | 0.24 | 0.84 | 0.20 | 0.77 | 0.26 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Retrieval of Biophysical Crop Variables from Multi-Angular Canopy Spectroscopy. Remote Sens. 2017, 9, 726. https://doi.org/10.3390/rs9070726
Danner M, Berger K, Wocher M, Mauser W, Hank T. Retrieval of Biophysical Crop Variables from Multi-Angular Canopy Spectroscopy. Remote Sensing. 2017; 9(7):726. https://doi.org/10.3390/rs9070726
Chicago/Turabian StyleDanner, Martin, Katja Berger, Matthias Wocher, Wolfram Mauser, and Tobias Hank. 2017. "Retrieval of Biophysical Crop Variables from Multi-Angular Canopy Spectroscopy" Remote Sensing 9, no. 7: 726. https://doi.org/10.3390/rs9070726
APA StyleDanner, M., Berger, K., Wocher, M., Mauser, W., & Hank, T. (2017). Retrieval of Biophysical Crop Variables from Multi-Angular Canopy Spectroscopy. Remote Sensing, 9(7), 726. https://doi.org/10.3390/rs9070726