Impact Analysis of Climate Change on Snow over a Complex Mountainous Region Using Weather Research and Forecast Model (WRF) Simulation and Moderate Resolution Imaging Spectroradiometer Data (MODIS)-Terra Fractional Snow Cover Products
Abstract
:1. Introduction
2. Materials and Methods
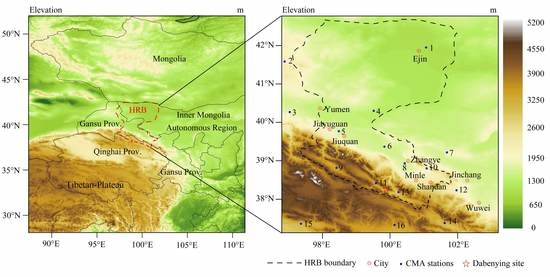
2.1. Research Region
2.2. Precipitation from the China Meteorological Administration Station Data
2.3. Snow-Related Variables Simulated by WRF-ARW and Model Configuration
2.4. MODIS-Terra FSC Remote Sensing Product
2.5. Empirical Orthogonal Function Analysis
2.6. Mann-Kendall/Theil-Sen Trend Analysis
3. Results
3.1. Spatial Patterns
3.2. Temporal Pattern
3.3. Long-Term Observational Snowfall
3.4. EOF Analysis
3.5. Mann-Kendall/Theil-Sen Trend Analysis
4. Discussion
4.1. Response of Snow-Related Variables to Climate Change
4.2. The Importance of High Spatial Resolution Data in the Evaluation of the Impact of Climate Change on Snow
4.3. Mutual Proofs for Remote Sensing Products and WRF Simulation
4.4. MODIS-Terra FSC Remote Sensing Product
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. (Eds.) IPCC Climate Change 2013: The Physical Science Basis. In Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Bell, V.A.; Kay, A.L.; Davies, H.N.; Jones, R.G. An assessment of the possible impacts of climate change on snow and peak river flows across Britain. Clim. Chang. 2016, 136, 539–553. [Google Scholar] [CrossRef]
- Rasmussen, R.; Liu, C.; Ikeda, K.; Gochis, D.; Yates, D.; Chen, F.; Tewari, M.; Barlage, M.; Dudhia, J.; Yu, W.; et al. High-resolution coupled climate runoff simulations of seasonal snowfall over Colorado: A process study of current and warmer climate. J. Clim. 2011, 24, 3015–3048. [Google Scholar] [CrossRef]
- Burnett, A.W.; Kirby, M.E.; Mullins, H.T.; Patterson, W.P. Increasing great lake–effect snowfall during the twentieth century: A regional response to global warming? J. Clim. 2003, 16, 3535–3542. [Google Scholar] [CrossRef]
- Wright, D.M.; Posselt, D.J.; Steiner, A.L. Sensitivity of lake-effect snowfall to lake ice cover and temperature in the great lakes region. Mon. Weather Rev. 2013, 141, 670–689. [Google Scholar] [CrossRef]
- Zhang, R.-N.; Zhang, R.-H.; Zuo, Z. Characteristics and differences of multi-snow data in winter over China. Clim. Environ. Res. 2014, 19, 572–586. (In Chinese) [Google Scholar]
- Dai, L.; Che, T. Spatiotemporal variability in snow cover from 1987 to 2011 in northern China. J. Appl. Remote Sens. 2014, 8, 1–16. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.D.; Jin, H.J.; Kang, E.S.; Che, T.; Jin, R.; Wu, L.Z.; Nan, Z.T.; Wang, J.; Shen, Y. Cryospheric change in China. Glob. Planet. Chang. 2008, 62, 210–218. [Google Scholar] [CrossRef]
- Zang, H.; Zhou, Z. Regional snow depth increment time series with its variation in the Qinghai-Tibet Plateau. Meteorol. Mon. 2009, 35, 77–81. (In Chinese) [Google Scholar]
- Huang, X.; Deng, J.; Wang, W.; Feng, Q.; Liang, T. Impact of climate and elevation on snow cover using integrated remote sensing snow products in Tibetan Plateau. Remote Sens. Environ. 2017, 190, 274–288. [Google Scholar] [CrossRef]
- Dang, S.; Liu, C.; Wang, Z.; Wu, M. Spaio-temporal distribution characteristics of snow cover in the upper reaches of Heihe River Basin over the past 10 years and the variation trend. Resour. Sci. 2012, 34, 1574–1581. [Google Scholar]
- Wang, H.; Yu, E.; Yang, S. An exceptionally heavy snowfall in Northeast China: Large-scale circulation anomalies and hindcast of the NCAR WRF model. Meteorol. Atmos. Phys. 2011, 113, 11–25. [Google Scholar] [CrossRef]
- Yu, E.T. High-resolution seasonal snowfall simulation over Northeast China. Chin. Sci. Bull. 2013, 58, 1–8. [Google Scholar] [CrossRef]
- Lee, J.G.; Kim, Y.J. A numerical simulation study using WRF of a heavy snowfall event in the Yeongdong coastal area in relation to the northeasterly. Atmosphere 2008, 18, 339–354, (In Korean with English abstract). [Google Scholar]
- Robinson, D.A.; Dewey, K.F. Recent secular variations in the extent of Northern Hemisphere snow cover. Geophys. Res. Lett. 1990, 17, 1557–1560. [Google Scholar] [CrossRef]
- Robinson, D.A.; Keimig, F.T.; Dewey, K.F. Recent Variations in Northern Hemisphere Snow Cover. In Proceedings of the 15th Annual Climate Diagnostics Workshop, Asheville, NC, USA, 29 October–2 November 1991; pp. 219–224. [Google Scholar]
- Gutzler, D.S.; Rosen, R.D. Interannual variability of wintertime snow cover across the Northern Hemisphere. J. Clim. 1992, 5, 1441–1447. [Google Scholar] [CrossRef]
- Arsenault, K.R.; Houser, P.R.; de Lannoy, G.J.M. Evaluation of the MODIS snow cover fraction product. Hydrol. Process. 2014, 28, 980–998. [Google Scholar] [CrossRef] [Green Version]
- Pu, Z.; Xu, L.; Salomonson, V.V. MODIS/Terra observed seansonal variations of snow cover over the Tibetan Plateau. Geophys. Res. Lett. 2007, 34, 137–161. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Liang, T. Evaluation of MODIS snow cover and cloud mask and its application in Northern Xinjiang, China. Remote Sens. Environ. 2008, 112, 1497–1513. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Qi, S.; Cai, Y. Mapping and assessment of degraded land in the Heihe River Basin, arid northwestern China. Sensors 2007, 7, 2565–2578. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, Y.; Li, S.; Wu, B. Downstream ecosystem responses to middle reach regulation of river discharge in the Heihe River Basin, China. Hydrol. Earth Syst. Sci. 2016, 20, 4469–4481. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Ren, L.L.; Skaggs, T.H.; Lü, H.S.; Yu, Z.B.; Wu, Y.Q.; Fang, X.Q. Simulation of populus euphratica root uptake of groundwater in an arid woodland of the Ejina Basin, China. Hydrol. Process. 2009, 23, 2460–2469. [Google Scholar] [CrossRef]
- Ding, B.; Yang, K.; Qin, J.; Wang, L.; Chen, Y.; He, X. The dependence of precipitation types on surface elevation and meteorological conditions and its parameterization. J. Hydrol. 2014, 513, 154–163. [Google Scholar] [CrossRef]
- China Meteorological Administration (CMA). Specifications for Surface Meteorological Observation Part 4: Observation of Weather Phenomenon (QX/T 48-2007); China Meteorological Press: Beijing, China, 2007; pp. 1–16.
- Chen, R.; Liu, J.; Kang, E.; Yang, Y.; Han, C.; Liu, Z.; Song, Y.; Qing, W.; Zhu, P. Precipitation measurement intercomparison in the Qilian Mountains, north-eastern Tibetan Plateau. Cryosphere 2015, 9, 1995–2008. [Google Scholar] [CrossRef]
- Chen, R.S.; Song, Y.X.; Kang, E.S.; Han, C.T.; Liu, J.F.; Yang, Y.; Qing, W.W.; Liu, Z.W. A cryosphere-hydrology observation system in a small alpine watershed in the Qilian Mountains of China and its meteorological gradient. Arct. Antarct. Alp. Res. 2014, 46, 505–523. [Google Scholar] [CrossRef]
- Michalakes, J.; Dudhia, J.; Gill, D. Design of a next-generation regional weather research and forecast model. In Towards Teracomputing, Proceeding of the Eighth ECMWF Workshop on the Use of Parallel Processors in Meteorology; World Scientific Publishing: Singapore, 1999; pp. 117–124. [Google Scholar]
- Michalakes, J.; Chen, S.; Dudhia, J.; Hart, L.; Klemp, J.B. Development of a next generation regional weather research and forecast model. In Developments in Teracomputing. Proceedings of the Ninth ECMWF Workshop on the Use of High Performance Computing in Meteorology; World Scientific Publishing: Singapore, 2001; pp. 269–276. [Google Scholar]
- Michalakes, J.; Dudhia, J.; Gill, D. The Weather Research and Forecast Model: Software Architecture and Performance. In Proceedings of the 11th ECMWF Workshop on the Use of High Performance Computing in Meteorology, Reading, UK, 25–29 October 2004; pp. 25–29. [Google Scholar]
- Michalakes, J.; Hacker, J.; Loft, R.; McCracken, M.O.; Snavely, A.; Wright, N.J.; Spelce, T.; Gorda, B.; Walkup, R. WRF nature run. J. Phys. Conf. Ser. 2008, 125, 12–22. [Google Scholar] [CrossRef]
- Laprise, R. The Euler equations of motion with hydrostatic pressure as an independent variable. Mon. Weather Rev. 1992, 120, 197–207. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational design of the basic dynamical processes of the UCLA general circulation model. In Methods in Computational Physics; Chang, J., Ed.; Academic Press: New York, NY, USA, 1977; Volume 17, pp. 173–265. [Google Scholar]
- Pan, X.; Li, X.; Cheng, G.; Li, H.; He, X. Development and evaluation of a river-basin-scale high spatio-temporal precipitation data set using the WRF model: A case study of the Heihe River Basin. Remote Sens. 2015, 7, 9230–9252. [Google Scholar] [CrossRef]
- Kessler, E. On the distribution and continuity of water substance in atmospheric circulation. Meteorol. Monogr. 1969, 32, 84. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef]
- Hong, S.Y.; Pan, H.L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. Development of methods for mapping global snow cover using moderate resolution imaging spectroradiometer data. Remote Sens. Environ. 1995, 54, 127–140. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; DiGirolamo, N.E.; Bayr, K.J. MODIS snow-cover products. Remote Sens. Environ. 2002, 83, 181–194. [Google Scholar] [CrossRef]
- Klein, A.G.; Hall, D.K.; Riggs, G.A. Improving snow-cover mapping in forests through the use of a canopy reflectance model. Hydrol. Process. 1998, 12, 1723–1744. [Google Scholar] [CrossRef]
- Hall, D.K.; Salomonson, V.V.; Riggs, G.A. MODIS/Terra Snow Cover Monthly L3 Global 0.05 deg CMG; Version 5; National Snow and Ice Data Center: Boulder, CO, USA, 2006. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences: An Introduction, 2nd ed.; Academic Press: New York, NY, USA, 1995; pp. 465–508. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Wang, X.; Yu, Q. Unbiasedness of the Theil–Sen estimator. J. Nonparametr. Stat. 2005, 17, 685–695. [Google Scholar] [CrossRef]
- Jishi, Z.; Ersi, K.; Yongchao, L.; Rensheng, C. Impact of climate change and variability on water resources in Heihe River Basin. J. Geogr. Sci. 2003, 13, 286–292. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, R.; Han, H.; Wang, X.; Si, J. Hydrological and water resources effects under climate change in Heihe River Basin. Resour. Sci. 2007, 1, 77–83. [Google Scholar]
- Wang, J.; Meng, J.J. Characteristics and tendencies of annual runoff variations in the Heihe River Basin during the past 60 years. Sci. Geogr. Sin. 2008, 28, 83–88. [Google Scholar]
- Lin, L.; Zhenyu, W.; Qingchun, W. Inflence of climatic change on flow over the upper reaches of Heihe River. Sci. Geogr. Sin. 2006, 26, 40–46. [Google Scholar]
- Zhang, A.; Zheng, C.; Wang, S.; Yao, Y. Analysis of streamflow variations in the Heihe River Basin, northwest China: Trends, abrupt changes, driving factors and ecological influences. J. Hydrol. Reg. Stud. 2015, 3, 106–124. [Google Scholar] [CrossRef]
- Wang, J.; Li, S. Effect of climatic change on snowmelt runoffs in mountainous regions of inland rivers in Northwestern China. Sci. China Ser. D 2006, 49, 881–888. [Google Scholar] [CrossRef]
- Cao, L.; Dou, Y. The spatial and temporal characteristics and forecasting method of precipitation in Heihe Field. Arid Meteorol. 2005, 23, 35–39. [Google Scholar]
- Ding, Y.; Ye, B.; Zhou, W. Temporal and spatial precipitation distribution in the Heihe catchment, northwest China, during the past 40 a. J. Glaciol. Geocryol. 1999, 21, 42–48. [Google Scholar]
- Lan, Y.C.; Kang, E.S.; Zhang, J.S.; Hu, X.L. Relationship between ENSO circle and air temperature, precipitation and runoff in the Qilian Mountain region in the past 50 years. Adv. Water Sci. 2002, 13, 141–145. [Google Scholar]
- Feser, F.; Rockel, B.; von Storch, H.; Winterfeldt, J.; Zahn, M. Regional climate models add value to global model data: A review and selected examples. Bull. Am. Meteorol. Soc. 2011, 92, 1181–1192. [Google Scholar] [CrossRef]
- Sylla, M.B.; Gaye, A.T.; Jenkins, G.S. On the fine-scale topography regulating changes in atmospheric hydrological cycle and extreme rainfall over West Africa in a regional climate model projections. Int. J. Geophys. 2012, 2012, 1–15. [Google Scholar] [CrossRef]
- Sylla, M.B.; Pal, J.S.; Wang, G.L.; Lawrence, P.J. Impact of land cover characterization on regional climate modeling over West Africa. Clim. Dyn. 2016, 46, 637–650. [Google Scholar] [CrossRef]









| Elevation (km) | <1.0 | (1.0, 1.5) | (1.5, 2.0) | (2.0, 2.5) | (2.5, 3.0) | (3.0, 3.5) | (3.5, 4.0) | (4.0, 4.5) | ≥4.5 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Precipitation | Probability | 0.00 | 0.26 | 0.94 | 0.96 | 0.96 | 0.56 | 0.77 | 0.73 | 0.92 |
| Trend (mm/year) | −0.10 | 0.14 | 3.142 | 11.02 | 14.01 | −5.23 | 9.00 | 7.13 | −15.12 | |
| Snowfall | Probability | 0.77 | 0.81 | 0.09 | 0.42 | 0.26 | 0.34 | 0.34 | 0.17 | 0.09 |
| Trend (mm/year) | −0.07 | −0.05 | 0.00 | 0.53 | 1.12 | 0.24 | 0.58 | 0.21 | −0.16 | |
| Snow water equivalent | Probability | 0.81 | 0.26 | 0.09 | 0.90 | 0.81 | 0.42 | 0.09 | 0.49 | 0.77 |
| Trend m-2/year) | −0.01 | 0.00 | 0.00 | 0.06 | 0.07 | −0.01 | 0.00 | −0.03 | −0.10 | |
| Snow depth | Probability | 0.87 | 0.81 | 0.00 | 068 | 0.68 | 0.09 | 0.56 | 0.87 | 0.99 |
| Trend (m/year) | −0.15 | −0.07 | 0.00 | 0.28 | 0.45 | 0.02 | −0.20 | −0.57 | −1.39 | |
| Fractional snow cover | Probability | 0.62 | 0.56 | 0.00 | 0.77 | 0.87 | 0.09 | 0.42 | 0.00 | 0.73 |
| Trend (%/year) | −0.06 | −0.13 | −0.01 | 0.25 | 0.25 | 0.05 | 0.11 | 0.03 | −0.68 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, X.; Li, X.; Cheng, G.; Chen, R.; Hsu, K. Impact Analysis of Climate Change on Snow over a Complex Mountainous Region Using Weather Research and Forecast Model (WRF) Simulation and Moderate Resolution Imaging Spectroradiometer Data (MODIS)-Terra Fractional Snow Cover Products. Remote Sens. 2017, 9, 774. https://doi.org/10.3390/rs9080774
Pan X, Li X, Cheng G, Chen R, Hsu K. Impact Analysis of Climate Change on Snow over a Complex Mountainous Region Using Weather Research and Forecast Model (WRF) Simulation and Moderate Resolution Imaging Spectroradiometer Data (MODIS)-Terra Fractional Snow Cover Products. Remote Sensing. 2017; 9(8):774. https://doi.org/10.3390/rs9080774
Chicago/Turabian StylePan, Xiaoduo, Xin Li, Guodong Cheng, Rensheng Chen, and Kuolin Hsu. 2017. "Impact Analysis of Climate Change on Snow over a Complex Mountainous Region Using Weather Research and Forecast Model (WRF) Simulation and Moderate Resolution Imaging Spectroradiometer Data (MODIS)-Terra Fractional Snow Cover Products" Remote Sensing 9, no. 8: 774. https://doi.org/10.3390/rs9080774
APA StylePan, X., Li, X., Cheng, G., Chen, R., & Hsu, K. (2017). Impact Analysis of Climate Change on Snow over a Complex Mountainous Region Using Weather Research and Forecast Model (WRF) Simulation and Moderate Resolution Imaging Spectroradiometer Data (MODIS)-Terra Fractional Snow Cover Products. Remote Sensing, 9(8), 774. https://doi.org/10.3390/rs9080774