On-Board GNSS/IMU Assisted Feature Extraction and Matching for Oblique UAV Images

Abstract

Feature extraction and matching is a crucial task in the fields of computer vision and photogrammetry. Even though wide researches have been reported, some issues are still existing for oblique images. This paper exploits the use of on-board GNSS/IMU (Global Navigation Satellite System/Inertial Measurement Unit) data to achieve efficient and reliable feature extraction and matching for oblique unmanned aerial vehicle (UAV) images. Firstly, rough POS (Positioning and Orientation System) is calculated for each image with cooperation of on-board GNSS/IMU data and camera installation angles, which enables image rectification and footprint calculation. Secondly, two robust strategies, including the geometric rectification and tile strategy, are considered to address the issues caused by perspective deformations and to relieve the side-effects of image down-sampling. According to the results of individual performance evaluation, four combinations of these two strategies are designed and comprehensively compared in BA (Bundle Adjustment) experiments by using a real oblique UAV dataset. The results reported in this paper demonstrate that the solution with the tiling strategy is superior to the other solutions in terms of efficiency, completeness and accuracy. For feature extraction and matching of oblique UAV images, it is proposed to combine the tiling strategy with existing workflows to achieve an efficient and reliable solution.

1. Introduction

In recent years, UAV has emerged as an attractive data acquisition platform for a wide range of photogrammetry and remote sensing tasks [1,2]. Compared with the conventional aerial- or satellite-based platforms, an UAV platform features rapid data acquisition, efficient cost and easiness of use. Generally, even with a non-metric camera integrated, an UAV-based photogrammetric system could efficiently capture images with extremely high spatial resolution because of relative lower flight heights. Thus, diverse applications across different fields of science have been documented [1].

At the same time, oblique imaging is another commonly adopted technique aiming at data acquisition from side-looking directions. It records both footprints and facades of targets, especially for buildings in urban environment when compared with the traditional vertical imaging systems. Nowadays, this technique is undergoing explosive development and becoming increasingly more important in the photogrammetric community, whose abilities for civil applications have been more and more reported [3,4]. It is rational that the combination of UAV platforms and oblique imaging systems could enhance both of their strengths. Some applications and experimental tests have been conducted and reported about the usage of oblique UAV images, including but not limited to urban forestry and urban greening [5] and 3D model reconstruction [6].

To use oblique UAV images for different scenarios with success, accurate camera poses are mandatorily required. In the conventional aerial photogrammetry, direct positioning and orientation of images can be achieved from combined and very precise GNSS/IMU (Global Navigation Satellite System/Inertial Measurement Unit) devices. However, a majority of market available UAVs are just equipped with low-cost GNSS/IMU sensors and the orientation data often cannot satisfy the accuracy requirements for direct orientation. Although some attempts have been made for direct geo-referencing of UAV images [7,8], almost all researches have focused on precise positioning while accurate orientation cannot be determined because of high costs of accurate miniature IMU sensors and maximum overload limitations of most UAVs on the market [7]. Therefore, combined bundle adjustment (BA), involving vertical and oblique images, becomes an established standard in almost all data processing pipelines, which is achieved by minimizing the total difference between predicted and observed image points. Prior to the combined BA, tie-point extraction and matching must be finished to set up the optimization problem.

In the communities of digital photogrammetry and computer vision, feature extraction and matching is a fundamental issue to ensure accurate information interpretation, such as dense point cloud generation, building 3D model reconstruction, etc. Therefore, lots of researches have been proposed to put forward the development of this technique towards the direction of precision and automation, which can be observed from the earliest corner detectors [9] to the newly invariant detectors [10]. Compared with classical corner detectors, in which matching operation is usually conducted by comparing pixel gray values of images in a fixed size window, invariant detectors use feature vectors to describe the local regions of interest points, which are called descriptors of the related points. Then, feature matching can be achieved through searching the nearest point with the smallest Euclidean distance between two descriptor sets. Among all invariant detectors, the SIFT (Scale Invariant Feature Transformation) outstands the others with best performance [10]. However, reliable matching cannot be achieved until the viewpoint variation does not exceed 50 degrees [11], which promotes the prosperous development of affine invariant descriptors [12]. In addition, to improve matching efficiency, other attempts have also been documented, including dimension reduction [13], binary descriptor [14] and hardware acceleration [15]. In a word, dozens of algorithms and free open-source software packages can be considered to perform tie-point extraction and matching for oblique UAV images.

Unfortunately, new challenges are imposed on tie-point extraction and matching for oblique UAV images. Major issues are listed as follows: (1) correspondence establishment between vertical and oblique images is extraordinary difficult because of different appearances mainly caused by occlusions and perspective deformations, which is much more severe in urban environment with dense buildings; (2) the loss of location accuracy and the reduction of tie-point number would be caused by the commonly adopted down-sampling strategy in order to adapt to the limited memory capacity when extracting features from high resolution images; and (3) because of the relative small footprints of UAV images and the adoption of oblique cameras, many more images are collected for a specified surveying area when compared with traditional aerial images, which complexes the combinatorial complexity for match pair selection. Therefore, extra considerations should be gained for sufficient and precise tie-point extraction and matching with impressive efficiency. In this study, we mainly focus on the first and the second issues.

In the literatures, for relieving perspective deformations, affine-invariant regions have been deeply exploited to compute affine-invariant descriptors [12]; however, these methods can cause either decreases in the amount of extracted features or performance losses in the cases of slightly affine deformations [11]. Differing from internet photos, images captured by photogrammetric systems usually include rough or precise positioning and orientation data, which is obtained by either non-professional or professional GNSS/IMU devices. Therefore, perspective deformations can be globally relieved for each image rather than for per interest point. Thus, Hu et al. [16] injected this strategy into the tie-point matching pipeline of oblique aerial images. It was used as a pre-processing step prior to tie-point extraction. With the use of FAST corner detector [17] and BRIEF descriptor [18], sufficient and well-distributed tie-points were extracted. Similarly, on-board GNSS/IMU data can also be used for geometric rectification of oblique UAV images, which possesses the potential to be considered as a possible solution to address the first issue.

To decrease the negative effects of image down-sampling on the loss of location accuracy and the reduction of tie-point number, the divide-and-conquer or the tiling strategy maybe the most obvious and reliable solution. In general, moderate changes in scale, rotation and affinity can be tolerated by most elaborately designed detectors and descriptors, such as the SIFT-based algorithms, which aim for low-resolution and low-accuracy tasks [19]. To cope with high-precision surveying and mapping tasks in the photogrammetric field with high-resolution images, some solutions have been proposed. Novák et al. [19] combined a recursively tiling technique with the existing tie-point extraction and matching algorithms and attempted to process images with high spatial resolution. The tiling strategy can be regarded as a semi-global solution, which is more global than affine-invariant detectors and more local than methods based on global geometric rectification. To decrease the side-effects on high computational costs, Sun et al. [20] proposed a similar algorithm to extract and match tie-points for large images in large scale aerial photogrammetry, where a 2D rigid transformation was adopted to create image relationships and a single recursion level is used to tile images. In their researches, the divided-and-conquer strategy can not only increase the number of extracted points, but also decrease the risk of loss of location accuracy because it can work on images with original spatial resolution. Therefore, in this paper, we attempt to exploit the validity of using the tiling strategy for feature extraction and matching of oblique UAV images, and also to verify the validity of using on-board GNSS/IMU data to predict corresponding tiles. This could be an alternative solution to address the second issue mentioned above.

In this paper, we exploit the use of on-board GNSS/IMU data to assist feature extraction and matching of oblique UAV images. Because original GNSS/IMU data is recorded in the navigation system, orientation angle transformation is firstly applied to convert original navigation data to the coordinate system used in this study. Secondly, two possible strategies, including the global geometric rectification and tiling strategy, are comprehensively evaluated in bundle adjustment tests from aspects of efficiency, completeness and accuracy. Finally, an optimal solution is recommended to design the GNSS/IMU assisted workflow for feature extraction and matching.

The remainder of this paper is organized as follows. Section 2 describes the study site and one test dataset. The methodology applied in this study, including orientation angle transformation, feature extraction and feature matching, is then introduced. In Section 3, performance of these two strategies on feature extraction and matching is evaluated and compared by using BA experiments. In addition, some aspects of these two strategies are discussed with related researches in Section 4. Finally, Section 5 presents the conclusion and further studies.

2. Materials and Methods

To relieve problems caused by perspective deformations and image down-sampling in feature extraction and matching for oblique UAV images, this study turns to exploit the use of on-board GNSS/IMU data to address these issues. An overview of the workflow is presented in Figure 1. For the adaption of the final solution to consumer-grad UAVs, the GNSS/IMU data is collected from on-board integrated flight controllers, which features relative lower positioning and orientation accuracy compared with professional sensors. The GNSS/IMU data is firstly transformed from the navigation system to a local tangent plane (LTP) coordinate system used in this study, which is used for rough POS calculation. Then, the POS data is used as auxiliary data in three methods, including rough POS aided global geometric rectification, tile-based feature extraction and feature matching. Finally, a series of solutions are designed by combining the three methods. Meanwhile, comprehensive comparison tests are conducted to select the optimal solution for efficient feature extraction and matching of oblique UAV images with sufficient point number. The details of the study are presented in the following subsections.

2.1. Study Site and Test Data

The study site locates in Pingtan County of Fuzhou, China. It is an island to the east of the mainland, which is covered by low buildings and parterres as shown in Figure 2. The building roofs are characterized by repetitive patterns and homogenous textures, which impose many difficulties on automatic image matching. In addition, the surroundings of the study site are bare land, which are either underexploited clearings or suburban highways, and a river comes along both the north and the east sides of the test site.

For outdoor data acquisition campaign, a multi-rotor UAV, ZEROTECH E-EPIC (manufactured by ZEROTECH Corporation at Beijing, China), is employed in this study. The nominal hovering accuracy (in GPS mode) is 1.5 m and 0.5 m in the horizontal and vertical directions, respectively. Considering the movement of UAV platforms, the positioning accuracy would be lower than the nominal specifications. Because of the usage of non-professional IMU devices and the misalignment of cameras installation, the deduced orientation accuracy should be near one degree (the orientation accuracy of the IMU device would be near 0.2 degrees). The UAV is composed of a non-professional positioning and orientation sensors to provide rough navigation information, an autopilot circuit board and a flight controller with display and control systems. All the models are provided by the manufacturer and none of them are modified in this study. Besides, the UAV system enables three operation modes, which consists of manual, semi-automatic and automatic modes. The semi-automatic mode is used in this study, where takeoff and landing of one flight are assisted by operators. The details of specifications for the imaging system and flight campaign are listed in

Table 1. Specifications of photogrammetric system and flight campaign.

Item Name	Value
UAV type	multi-rotor
Flight height (m)	300
Camera model	Sony ILCE-7R
Focal length (mm)	35
Sensor size (mm × mm)	35.9 × 24.0
Camera mount angle (${}^{\circ }$)	nadir: 0 oblique: 45
Image size (pixel × pixel)	7360 × 4912
Forward/side overlap (%)	64/48
GSD (cm)	4.20/5.60

. For image capture, a photogrammetric device carrying one Sony ILCE-7R camera (manufactured by Sony electronics (Wuxi) Co. LTD at Wuxi, China) is designed and integrated with the UAV platform. The camera has a more than 36 Mpixel (7360 by 4912 pixels) sensor with physical dimensions of 35.9 mm by 24.0 mm and focal length of 35 mm. In this study, the original images with distortions are used for tests of feature extraction and matching. To enable precise photogrammetric measurement, the used camera has been calibrated in the laboratory. The Brown calibration mode [21] is selected, which is formulated by eight parameters, including one for focal length, two for principle point, three for coefficients of radial distortions and two for coefficients of tangent distortions. Considering that only rough GNSS/IMU data is required, system calibration for sensor integration does not conducted in this study because the value of lever-arm offsets is much smaller than the footprint dimensions of images and because the value of bore-sight angles is much smaller than the angles of camera installation.

To simulate data acquisition abilities of penta-view camera systems, two individual campaigns are conducted over the study site in which one campaign with zero roll and pitch camera mounting angles is configured for vertical image capture and the other campaign with zero roll and 45${}^{\circ }$ pitch angles is configured for oblique image capture in the directions of north, south, east and west, which are illustrated by Figure 3a,b, respectively. We can see that each location in the test site can be observed from five directions, including vertical and oblique views. The dataset, simulating penta-view imaging systems, is illustrated in Figure 4, where V stands for the nadir images and N, S, W and E indicate the images captured in the north, south, west and east directions, respectively. At last, a total of 157 vertical and oblique UAV images over the study site are collected under the flight height of 300 m relative to ground. The GSD (Ground Sampling Distance) values for vertical and oblique images are 4.20 cm and 5.60 cm, respectively. Therefore, overlap degrees in forward and side directions are 64% and 48%, respectively.

2.2. Methodologies

On-board GNSS/IMU assisted feature extraction and matching strategy follows a procedure which encloses four steps: (1) orientation angle transformation; (2) feature extraction for images; (3) feature matching for image pairs and (4) geometric verification for outlier removal. In this study, some modifications are injected into the second and the third steps to evaluate and address special issues on feature extraction and matching for oblique UAV images.

2.2.1. Orientation Angle Transformation

Definitions of orientation angles derived by the combined GNSS/IMU sensors differ from those used for direct geo-referencing, in which the former is described with respect to the navigation system (n-system) and the latter is measured in the object coordinate system (e-system) [22]. Therefore, orientation angles must be transformed prior to its further usages. With aids of the Earth Centered Earth Fixed (e-system) coordinate system, orientation angles can be converted from the n-system to the e-system by a sequence of rotation matrixes [23], as represented by Equation (1)

$$R_E^i={\left(R_i^c\right)}^T\times {\left(R_c^b\right)}^T\times {(R_e^{n_0}\times {\left(R_e^{n_i}\right)}^T\times R_b^{n_i})}^T\times {\left(R_n^E\right)}^T$$

(1)

where $R_b^{n_i}$ is the rotation matrix used to transform a vector from the body system (b-system) to the n-system using the sequence of rotations defined by heading, pitch and roll $(\mathsf{\Psi },\mathsf{\Theta },\mathsf{\Phi })$; $R_E^i$ is the rotation matrix defining the transformation from e-system to the image space system (i-system), from which orientation angles, omega, phi and kappa $(\omega ,\varphi ,\kappa )$, can be calculated; $R_e^{n_0}$ and $R_e^{n_i}$ are used to define the transformations from the e-system to the n-system with origins $(\varphi ,\lambda )$ labeled by $n_0$ and $n_i$, respectively; $R_n^E$ is a fixed matrix to correct the orientations of coordinate axes from the n-system to the e-system; finally, $R_i^c$ and $R_c^b$ define the transformation from the i-system to the sensor system (c-system) and the transformation from the c-system to the b-system, respectively. Details of each matrix are presented in the section Appendix A.

The matrixes $R_i^c$ and $R_c^b$ have different definitions with varying camera installations and image space systems. In this study, the image space system coincides with the system used in the field of computer vision, which is a right-hand Euclidean coordinate system with X and Y axes pointing to the right side and the bottom side of the camera, respectively. For a classical penta-view oblique imaging system with camera installation as illustrated in Figure 5, orientation angles of these two matrixes are listed in

Table 2. Orientation angles for the transformation between b-system and i-system.

Item Name	Value
Camera Orientation	Front	Back	Left	Right	Vertical
Roll (${}^{\circ }$)	0.0	0.0	45.0	−45.0	0.0
Pitch (${}^{\circ }$)	45.0	−45.0	0.0	0.0	0.0
Heading (${}^{\circ }$)	0.0	0.0	0.0	0.0	0.0
Image rotation (${}^{\circ }$)	90.0	−90.0	0.0	180.0	90.0

, where the roll, pitch and heading angles define three consecutive rotations around X, Y and Z axes, respectively. These three angles are used to calculate the transformation matrix $R_c^b=R_x\left(r\right)\times R_y\left(p\right)\times R_z\left(h\right)$. Similarly, the image rotation angle defines the transformation matrix $R_i^c=R_z\left(rot\right)$. Thus, for the test data used in this study, the campaign for vertical images has the same angle installations as the vertical camera and the other campaign for oblique images has identical configurations as the front camera as illustrated in Figure 5. By using on-board GNSS/IMU data and camera installation angles, original orientation angles are converted to the e-system, which is defined as a LTP system with origin located in test center, and rough positioning and orientation (POS) can be calculated for each image.

2.2.2. Feature Extraction

Instead of methods based on local affine-invariant regions, the rough POS is adopted to perform global geometric rectification on each image for relieving perspective deformations, which are mainly caused by different imaging angles. This can be considered as a pre-processing step prior to feature extraction, which is similar to the strategy used in [16]. However, in this study, feature extraction is performed by using the SIFT [11] algorithm, rather than the FAST detector [17] and the BRIEF descriptor [18]. On the one hand, rough POS data cannot completely remove perspective deformations as well as image rotations, which would cause performance degradation because the BRIEF descriptor is neither scale invariant nor rotation invariant [14]. On the other hand, hardware acceleration of the SIFT algorithm, such as the GPU-based implementation [15], can also provide competitive efficiency when compared with the FAST detector and the BRIEF descriptor. For one image pair, computational costs are no longer an issue worthy of too much concern. Thus, we can evaluate the effectiveness of global geometric rectification on feature extraction and matching as much as possible because negligible influence comes from the descriptor itself.

2.2.3. Feature Matching

Combinational complexity for pairwise matching is quadratic in the number of images. Because of the relative small footprints of UAV images and the adoption of oblique cameras, the number of images collected for a specified surveying area would noticeably increase when compared with traditional aerial photogrammetry. Thus, high time consumption would be caused by exhausted pairwise matching methods. Although strategies have been proposed in some studies [24,25,26,27], almost all methodologies are either merely dependent on a direct adjacent principle or only adaptive to vertically captured images, which leads to the existence of vast redundant match pairs and the limitation of usages for oblique images. In this study, the strategy documented in [6] is adopted for match pair selection. This method extracts essential image pairs using a maximal spanning tree expansion algorithm with the aids of rough POS data and camera installation angles, which satisfies the requirements of oblique UAV images.

The divide-and-conquer method is a reliable solution to process large size and high resolution images. For feature extraction, large images are usually tiled into blocks with small dimensions and features are extracted individually from each block. Similarly, this strategy can also be adopted for tile-based feature matching in which the primary task is to estimate the transformation parameters for corresponding block searching, as descripted in the work of [20]. A 2D rigid transformation can be utilized for aerial images with zero roll and pitch angles imposed on aerial platforms, but not for oblique UAV images. To cope with this issue, two possible solutions can be used. Without POS data, a homography matrix estimated from seed points can establish the geometric relative relationship between two images, as shown in Figure 6a. By using POS data, the relationship can be deduced from imaging geometry where a block from the first image plane is firstly projected onto a ground plane, and then reprojected onto the second image plane, as illustrated in Figure 6b.

After finding corresponding blocks, feature matching is implemented by comparing two sets of feature descriptors using a nearest neighbor method searching [28]. To remove outliers existed in initial correspondences, some tests are also performed. Firstly, a ratio test, similar to the work in [11], is performed for candidates in which a correspondence can be identified when the ratio between the shortest and the second shortest distances is lower than a specified threshold (0.8 in this study). Secondly, a cross check is executed on the retained correspondences, which retrieves just the matches found in both directions. These two tests are conducted for feature matching on each block. Finally, a geometric verification is applied on the whole image by estimating a fundamental matrix within the RANSAC (RANdom SAmple Consensus) algorithm [29].

3. Experimental Results

In the experiments, we would evaluate the performance of two potential solutions, including the global geometric rectification and tiling strategy, for feature extraction and matching of oblique UAV images. Firstly, the rough POS of each image is calculated from on-board GNSS/IMU data and camera installation angles, which enables image pair selection and geometric rectification. Secondly, the performance evaluation on feature matching is individually conducted and analyzed in terms of the number and distribution of correspondences. Finally, various combinations of above mentioned methods would be compared from the aspects of efficiency, completeness and accuracy, and the best solution for feature extraction and matching of oblique UAV images is proposed. In this study, all experiments are executed on an Intel Core i7-4770 PC (manufactured by Micro-Star Corporation at Shenzhen, China) on the Windows platform with a 3.4 GHz CPU and a 2.0 G GeForce GTX 770M graphics card.

3.1. Orientation Angle Transformation

Two individual campaigns are configured for outdoor data acquisition in this study. The first campaign is conducted for capturing nadir images with near zero roll and pitch angles imposed on camera installation. To collect oblique images, the camera is mounted with near 45${}^{\circ }$ pitch angle in the second campaign. Therefore, by using on-board GNSS/IMU data and camera installation angles, exterior orientation (EO) parameters, consisted of positioning and orientation angles, are computed for each image with respect to an object coordinate system, which is set as a LTP coordinate system with origin in the site center.

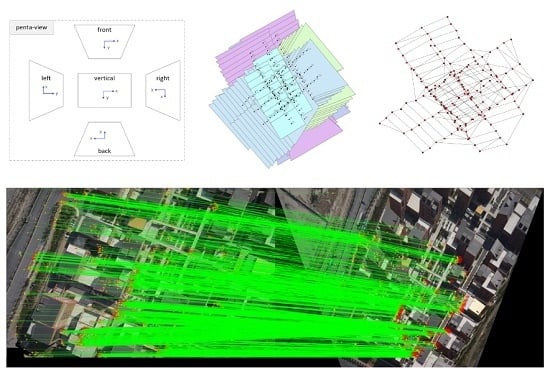
The rough EO parameters enable computation of image footprints as shown in Figure 7. It is clearly shown that two tracks are set for the vertical direction and three tracks for east, west, south and north directions, respectively. In addition, high overlap degree between footprints can be observed, especially for oblique images. If just considering a direct overlap principle for image pair selection, too many redundant image pairs would be preserved and fed into the process of feature matching. Thus, high time consumption would be frequently required even for data processing of UAV images collected from small areas.

Figure 8a presents the result of image pair selection just using an overlap principle where one image pair would be preserved only if the dimension of overlap exceeds half of the footprint size. We can see that a total of 4430 image pairs are found based on the principle and redundant image pairs can be clearly observed, especially near the center of the study site. Alternatively, in this study, the maximal spanning tree expansion strategy is used to remove these redundant image pairs. The strategy depends on a two-stage algorithm, named as MST-Expansion, for the further simplification of initial image pairs and extracted image pairs are shown in Figure 8b. Compared with the direct overlap principle, the MST-Expansion takes into count the topological connection relationship of image footprints and can dramatically reduce the number of image pairs while preserving most of essential image pairs. Finally, there are 309 image pairs retained for the test dataset. In the following sections of this study, image pairs generated from the MST-Expansion algorithm would participate in the further processing and analysis.

3.2. Performance Evaluation of Geometric Rectification

In this study, global geometric rectification is the process to simulate vertical imaging when the EO parameters of images are known. By using the calculated POS data, rectification operations can be executed on original oblique images to relieve perspective deformations. In order to evaluate the performance of rectification on feature matching, two image pairs, covering a build-up area and a bare-land area, are selected and matching results are shown in Figure 9 and Figure 10, where oblique images are rectified. Because of serious occlusions of buildings and homogeneous textures of roofs, most correspondences are extracted on the ground, such as roads and parterres as shown in Figure 9a, for the test without image rectification. With image rectification, the same situation occurs as illustrated in Figure 9b. The distribution of correspondences is not obviously improved with the match number increased from 35 to 58, because almost all newly matched points are centralized in the regions illustrated by red ellipses. On the contrary, geometric rectification can improve both the number and distribution of correspondences for the test in bare-land area as shown in Figure 10b. The number of matches increases from 108 to 209 and the distribution of correspondences is more uniform compared with the results presented in Figure 10a. Therefore, with the aids of rough POS data of oblique images, global geometric rectification can to some extent relieve perspective deformations and increase the number of matches for both build-up and bare-land areas. However, it cannot improve the distribution of correspondences for images with dense buildings.

Obviously, geometric rectification is achieved through image resampling. The parts near photo nadir points of oblique images would be seriously compressed, which is equivalent to resolution down-sampling and image dimension reduction. Therefore, geometric rectification also has impact on feature extraction in terms of number and distribution. Figure 11 shows the results of feature extraction influenced by geometric rectification, where Figure 11a,b are results of feature extraction performed on the original and rectified images, respectively. It is noted that the bottom part of the oblique image is near the photo nadir point and would be compressed with respect to the top part. The experimental result shows that there are 11,424 features extracted from the rectified image while 9681 features are extracted from the original image. By the further analysis of four sub-images, some findings can be observed: (1) more features are extracted from the top part of the rectified image than that of the original images by comparing sub-images 1 with 3; (2) the density of features near the bottom part of the rectified image is sparser than that in the original image by comparing sub-images 2 with 4. Therefore, global geometric rectification increases the total number of features, but causes the un-uniform distribution of features on the image plane.

3.3. Performance Evaluation of Tiling Strategy

Corresponding block searching is the primary task to achieve the tiling strategy, which can be implemented based on two solutions. Without the assistant of POS data, seed points are firstly extracted from a down-sampled image, and homography estimation is then executed to calculate transformation parameters. This solution, named as ‘HE’ method, requires computational costs for generating seed points, but does not rely on the accuracy of the auxiliary data sources. The other solution is to predict corresponding blocks by using images’ POS data, which is referred as the ‘POS’ method. Besides, depending on whether or not the tiling strategy is used for feature extraction, two extra situations are existed, where ‘NE’ and ‘TE’ stands for feature extraction without tiling strategy and feature extraction with tiling strategy, respectively. Therefore, in this subsection, a total of four conditions would be compared and analyzed.

To compare the performance of these four combinations, four tests on feature extraction and matching are conducted and the results are listed in Figure 12. Because no matches are retrieved by using the POS-NE method, correspondences of the HE-NE, HE-TE and POS-TE methods are presented in Figure 12a–c, respectively. In addition, the number of correspondences is 53, 2728 and 15, respectively. From visual inspection and statistical analysis of the matching results, we can see that: (1) although the number of correspondences of the HE-NE method is almost equal to that of the method without tile strategy as shown in Figure 9b, well-distribution of correspondences can be observed from Figure 12a; (2) with tiling strategy used in feature extraction, the number of matches is dramatically increased and the distribution of matches is noticeably improved by checking Figure 12b; and (3) the least number of matches is retrieved by the POS-TE method, as shown in Figure 12c, which could be mainly caused by the inaccurate POS data. Because of the inaccurate POS data for corresponding block prediction and the less number of features extracted by the non-tiling strategy, no correspondences are matched from the POS-NE method. Thus, to improve both number and distribution of correspondences, tile-based feature extraction is recommended to be utilized in collaboration with tile-based matching. Besides, homography estimation is a preferred solution for corresponding block retrieving when no accurate POS data can be accessed.

3.4. Comparison of Various Combined Solutions

3.4.1. Solution

In this subsection, the main purpose is to find an optimal solution for feature extraction and matching of oblique UAV images. Consequently, various combined solutions, consisted of above mentioned strategies, are designed and comprehensive comparisons would be conducted in terms of efficiency, completeness and accuracy. The details of combined solutions are listed in

Table 3. Details of combined solutions for feature extraction and matching.

Solution	Description
NR-NT	no rectification & no tiling
R-NT	rectification & no tiling
NR-T	no rectification & tiling
R-T	rectification & tiling

, where a total of four solutions have been promoted. The solution with the use of the tiling strategy indicates that the strategy is adopted in both feature extraction and matching because the tiling strategy could noticeably increase the correspondence number, which has been verified in the Section 3.3. In addition, the homography estimation method is adopted for corresponding block searching because rough POS data cannot enable accurate prediction. Designs of these four solutions follow the criterions: (1) the first solution is designed for the situation that none of these two strategies is adopted; (2) the second and third solutions aim to assess the performance of the geometric rectification and tiling strategy; and (3) to evaluate the combined performance, the forth solution is designed and evaluated in this study.

3.4.2. Efficiency

In this study, the SiftGPU software package [15], a hardware acceleration version of the SIFT algorithm based on GPU (graphic processing unit), is adopted for feature extraction and matching. The default parameters are used with the maximum image dimension of 3200 pixels, the ratio test threshold of 0.8 and the distance threshold of 0.7. Thus, images are down-sampled to the dimension no more than 3200 pixels when the tiling strategy is not prepared, and matches would be removed when either ratio rests or Euclidean distances surpass the corresponding threshold. In the geometric verification based on the fundamental matrix estimation, the maximum epipolar error is set as one pixel to guarantee high inlier ratio among all matches. In addition, for the tiling strategy, the block size is configured as 1024 pixels for both feature extraction and matching, which is a compromise between computational efficiency and feature number as discussed in the work of [20].

Feature extraction and matching are executed on 157 images and 309 image pairs, respectively. Time consumption is illustrated in Figure 13. It is clearly shown that the least computational costs are need in feature extraction of the NR-NT solution and almost the same and the highest time consumption is observed from feature extraction of the R-NT and R-T solutions. Approximately, for feature extraction, the ratio of time consumption is 7.67 between solutions with and without geometric rectification, which means that 6.67 times of more computational costs are required for image rectification with respect to the costs of feature extraction. Similarly, the ratio between solutions with and without the tiling strategy is about 1.40, which indicates that very little time costs are need in the tile-based solutions compared with the solutions using geometric rectification.

In addition, for feature matching, time costs of the NR-NT and the R-NT solutions are almost identical because geometric rectification cannot dramatically increase the number of extracted features. For solutions with the tiling strategy, including the NR-T and R-T solutions, many more features are detected, which leads to more time costs on feature matching. The ratio of time costs between solutions with and without the tiling strategy is about 3.13. Finally, the statistical results of time consumption are shown in

Table 4. Time consumption of feature extraction and matching (in minutes).

Solution	Extraction	Matching	Total
NR-NT	3.226	1.314	4.540
R-NT	24.746	1.419	26.165
NR-T	4.507	4.646	9.153
R-T	25.798	3.898	29.696

. We can see that the highest total time costs are consumed by the solutions with geometric rectification while the least costs from solutions without geometric rectification.

3.4.3. Completeness

For completeness analysis, bundle adjustment experiments are conducted and sparse 3D models are used for comparison, including the number of connected images and 3D points. In this study, an incremental structure from motion (SfM) software package is used for BA tests, which is developed at home and described in detail in the work of [30]. The only inputs of the BA software are correspondences generated from feature matching due to the fact that it utilizes an incremental procedure for camera pose estimation and 3D point triangulation.

The statistical results of reconstructed images and points are listed in

Table 5. Number of reconstructed images and points.

Solution	No. Images	No. Points
NR-NT	157/157	61,565
R-NT	157/157	68,012
NR-T	157/157	333,034
R-T	157/157	290,462

. We can see that: (1) all images are successfully connected by using these four solutions; (2) the largest number of points is reconstructed in the NR-T solution, while the least number of points from the NR-NT solution; and (3) although geometric rectification is applied in the R-T solution, the number of recovered points is less than that of the NR-T solution, which can explained by the non-uniform distribution of feature points caused by image rectification as shown in Section 3.2. In conclusion, the tiling strategy can dramatically increase the number of reconstructed points than geometric rectification. The sparse 3D models of these four solutions are presented in Figure 14.

3.4.4. Accuracy

Accuracy assessment is also conducted by using the BA experiments. In this subsection, the free and open-source photogrammetric software package MicMac [31] is also adopted except for the SfM software package. MicMac provides a complete set of tools to compute and reconstruct 3D models from overlapped images. Among all functions of MicMac, the Tapioca function is used for feature extraction and matching with multi-core parallel computation technology and the Apero function provides abilities for image orientation with or without camera self-calibration. Because of different definitions of camera calibration parameters, a small subset of images with high overlap degree are firstly chosen. Then, feature extraction and matching are executed for the image set. Finally, image orientation with self-calibration is performed to estimate an initial set of camera parameters, which would be used in the latter image orientation for the whole image set.

Because correspondences have been extracted from the proposed solutions, just the orientation tool Apero is used for the assessment of orientation accuracy for the whole image set. To guarantee high precision, the self-calibration is also configured in the orientation of the whole dataset. The RMSEs (root mean square errors) of BA tests in both MicMac and SfM are listed in

Table 6. RMSE of bundle adjustment in MicMac and SfM (in pixels).

Solution	MicMac	SfM
NR-NT	0.744	0.402
R-NT	0.748	0.400
NR-T	0.586	0.291
R-T	0.580	0.299

, where SfM stands for the BA software developed at home. By the analysis of the orientation results, some conclusions can be made: (1) geometric rectification cannot improve the orientation accuracy by comparing the RMSEs of the NR-NT and R-NT solutions; (2) the tiling strategy can noticeably improve orientation accuracy by comparing the RMSEs of the NR-NT and NR-T solutions; (3) even with the combination of these two strategies in the R-T solution, ignorable improvements of orientation accuracy can be observed from the RMSE in MicMac. In addition, side effects are also observed from the BA test in SfM because the estimated accuracy from the SfM is smaller than that of the MicMac. The main reason is that outlier removal is also performed in the processing of image orientation. However, for MicMac, all input matches are considered as true observations and used in bundle adjustment. To ensure reliable feature extraction and matching for oblique UAV images, the solution NR-T is proposed from the comparison results of BA tests.

4. Discussion

This research evaluates the performance of the global geometric rectification and tiling strategy for feature extraction and matching of oblique UAV images. To achieve these two strategies, rough POS for each image is calculated by using on-board GNSS/IMU data and camera installation angles. In addition, four combined solutions are widely compared and analyzed from aspects of efficiency, completeness and accuracy in BA tests. The experimental results show that the solution integrated with the tiling strategy is superior to the other solutions.

Although global geometric rectification could to some extent relieve perspective deformations between oblique images, it does not noticeably increase the number of correspondences, as well as improving the distribution. In the experiments reported in this paper, the performance of geometric rectification has been evaluated by using one image pair of build-up area and one image pair of bare-land area, as presented in Figure 8 and Figure 9, respectively. The results demonstrate that this strategy can increase the number of correspondences in both build-up and bare-land areas. However, the distribution of correspondences is not noticeably improved, especially in the build-up area. In the study of [16], the same operation was executed on aerial oblique images of a build-up area and satisfying results were gained even with the BRIEF descriptor, which is neither scale invariant nor rotation invariant [14]. Main reasons can be deduced from some aspects. Firstly, aerial oblique images are usually captured with relative higher flight heights. Under the condition that the same oblique angles are used for camera installation, occlusions become more serious in UAV images, especially in build-up areas, which leads to fewer correspondences extracted from ground points. Secondly, metric cameras with long focal length are standard instruments in aerial photogrammetry tasks. On the contrary, non-metric and low-cost digital cameras are equipped with UAV platforms, which have relative shorter focal length. Thus, perspective deformations are of severity in UAV images. Finally, because of weak stability of UAV platforms, oblique angles of images would exceed pre-designed values, which are mainly caused by winds. Thus, remainder of deformations still exists in images rectified by using the rough POS data. In conclusion, geometric rectification is not suitable for the pre-processing of oblique UAV images aiming at feature extraction and matching when compared with its usage in aerial oblique images.

On the contrary, promising results have been obtained from the use of the tiling strategy in both feature extraction and matching. In the comparison tests, the NR-T solution with the tiling strategy outperforms the other solutions in terms of efficiency, completeness and accuracy. The total time spent on feature extraction and matching is about one third of that used in the solutions with geometric rectification. In addition, this solution can achieve BA tests with the lowest RMSEs and the maximum number of reconstructed points. Compared with geometric rectification, this strategy can not only increase the number of matches, but also improve their distribution. The number of correspondences can be noticeably increased due to the fact that when feature matching is restricted to the corresponding tiles, the ratio of the smallest Euclidian distance between two descriptor sets to the second smallest one would be smaller than the specified threshold with higher probability [20]. Besides, when original images are tiled, feature extraction can be applied on images with full resolution. Similarly, it also improves the distribution of correspondences because they would be found within each tile region. The tiling strategy is regarded as a semi-global solution, which is more local than methods with global geometric verification [19].

To use the tiling strategy in feature extraction and matching, corresponding block searching has been achieved through homography estimation between image pairs in this study because on-board GNSSS/IMU is not precious enough for corresponding block prediction. Nowadays, most of market-available UAVs are equipped with non-professional GNSS/IMU devices with low positioning and orientation accuracy. In order to improve the accuracy, some other attempts could be made, such as the elimination of GNSS multipath and visual localization. In the urban environment, one of the main factors causing the degradation of positioning precision is the GNSS multipath because of the relative lower flight height of UAV platforms. Then, some attempts would be made for the GNSS multipath mitigation [32]. In addition, visual localization is an important clue for the direct positioning of UAVs, which can adapt to some special situations without GNSS signals. With the aids of existing aerial images or urban structure data [33], visual localization technique could furtherly decrease the positioning errors, which is about several meters for most market-available UAVs. In the future, with the positioning and orientation accuracy improvement of UAV platforms, the prediction task can be implemented without homography estimation.

In addition, the combination of these two strategies is also analyzed and verified in this study, which corresponds to the R-T solution. The experimental results show that competitive accuracy of BA tests can be achieved from the solution, but more computational costs are observed for image rectification. Meanwhile, image rectification leads to the non-uniform distribution of feature points, as well as does not increase the number of reconstructed points. Therefore, in this study, the NR-T solution is proposed for feature extraction and matching of oblique UAV images.

5. Conclusions

This study exploits the use of on-board GNSS/IMU data to achieve efficient and reliable feature extraction and matching for oblique UAV images. Firstly, on-board GNSS/IMU data is transformed from the navigation system to the object coordinate system used in this study, and it is used for the calculation of rough POS for each image by cooperating with camera installation angles. Secondly, two strategies, including the global geometric rectification and tiling strategy, are tested and evaluated to cope with the challenges of oblique image matching and the side-effects of image down-sampling. Finally, comprehensive comparison and analysis are conducted in terms of efficiency, completeness and accuracy in BA tests. As shown in the experiments, the solution integrated with the tiling strategy outperforms the other solutions from aspects of the number and the distribution of correspondences.

In this study, the spatial relationships between image pairs are determined by estimating the homography transformation because of the low precision of on-board GNSS/IMU devices. In the further, some other tests would be evaluated for UAV platforms equipped with high precious sensors. In addition, BA results in the MicMac show that outliers still exist in correspondences even though strict thresholds are adopted for mismatch filtering. Thus, high level constrains would be considered for outlier removal in future studies.