Wave Height Estimation from Shadowing Based on the Acquired X-Band Marine Radar Images in Coastal Area
Abstract
:1. Introduction
2. The Estimation of Wave Height Based on the Shadow Statistics
2.1. The Estimation of the Shadow Gray-Scale Threshold
2.1.1. The Shadow Edge Detection of the Radar Image
2.1.2. The Elimination of the Isolated Noise Points
2.1.3. The Calculation of the Shadow Gray-Scale Threshold
2.2. The Calculation of the Illumination Ratio of the Radar Image
2.3. The Estimation of the Average RMS Wave Surface Slope
2.4. The Estimation of the Significant Wave Height
3. The Improved Method for Retrieving the Significant Wave Height
3.1. The Definition of the Sea Surface Slope
3.2. Retrieving the Significant Wave Height Based on the Sea Surface Slope in Near-Shore Area
3.3. The Improved Method for Retrieving Wave Height Based on the Sea Surface Slope
4. The Results and Analysis of the Experiment
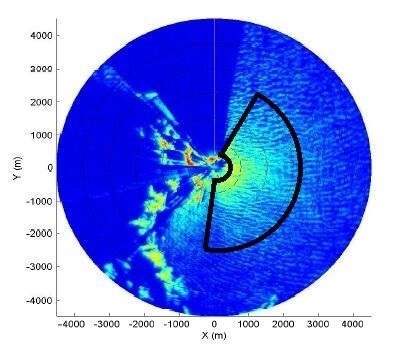
4.1. Field Data
4.2. The Sparse Processing of Radar Image
4.3. Experimental Results and Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, Z.; Pan, J.; He, Y.; Devlin, A. Estimate of tidal constituents in nearshore waters using X-band marine radar image sequences. IEEE Trans Geosci. Remote Sens. 2016, 54, 6700–6711. [Google Scholar] [CrossRef]
- Chen, Z.; He, Y.; Zhang, B.; Qiu, Z. Determination of nearshore sea surface wind vector from marine X-band radar images. Ocean Eng. 2015, 96, 79–85. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, J.-K.; Lu, Z. A novel successive cancellation method to retrieve sea wave components from spatio-temporal remote sensing image sequences. Remote Sens. 2016, 8, 607. [Google Scholar] [CrossRef]
- Wei, Y.; Lu, Z.; Huang, Y. Wave parameters inversion from X-band marine radar image sequence based on the novel dispersion relation band-pass filter on the moving platform. J. Comput. Theor. Nanosci. 2016, 13, 5470–5477. [Google Scholar] [CrossRef]
- Dankert, H.; Horstmann, J.; Rosenthal, W. Wind- and wave-field measurements using marine X-band radar-image sequences. J. Ocean. Eng. 2005, 30, 534–542. [Google Scholar] [CrossRef]
- Huang, W.; Gill, E.; An, J. Iterative least-squares-based wave measurement using X-band nautical radar. IET Radar Sonar Navig. 2014, 8, 853–863. [Google Scholar] [CrossRef]
- Serafino, F.; Lugni, C.; Soldovie, F. A novel strategy for the surface current determination from marine X-band radar data. IEEE Geosci. Remote Sens. Lett. 2010, 7, 231–235. [Google Scholar] [CrossRef]
- Shao, W.; Li, X.; Sun, J. Ocean wave parameters retrieval from TerraSAR-X images validated against buoy measurements and model results. Remote Sens. 2015, 7, 12815–12828. [Google Scholar] [CrossRef]
- Dankert, H.; Rosenthal, W. Ocean surface determination from X-band radar-image sequences. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Shen, C.; Huang, W.; Gill, E.W.; Carrasco, R.; Horstmann, J. An algorithm for surface current retrieval from X-band marine radar images. Remote Sens. 2015, 7, 7753–7767. [Google Scholar] [CrossRef] [Green Version]
- An, J.; Huang, W.; Gill, E.W. A self-adaptive wavelet-based algorithm for wave measurement using nautical radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 567–577. [Google Scholar]
- Senet, C.; Seemann, J.; Ziemer, F. The near-surface current velocity determined from image sequences of the sea surface. IEEE Trans. Geosci. Remote Sens. 2001, 39, 492–505. [Google Scholar] [CrossRef]
- Chuang, L.Z.-H.; Wu, L.-C. Study of wave group velocity estimation from inhomogeneous sea-surface image sequences by spatiotemporal continuous wavelet transform. IEEE J. Ocean. Eng. 2014, 39, 444–457. [Google Scholar] [CrossRef]
- Gangeskar, R. An algorithm for estimation of wave height from shadowing in X-band radar sea surface images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3373–3381. [Google Scholar] [CrossRef]
- Nieto-Borge, J.C.; Guedes Soares, C. Analysis of directional wave fields using X-band navigation radar. Coast. Eng. 2000, 40, 375–391. [Google Scholar] [CrossRef]
- Ludeno, G.; Reale, F.; Dentale, F.; Carratelli, E.P.; Natale, A.; Soldovieri, F.; Serafino, F. An X-band radar system for bathymetry and wave field analysis in a harbour area. Sensors 2015, 15, 1691–1707. [Google Scholar] [CrossRef] [PubMed]
- Young, I.; Rosenthal, W.; Ziemer, F. A three dimensional analysis of marine radar images for the determination of ocean wave directionality and surface currents. J. Geophys. Res. 1985, 90, 142–149. [Google Scholar] [CrossRef]
- Gangeskar, R. Ocean current estimated from X-band radar sea surface images. IEEE Trans. Geosci. Remote Sens. 2002, 40, 783–792. [Google Scholar] [CrossRef]
- Nieto-Borge, J.C.; Rodiguez, G.R.; Hessner, K. Inversion of marine radar images for surface wave analysis. J. Atmos. Ocean. Technol. 2004, 21, 1291–1301. [Google Scholar] [CrossRef]
- Nieto-Borge, J.C.; Hessner, K.; Jarabo-Amores, P.; MataMoya, D. Signal-to-noise ratio analysis to estimate ocean wave heights from X-band marine radar image time series. IET Radar Sonar Navig. 2008, 2, 35–41. [Google Scholar] [CrossRef]
- Liu, X.; Huang, W.; Gill, E.W. Wave height estimation from shipborne X-band nautical radar images. J. Sens. 2016, 2016, 1078053. [Google Scholar] [CrossRef]
- Wetzel, L.B. Electromagnetic scattering from the sea at low grazing angles. Surface Waves and Fluxes 1990, 8, 109–172. [Google Scholar]
- Buckley, J.R.; Aler, J. Enhancements in the determination of ocean surface wave height from grazing incidence microwave backscatter. In Proceedings of the 1998 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seattle, WA, USA, 6–10 July 1998. [Google Scholar]
- Gangeskar, R. Wave height derived by texture analysis of X-band radar sea surface images. In Proceedings of the IEEE 2000 International on Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 24–28 July 2000. [Google Scholar]
- Buckley, J.R. Can geometric optics fully describe radar images of the sea surface at grazing incidence? In Proceedings of the International Geoscience and Remote Sensing Symposium, Sydney, Australia, 9–13 July 2001. [Google Scholar]
- Plant, W.J.; Farquharson, G. Wave shadowing and modulation of microwave backscatter from the ocean. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Nieto-Borge, J.C.; Carro-Calvo, L.; Cuadra, L.; Hessner, K.; Alexandre, E. Significant wave height estimation using SVR algorithms and shadowing information from simulated and real measured X-band radar images of the sea surface. Ocean Eng. 2015, 101, 244–253. [Google Scholar] [CrossRef]
- Wijaya, A.P.; Van Groesen, E. Determination of the significant wave height from shadowing in synthetic radar images. Ocean Eng. 2016, 114, 204–215. [Google Scholar] [CrossRef]
- Liu, X.; Huang, W.; Gill, E.W. Comparison of wave height measurement algorithms for ship-borne X-band nautical radar. Can. J. Remote Sens. 2016, 42, 344–353. [Google Scholar] [CrossRef]
- Lu, Z.; Zhou, Y.; Huang, Y. Research on correlation in spatial domain to eliminate the co-channel interference of the X-band marine radar. Syst. Eng. Electron. 2017, 39, 758–767. [Google Scholar]
- Liu, Y.; Huang, W.; Gill, E.; Peters, D.; Vicen-Bueno, R. Comparison of algorithms for wind parameters extraction from shipborne X-band marine. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 896–906. [Google Scholar] [CrossRef]














| Radar Parameters | Value |
|---|---|
| Electromagnetic Wave Frequency | 9.3 GHz |
| Antenna height | 45 m |
| Antenna rotation speed | 22 r.p.m |
| Antenna Gain | 31 dB |
| Polarization | HH |
| Antenna length | 1.8 m |
| Horizontal Beam Width | 0.9 |
| Vertical Beam Width | 21 |
| Pulse Repetition Frequency | 1300 Hz |
| Pulse Width | 50 ns |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Lu, Z.; Pian, G.; Liu, H. Wave Height Estimation from Shadowing Based on the Acquired X-Band Marine Radar Images in Coastal Area. Remote Sens. 2017, 9, 859. https://doi.org/10.3390/rs9080859
Wei Y, Lu Z, Pian G, Liu H. Wave Height Estimation from Shadowing Based on the Acquired X-Band Marine Radar Images in Coastal Area. Remote Sensing. 2017; 9(8):859. https://doi.org/10.3390/rs9080859
Chicago/Turabian StyleWei, Yanbo, Zhizhong Lu, Gen Pian, and Hong Liu. 2017. "Wave Height Estimation from Shadowing Based on the Acquired X-Band Marine Radar Images in Coastal Area" Remote Sensing 9, no. 8: 859. https://doi.org/10.3390/rs9080859
APA StyleWei, Y., Lu, Z., Pian, G., & Liu, H. (2017). Wave Height Estimation from Shadowing Based on the Acquired X-Band Marine Radar Images in Coastal Area. Remote Sensing, 9(8), 859. https://doi.org/10.3390/rs9080859