A Study of Spatial Soil Moisture Estimation Using a Multiple Linear Regression Model and MODIS Land Surface Temperature Data Corrected by Conditional Merging

Abstract

This study attempts to estimate spatial soil moisture in South Korea (99,000 km²) from January 2013 to December 2015 using a multiple linear regression (MLR) model and the Terra moderate-resolution imaging spectroradiometer (MODIS) land surface temperature (LST) and normalized distribution vegetation index (NDVI) data. The MODIS NDVI was used to reflect vegetation variations. Observed precipitation was measured using the automatic weather stations (AWSs) of the Korea Meteorological Administration (KMA), and soil moisture data were recorded at 58 stations operated by various institutions. Prior to MLR analysis, satellite LST data were corrected by applying the conditional merging (CM) technique and observed LST data from 71 KMA stations. The coefficient of determination (R²) of the original LST and observed LST was 0.71, and the R² of corrected LST and observed LST was 0.95 for 3 selected LST stations. The R² values of all corrected LSTs were greater than 0.83 for total 71 LST stations. The regression coefficients of the MLR model were estimated seasonally considering the five-day antecedent precipitation. The p-values of all the regression coefficients were less than 0.05, and the R² values were between 0.28 and 0.67. The reason for R² values less than 0.5 is that the soil classification at each observation site was not completely accurate. Additionally, the observations at most of the soil moisture monitoring stations used in this study started in December 2014, and the soil moisture measurements did not stabilize. Notably, R² and root mean square error (RMSE) in winter were poor, as reflected by the many missing values, and uncertainty existed in observations due to freezing and mechanical errors in the soil. Thus, the prediction accuracy is low in winter due to the difficulty of establishing an appropriate regression model. Specifically, the estimated map of the soil moisture index (SMI) can be used to better understand the severity of droughts with the variability of soil moisture.

1. Introduction

Soil moisture (SM) is an important state variable governing the partitioning of rainfall into runoff and water that infiltrates the soil. Although the water contained in soil is only a tiny fraction of all the water on the Earth, it influences important extreme events, such as floods and droughts [1]. SM is existing soil water stored among soil particles and pores. Moreover, SM is a hydrometric factor that plays a crucial role in the exchange of water and energy in the land and atmosphere. Notably, SM has been studied in the agricultural field regarding plant growth, water resources field for rainfall-runoff, and meteorological field regarding interactions between the atmosphere and land [2].

There are multiple ways to estimate SM, including in situ networks and satellite remote sensing. Traditional in situ measurements provide valuable information on SM at different soil depths. Many field techniques are available, such as oven drying, neutron probe, time/frequency domain reflectometry (TDR/FDR), and capacitance measurements [3]. TDR, tension-measuring, and gravimetric methods are available to measure SM through ground observations. However, these methods are expensive and time consuming when used on large areas. Most allow point measurements, which provide information on the SM content at specific points only. In addition, reliability of the point data is also poor due to the short observation period as well as many missing data. Therefore, in situ SM is regarded as the true value of SM and is commonly used as a reference to validate remotely sensed SM retrieval [4,5,6]. However, in situ SM data of point scale are difficult to use as spatial SM [7,8,9] in large areas.

The estimation of spatial SM can be divided into direct measurement using microwave satellites and indirect measurement using land surface parameters related to SM without using microwave satellite data. First, microwave satellites are widely used because they allow the continuous observation of spatial SM over a wide area [10,11]. However, there are several limitations to directly and immediately using SM data based on satellites: (1) the relatively low spatiotemporal resolution of the data; (2) the only regional optimization algorithms for satellite soil moisture estimation are available from the National Aeronautics and Space Administration (NASA), European Space Agency (ESA), and Japan Aerospace Exploration Agency (JAXA); (3) the satellite data have not been calibrated and verified; and (4) radio interference. Nevertheless, many studies have been actively conducted to calibrate spatial SM based on satellite data compared to point-based observations of SM over wide areas [12,13,14]. For example, using the AMSR satellite, Kim et al. [15] obtained AMSR2 spatial SM data and performed a correction process using observed SM data. In addition, other studies have proposed microwave satellites SM downscaling method using MODIS and in situ data [16,17,18,19]. Second, spatial SM can be estimated from land surface parameters such as LST and NDVI without using microwave satellite data [20]. Moreover, LST has a unique relationship with spatial SM [21]. Examples of applications as non-microwave satellites using moderate resolution imaging spectroradiometer (MODIS) LST data are as follows. Cai et al. [22] obtained SM retrieval form Terra MODIS L1B data. Kim et al. [23] improved the spatial SM of AMSE-E through the integration of MODIS land surface temperature (LST), the enhanced vegetation index (EVI) and albedo. MODIS data have been successfully used to increase the accuracy of spatial SM estimates.

Although MODIS LST has been used in various ways, MODIS LST should be regenerated using gap-filling and correction processes, which can convert global data to region data. Notably, daily MODIS LST datasets (MOD11_L2) have missing values due to clouds and atmospheric conditions [24]. In some previous studies, MODIS LST was corrected by spatial interpolation and geostatistical methods [24,25]. To overcome this issue, geostatistical methods (e.g., kriging, inverse distance weighting and spline methods) can be applied to ground measurements by matching the spatial scale with satellite-based products [26,27]. In rainfall research, various strategies for combining satellite-based and observed data have been widely used to overcome the limitation of areal representativeness of point scale measurements and the high variability in satellite-based datasets. This method, which is called “conditional merging (CM)” in Sinclari et al. [28], uses the radar field to estimate the error associated with the ordinary kriging method based on rain gauges and to correct it [29]. In general, previous studies that have used the CM method yielded reasonable results compared to ground-based measurements and exhibited improved spatial and temporal variability [30].

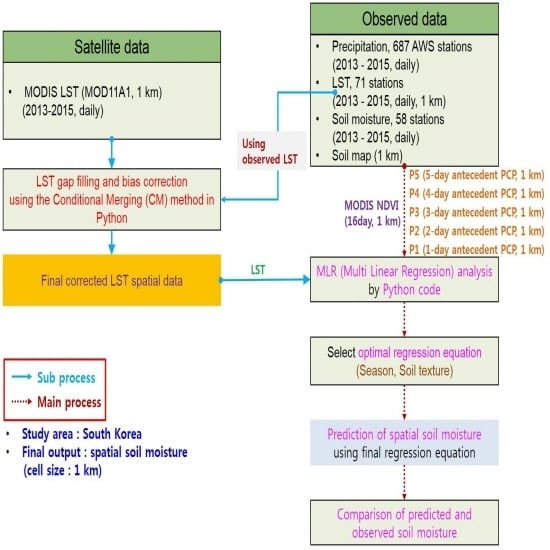
The overall goal of this study was to estimate spatial SM based on MODIS LST and normalized difference vegetation index (NDVI) data via multiple linear regression (MLR) analysis (Figure 1). The specific objectives of the study were as follows: (1) to correct MODIS LST using the CM method; (2) to develop the MLR model using corrected MODIS LST, MODIS NDVI data, and interpolated precipitation (PCP); (3) to generate the spatial distribution of SM using normalized regression coefficients; (4) to assess spatial SM estimates and (5) to compare the SM index (SMI) and standardized precipitation index (SPI) to evaluate the usability of spatial SM.

2. Materials and Methods

The study analyzed SM based on satellite data via correlation analysis. Principle component analysis was used to effectively select independent variables among the environmental attributes of SM. Finally, MLR model was developed using MODIS LST, MODIS NDVI, and PCP from various regression scenarios. In this study, various satellite data and observed point data were used with 1 km spatial resolution (

Table 1. Description of data specifications.

Data	Temporal Resolution	Spatial Resolution	Reference Resolution	Duration	Note
MODIS land surface temperature (LST)	Daily	1 km	1 km	2013–2015	Satellite data
MODIS normalized difference vegetation index (NDVI)	16 day	500 m	1 km	2013–2015	Satellite data
Precipitation	Daily	687 stations	1 km	2013–2015	Point data
Soil moisture	Daily	58 stations	1 km	2013–2015	Point data
Observed LST	Daily	71 stations	1 km	2013–2015	Point data
Soil map		1 km	1 km		Investigated data

). The soil map data (soil type, field capacity, and wilting point) obtained from the Korea Rural Development Administration (KRDA) were rasterized from a 1/25,000 vector map.

2.1. Satellite Data

The LST is a key variable used in a wide range for monitoring of surface radiation budget, climate change, hydrological cycle and ecosystems. In spite of the recognized importance of LST, observed LST on land are not yet adequate for assessing diurnal cycles or analyzing seasonal and inter-annual variability because of large spatiotemporal variations. MODIS LST (MOD11A1) and MODIS NDVI (MOD13Q1) were used as satellite datasets in this study. The MODIS land products include the energy balance product, vegetation parameter product, and land cover/land use product (http://modis-land.gsfc.nasa.gov/). These products have been widely applied in global and regional monitoring, modeling and assessment.

2.1.1. MODIS LST

MODIS LST is estimated using a statistical regression-based method based on 12 MODIS thermal infrared (TIR) bands, with an option for non-linear physical retrieval. The regression coefficients of the statistical retrieval are derived using a fast radiative transfer model with atmospheric characteristics taken from a dataset of 12,208 global profiles of atmospheric temperature, moisture, and ozone [31]. Notably, the accuracy of the product may be affected by errors in land surface emissivity (Eva Borbas, personal communication). The MODIS LST (MOD11) product is retrieved using the generalized split-window algorithm [32,33]:

$$\begin{array}{r}{T}_s = \mathrm{C} + \left(A_1 + A_2\frac{1-\epsilon }{\epsilon } + A_3\frac{\Delta \epsilon }{{\epsilon }^2}\right) \times \frac{T_{31}+T_{32}}{2}\\ + \left(B_1+B_2\frac{1-\epsilon }{\epsilon }+B_3\frac{\Delta \epsilon }{{\epsilon }^2}\right) \times \frac{T_{31}-T_{32}}{2}\end{array}$$

(1)

$$\mathsf{\epsilon } =\left({\epsilon }_{31} + {\epsilon }_{32})/2\right)$$

(2)

$$\Delta \epsilon = {\epsilon }_{31} - {\epsilon }_{32}$$

(3)

where $T_s$ is LST, $T_{31}$ and $T_{32}$ are brightness temperatures in MODIS bands 31 and 32, respectively, ${\epsilon }_{31}$ and ${\epsilon }_{32}$ are surface emissivities in MODIS bands 31 and 32, respectively, and $\mathrm{C},A_1,A_2,A_3, B_1,B_2$, and $B_3$ are regression coefficients [34]. MOD11A1 data are daily level-3 global LST products gridded in the Sinusoidal projection (version 4) at spatial resolution of 1 km and collected twice per day using the generalized split-window algorithm [33,35,36].

2.1.2. MODIS NDVI

The MODIS sensors onboard the Terra satellite acquire data in 36 discrete spectral channels with a spatial resolution of 250 m for the visible bands, 500 m for the near-infrared bands, and 1000 m for the remaining thermal infrared bands (http://modis.gsfc.nasa.gov/). To obtain the MODIS NDVI data among the products, the MODIS 500-m NDVI 16-day composite scenes (MOD13Q1) from January 2013 to May 2015 were retrieved from the Land Processes Distributed Active Archive Center (LP DAAC, https://lpdaac.usgs.gov/).

NDVI is a distributed vegetation condition index based on differences in the reflectivity of near infrared light. The NDVI reflects the presence of vegetation on a pixel basis and provides measures of the amount and condition of vegetation within a pixel [31]. NDVI values were calculated using Equation (4) in each grid cell:

$$\mathrm{NDVI} =\frac{NIR - RED}{NIR + RED}$$

(4)

where NIR is the near infrared band (MODIS band 2), and RED is the red band (MODIS band 1). In this study, MODIS NDVI composited to 16 days was resampled from UTM format and a 500 m resolution to the WGS84 projection and a 1 km spatial resolution for the MODIS LST reference.

2.2. Observed Data

2.2.1. Automatic Weather Stations (AWSs)

The Korea Meteorological Administration (KMA) operates the AWSs, which include 687 stations throughout South Korea, to continuously monitor weather conditions (Figure 2a). The average distance between stations is approximately 13 km, and the raw data are collected in 10 min intervals. The data set used in this study is archived at 24 h intervals.

In this study, we used 687 AWS precipitation data points during the simulation period. First, we obtained minute-scale precipitation data from KMA and compared it with the operation period data. Second, minute-scale precipitation data were converted into daily data, and the data were interpolated using the inverse distance weighting (IDW) method based on the 1-km spatial resolution of the MODIS LST reference.

2.2.2. Soil Moisture and Soil Data of the Stations

To develop a model for expected SM, the regression model requires observed SM data from various stations. This study used SM data measured by KMA at 9 stations, the Hydrological Survey Center (HSC) at two stations, K-water (Korea Water Resources Corporation) at 7 stations and the Rural Development Administration (RDA) at 40 stations (

Table 2. Agrometeorological observation network of the Korea Meteorological Administration and the other observation points with soil type.

No.	Station	Latitude	Longitude	Soil	No.	Station	Latitude	Longitude	Soil
1	CW	38.20	127.25	Sand	30	MM	36.01	127.68	Loam
2	SW	37.27	126.99	Sand	31	NI	35.43	127.44	Loam
3	SC1	35.07	127.24	Sand	32	JJ4	35.62	127.51	Clay
4	CJ	36.64	127.44	Sand	33	JJ5	35.62	126.90	Clay
5	CC1	37.90	127.74	Loam	34	YG2	35.28	126.47	Clay
6	SS1	36.77	126.50	Loam	35	GO	35.27	127.30	Loam
7	BS	34.76	127.21	Loam	36	HH4	34.97	127.07	Clay
8	CC2	35.68	127.51	Loam	37	HH5	35.05	126.54	Clay
9	GB1	35.81	127.63	Silt	38	YD	34.83	126.67	Clay
10	JC1	35.97	127.42	Loam	39	HS	34.53	126.56	Clay
11	HB	37.22	126.95	Loam	40	HU	34.58	126.65	Clay
12	YC	37.17	127.30	Loam	41	JG	34.51	126.30	Clay
13	IJ	37.27	127.43	Silt	42	BU	34.76	127.09	Silt
14	YY1	37.51	127.51	Loam	43	YJ	34.79	127.65	Clay
15	HH1	38.11	127.69	Clay	44	GJ	35.82	128.81	Clay
16	PU	37.54	128.45	Loam	45	CY	36.04	128.38	Clay
17	HH2	37.71	127.86	Loam	46	SD2	35.91	128.25	Loam
18	II	38.06	128.17	Loam	47	SC2	36.45	128.17	Clay
19	CH	36.62	127.42	Loam	48	YY3	36.85	128.56	Silt
20	CO	36.72	127.46	Clay	49	CC4	36.39	129.08	Sand
21	YS2	36.21	127.72	Silt	50	YO	35.99	128.93	Clay
22	JB	37.16	128.18	Sand	51	PB	36.11	129.31	Loam
23	NG	36.21	127.14	Clay	52	GG4	34.99	128.33	Silt
24	GD	36.20	127.28	Loam	53	TG2	34.90	128.40	Silt
25	YS3	36.74	126.81	Silt	54	JC2	35.20	128.12	Clay
26	CC3	36.43	126.78	Loam	55	SY	35.04	128.07	Clay
27	HH3	36.59	126.64	Clay	56	HJ	35.13	128.28	Clay
28	JJ3	35.76	127.44	Loam	57	GG5	35.68	127.92	Loam
29	GB2	35.75	126.85	Clay	58	HH6	35.55	128.11	Sand

and Figure 2b). The automated agriculture observing system (AAOS) operated by KMA provides observations of weather phenomena that are closely related to agriculture at 10 auxiliary agricultural weather observatories located throughout the country, including the Suwon (SW) meteorological observatory, which is a basic agricultural meteorological observation office according to the technical regulations of the World Meteorological Organization (WMO). In this study, SM data at 10 cm of depth were collected at 9 sites (the Seogwipo and Andong sites did not provide good SM data and were not used. The technical specifications of the KMA data were previously reported [37]. Stations No. 10 to No. 12 are flux towers. Nos. 10 and 11 are within the Han River basin, the largest river basin in South Korea (total area of 34,406 km²), and are operated by HSC, and No. 12, which is operated by K-water, is located in the Geum River basin at an elevation of 688.568 m and a height of 25 m to avoid the effects of the reservoir and canopy. Nos. 13 to 18 are installed in the Yongdam Dam watershed in the Geum River basin and are operated by K-water. These data were measured using time domain reflectometry (TDR) at an average depth of 10 cm. The data are provided by the Yongdam Experimental Catchment (http://www.ydew.or.kr/kdrum/main/main.do). The observed stations from No. 19 to the end of the list are operated by RDA and utilize TDR. These data were provided by the Agricultural Meteorology Information Service (http://weather.rda.go.kr). All SM data were prepared from January 2013 to December 2015, but some data, especially RDA data, were prepared for a limited period of the time because of the short observation period.

2.3. Conditional Merging (CM) Technique

The CM technique [38,39,40] is a method of spatial interpolation suited for merging spatially continuous grid-based measurements and point measurements. The method has the advantage of precisely preserving the spatial covariance structure of spatially continuous grid-based measurements while maintaining the accuracy of the point-based measurements. The algorithm has been applied and showed superior performance to the traditional geostatistical approaches, especially in obtaining spatial rainfall fields in several regions across the world [29,30,40,41,42]. The CM technique is also known as the kriging error correction technique based on radar-based or satellite-based data. Geostatistical merging methods such as mean field bias correction (MFB), range-dependent adjustment (RDA), Brande spatial adjustment (BRA), ordinary kriging (KRI), kriging with external drift (KED), and CM technique have been tried. Goudenhoofdt et al. [29] performed and evaluated various methods for combining spatial and gauge data. They found that the CM and KED techniques provided the best methods of improving the spatial interpolation of gauges values. Therefore, CM technique was selected among various methods in this study.

In this study, the CM technique includes the following six processes: (a) observed LST are collected at 71 stations of KMA; (b) LST values measured at the 71 stations are interpolated using the ordinary kriging technique with 1 km spatial resolution of the MODIS LST reference; (c) satellite LST data are collected with 1 km spatial resolution; (d) the satellite LST at the 71 gauging stations are extracted and then spatially interpolated using the ordinary kriging technique with 1 km spatial resolution of the MODIS LST reference; (e) the residual between (c) and (d) is calculated; and (f) the residual values of (e) are added to the data from (b) to produce the final satellite-observed composite LST dataset with 1 km spatial resolution (Figure 3).

2.4. Multiple Linear Regression Model and Scenarios

Regression analysis is commonly used to measure the relationship between two or more variables, predicting the behavior of a dependent or endogenous variable according to one or more independent or explanatory variables. Multiple linear regression (MLR) models are frequently used as empirical models or approximating functions and to establish a mathematical model to describe a real-world phenomenon. Generally, the relationship between the dependent and the independent variables is given as presented as in Equation (5) [43].

$$\mathrm{Y} = \mathrm{C} + {\beta }_1{X}_1 + {\beta }_2{X}_2 + {\beta }_3{X}_3 + {\beta }_4{X}_4 +\dots + {\beta }_n{X}_n$$

(5)

where Y is the dependent variable, $\mathrm{C}$ is a constant, $X_1, X_2, X_3, X_4 and X_n$ are independent variables, and ${\beta }_1, {\beta }_2, {\beta }_3,{\beta }_4 \mathrm{and} {\beta }_n$ are regression coefficients.

From input data, including MODIS LST, MODIS NDVI, PCP_n, PCP_n-1, PCP_n-2, PCP_n-3, PCP_n-4 and PCP_n-5, were used to develop the model. Notably, PCP_n is the precipitation on the observation day. PCP_n-5, PCP_n-4, PCP_n-3, PCP_n-2, and PCP_n-1 indicate antecedent precipitation from five days to one day (

Table 3. Eight regression scenarios for MLR model using MODIS LST, MODIS NDVI, precipitation of the observation day (PCP_n), one day antecedent precipitation (PCP_n-1), two-day antecedent precipitation (PCP_n-2), three-day antecedent precipitation (PCP_n-3), four-day antecedent precipitation (PCP_n-4), and five-day antecedent precipitation (PCP_n-5).

Scenario	LST	NDVI	PCP (mm)
			n	n-1	n-2	n-3	n-4	n-5
1	○		○
2		○	○
3	○	○	○
4	○	○	○	○
5	○	○	○	○	○
6	○	○	○	○	○	○
7	○	○	○	○	○	○	○
8	○	○	○	○	○	○	○	○

Note: ○ denotes an independent variable used in the regression scenario.

).

2.5. Seasonal Analysis and Normalization of the Regression Coefficients

In a previous study [44], several input datasets were selected, such as LST, NDVI, sunshine hours and precipitation, and twelve scenarios were developed according to the combinations of input data. In addition, the correlation increased when the model coefficients were evaluated on a seasonal basis due to the reverse correlation between MODIS NDVI and SM in spring and autumn. Therefore, the MLR regression coefficients were calculated by seasonal analysis.

In general, statistical analysis and normalization should be performed to reduce uncertainty in MLR models. The disadvantage of unnormalized regression is that the independent variables usually have different units. Thus, it is difficult to compare the relative influence of each independent variable on the dependent variable. The unnormalized regression coefficient is dependent on the measurement scale, while the normalized regression coefficient is not. Normalization typically shows which independent variable has the largest influence on the dependent variable in MLR analysis. In this study, the normalization was performed using the min–max normalization expression given in Equation (6) [45].

$$\mathrm{Normalization} = \frac{\left(Independent variable-Minmum Independent variable\right)}{\left(Maximum Independent variable-Minimum Independent variable\right)}$$

(6)

2.6. Soil Moisture Index (SMI)

Spatially distributed SM is often used in spatial drought indices. The SM-based drought index, known as the SMI, provides the severity and duration of an agricultural drought for an area of interest. Available water for plants is defined as the quantity of soil water between field capacity (FC) and the lower limit of extractable water, which is known as the wilting point (WP), and this stored water is extracted by plant roots [46]. Available water is therefore an important metric for quantifying agricultural droughts if it is converted into an index. In this study, available water is first calculated based on the observed or modeled SM that is normalized by the maximum available water for plants, calculated as the difference between the field capacity and wilting point, to derive the SMI. This index is classified from no drought to extreme drought to quantitatively assess droughts in space and time [47]. In general, the SMI reflects the level of agricultural drought. However, SMI has not yet been evaluated as an authorized drought index in South Korea by lack of spatial confidence. Therefore, this study additionally examined the efficiency of spatial SMI compared to the standardized precipitation index (SPI), which is widely used as a meteorological drought index. In South Korea, the SPI distribution is provided by the Drought Information System (http://drought.kma.go.kr) of the KMA.

The SMI is computed based on the soil characteristics and SM conditions, and the parameters include FC, WP and SM. The soil map data (FC, WP and soil type) were obtained from the KRDA (Figure 4). Then, the soil map was rasterized at a 1 km spatial resolution. We used these data to estimate the SMI. The dominant soils are sand (31.2%) and loam (38.8%). The FC ranges from 9% to 40%, and the average FC of all regions is 22.1%. Additionally, the WP ranges from 3% to 15%, with an average WP of 5.6% in all regions. The SMI equation is given as follows.

$$\mathrm{SMI} = \left[\frac{5 \times \left(SM-WP\right)}{\left(FC - WP\right)} - 5\right]$$

(7)

This equation yields SMI values ranging from less than −5 to 0. Thus, the actual SM in the soil column is normalized based on the available water content (AWC) in the soil column. This normalized value then used to compute the index. The range is chosen via a method similar to that of the U.S. Drought Monitor to maintain consistency and compare the drought severity. An SMI of 0 indicates no drought, but conditions could be heading toward drought or moving out of a drought. An SMI of −1 reflects a low-intensity drought, while an SMI of −5 reflects an extreme drought [47].

3. Results and Discussion

3.1. Corrected MODIS LST Data

The leave-one-out cross-validation method was used to assess the performance of the CM technique in predicting the LST values at ungauged locations. In this technique, observed LST stations are assumed to be nonexistent at given gauge locations, and a spatial interpolation technique (CM) is applied to obtain the values at these points. Then, the estimated values obtained from the CM technique are compared to the original values at all measurement locations. All observed daily LST data measured by 71 stations of KMA from January 2013 to December 2015 (Figure 5).

For verifying LST by CM, some LST stations were assumed to be ungauged stations for verifying LST in green ellipses of Figure 5. LST stations used for verification considered three conditions: (1) the locations in coastal and inland regions; (2) the proximity of the SM observation station; and (3) each land use. From that, 129, 192 and 238 stations are selected by coastal and agricultural area (129), coastal and pasture area (192), and inland and forest area (238) for verifying LST.

After excluding three stations, the CM technique was applied to calculate the corrected LST distribution. The coefficient of determination (R²) values were high at all stations, including verified stations, and varied from 0.89 to 0.99. Overall, the calibration results at the three points excluded from the CM process showed good results between observed and simulated values (Figure 6). Finally, monthly spatial distribution map of corrected LST was generated by the CM technique from 2013 to 2015. Figure 7 shows monthly spatial distribution maps of corrected LST from April to September in drought years (2013–2015).

3.2. Optimal Regression Equation and Regression Coefficients

To determine the optimal regression scenario, the regression coefficients of MLR equations were assessed (

Table 4. Regression coefficients of multiple linear regression for each scenario.

Scenario	Constant	Corrected LST	Original LST	NDVI	PCP (mm)						R2
					N	n-1	n-2	n-3	n-4	n-5
1	18.950	0.441			0.126						0.24
2	33.427			−14.955	0.155						0.22
3	29.526	0.604		−23.512	0.124						0.30
4	29.265	0.610		−3.842	0.100	0.174					0.35
5	29.163	0.610		−24.145	0.110	0.153	0.134				0.37
6	29.065	0.609		−24.397	0.118	0.159	0.117	0.125			0.40
7	28.946	0.608		−24.608	0.117	0.168	0.123	0.108	0.111		0.43
8	22.484	0.585		−25.071	0.099	0.142	0.113	0.091	0.080	0.086	0.45
9	23.942		0.082	−5.465	0.140	0.182	0.142	0.126	0.090	0.099	0.39

). Moreover, scenario 9 was additionally added to assess how the result of corrected MODIS LST would be affected in R². In the correlation analysis, R² was used to assess the results. The weighted effect of each regression coefficient on SM is given in Table 4. Scenario 1 only used MODIS LST and PCP_n to estimate SM, and the resulting R² was 0.22. However, R² increased to 0.24 and 0.45 when LST, PCP_n, PCP_n-1, PCP_n-2, PCP_n-3, PCP_n-4, and PCP_n-5 were included. From this result, Scenario 8, which included nine independent variables, was selected as the optimal regression equation. Additionally, the R² of Scenario 9 decreased by 0.06 when original MODIS LST was applied, compared with the result of Scenario 8.

From an optimal regression equation, the regression coefficients of the MLR model were re-estimated based on the four soil classes (clay, loam, sand, silt) and four seasons (spring, summer, autumn, winter) considering the antecedent precipitation for up to five days. The regression coefficients of optimal scenario were divided into 16 regression coefficients over four seasons and four soil types (

Table 5. Regression coefficients in four seasons and for four soil types.

Soil Type	Season	Con.	LST	NDVI	PCP (mm)						R2
					n	n-1	n-2	n-3	n-4	n-5
Silt	Spring	23.698	−0.109	−0.045	0.103	0.155	0.110	0.088	0.080	0.104	0.44
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Summer	25.503	−0.314	6.693	0.052	0.068	0.045	0.037	0.024	0.028	0.38
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Autumn	21.111	−0.190	6.963	0.120	0.152	0.106	0.090	0.076	0.072	0.29
		(0.000)	(0.000)	(0.080)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Winter	20.514	0.829	1.374	0.091	0.206	0.242	0.171	0.162	0.176	0.29
		(0.000)	(0.000)	(0.060)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Clay	Spring	31.684	0.170	−31.417	0.038	0.067	0.035	0.030	0.031	0.021	0.67
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Summer	14.239	0.770	−20.071	0.021	0.024	−0.002	−0.002	0.016	0.003	0.60
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Autumn	31.562	0.685	−37.067	0.048	0.073	0.055	0.047	0.031	0.021	0.57
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Winter	29.505	0.510	−20.468	−0.050	0.059	0.038	0.008	0.008	0.020	0.40
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Loam	Spring	28.995	−0.152	−8.580	0.127	0.174	0.143	0.124	0.110	0.116	0.45
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Summer	18.458	−0.145	6.881	0.096	0.110	0.093	0.081	0.073	0.079	0.53
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Autumn	23.911	−0.159	−1.427	0.163	0.210	0.164	0.143	0.133	0.127	0.39
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Winter	22.260	0.211	6.528	0.237	0.300	0.272	0.224	0.197	0.227	0.28
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Sand	Spring	19.595	−0.170	0.830	0.113	0.165	0.108	0.091	0.076	0.103	0.42
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Summer	13.837	−0.117	9.896	0.070	0.076	0.053	0.047	0.037	0.040	0.36
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Autumn	21.085	−0.288	3.611	0.112	0.126	0.086	0.062	0.053	0.050	0.44
		(0.000)	(0.036)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	Winter	13.794	0.477	9.598	0.244	0.308	0.267	0.211	0.170	0.188	0.29
		(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)

Note: () indicates p-value. Within a column at each scale, means followed by the same letter are not significantly different (p-value < 0.05). R² is the coefficient of determination.

). Each regression coefficient was presented with the p-value to confirm the statistical significance, and the coefficient of determination (R²) was used for correlation analysis. Overall, the p-values of all the regression coefficients were less than 0.05, except for the autumn and winter regression coefficients of NDVI for silt, indicating statistical significance. The reason for the high p-values of the regression coefficients of NDVI for silt in autumn and winter is that most of the observations corresponding to silt are provided by the RDA and the data are insufficient (data were available for a period of less than a year).

The MLR coefficients showed that R² increased from 0.07 to 0.24 when we estimated the coefficient seasonally compared with the coefficients that were not estimated seasonally (0.22 to 0.43). These results indicate that the correlation between observed soil moisture and estimated SM was improved by considering seasonal and soil type patterns. Nevertheless, the reason for the low R² of less than 0.5 was that the soil classification for each observation site was not complete. It was difficult to classify the soil classes of the RDA’s stations (from No. 19 to 58) because these stations were not stabilized; the stations have only been measuring SM since December 2014. In addition, the classification of 12 soil types into four soil types also contributed to the poor accuracy. Therefore, if we add more soil moisture observations or extend the observation period and refine the soil classification to more than four soil types, the simulation results would improve.

The seasonal regression coefficients showed the highest correlation in all four soil classes in spring and summer. Because of the characteristics of the monsoon climate in South Korea, where precipitation is concentrated in summer, there are many values that are effective for regression analysis based on antecedent precipitation, and it is estimated that the correlation is high. However, the reason for the low R² of the four soil types in winter is that SM data in winter are associated with high uncertainty because the soil is frozen, which can cause instrument errors.

3.3. Soil Moisture by Regression Coefficients of Optimal Scenario

Using the optimal scenario, the accuracy of SM estimation was evaluated via comparison to observed SM at 58 stations. SM was estimated using the regression coefficients, and the accuracy with respect to the observed SM was verified by R² and root mean square error (RMSE) (

Table 6. Summary of the average (2013–2015) R² and root mean square error (RMSE) values at 58 soil moisture stations.

Station	R2	RMSE (%)	Station	R2	RMSE (%)	Station	R2	RMSE (%)
1	0.54	2.02	21	0.61	1.63	41	0.53	5.22
2	0.36	9.64	22	0.68	1.09	42	0.39	2.17
3	0.39	12.21	23	0.55	3.32	43	0.55	2.48
4	0.35	2.88	24	0.35	4.06	44	0.39	3.65
5	0.48	1.61	25	0.35	1.25	45	0.60	1.14
6	0.34	3.21	26	0.34	0.56	46	0.60	2.09
7	0.39	2.93	27	0.31	4.16	47	0.44	0.46
8	0.48	1.62	28	0.52	3.57	48	0.50	3.75
9	0.38	2.53	29	0.59	4.62	49	0.42	2.41
10	0.76	0.82	30	0.34	2.55	50	0.51	0.86
11	0.43	3.56	31	0.50	3.74	51	0.40	2.51
12	0.52	1.91	32	0.33	1.77	52	0.47	1.42
13	0.41	1.68	33	0.53	5.91	53	0.36	3.80
14	0.32	2.44	34	0.47	1.42	54	0.32	2.00
15	0.52	3.80	35	0.60	2.04	55	0.43	2.39
16	0.42	3.10	36	0.61	1.55	56	0.45	0.46
17	0.59	2.59	37	0.60	1.05	57	0.54	5.22
18	0.68	2.31	38	0.60	0.76	58	0.35	2.55
19	0.41	0.71	39	0.30	4.31
20	0.68	1.26	40	0.55	1.86

). The graphs between observed SM and estimated SM at major stations are illustrated in Figure 8.

R² and RMSE for all soil types ranged from 0.30 to 0.76 (R²) and 0.46% to 12.21% (RMSE). The overall R² and RMSE were greater than 0.4 (R²), indicating a constant correlation. Most of the RMSEs were less than 5.0% (RMSE), but the RMSEs at Stations 1 and 2 were greater than 9.0% (RMSE). The main errors may have been associated with the artificial water supply. Unlike other stations, these two stations are located near upland crop and paddy field areas. Therefore, the observed SM was likely influenced by the agricultural water supply in addition to precipitation during the irrigation period from April to June.

Notably, R² and RMSE in winter were poor, as illustrated by the many missing values, and uncertainty exists in observations due to freezing and mechanical errors in the soil. Thus, the prediction accuracy is low in winter due to the difficulty of establishing an appropriate regression model. Additionally, some observations with low correlations did not fit the soil properties. After refining the soil classes in further research, it is expected that the R² and RMSE of these observatories, as well as those of the other observation sites, will increase because of the characteristics of the regression model. Currently, 43 of the 58 stations are occupied by loam and clay, and these 43 stations are calculated using one regression equation for each season. Therefore, as mentioned above, improvement of the soil classification is necessary.

3.4. Distribution of Estimated Soil Moisture

The SM distribution by soil type was estimated using normalized regression coefficients (

Table 7. Normalized regression coefficients in four seasons and for four soil types.

Soil Type	Season	Con.	LST	NDVI	PCP (mm)
					n	n-1	n-2	n-3	n-4	n-5
Silt	Spring	0.426	−0.082	−0.040	0.565	0.825	0.584	0.463	0.426	0.297
	Summer	0.472	−0.170	0.003	0.266	0.321	0.193	0.151	0.103	0.123
	Autumn	0.322	−0.030	−0.037	0.535	0.652	0.463	0.405	0.351	0.330
	Winter	0.030	0.757	−0.022	0.024	0.187	0.249	0.157	0.135	0.145
Clay	Spring	0.632	0.411	−0.719	0.129	0.142	0.128	0.087	0.091	0.125
	Summer	0.635	0.509	−0.627	0.329	0.250	0.218	0.210	0.212	0.169
	Autumn	0.307	1.499	−1.156	0.054	0.183	0.082	0.126	0.049	−0.045
	Winter	−0.089	0.846	−0.069	0.205	0.376	0.302	0.230	0.223	0.144
Loam	Spring	0.621	−0.224	−0.065	0.327	0.454	0.375	0.318	0.275	0.280
	Summer	0.329	−0.110	0.116	0.424	0.473	0.415	0.358	0.325	0.355
	Autumn	0.657	−0.383	0.083	0.334	0.448	0.343	0.300	0.283	0.271
	Winter	0.382	0.146	0.119	0.210	0.263	0.233	0.198	0.174	0.195
Sand	Spring	0.469	−0.271	0.006	0.222	0.323	0.214	0.182	0.148	0.205
	Summer	0.248	−0.080	0.164	0.240	0.260	0.183	0.163	0.128	0.138
	Autumn	0.499	−0.372	0.033	0.331	0.368	0.253	0.186	0.162	0.152
	Winter	0.137	0.357	0.173	0.316	0.401	0.353	0.275	0.224	0.247

Note: Standardization was performed for each independent variable. The equation is given as follows: Standardization = (Variable (constant, LST, NDVI, PCP_n) − Minimum variable (constant, LST, NDVI, PCP_n)/Maximum variable (constant, LST, NDVI, PCP_n) − Minimum variable (constant, LST, NDVI, PCP_n)).

). The monthly distribution maps of spatial SM and spatial precipitation (PCP) were generated from 2013 to 2015 (Figure 9). From the results of the monthly distribution map, spring drought was severe until March due to the absence of rain in 2013 and 2015. As seen from Figure 9, there was no rainfall in other regions, except for northeastern South Korea, until January. Therefore, SM was relatively low compared with other regions. Because PCP was observed throughout South Korea from March to April, SM increased by 5–6%. However, SM in May decreased due to the absence of rain. These results show that SM depends on spatial PCP pattern.

In particular, in the June SM map, the SM in the western part of the Korean Peninsula sharply decreased because there was no rainfall for the three months after March from 2013 to 2015. This trend is due to the monsoon climate of the area. All areas of South Korea are affected by monsoons, and wet and dry seasons occur each year, with seasonal variations in precipitation. Usually, June through August (summer) is the wet season, and most of yearly rainfall occurs during this period. Approximately 30% of the annual rainfall occurs in the other 9 months.

3.5. Comparison of Drought Index

The SMI and SPI in 2015, an extreme drought year, are illustrated in Figure 10. The SPI was extremely low (dry) in Gyeonggi and Gangwon Provinces (northern part of South Korea) on 1 January 2015. In March and May, SMI and SPI values show that drought was alleviated by rain. However, the SMI and SPI levels remained severe in Gyeonggi and Gangwon Provinces. This drought was resolved by large-scale rainfall events in July, and the SMI approached zero in southern regions where rainfall occurred. After July, the soil moisture naturally increased and decreased according to the precipitation. This pattern is consistent with the tendency of SPI. Coupling with SPI, SMI can be used as meteorological drought index in forested area and agricultural drought index in cultivation area.

4. Conclusions

This study estimated the spatial SM of South Korea from January 2013 to December 2015 using an MLR model and MODIS satellite data and evaluated the results by comparison with observed SM data at 58 stations. From the original MODIS LST data, daily spatial LST was corrected using CM technique. Additional satellite data (NDVI of Terra MODIS) were used to reflect vegetation variation. The observed precipitation measured from AWSs of the KMA considered during the simulation period was interpolated using the IDW method to match the spatial resolution of 1 km. Although the USDA textural classification, which divides soil into 12 classes, is one of the most widely used soil classification systems, the soil was classified into four types (loam, sand, clay and silt) based on the largest proportion of soil in South Korea. Finally, the regression coefficients of the MLR model were estimated seasonally considering the five-day antecedent precipitation. The primary results are summarized as follows:

• The R² of MODIS LST corrected by CM were between 0.83 and 0.99 at all LST stations. The results showed the values were generally accurate compared to the observed LST.
• The p-values of all the regression coefficients were less than 0.05, except for a few coefficients of NDVI for silt, indicating statistical significance. The R² values of the regression coefficients for the 4 soil classes were between 0.28 and 0.67. The reason for the low R² values of less than 0.5 is that the soil classification for each observation site was not completely accurate.
• The seasonal regression coefficients showed the highest correlation in all four soil classes in summer due to the characteristics of the monsoon climate in South Korea, where precipitation is concentrated in summer. There are many values that are effective for regression analysis based on antecedent precipitation.
• When we simulated SM using the estimated regression coefficients, the overall R² was greater than 0.4 at most observation sites (approximately 66%), except for some observations. Therefore, as mentioned above, improvements in soil and season classification are necessary.
• For distributing spatial SM, normalized regression coefficients were estimated using min–max normalization. Normalization typically showed relationship which independent variable has the largest influence on the dependent variable in MLR analysis. In this study, the normalization was performed using min–max normalization.
• In the spatial soil moisture distribution, simulated SM tends to increase and decrease with precipitation. This tendency is more clearly seen in the SMI map, where the SMI decreases from −2 to −3, indicating a weak drought. From March to April in 2014, PCP was observed throughout South Korea. Thus, SM also increased by 5–6%. These results showed that approximately 60% of the drought areas predicted by the SMI and SPI overlapped.

The result of the CM technique in this study showed that the accuracy of MODIS LST data improved by 20–30%. In regression analysis, the most important variables for estimating SM include 2-day, 3-day, 4-day and 5-day antecedent precipitation, LST and NDVI. SM exhibits spatially different patterns, even in areas with the same land use and soil characteristics. Overall, this study develops a high-resolution and accurate spatial distribution of SM for the first time based on satellite data. The results of this study showed that spatial resolution improved by 90% (10 km to 1 km) and R² increased by 62% (0.30 to 0.49) compared with the spatial resolution (10 km) and R² (0.30) of a previous study [48] based on AMSR2 satellite data. Although machine learning methods such as MLR and artificial neural network (ANN) may achieve better accuracy, there are still some limitations. The MLR model is trained with a large number of samples, and the more training samples that are available, the better the model fits the data. This fact draws on a requirement for the abundance of historical satellite data and contemporary in situ SM observations. If the satellite data and in situ SM archive is not abundant enough, then the relation values cannot be fully represented by historical observation pairs [49]. Notably, this study is the first to spatially estimate SM using MODIS LST corrected using the CM technique in South Korea. Therefore, this study provides a framework for accurate SM prediction in ungauged areas. Future research study could be improved if the soil classification is further subdivided and the soil moisture regression coefficient is simulated based on more observed data.